2008年中考数学分类真理练习19三角函数 26页

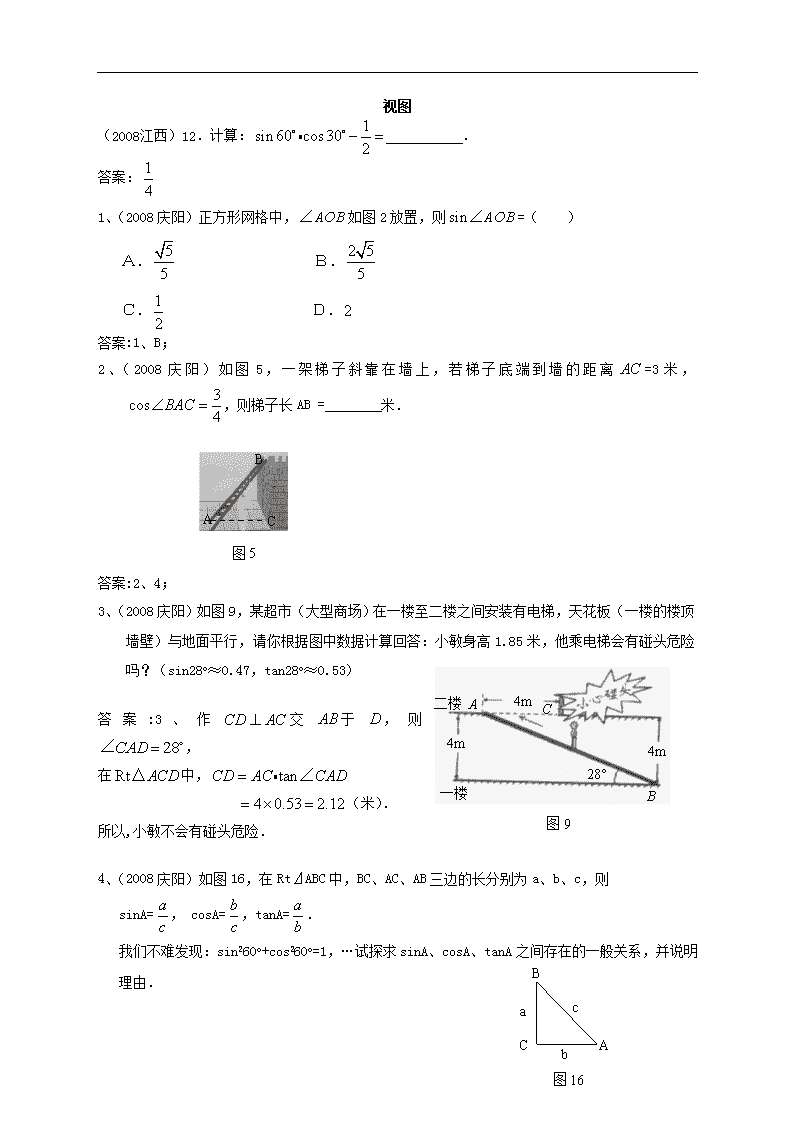
视图 ‎（2008江西）12．计算： 　　 ．‎ 答案：‎ ‎1、（2008庆阳）正方形网格中，如图2放置，则=（　　）‎ Ａ． Ｂ．‎ Ｃ． Ｄ．‎ 答案:1、B；‎ ‎2、（2008庆阳）如图5，一架梯子斜靠在墙上，若梯子底端到墙的距离=‎3米，，则梯子长AB = 米．‎ A B C 图5‎ 答案:2、4；‎ 二楼 一楼 ‎4m A ‎4m ‎4m B ‎28°‎ C 图9‎ ‎3、（2008庆阳）如图9，某超市（大型商场）在一楼至二楼之间安装有电梯，天花板（一楼的楼顶墙壁）与地面平行，请你根据图中数据计算回答：小敏身高‎1.85米，他乘电梯会有碰头危险吗？（sin28o≈0.47，tan28o≈0.53）‎ 答案:3、作交于，则， ‎ 在中， ‎ ‎（米）． ‎ 所以,小敏不会有碰头危险．‎ ‎4、（2008庆阳）如图16，在Rt⊿ABC中，BC、AC、AB三边的长分别为a、b、c，则 ‎ sinA=， cosA=，tanA=．‎ b A C B c a 图16‎ ‎ 我们不难发现：sin260o+cos260o=1，… 试探求sinA、cosA、tanA之间存在的一般关系，并说明理由．‎ 答案:4、存在的一般关系有：‎ ‎（1） sin‎2A+cos‎2A=1；‎ ‎（2）tanA=． ‎ b A C B c a ‎（1） 证明：∵ sinA=, cosA=, ‎ a2+b2=c2, ‎ ‎∴ sin‎2A+cos‎2A==1． ‎ ‎（2） 证明：∵ sinA=, cosA=, ‎ ‎∴ tanA== =．‎ ‎5、（2008杭州）在直角坐标系中，点在第一象限内，且与轴正半轴的夹角为，则的值是（ ）‎ A． B． C． D．‎ 答案：B；‎ C A B D ‎（第7题图）‎ ‎（2008温州）7 .如图，在中，是斜边上的中线，‎ 已知，，则的值是（ ）‎ A． B． C． D．‎ 答案C ‎（2008金华）15.把两块含有30o的相同的直角三角尺按如图所示摆放，使 A C B D E ‎（第15题图）‎ 点C、B、E在同一直线上,连结CD,若AC=‎6cm,则△BCD的 面积是 cm2.‎ 答案27‎ ‎1、（2008 嘉兴）如图，正方形中，是边上一点，以为圆心、为半径的半圆与以为圆心，为半径的圆弧外切，则的值为（ ）‎ A． B． C． D．‎ ‎（第1题）‎ 答案：D ‎2、（2008 绍兴）地震发生后，一支专业搜救队驱车前往灾区救援．如图，汽车在一条南北走向的公路上向北行驶，当在处时，车载GPS（全球卫星定位系统）显示村庄在北偏西方向，汽车以‎35km/h的速度前行2h到达处，GPS显示村庄在北偏西方向．‎ ‎（1）求处到村庄的距离；‎ ‎（2）求村庄到该公路的距离．（结果精确到0.1km）‎ ‎（参考数据：，，，‎ A N B C ‎（第2题图）‎ ‎）‎ 解：过作，交于．‎ ‎（1），，‎ ‎，‎ A N B C ‎， ‎ 即处到村庄的距离为‎70km．‎ ‎（2）在中，‎ ‎．‎ 即村庄到该公路的距离约为‎55.2km．‎ ‎(2008甘肃白银)图18‎ 如图18，在梯形ABCD中，AD∥BC，∠B=90°，AD=2，BC=5，tanC=．‎ ‎（1）求点D到BC边的距离；‎ ‎（2）求点B到CD边的距离．‎ 解：（1）如图①，作DE⊥BC于E， ‎ ‎∵ AD∥BC，∠B=90°，∴ ∠A=90°．又∠DEB=90°，‎ 图①‎ ‎∴ 四边形ABED是矩形． ∴ BE=AD=2， ∴ EC=BC-BE=3． ‎ 在Rt△DEC中，DE= EC·tanC ==4． ‎ ‎（2）如图②，作BF⊥CD于F． ‎ 方法一：‎ 图②‎ 在Rt△DEC中，∵ CD=5，∴ BC=DC，又∠C=∠C， 8分 ‎ ‎∴ Rt△BFC≌Rt△DEC． ∴ BF= DE=4． ‎ 方法二： ‎ 在Rt△DEC中，∵ CD=5， ∴ sinC=． ‎ 在Rt△BFC中，BF=BC·sinC==4． ‎ ‎(2008甘肃白银)如图22（1），由直角三角形边角关系，可将三角形面积公式变形，‎ b B A C c 图22 (1)‎ 得 =bc·sin∠A． ①‎ 即 三角形的面积等于两边之长与夹角正弦之积的一半． ‎ 如图22（2），在⊿ABC中，CD⊥AB于D，∠ACD=α， ∠DCB=β．‎ ‎∵ ， 由公式①，得 B D A α β C 图22 (2)‎ AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ，‎ 即 AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ． ②‎ 你能利用直角三角形边角关系，消去②中的AC、BC、CD吗？不能，‎ 说明理由；能，写出解决过程．‎ 解：能消去AC、BC、CD，得到sin(α+β)= sinα·cosβ+cosα·sinβ． ‎ 解：给AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ两边同除以AC·BC，得 A B O 图2‎ sin(α+β)= ·sinα+·sinβ， ∵ =cosβ， =cosα． ‎ ‎∴ sin(α+β)= sinα·cosβ+cosα·sinβ． ‎ ‎（2008甘肃兰州）正方形网格中，如图2放置，则的值为（ A ）‎ A． B． C． D．2‎ ‎（2008甘肃兰州）D B C 图10‎ A ‎60米 如图10，小明在楼顶处测得对面大楼楼顶点处的仰角为 ‎52°，楼底点处的俯角为13°．若两座楼与相距‎60米，则楼的高 度约为 米．（结果保留三个有效数字）（，，，，，）‎ 答案：90.6‎ ‎1. （2008哈尔滨市T23） 如图，一艘轮船位于灯塔P的北偏东60°‎ 方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处．求此时轮船所在的B处与灯塔P的距离（结果保留根号）．‎ ‎23．解：过点作垂足为 ‎ 则 ‎ 在中， ‎ 在中，‎ ‎ ‎ 当轮船位于灯塔南偏东方向时轮船与灯塔的距离是海里 答：当轮船位于灯塔南偏东方向时轮船与灯塔的距离是海里 ‎1.（2008山东济南）某大草原上有一条笔直的公路，在紧靠公路相距40千米的A、B两地，分别有甲、乙两个医疗站，如图，在A地北偏东45°、B地北偏西60°方向上有一牧民区C．一天，甲医疗队接到牧民区的求救电话，立刻设计了两种救助方案，方案I：从A地开车沿公路到离牧民区C最近的D处，再开车穿越草地沿DC方向到牧民区C．方案II：从A地开车穿越草地沿AC方向到牧民区C． 已知汽车在公路上行驶的速度是在草地上行驶速度的3倍．‎ ‎（1）求牧民区到公路的最短距离CD．‎ ‎（2）你认为甲医疗队设计的两种救助方案，哪一种方案比较合理？并说明理由． ‎ A D Ｂ 北 C 东 ‎45°‎ ‎60°‎ 第22题图 ‎（结果精确到0.1．参考数据：取1.73，取1.41）‎ ‎．解:（1）设CD为千米，‎ 由题意得，∠CBD=30°，∠CAD=45°‎ ‎∴AD=CD=x 1分 A D Ｂ C ‎45°‎ ‎60°‎ 第22题图 在Rt△BCD中，tan30°=‎ ‎∴ BD= 2分 AD+DB=AB=40‎ ‎∴ 3分 解得 ≈14.7 ‎ ‎∴ 牧民区到公路的最短距离CD为14.7千米． 4分 ‎（若用分母有理化得到CD=14.6千米，可得4分）‎ ‎（2）设汽车在草地上行驶的速度为，则在公路上行驶的速度为3，‎ 在Rt△ADC中，∠CAD=45°，∴ AC=CD 方案I用的时间 5分 方案II用的时间 6分 ‎∴ ‎ ‎= 7分 ‎∵ ＞0 ‎ ‎∴ ＞0 8分 ‎∴方案I用的时间少，方案I比较合理 9分 ‎2. （2008山东青岛）在一次课题学习课上，同学们为教室窗户设计一个遮阳蓬，小明同学绘制的设计图如图所示，其中，AB表示窗户，且AB＝2米，BCD表示直角遮阳蓬，已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18.6°，最大夹角β为64.5°．‎ 请你根据以上数据，帮助小明同学计算出遮阳蓬中CD的长是多少米？（结果保留两个有效数字）‎ ‎（参考数据：sin18.6°＝0.32，tan18.6°＝0.34，sin64.5°＝0.90，tan64.5°＝2.1）‎ A Ｄ Ｃ B Ｄ 解：设BC的长为x米，则AC的长为（2＋x）米，‎ ‎………………1分 由于α为18.6°，β为64.5°，所以∠ADC＝β，∠CDB＝α 在Rt△ACD中，AC＝（x＋2）米，∠ACD＝90°，∠ADC＝64.5°，∴CD＝‎ ‎ ………………2分 在Rt△BCD中，BC＝x米，∠ACD＝90°，∠BDC＝18.6°，∴CD＝‎ ‎ ………………3分 ‎∴＝，∴tan18.6°（x＋2）＝tan64.5°x 即x＝1.5，∴BC＝1.5米， ………………4分 ‎∴CD＝≈4.7（米） ‎ 答：遮阳蓬中CD的长是4.7米. ………………6分 ‎（2008江苏省宿迁）已知为锐角，且，则等于 Ａ．　　　Ｂ．　　　Ｃ．　　　Ｄ．‎ 答案选C ‎16．(2008安徽)小明站在处放风筝，风筝飞到处时的线长为20米，这时测得，若牵引线底端离地面1.5米，求此时风筝离地面的高度．（计算结果精确到0.1米，）‎ 第16题图 C B A E D ‎[解]‎ 在中，．‎ 又，‎ ‎（米）．‎ 答：此时风筝离地面的高度约是18.8米．‎ ‎17．(2008芜湖)（本题共两小题，每小题6分，满分12分）‎ 计算：．答案原式 ‎ ‎ ‎ ‎18．(2008芜湖) （本小题满分8分）‎ 在我市迎接奥运圣火的活动中，某校教学楼上悬挂着宣传条幅DC，小丽同学在点A处，测得条幅顶端D的仰角为30°，再向条幅方向前进10米后， 又在点B处测得条幅顶端D的仰角为45°，已知测点A、B和C离地面高度都为1.44米，求条幅顶端D点距离地面的高度．（计算结果精确到0.1米， 参考数据:．） ‎ 解: 在Rt△BCD中， ，∴． 在Rt△ACD中， ，‎ ‎∴． ‎ ‎∴．∴． ‎ ‎∴（米） ‎ ‎∴条幅顶端D点距离地面的高度为（米）． ‎ ‎（2008年江苏省南通市，21T，7分）如图，海上有一灯塔P，在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行，行至A点处测得灯塔P在它的北偏东60°的方向上，继续向东行驶20分钟后，到达B处又测得灯塔P在它的北偏东45°方向上，如果海轮不改变方向继续前进有没有暗礁的危险？‎ ‎21．解：过点P作PC⊥AB于C点，根据题意，得 AB＝18×＝6，∠PAB＝90°－60°＝30°，∠PBC＝90°－45°＝45°，∠PCB＝90°，‎ ‎∴PC＝BC 在Rt△PAC中 tan30°＝＝‎ 即，解得PC＝＋3‎ ‎∵＋3＞6，∴海轮不改变方向继续前进无触礁危险 ‎（2008青海）M N B A 第24题图 24．《中华人民共和国道路交通管理条理》规定：“小汽车在城市街道上的行驶速度不得超过千米/时．”如图所示，已知测速站到公路的距离为‎30米，一辆小汽车在公路上由东向西行驶，测得此车从点行驶到点所用的时间为2秒，并测得，．计算此车从到的平均速度为每秒多少米（结果保留两个有效数字），并判断此车是否超过限速．（参考数据：，）‎ 答案：解：在中，‎ ‎． （2分）‎ 在中，‎ ‎． （4分）‎ ‎． （5分）‎ 则到的平均速度为：‎ ‎（米/秒）． （6分）‎ ‎70千米/时米/秒米/秒米/秒， （7分）‎ 此车没有超过限速． （8分）‎ ‎（2008赤峰）C B A 第11题图 10．在中，，，，则（D ）‎ A． B． C． D．‎ ‎（2008赤峰）北 O A B 23.如图，在海岸边有一港口．已知：小岛在港口北偏东的方向，小岛在小岛正南方向，海里，海里．计算：‎ ‎（1）小岛在港口的什么方向？‎ ‎（2）求两小岛的距离．‎ 解：过作垂直于交的延长线于． （1分）‎ ‎（1）在中，‎ 北 O A B C ‎，‎ ‎，‎ ‎（海里） （5分）‎ 在中，‎ ‎，‎ ‎．‎ 小岛在港口的北偏东（答东偏北亦可） （9分）‎ ‎（2）由（1）知，‎ 所以（海里）‎ 答：两小岛的距离为海里． ‎ ‎(2008宁夏)18.如图，在△中，∠=90°，sin=，=15，求△的周长和tan的值．‎ 解：在中, ∠=90°, =15‎ ‎==, ‎ ‎∴ 3分 ‎ ‎∴△的周长为36 5分 ‎ A= ‎ ‎10．（08南京）如图，已知的半径为1，与相切于点，与交于点，，垂足为，则的值等于（ A ）‎ A． B． C． D．‎ 23．（08南京）（6分）如图，山顶建有一座铁塔，塔高，某人在点处测得塔底的仰角为，塔顶的仰角为，求此人距的水平距离．‎ ‎（第23题）‎ A B C D ‎（参考数据：，，，，，）‎ 解：在中，，‎ ‎． 2分 在中，，‎ ‎． 4分 ‎．‎ ‎．‎ 答：此人距的水平距离约为500m． 6分 11．（08连云港）在中，，，，则 ．‎ ‎[2008福建省南平市]24．（12分）2008年初，我国南方部分省区发生了雪灾，造成通讯受阴．如图，现有某处山坡上一座发射塔被冰雪从处压折，塔尖恰好落在坡面上的点处，在处测得点的仰角为，塔基的俯角为，又测得斜坡上点到点的坡面距离为‎15米，求 折断前发射塔的高．（精确到‎0.1米）‎ 24．解：作于，由已知得：，，米 在中，，‎ ‎ 3分 ‎，‎ ‎ 5分 在中，‎ ‎ 8分 ‎， 10分 ‎ 11分 答：折断前发射塔的高约为34.1米． 12分 注意：按以下方法进行近似计算视为正确，请相应评分．‎ ‎①若到最后再进行近似计算结果为：‎ ‎；‎ ‎②若解题过程中所有三角函数值均先精确到0.01，则近似计算的结果为：‎ ‎．‎ ‎[2008年福建省宁德市]22．（本题满分10分）曙光中学需制作一副简易篮球架，如图是篮球架的侧面示意图，已知篮板所在直线AD和直杆EC都与BC垂直，BC＝‎2.8米，CD＝‎1.8米，∠ABD＝40°，求斜杆AB与直杆EC的长分别是多少米？（结果精确到‎0.01米）‎ D C B A E 解：‎ ‎22.解：在Rt△BAD中 ‎∵，∴（米）．‎ 在Rt△BEC中，‎ ‎∵，∴（米）．‎ 则斜杆AB与直杆EC的长分别是2.35米和6.00米．‎ ‎（2008 大连市）22．水平地面上的甲、乙两楼的距离为‎30米，从甲楼顶部测得乙楼顶部的仰角为30°，测行乙楼底部的俯角为45°．‎ ‎⑴请你画出测量示意图(大楼的长、宽忽略不计)；‎ ‎⑵求甲、乙两楼的高度．‎ ‎．解：（1）如图1．………………………………………………2分 ‎（2）过点B作BE⊥CD，垂足为E．‎ ‎∵BA⊥AC，CD⊥AC，∴四边形ABEC为矩形，………………………………………………3分 ‎∴AB＝EC,BE＝AC,BE∥AC．………………………………………………4分 ‎∴∠ACB=∠EBC=45°．………………………………………………5分 ‎∴AB=AC=30．………………………………………………6分 在Rt△BED中，tan∠DBE=，………………………………………………7分 ‎∴DE=BE×tan∠DBE=30tan30°=．………………………………………………8分 ‎∴CD=CE+DE=AB+DE=30+．………………………………………………9分 答：甲、乙两楼的高分别为‎30米、（30+）米．………………………………………10分 ‎24．(08荆门) (8分)如图16，山脚下有一棵树AB，小华从点B沿山坡向上走50米到达点D，用高为1.5米的测角仪CD没得树顶的仰角为10°，已知山坡的坡角为15°，求树AB的高(精确到0.1米)．‎ ‎(已知：sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27)‎ 图16‎ 解：延长CD交PB于F，则DF⊥PB．‎ F ‎∴DF=BD·sin15°≈50×0.26=13.0． …………2分 ‎ (写13不扣分) ‎ ‎ ∴CE=BF=BD·cos15°≈50×0.97=48.5． …………4分 ‎ ∴AE=CE·tan10°≈48.5×0.18=8.73． …………6分 ‎ ∴AB=AE＋CD＋DF=8.73＋1.5＋13 =23.2．‎ ‎ 答：树高约为23.2米． ………………………8分 ‎24．(08泰州)如图，某堤坝的横截面是梯形，背水坡的坡度i（即）为1∶1.2，坝高为5米．现为了提高堤坝的防洪抗洪能力，市防汛指挥部决定加固堤坝，要求坝顶加宽1米，形成新的背水坡，其坡度为1∶1.4．已知堤坝总长度为4000米．‎ ‎（1）求完成该工程需要多少土方？（4分）‎ ‎（2）该工程由甲、乙两个工程队同时合作完成，按原计划需要20天．准备开工前接到上级通知，汛期可能提前，要求两个工程队提高工作效率．甲队工作效率提高30%，乙队工作效率提高40%，结果提前5天完成．问这两个工程队原计划每天各完成多少土方？（5分）‎ C D E A F B 第24题图 ‎（1）作DG⊥AB于G，作EH⊥AB于H．‎ ‎∵CD∥AB, ∴EH=DG=‎5米,‎ ‎∵,∴AG=‎6米，…………………………………………1分 ‎∵,∴FH=‎7米， …………………………………………2分 ‎∴FA=FH＋GH－AG=7＋1－6=2（米）…………………………………3分 ‎∴SADEF=.‎ V=7.5×4000=30000（立方米）. ……………………………………4分 ‎（2）设甲队原计划每天完成x立方米土方, 乙队原计划每天完成y立方米土方.‎ 根据题意，得 …………………6分 化简，得…………………………………………7分 解之，得 ……………………………………………………………8分 答：甲队原计划每天完成1000立方米方土, ‎ 乙队原计划每天完成500立方米方土. ……………………………9分 ‎1、（1T）（2008湖北省黄冈市，3分） ．‎ ‎2、(5T)(湖北省襄樊,3分)在正方形网格中，的位置如图 ‎2所示，则的值为（ B ）‎ A． B． C． D．‎ ‎3、(15T)(湖北省襄樊,3分)如图8，张华同学在学校某建筑物的点处测得旗杆顶部点的仰角为，旗杆底部点的俯角为．若旗杆底部点到建筑物的水平距离米，旗杆台阶高1米，则旗杆顶点离地面的高度为 米（结果保留根号）．15．‎ A C B a c b ‎（5题图）‎ 5．（2008内江市）如图，在中，，三边分别为，‎ 则等于（ ）‎ A． B． C． D．‎ 答案：D ‎22．（2008资阳市）（本小题满分10分）‎ 如图8，小唐同学正在操场上放风筝，风筝从A处起飞，几分钟后便飞达C处，此时，在AQ延长线上B处的小宋同学，发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.‎ ‎（1）已知旗杆高为‎10米，若在B处测得旗杆顶点P的仰角为30°，A处测得点P的仰角为45°，试求A、B之间的距离；‎ 图8‎ ‎（2）此时，在A处背向旗杆又测得风筝的仰角为75°，若绳子在空中视为一条线段，求绳子AC约为多少？（结果可保留根号）‎ 答案：(1) 在Rt△BPQ中，PQ=‎10米，∠B=30°，‎ 则BQ=cot30°×PQ＝, 2分 图8‎ 又在Rt△APQ中，∠PAB=45°，‎ 则AQ=cot45°×PQ=10， ‎ 即：AB=(+10)(米)； 5分 ‎(2) 过A作AE⊥BC于E，‎ 在Rt△ABE中，∠B=30°，AB=+10，‎ ‎∴ AE=sin30°×AB=（+10）=5+5， 7分 ‎∵∠CAD=75°，∠B=30°，‎ ‎∴ ∠C=45°， 8分 在Rt△CAE中，sin45°＝，‎ ‎∴AC=（5+5）=(5+5)(米) 10分 1. ‎（2008黄石）A P 东 北 如图，甲船在港口的北偏西方向，距港口海里的处，沿方向以12海里/时的速度驶向港口．乙船从港口出发，沿北偏东方向匀速驶离港口，现两船同时出发，2小时后乙船在甲船的正东方向．求乙船的航行速度．（精确到0.1海里/时，参考数据，）‎ 答案：解：依题意，设乙船速度为海里/时，2小时后甲船在点处，乙船在点处，作于，则海里，海里．‎ 在中，，‎ ‎． （2分）‎ 在中，，‎ ‎． （4分）‎ ‎，‎ ‎．‎ ‎．‎ 答：乙船的航行速度约为19.7海里/时． （7分）‎ ‎(2008中山市)11．计算 ：.‎ 解：‎ 原式 ‎（济宁市2008）12．如图，丁轩同学在晚上由路灯走向路灯，当他走到点时，发现身后他影子的顶部刚好接触到路灯的底部，当他向前再步行‎20m到达点时，发现身前他影子的顶部刚好接触到路灯的底部，已知丁轩同学的身高是‎1.5m，两个路灯的高度都是‎9m，则两路灯之间的距离是（ ）‎ A．‎24m B．‎25m C．‎28m D．‎‎30m 答案：D ‎（滨州市2008）‎ ‎22、如图，AC是某市坏城路的一段，AE、BF、CD都是南北方向的街道，其与环城路AC的交叉路口分别是A、B、C经测量花卉世界D位于点A的北偏东45°方向，点B的北偏东30°方向上，AB=‎2km，∠DAC=15°.‎ ‎（1）求∠ADB的大小；（2）求B、D之间的距离；（3）求C、D之间的距离. ‎ 答案：22．解（1）如图，由题得，‎ ‎（2）由（1）知 即B、D之间的距离为‎2km。‎ ‎（3）过B作，交其延长线于点O，‎ 在中，‎ ‎ ‎ ‎(2008福州市)‎ ‎16．（每小题7分，满分14分）‎ ‎（1）计算：‎ 答案解：（1）原式．‎ ‎（第10题图）‎ ‎(2008龙岩市)‎ ‎10．如图，在Rt△ABC中，∠CAB=90°，AD是∠CAB的平分线，tanB=，则CD∶DB= .‎ ‎17．已知α为锐角，则m=sinα+cosα的值（ ）‎ ‎ A．m＞1 B．m=‎1 ‎C．m＜1 D．m≥1‎ 答案A ‎（第16题图）‎ ‎18．（8分）计算：20080+|-1|-cos30°+ ()3.‎ 答案解：原式=1＋1－×＋=2－＋= . ‎ ‎（2008年贵阳市）19．（本题满分10分）‎ 如图7，某拦河坝截面的原设计方案为：，坡角，坝顶到坝脚的距离．为了提高拦河坝的安全性，现将坡角改为，由此，点需向右平移至点，请你计算的长（精确到‎0.1m）．‎ 如图7，过点A作AE⊥BC于点E，过点D作DF⊥BC于点F． 2分 ‎（图7）‎ A B C D H C F E 在Rt△ABE中，，‎ ‎． 4分 ‎ ，‎ ‎． 6分 AH∥BC DF = AE ≈ 5.77 7分 在中，，‎ ‎． 9分 ‎（米）． 10分 ‎(2008 河南)2.直角三角形在正方形网格纸中的位置如图所示，则的值是（ ）‎ A. B. C. D. ‎ 答案：D ‎(2008 河南)21、（本题满分10分）‎ 如图，在小山的西侧A处有一热气球，以30米/分钟的速度沿着与垂直方向所成夹角为30°的方向升空，40分钟后到达C处，这时热气球上的人发现，在A处的正东方向有一处着火点B，十分钟后，在D处测得着火点B的俯角为15°，求热气球升空点A与着火点B的距离。（结果保留根号，参考数据：‎ ‎(，，，）。‎ 答案：（本小题满分10分）‎ 解：由题意可知，AD＝(40＋10)×30＝1500（米）···1分 过点D作DH⊥BA，交BA延长线于点H。·········2分 在Rt△DAH中，DH＝AD·sin60°‎ ‎＝1500×＝750（米）。····4分 AH＝AD·cos60°＝1500×＝750（米）。·······6分 在Rt△DBH中，‎ BH＝DH·cot15°＝750×(2＋)＝（1500＋2250）（米）···8分 ‎∴BA＝BH－AH＝1500＋2250－750＝1500（＋1）（米）………..9分 答：热气球升空点A与着火点B的距离为1500（＋1）（米）……10分 ‎（2008湖北武汉A O B 东 北 8）. 如图，小雅家（图中点Ｏ处）门前有一条东西走向的公路，经测得有一水塔（图中点Ａ处）在她家北偏东60度‎500m处，那么水塔所在的位置到公路的距离AB是（　　）．‎ Ａ.250ｍ　　　Ｂ．ｍ　　Ｃ．ｍ　　　　Ｄ．ｍ．‎ 答案：A ‎（2008肇庆市）17.在Rt△ABC中，∠C = 90°，a =3 ，c =5，求sinA和tanA的值.‎ 答案：解：在Rt △ABC中，c=5，a=3．‎ ‎∴ ‎ ‎∴ ‎ ‎ ．‎ ‎(2008中山市)11．计算 ：.‎ 解：‎ 原式 ‎(2008中山市)A D B E 图6‎ i=1:‎ C 19．）如图6，梯形ABCD是拦水坝的横断面图，（图中是指坡面的铅直高度DE与水平宽度CE的比），‎ ‎∠B=60°，AB=6，AD=4，求拦水坝的横断面ABCD的面积．（结果保留三位有效数字.参考数据：≈1.732，≈1.414）‎ ‎19.解：过点A作AF⊥BC，垂足为点F.‎ ‎ 在Rt△ABF中，∠B=60°,AB=6,‎ ‎ ∴ ‎ ‎.‎ ‎ ‎ ‎ ‎ ‎ .‎ ‎ ∵ AD∥BC,AF⊥BC,DE⊥BC,‎ ‎ ∴ 四边形AFED是矩形，‎ ‎ ∴ , .‎ 在Rt△CDE中，，‎ ‎ ∴ ,‎ ‎ ∴ .‎ ‎ ∴ ‎ ‎ ‎ ‎.‎ 答：拦水坝的横断面ABCD的面积约为52.0面积单位.‎ ‎（2008浙江台州）15．如图，四边形，，都是正方形，边长分别为；五点在同一直线上，则 （用含有的代数式表示）．‎ a D C B A M c N E F b G H ‎（第15题）‎ 答案：‎ ‎（2008浙江台州）21．如图是某宾馆大厅到二楼的楼梯设计图，已知米，米，中间平台宽度为‎2米，为平台的两根支柱，垂直于，垂足分别为，，．‎ 求和的水平距离．（精确到‎0.1米，参考数据：，）‎ A N M B F C E D ‎（第21题）‎ 答案：21．解：设米．‎ ‎，，‎ 米，‎ 米，‎ 米，‎ 米，米，米，‎ A N M B F C E D ‎（第21题）‎ 米，‎ 在中，，，‎ ‎，‎ 即．‎ 解这个方程得：．‎ 答：支柱距的水平距离约为‎4.6米．‎ ‎（2008浙江温州）10．以OA为斜边作等腰直角三角形OAB，再以OB为斜边在△OAB外侧作等腰直角三角形OBC，如此继续，得到8个等腰直角三角形（如图），则图中△OAB与△OHJ的面积比值是（　　）‎ ‎（A）32 （B）64 （C）128 （D）256‎ B A C D E F G H I O ‎（第10题图）‎ 答案：C ‎（2008浙江温州）24．（本题14分）如图，在Rt△ABC中，∠A＝90º，AB＝6，AC＝8，D，E分别是边AB，AC的中点，点P从点D出发沿DE方向运动，过点P作PQ⊥BC于Q，过点Q作QR∥BA交AC于R，当点Q与点C重合时，点P停止运动．设BQ＝x，QR＝y．‎ ‎（1）求点D到BC的距离DH的长；‎ ‎（2）求y关于x的函数关系式（不要求写出自变量的取值范围）；‎ A B C D E R P H Q ‎（第24题图）‎ ‎（3）是否存在点P，使△PQR为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由．‎ 答案：24． （本题14分）‎ 解：（1），，，．‎ 点为中点，．‎ ‎，．‎ ‎，‎ ‎，．‎ ‎（2），．‎ ‎，，‎ ‎，，‎ 即关于的函数关系式为：．‎ ‎（3）存在，分三种情况：‎ A B C D E R P H Q M ‎2‎ ‎1‎ ‎①当时，过点作于，则．‎ ‎，，‎ ‎．‎ ‎，，‎ A B C D E R P H Q ‎，．‎ A B C D E R P H Q ‎②当时，，‎ ‎．‎ ‎③当时，则为中垂线上的点，‎ 于是点为的中点，‎ ‎．‎ ‎，‎ ‎，．‎ 综上所述，当为或6或时，为等腰三角形．‎ ‎（2008·上海）“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上，导致其中部分图形和数据看不清楚（如图7所示）．已知图纸上的图形是某建筑物横断面的示意图，它是以圆的半径所在的直线为对称轴的轴对称图形，是与圆的交点．‎ O C A D E H 图8‎ 图7‎ ‎（1）请你帮助小王在图8中把图形补画完整；‎ ‎（2）由于图纸中圆的半径的值已看不清楚，根据上述信息（图纸中是坡面的坡度），求的值．‎ 解：（1）（图形正确）； （3分）‎ ‎（2）解：由已知，垂足为点，则．‎ ‎，． （1分）‎ 在中，．设，，又，‎ 得，解得．，． （3分）‎ ‎，，．‎ 在中，，．‎ 解得．‎ ‎（2008年遵义市）24．（10分）我市某乡镇学校教学楼后面靠近一座山坡，坡面上是一块平地，如图所示．，斜坡米，坡角，为防夏季因瀑雨引发山体滑坡，保障安全，学校决定对山坡进行改造．经地质人员勘测，当坡角不超过时，可确保山体不滑坡，改造时保持坡脚不动，从坡顶沿削进到处，问至少是多少米（结果保留根号）？‎ 解：作BG⊥AD于G，作EF⊥AD于F，则在Rt△ABG中，∠BAD=600，AB=40，‎ 所以就有BG =AB·Sin600D A B C E F G =20，‎ AG = AB·Cos600=20‎ 同理在Rt△AEF中，∠EAD=450，‎ 则有AF=EF=BG=20，‎ 所以BE=FG=AF-AG=20()米。‎