2017-2018学年四川省凉山州九年级上期末数学试卷含答案解析 19页

‎2017-2018学年四川省凉山州九年级（上）期末数学试卷 ‎　‎ 一、选择题（每题3分，共39分）‎ ‎1．（3分）将一元二次方程5x2﹣1=4x化成一般形式后，二次项系数和一次项系数分别为（　　）‎ A．5，﹣1 B．5，4 C．5，﹣4 D．5x2，﹣4x ‎2．（3分）抛物线y=2（x+m）2+n（m，n是常数）的顶点坐标是（　　）‎ A．（m，n） B．（﹣m，n） C．（m，﹣n） D．（﹣m，﹣n）‎ ‎3．（3分）下列图形中，既是轴对称图形又是中心对称图形的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎4．（3分）两个同心圆中大圆的弦AB与小圆相切于点C，AB=8，则形成的圆环的面积为（　　）‎ A．无法求出 B．8 C．8π D．16π ‎5．（3分）同时投掷两枚普通的正方体骰子，所得两个点数之和大于9的概率是（　　）[来源:学&科&网Z&X&X&K]‎ A． B． C． D．‎ ‎6．（3分）若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有两个不相等的实数根，则k的取值范围是（　　）‎ A．k＞ B．k≥ C．k＞且k≠1 D．k≥且k≠1‎ ‎7．（3分）当ab＞0时，y=ax2与y=ax+b的图象大致是（　　）‎ A． B． C． D．‎ ‎8．（3分）⊙O的内接正三角形和外切正方形的边长之比是（　　）‎ A．：2 B．1：1 C．1： D．：‎ ‎9．（3分）若函数，则当函数值y=8时，自变量x的值是（　　）‎ A．± B．4 C．±或4 D．4或﹣‎ ‎10．（3分）下列事件中必然发生的是（　　）‎ A．抛两枚均匀的硬币，硬币落地后，都是正面朝上 B．掷一枚质地均匀的骰子，朝上一面的点数是3‎ C．通常情况下，抛出的篮球会下落 D．阴天就一定会下雨 ‎11．（3分）如图的方格纸中，左边图形到右边图形的变换是（　　）‎ A．向右平移7格 B．以AB的垂直平分线为对称轴作轴对称变换，再以AB为对称轴作轴对称变换 C．绕AB的中点旋转180°，再以AB为对称轴作轴对称 D．以AB为对称轴作轴对称，再向右平移7格 ‎12．（3分）若关于x的一元二次方程的两个根为x1=1，x2=2，则这个方程可能是（　　）‎ A．x2+3x﹣2=0 B．x2+3x+2=0 C．x2﹣3x+2=0 D．x2﹣2x+3=0‎ ‎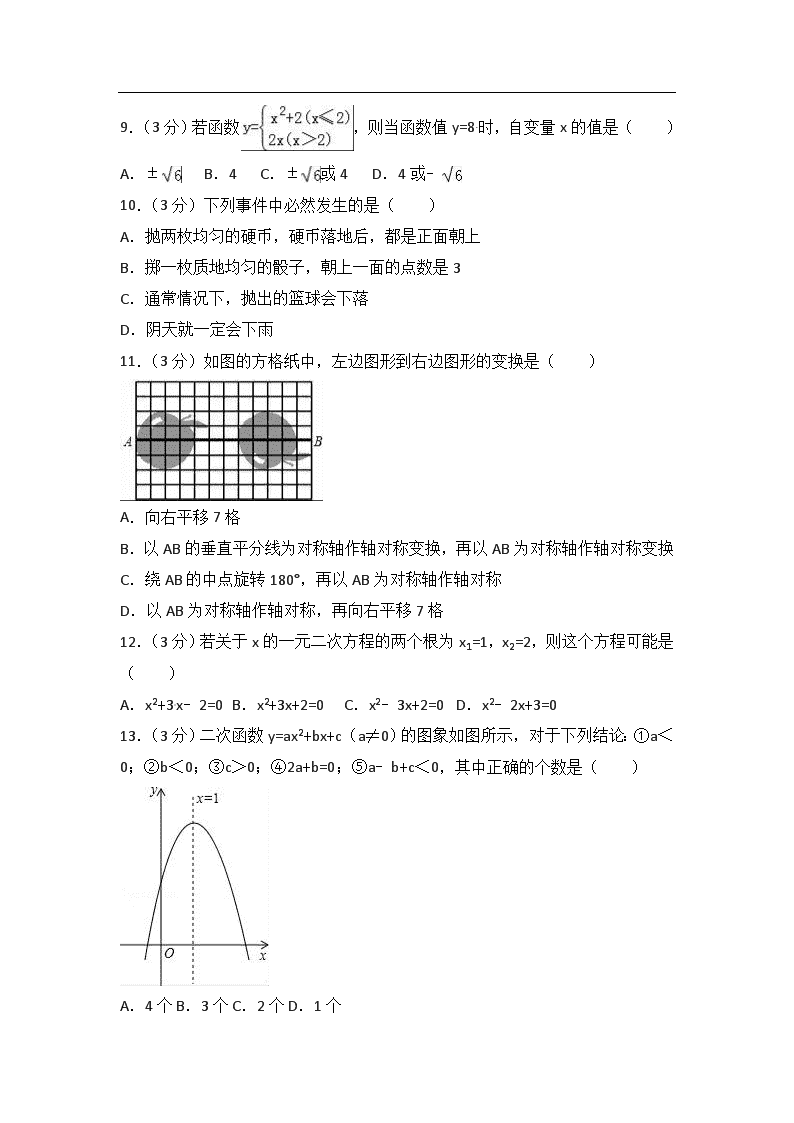13．（3分）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对于下列结论：①a＜0；②b＜0；③c＞0；④2a+b=0；⑤a﹣b+c＜0，其中正确的个数是（　　）[来源:学科网ZXXK]‎ A．4个 B．3个 C．2个 D．1个 ‎　‎ 二、填空题（每题3分，共15分）‎ ‎14．（3分）某种品牌的电脑，原价是7200元/台，经过连续两次降价后，现价是3528元/台，平均每次降价的百分率为　 　．‎ ‎15．（3分）飞机着陆后滑行的距离y（单位：m）关于滑行的时间x（单位：s）的函数解析式是y=﹣1.2x2+48x，则飞机着陆后滑行　 　m后才能停下来．‎ ‎16．（3分）圆锥的母线长5cm，底面半径长3cm，那么它的侧面展开图的圆心角是　 　度．‎ ‎17．（3分）如图，四边形ABCD中，∠BAD=∠C=90°，AB=AD，AE⊥BC于E，若线段AE=5，则S四边形ABCD=　 　．‎ ‎18．（3分）在平面直角坐标系中，O为原点，⊙O的半径为7，直线y=mx﹣3m+4交⊙O于A、B两点，则线段AB的最小值为　 　．‎ ‎　‎ 三、解答题（共46分）‎ ‎19．（6分）解方程： =1﹣．‎ ‎20．（6分）如图，有一个可以自由转动的转盘被平均分成3个扇形，分别标有1、2、3三个数字，小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束得到一组数（若指针指在分界线时重转）．‎ ‎（1）请你用树状图或列表的方法表示出每次游戏可能出现的所有结果；‎ ‎（2）求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率．‎ ‎21．（6分）某商店在销售中发现：“米奇”牌童装平均每天可售出2‎ ‎0件，每件赢利40元．为了迎“六一”儿童节，商场决定适当地降价，以扩大销售量，增加盈利，减少库存．经市场调查发现，如果每件童装每降价4元，那么平均每天就可多售出8件，要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少元？‎ ‎22．（7分）如图，方格纸中每个小正方形的边长都是1个单位长度，△ABC在平面直角坐标系中的位置如图所示．‎ ‎（1）将△ABC向上平移3个单位后，得到△A1B1C1，请画出△A1B1C1，并直接写出点A1的坐标．‎ ‎（2）将△ABC绕点O顺时针旋转90°，请画出旋转后的△A2B2C2，并求点B所经过的路径长（结果保留x）‎ ‎23．（6分）已知关于x的一元二次方程x2﹣（2k+1）x+4k﹣3=0．‎ ‎（1）求证：无论k取什么实数值，该方程总有两个不相等的实数根；‎ ‎（2）当Rt△ABC的斜边长a为，且两条直角边的长b和c恰好是这个方程的两个根时，求△ABC的周长．‎ ‎24．（6分）如图，△ABC内接于半圆，AB为直径，过点A作直线MN，若∠MAC=∠ABC ‎（1）求证：MN是该圆的切线 ‎（2）设D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F，求证：FD=FG．‎ ‎25．（9分）已知二次函数y=x2﹣2mx+m2﹣1．‎ ‎（1）当二次函数的图象经过坐标原点O（0，0）时，求二次函数的解析式；‎ ‎（2）如图，当m=2时，该抛物线与y轴交于点C，顶点为D，求C、D两点的坐标；‎ ‎（3）在（2）的条件下，x轴上是否存在一点P，使得PC+PD最短？若P点存在，求出P点的坐标；若P点不存在，请说明理由．‎ ‎　‎ ‎2017-2018学年四川省凉山州九年级（上）期末数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（每题3分，共39分）‎ ‎1．（3分）将一元二次方程5x2﹣1=4x化成一般形式后，二次项系数和一次项系数分别为（　　）‎ A．5，﹣1 B．5，4 C．5，﹣4 D．5x2，﹣4x ‎【解答】解：方程整理得：5x2﹣4x﹣1=0，‎ 则二次项系数和一次项系数分别为5，﹣4．‎ 故选C．‎ ‎　‎ ‎2．（3分）抛物线y=2（x+m）2+n（m，n是常数）的顶点坐标是（　　）‎ A．（m，n） B．（﹣m，n） C．（m，﹣n） D．（﹣m，﹣n）‎ ‎【解答】解：因为抛物线y=2（x+m）2+n是顶点式，根据顶点式的坐标特点，它的顶点坐标是（﹣m，n）．‎ 故选B．‎ ‎　‎ ‎3．（3分）下列图形中，既是轴对称图形又是中心对称图形的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【解答】解：第一个图是轴对称图形，是中心对称图形；‎ 第二个图是轴对称图形，不是中心对称图形；‎ 第三个图是轴对称图形，又是中心对称图形；‎ 第四个图是轴对称图形，不是中心对称图形；‎ 既是轴对称图形，又是中心对称图形的有2个，‎ 故选：B．‎ ‎　‎ ‎4．（3分）两个同心圆中大圆的弦AB与小圆相切于点C，AB=8，则形成的圆环的面积为（　　）‎ A．无法求出 B．8 C．8π D．16π ‎【解答】解：如图所示，‎ ‎∵弦AB与小圆相切，‎ ‎∴OC⊥AB，‎ ‎∴C为AB的中点，‎ ‎∴AC=BC=AB=4，‎ 在Rt△AOC中，根据勾股定理得：OA2﹣OC2=AC2=16，‎ 则形成圆环的面积为πOA2﹣πOC2=π（OA2﹣OC2）=16π，‎ 故选D．‎ ‎ [来源:学+科+网]‎ ‎　‎ ‎5．（3分）同时投掷两枚普通的正方体骰子，所得两个点数之和大于9的概率是（　　）‎ A． B． C． D．‎ ‎【解答】解：同时投掷两枚普通的正方体骰子，一共有36种结果，其中两个点数之和大于9的结果有4+6，5+5，5+6，6+4，6+5，6+6共6种，[来源:Z,xx,k.Com]‎ 所以所得两个点数之和＞9的概率是．‎ 故选A．‎ ‎　‎ ‎6．（3分）若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有两个不相等的实数根，则k的取值范围是（　　）‎ A．k＞ B．k≥ C．k＞且k≠1 D．k≥且k≠1‎ ‎【解答】解：∵关于x的一元二次方程（k﹣1）x2+‎ ‎2x﹣2=0有两个不相等的实数根，‎ ‎∴，‎ 解得：k＞且k≠1．‎ 故选C．‎ ‎　‎ ‎7．（3分）当ab＞0时，y=ax2与y=ax+b的图象大致是（　　）‎ A． B． C． D．‎ ‎【解答】解：根据题意，ab＞0，即a、b同号，‎ 当a＞0时，b＞0，y=ax2与开口向上，过原点，y=ax+b过一、二、三象限；‎ 此时，没有选项符合，‎ 当a＜0时，b＜0，y=ax2与开口向下，过原点，y=ax+b过二、三、四象限；‎ 此时，D选项符合，‎ 故选D．‎ ‎　‎ ‎8．（3分）⊙O的内接正三角形和外切正方形的边长之比是（　　）‎ A．：2 B．1：1 C．1： D．：‎ ‎【解答】解：如图所示：连接CO，过点O，作OE⊥CD于点E，‎ 四边形AMNB是正方形，⊙O切AB于点C，△CFD是⊙O的内接正三角形，‎ 设圆的外切正方形的边长为a，‎ 则CO=BC=，∠COE=30°，‎ ‎∴CE=•cos30°=，‎ ‎∴这个圆的内接正三角形的边长为：2EC=，‎ ‎∴：a=：2．‎ 故选：A．‎ ‎　‎ ‎9．（3分）若函数，则当函数值y=8时，自变量x的值是（　　）‎ A．± B．4 C．±或4 D．4或﹣‎ ‎【解答】解：把y=8代入函数，‎ 先代入上边的方程得x=，‎ ‎∵x≤2，x=不合题意舍去，故x=﹣；[来源:学科网]‎ 再代入下边的方程x=4，‎ ‎∵x＞2，故x=4，‎ 综上，x的值为4或﹣．‎ 故选：D．‎ ‎　‎ ‎10．（3分）下列事件中必然发生的是（　　）‎ A．抛两枚均匀的硬币，硬币落地后，都是正面朝上 B．掷一枚质地均匀的骰子，朝上一面的点数是3‎ C．通常情况下，抛出的篮球会下落 D．阴天就一定会下雨 ‎【解答】解：A、B．D都可能发生，也可能不发生，是随机事件，不符合题意；‎ C、一定会发生，是必然事件，符合题意．‎ 故选C．‎ ‎　‎ ‎11．（3分）如图的方格纸中，左边图形到右边图形的变换是（　　）‎ A．向右平移7格 B．以AB的垂直平分线为对称轴作轴对称变换，再以AB为对称轴作轴对称变换 C．绕AB的中点旋转180°，再以AB为对称轴作轴对称 D．以AB为对称轴作轴对称，再向右平移7格 ‎【解答】解：观察可得：要使左边图形变化到右边图形，首先以AB为对称轴作轴对称，再向右平移7格．‎ 故选D．‎ ‎　[来源:学科网ZXXK]‎ ‎12．（3分）若关于x的一元二次方程的两个根为x1=1，x2=2，则这个方程可能是（　　）‎ A．x2+3x﹣2=0 B．x2+3x+2=0 C．x2﹣3x+2=0 D．x2﹣2x+3=0‎ ‎【解答】解：∵x1=1，x2=2，‎ ‎∴x1+x2=3，x1x2=2，[来源:学科网ZXXK]‎ ‎∴以x1，x2为根的一元二次方程可为x2﹣3x+2=0．‎ 故选C．[来源:学*科*网]‎ ‎　‎ ‎13．（3分）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对于下列结论：①a＜0；②b＜0；③c＞0；④2a+b=0；⑤a﹣b+c＜0，其中正确的个数是（　　）‎ A．4个 B．3个 C．2个 D．1个 ‎【解答】解：如图，①抛物线开口方向向下，则a＜0．故①正确；‎ ‎②∵对称轴x=﹣=1，∴b=﹣2a＞0，即b＞0．故②错误；‎ ‎③∵抛物线与y轴交于正半轴，∴c＞0．故③正确；‎ ‎④∵对称轴x=﹣=1，∴b+2a=0．故④正确；‎ ‎⑤根据图示知，当x=﹣1时，y＜0，即a﹣b+c＜0．故⑤正确．‎ 综上所述，正确的说法是①③④⑤，共有4个．‎ 故选A．‎ ‎　‎ 二、填空题（每题3分，共15分）‎ ‎14．（3分）某种品牌的电脑，原价是7200元/台，经过连续两次降价后，现价是3528元/台，平均每次降价的百分率为　30%　．‎ ‎【解答】解：设平均每次降价的百分率为x，由题意，得 ‎7200（1﹣x）2=3528，‎ 解得：x1=1.7（舍去），x2=0.3．[来源:学科网]‎ 故答案为：30%．‎ ‎　‎ ‎15．（3分）飞机着陆后滑行的距离y（单位：m）关于滑行的时间x（单位：s）的函数解析式是y=﹣1.2x2+48x，则飞机着陆后滑行　480　m后才能停下来．‎ ‎【解答】解：∵﹣1.2＜0，‎ ‎∴当x=﹣=20时，y取得最大值，‎ 此时， =480（m）．‎ 故答案为480．‎ ‎　‎ ‎16．（3分）圆锥的母线长5cm，底面半径长3cm，那么它的侧面展开图的圆心角是　216　度．‎ ‎【解答】解：∵圆锥的底面半径长3cm，‎ ‎∴圆锥的底面周长为6πcm，‎ 设扇形的圆心角为n°，‎ ‎∴=6π，‎ 解得n=216°．‎ ‎　‎ ‎17．（3分）如图，四边形ABCD中，∠BAD=∠C=90°，AB=AD，AE⊥BC于E，若线段AE=5，则S四边形ABCD=　25　．‎ ‎【解答】解：过A点作AF⊥CD交CD的延长线于F点，如图，‎ ‎∵AE⊥BC，AF⊥CF，‎ ‎∴∠AEC=∠CFA=90°，‎ 而∠C=90°，‎ ‎∴四边形AECF为矩形，‎ ‎∴∠2+∠3=90°，‎ 又∵∠BAD=90°，‎ ‎∴∠1=∠2，‎ 在△ABE和△ADF中 ‎∴△ABE≌△ADF，‎ ‎∴AE=AF=5，S△ABE=S△ADF，‎ ‎∴四边形AECF是边长为5的正方形，‎ ‎∴S四边形ABCD=S正方形AECF=52=25．‎ 故答案为25．‎ ‎　‎ ‎18．（3分）在平面直角坐标系中，O为原点，⊙O的半径为7，直线y=mx﹣3m+4交⊙O于A、B两点，则线段AB的最小值为　4　．‎ ‎【解答】解：∵直线y=mx﹣3m+4必过点D（3，4），‎ ‎∴最短的弦AB是过点D且与该圆直径垂直的弦，‎ ‎∵点D的坐标是（3，4），‎ ‎∴OD=5，‎ ‎∵⊙O的半径为7，‎ ‎∴C（7，0），‎ ‎∴OA=OC=7，‎ ‎∴AD===2‎ ‎∴AB的长的最小值为4，‎ 故答案为：4．‎ ‎　‎ 三、解答题（共46分）‎ ‎19．（6分）解方程： =1﹣．‎ ‎【解答】解：去分母得：2x=x﹣2+1，‎ 移项合并得：x=﹣1，‎ 经检验x=﹣1是分式方程的解．‎ ‎　‎ ‎20．（6分）如图，有一个可以自由转动的转盘被平均分成3个扇 形，分别标有1、2、3三个数字，小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束得到一组数（若指针指在分界线时重转）．‎ ‎（1）请你用树状图或列表的方法表示出每次游戏可能出现的所有结果；‎ ‎（2）求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率．‎ ‎【解答】解：（1）列表如下：‎ ‎1‎ ‎2‎ ‎3‎ ‎1‎ ‎（1，1）‎ ‎（2，1）‎ ‎（3，1）‎ ‎2‎ ‎（1，2）‎ ‎（2，2）‎ ‎（3，2）‎ ‎3‎ ‎（1，3）‎ ‎（2，3）‎ ‎（3，3）‎ ‎（2）所有等可能的情况数为9种，其中是x2﹣3x+2=0的解的为（1，2），（2，1）共2种，‎ 则P是方程解=．‎ ‎　‎ ‎21．（6分）某商店在销售中发现：“米奇”牌童装平均每天可售出20件，每件赢利40元．为了迎“六一”儿童节，商场决定适当地降价，以扩大销售量，增加盈利，减少库存．经市场调查发现，如果每件童装每降价4元，那么平均每天就可多售出8件，要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少元？‎ ‎【解答】解：设每件童装应降价x元，根据题意列方程得，‎ ‎（40﹣x）（20+2x）=1200，‎ 解得x1=20，x2=10‎ ‎∵增加盈利，减少库存，‎ ‎∴x=10（舍去），‎ 答：每件童装降价20元．‎ ‎　‎ ‎22．（7分）如图，方格纸中每个小正方形的边长都是1个单位长度，△ABC在平面直角坐标系中的位置如图所示．[来源:学。科。网Z。X。X。K]‎ ‎（1）将△ABC向上平移3个单位后，得到△A1B1C1，请画出△A1B1C1，并直接写出点A1的坐标．‎ ‎（2）将△ABC绕点O顺时针旋转90°，请画出旋转后的△A2B2C2，并求点B所经过的路径长（结果保留x）‎ ‎【解答】解：（1）如图所示：‎ A1的坐标为：（﹣3，6）；‎ ‎（2）如图所示：‎ ‎∵BO==，‎ ‎∴==π．‎ ‎　‎ ‎23．（6分）已知关于x的一元二次方程x2﹣（2k+1）x+4k﹣3=0．‎ ‎（1）求证：无论k取什么实数值，该方程总有两个不相等的实数根；‎ ‎（2）当Rt△ABC的斜边长a为，且两条直角边的长b和c恰好是这个方程的两个根时，求△ABC的周长．‎ ‎【解答】（1）证明：△=[﹣（2k+1）]2﹣4（4k﹣3）=4k2﹣12k+13=（2k﹣3）2+4．‎ ‎∵（2k﹣3）2≥0，‎ ‎∴（2k﹣3）2+4＞0，即△＞0，‎ ‎∴无论k取什么实数值，该方程总有两个不相等的实数根；‎ ‎（2）解：∵b、c是方程x2﹣（2k+1）x+4k﹣3=0的两个根，‎ ‎∴b+c=2k+1，bc=4k﹣3．‎ ‎∵a2=b2+c2，a=，‎ ‎∴k2﹣k﹣6=0，‎ ‎∴k1=3，k2=﹣2．‎ ‎∵b、c均为正数，‎ ‎∴4k﹣3＞0，‎ ‎∴k=3，此时原方程为x2﹣7x+9=0，‎ ‎∴b+c=7，‎ ‎∴△ABC的周长为7+．‎ ‎　‎ ‎24．（6分）如图，△ABC内接于半圆，AB为直径，过点A作直线MN，若∠MAC=∠ABC ‎（1）求证：MN是该圆的切线 ‎（2）设D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F，求证：FD=FG．‎ ‎【解答】证明：（1）∵AB为直径，‎ ‎∴∠ACB=90°，‎ ‎∴∠ABC+∠CAB=90°，‎ 而∠MAC=∠ABC，‎ ‎∴∠MAC+∠CAB=90°，即∠MAB=90°，‎ ‎∴MN是半圆的切线；‎ ‎（2）如图 ‎∵AB为直径，‎ ‎∴∠ACB=90°，‎ 而DE⊥AB，‎ ‎∴∠DEB=90°，‎ ‎∴∠1+∠5=90°，∠3+∠4=90°，‎ ‎∵D是弧AC的中点，即弧CD=弧DA，‎ ‎∴∠3=∠5，‎ ‎∴∠1=∠4，‎ 而∠2=∠4，‎ ‎∴∠1=∠2，‎ ‎∴FD=FG．‎ ‎　‎ ‎25．（9分）已知二次函数y=x2﹣2mx+m2﹣1．‎ ‎（1）当二次函数的图象经过坐标原点O（0，0）时，求二次函数的解析式；‎ ‎（2）如图，当m=2时，该抛物线与y轴交于点C，顶点为D，求C、D两点的坐标；‎ ‎（3）在（2）的条件下，x轴上是否存在一点P，使得PC+PD最短？若P点存在，求出P点的坐标；若P点不存在，请说明理由．‎ ‎【解答】解：（1）∵二次函数的图象经过坐标原点O（0，0），‎ ‎∴代入二次函数y=x2﹣2mx+m2﹣1，得出：m2﹣1=0，‎ 解得：m=±1，‎ ‎∴二次函数的解析式为：y=x2﹣2x或y=x2+2x；‎ ‎（2）∵m=2，‎ ‎∴二次函数y=x2﹣2mx+m2﹣1得：y=x2﹣4x+3=（x﹣2）2﹣1，‎ ‎∴抛物线的顶点为：D（2，﹣1），‎ 当x=0时，y=3，‎ ‎∴C点坐标为：（0，3），‎ ‎∴C（0，3）、D（2，﹣1）；‎ ‎（3）当P、C、D共线时PC+PD最短，‎ 过点D作DE⊥y轴于点E，‎ ‎∵PO∥DE，‎ ‎∴=，‎ ‎∴=，‎ 解得：PO=，‎ ‎∴PC+PD最短时，P点的坐标为：P（，0）．‎ ‎　‎