2019九年级数学上册 专题突破讲练 解决方位角问题试题 （新版）青岛版 11页

解决方位角问题 方位角 方位角：指北（或指南）方向线与目标方向线所成的小于90°的角叫做方位角。如图中的目标方向线OA、OB、OC分别表示北偏东60°，南偏东30°，北偏西70°。特别地，若目标方向线与指北（或指南）的方向线成45°的角，如图的目标方向线OD与正南方向线成45°角，通常称为西南方向。‎ 方法归纳：方位角可以看成是将正北或正南方向的射线旋转一定角度而形成的。故在应用中，一要确定其始边是正北还是正南；二要确定其旋转方向是向东还是向西；三要确定旋转角度的大小。‎ 总结：‎ ‎1. 能够根据题意作出方位角，分清图形中的方位角。‎ ‎2. 合理构造直角三角形，会解与方位角有关的三角函数问题。‎ 例题 据气象台预报，一强台风的中心位于A市的东南方向（36＋108）km的海面上P处。目前台风中心以‎20km/h的速度向北偏西60°的方向移动，距台风中心‎50km的圆形区域均会受到强袭击。已知B市位于A市的正南方向‎72km处，C市位于B市的北偏东60°方向‎56km处。那么，会受到这次强台风袭击的城市是（ ）‎ A. 只有A市 B. 只有B市 C. B市和C市 D. A市、B市和C市 解析：‎ 11‎ 分别过点A、B、C构造直角三角形，计算点A、B、C到直线PQ的距离，比较它们与50的大小关系即可。‎ 答案：如图，过P作PO⊥AB于O。∠OAP＝∠APO＝45°。∴OA＝OP＝APsin45°＝（36＋108）×＝（36＋108）。BO＝AO－AB＝36＋108－72＝（36＋36）。设台风方向PQ与AO交点为M，∠MPO＝90°－60°＝30°，OM＝OPtan30°＝（36＋108）×＝（36＋36）。∴OM＝OB，∴点M和B重合，∴台风中心必经过B市。过C作CD⊥PQ于D，∠CBD＝90°－60°＋30°＝60°，CD＝CBsin60°＝56×＝28＜50，∴C市也受台风影响。过点A作AG⊥PQ于点G，AG＝ABsin60°＝72×＝36＞50，∴A市不受台风袭击。选C。‎ 点拨：解答这类问题时必须要明确两点，一是台风行进的路线，二是某点到台风行进路线的距离。所以，其解题思路一般都是围绕某条直线和某些点构造直角三角形，运用三角函数及勾股定理求解。‎ 解答方位角问题一定要结合图形，只要确定了方向线与南北方向线的夹角，就可解决问题。但关键还是构造直角三角形，将方位角转化为直角三角形的内角。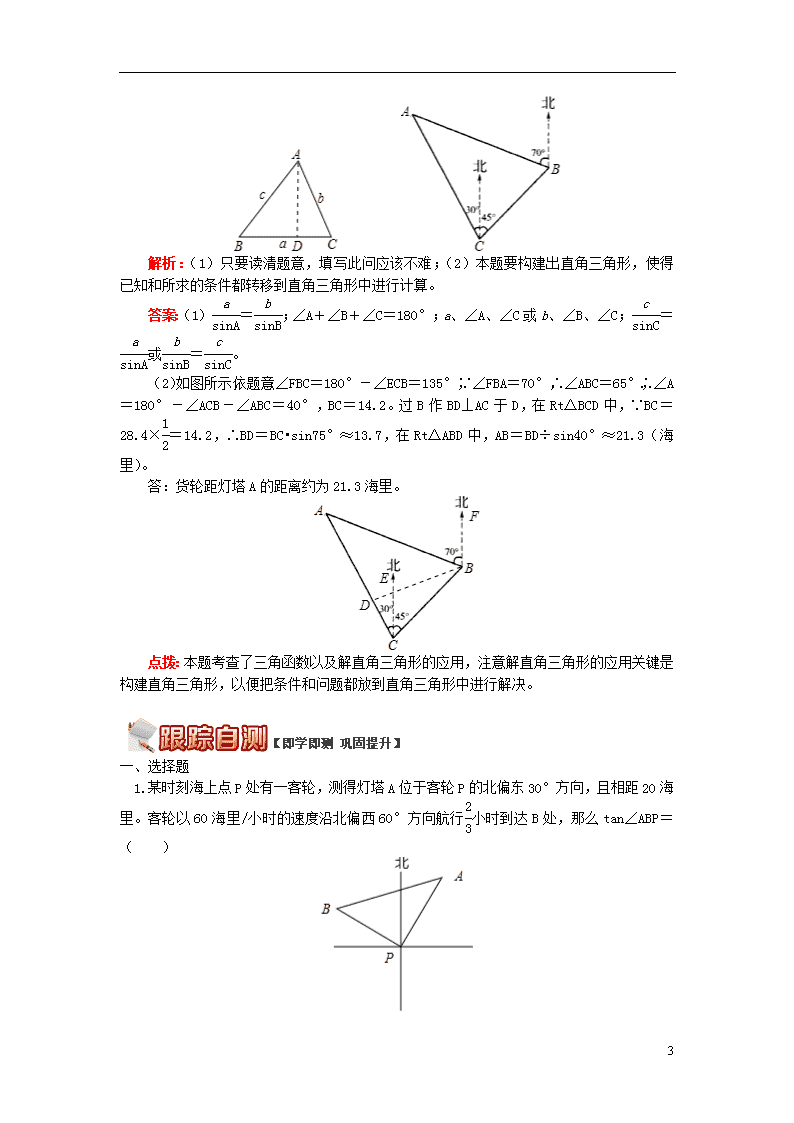‎ 满分训练 阅读下列材料，并解决后面的问题。‎ 在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c。过A作AD⊥BC于D（如图），则sinB＝，sinC＝，即AD＝csinB，AD＝bsinC，于是csinB＝bsinC，即＝。同理有＝，所以＝＝。即：在一个三角形中，各边和它所对角的正弦的比相等。‎ ‎（1）在锐角三角形中，若已知三个元素a、b、∠A，运用上述结论和有关定理就可以求出其余三个未知元素c、∠B、∠C，请你按照下列步骤填空，完成求解过程：‎ 第一步：由条件a、b、∠A，用关系式__________求出∠B；‎ 第二步：由条件∠A、∠B，用关系式__________求出∠C；‎ 第三步：由条件__________，用关系式__________求出c。‎ ‎（2）一艘货轮在C处测得灯塔A在货轮的北偏西30°的方向上，随后货轮以‎28.4海里/时的速度按北偏东45°的方向航行，半小时后到达B处，此时又测得灯塔A在货轮的北偏西70°的方向上（如图），求此时货轮距灯塔A的距离AB（结果精确到0.1，参考数据：sin40°＝0.643，sin65°＝0.906，sin70°＝0.940，sin75°＝0.966）。‎ 11‎ ‎ ‎ 解析：（1）只要读清题意，填写此问应该不难；（2）本题要构建出直角三角形，使得已知和所求的条件都转移到直角三角形中进行计算。‎ 答案：（1）＝；∠A＋∠B＋∠C＝180°；a、∠A、∠C或b、∠B、∠C；＝或＝。‎ ‎（2）如图所示，依题意：∠FBC＝180°－∠ECB＝135°，∵∠FBA＝70°，∴∠ABC＝65°，∴∠A＝180°－∠ACB－∠ABC＝40°，BC＝14.2。过B作BD⊥AC于D，在Rt△BCD中，∵BC＝28.4×＝14.2，∴BD＝BC•sin75°≈13.7，在Rt△ABD中，AB＝BD÷sin40°≈21.3（海里）。‎ 答：货轮距灯塔A的距离约为‎21.3海里。‎ 点拨：本题考查了三角函数以及解直角三角形的应用，注意解直角三角形的应用关键是构建直角三角形，以便把条件和问题都放到直角三角形中进行解决。‎ 一、选择题 ‎1. 某时刻海上点P处有一客轮，测得灯塔A位于客轮P的北偏东30°方向，且相距20海里。客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处，那么tan∠ABP＝（ ）‎ 11‎ A. B. ‎2 ‎C. D. ‎2. 如图，学校在小明家北偏西30°方向，且距小明家‎6千米，那么学校所在位置A点坐标为（ ）‎ A. （3，3） B. （－3，－3）‎ C. （3，－3） D. （－3，3）‎ ‎*3. 如图，某天然气公司的主输气管道从A市的北偏东60°方向直线延伸，测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向，测绘员沿主输气管道步行‎1000米到达点C处，测得M小区位于点C的北偏西75°方向，试在主输气管道上寻找支管道连接点N，使到该小区铺设的管道最短，此时AN的长约是（ ）米 A. 366 B. ‎650 ‎ C. 634 D. 700‎ ‎**4. 一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西80°方向向海岛C靠近，同时，从A处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C处恰好追上渔船，那么救援船航行的速度为（ ）‎ A. 10海里/小时 B. 30海里/小时 ‎ C. 20海里/小时 D. 30海里/小时 二、填空题 ‎5. ‎ 11‎ 如图，一天，我国一渔政船航行到A处时，发现正东方向的我领海区域B处有一可疑渔船，正在以16海里/小时的速度向西北方向航行，我渔政船立即沿北偏东60°方向航行，1.5小时后，在我领海区域的C处截获可疑渔船。我渔政船的航行路程是__________海里。 ‎ ‎6. 如图，在港口M的南偏西60°方向有一座小岛P，一船以每小时20千米的速度从港口M出发，沿正西方向行驶，半个小时后，这艘船在A处测得小岛在船的正南方向，那么小岛P与港口M相距__________千米。 ‎ ‎7. 如图，A、B两地之间有一座山，汽车原来从A地到B地经过C地沿折线A→C→B行驶，现开通隧道后，汽车直接沿直线AB行驶。已知AC＝10千米，∠A＝30°，∠B＝45°。则隧道开通后，汽车从A地到B地比原来少走__________千米。（结果保留根号）‎ ‎*8. 如图，某海监船向正西方向航行，在A处望见一艘正在作业的渔船D在南偏西45°方向，海监船航行到B处时望见渔船D在南偏东45°方向，又航行了半小时到达C处，望见渔船D在南偏东60°方向，若海监船的速度为50海里/小时，则A，B之间的距离为__________海里（取≈1.7，结果精确到0.1海里）。‎ 三、解答题 ‎9. 如图，益阳市梓山湖中有一孤立小岛，湖边有一条笔直的观光小道AB，现决定从小岛架一座与观光小道垂直的小桥PD，小张在小道上测得如下数据：AB＝‎80.0米，∠PAB＝38.5°，∠PBA＝26.5°。请帮助小张求出小桥PD的长并确定小桥在小道上的位置。（以A，B为参照点，结果精确到‎0.1米）（参考数据：sin38.5°＝0.62，cos38.5°＝0.78，tan38.5°＝0.80，sin26.5°＝0.45，cos26.5°＝0.89，tan26.5°＝0.50）‎ 11‎ ‎10. 2013年3月，某煤矿发生瓦斯爆炸，该地救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象。已知A、B两点相距‎4米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度。（精确到‎0.1米，参考数据：≈1.41，≈1.73）‎ ‎*11. 如图，马路的两边CF、DE互相平行，线段CD为人行横道，马路两侧的A、B两点分别表示车站和超市。CD与AB所在直线互相平行，且都与马路两边垂直，马路宽‎20米，A，B相距‎62米，∠A＝67°，∠B＝37°。‎ ‎（1）求CD与AB之间的距离；‎ ‎（2）某人从车站A出发，沿折线A→D→C→B去超市B，求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米？（参考数据：sin67°≈，cos67°≈，tan67°≈，sin37°≈，cos37°≈，tan37°≈）‎ ‎**12. 机器人“海宝”在某圆形区域表演“按指令行走”，如图所示，“海宝”从圆心O出发，先沿北偏西67.4°方向行走‎13米至点A处，再沿正南方向行走‎14米至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上。（本题参考数据：sin67.4°＝，cos67.4°＝，tan67.4°＝）‎ 11‎ ‎（1）求弦BC的长；‎ ‎（2）求圆O的半径长。‎ 11‎ ‎1. A 解析：∵灯塔A位于客轮P的北偏东30°方向，且相距20海里。∴PA＝20，∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处，∴∠APB＝90°，BP＝60×＝40，∴tan∠ABP＝＝＝。‎ ‎2. D 解析：∵学校在小明家北偏西30°方向，且距小明家‎6千米，∴∠BOA＝30°，OA＝6。‎ ‎∵∠ABO＝90°，∴AB＝3，OB＝OAcos30°＝3。即A点坐标为（－3，3）。‎ ‎3. C 解析：如图：过点M作MN⊥AC于点N，根据题意得：∠MAN＝60°－30°＝30°，∠BCM＝75°，∠DCA＝60°，∴∠MCN＝180°－75°－60°＝45°，设MN＝x米，在Rt△AMN中，AN＝＝x（米），在Rt△CMN中，CN＝＝x（米），∵AC＝‎1000米，∴x＋x＝1000，解得：x＝500（－1），∴AN＝x≈634（米）。‎ ‎4. D 解析：如图，过点C作CD⊥AB于D。设AC＝x海里。在△ACD中，∠ADC＝90°，∠CAD＝10°＋20°＝30°，∴CD＝ACsin∠CAD＝AC＝x海里，AD＝ACcos∠CAD＝x海里。在△BCD中，∠BDC＝90°，∠CBD＝80°－20°＝60°，∴BD＝＝x海里。‎ ‎∵AD＋BD＝AB，∴x＋x＝20，解得x＝10（海里），∴救援船航行的速度为：10÷＝30（海里/小时）。‎ 11‎ ‎5. 24 解析：如图，作CD⊥AB于点D，垂足为D，∵在直角三角形BCD中，BC＝16×1.5＝24（海里），∠CBD＝45°，∴CD＝BC•sin45°＝24×＝12（海里），∴在直角三角形ACD中，AC＝＝12×2＝24（海里）。‎ ‎6. 解析：在直角△APM中，AM＝20×＝10千米，∠P＝60°，则PM＝＝（千米）。‎ ‎7. 5＋5－5 解析：过C作CD⊥AB于D，在Rt△ACD中，∵AC＝10，∠A＝30°，∴DC＝ACsin30°＝5，AD＝ACcos30°＝5，在Rt△BCD中，∵∠B＝45°，∴BD＝CD＝5，BC＝5，则用AC＋BC－（AD＋BD）＝10＋5－（5＋5）＝5＋5－5（千米）。‎ ‎8. 67.5 解析：∵∠DBA＝∠DAB＝45°，∴△DAB是等腰直角三角形，过点D作DE⊥AB于点E，则DE＝AB，设DE＝x，则AB＝2x，在Rt△CDE中，∠DCE＝30°，则CE＝DE＝x，在Rt△BDE中，∠DAE＝45°，则DE＝BE＝x，由题意得，CB＝CE－BE＝x－x＝50×，解得：x＝，故AB＝25（＋1）＝67.5（海里）。‎ 11‎ ‎9. 解：设PD＝x米，∵PD⊥AB，∴∠ADP＝∠BDP＝90°，在Rt△PAD中，tan∠PAD＝，∴AD＝≈＝x，在Rt△PBD中，tan∠PBD＝，∴DB＝≈＝2x，又∵AB＝‎80.0米，∴x＋2x＝80.0，解得：x≈24.6，即PD≈‎24.6米，∴DB＝2x＝49.2。‎ 答：小桥PD的长度约为‎24.6米，位于AB之间距B点约‎49.2米处。‎ ‎10. 解：过点C作CD⊥AB于点D，设CD＝x，在Rt△ACD中，∠CAD＝30°，则AD＝CD＝x，在Rt△BCD中，∠CBD＝45°，则BD＝CD＝x，由题意得，x－x＝4，解得：x＝＝2（＋1）≈5.5。答：生命所在点C的深度为‎5.5米。‎ ‎11. 解：（1）设CD与AB之间的距离为x，则在Rt△BCF和Rt△ADE中，＝tan37°，＝tan67°，∴BF＝＝x，AE＝＝x，又∵AB＝62，CD＝20，∴x＋x＋20＝62，解得x＝24，故CD与AB之间的距离为‎24米；‎ ‎（2）在Rt△BCF和Rt△ADE中，∵BC＝＝24×＝40，AD＝＝＝26，‎ ‎∴AD＋DC＋CB－AB＝40＋20＋26－62＝24（米）。‎ 答：他沿折线A→D→C→B到达超市比直接横穿马路多走‎24米。‎ ‎12. 解：（1）连接OB，过点O作OD⊥AB，∵AB∥SN，∠AON＝67.4°，∴∠A＝67.4°。∴OD＝AO•sin67.4°＝13×＝12。又∵BE＝OD，∴BE＝12。根据垂径定理，BC＝2×12＝24（米）‎ ‎（2）∵AD＝AO•cos67.4°＝13×＝5，∴OD＝＝12，BD＝AB－AD＝14－5＝9。∴BO＝＝15。故圆O的半径长‎15米。‎ 11‎ 11‎