2014年江西省抚州市中考数学试题（含答案） 14页

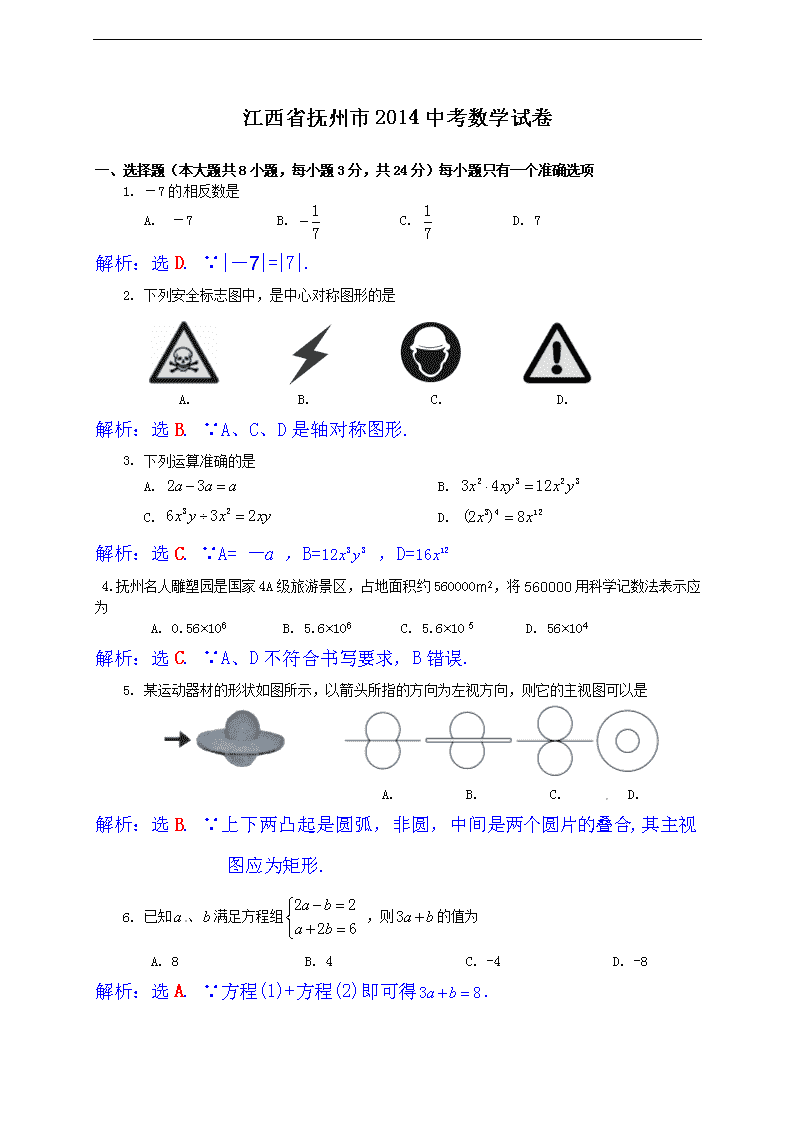
江西省抚州市2014中考数学试卷 一、选择题（本大题共8小题，每小题3分，共24分）每小题只有一个准确选项 ‎ 1. －7的相反数是 ‎ A. －7 B. C. D. 7 ‎ 解析：选D. ∵|－7|=|7|.‎ ‎2. 下列安全标志图中，是中心对称图形的是 ‎ ‎ ‎ ‎ ‎ A. B. C. D.‎ 解析：选B. ∵A、C、D是轴对称图形.‎ ‎3. 下列运算准确的是 ‎ A. B.‎ ‎ C. D.‎ 解析：选C. ∵A= －a ，B= ，D=‎ ‎ 4. 抚州名人雕塑园是国家4A级旅游景区，占地面积约560000m2，将560000用科学记数法表示应为 ‎ A. 0.56×106 B. 5.6×106 C. 5.6×10 5 D. 56×104‎ 解析：选C. ∵A、D不符合书写要求，B错误.‎ ‎5. 某运动器材的形状如图所示，以箭头所指的方向为左视方向，则它的主视图可以是 ‎ ‎ ‎ A. B. C. D.‎ 解析：选B. ∵上下两凸起是圆弧，非圆，中间是两个圆片的叠合,其主视图应为矩形.‎ 6. 已知、满足方程组 ，则的值为 ‎ A. 8 B. 4 C. -4 D. -8‎ 解析：选A. 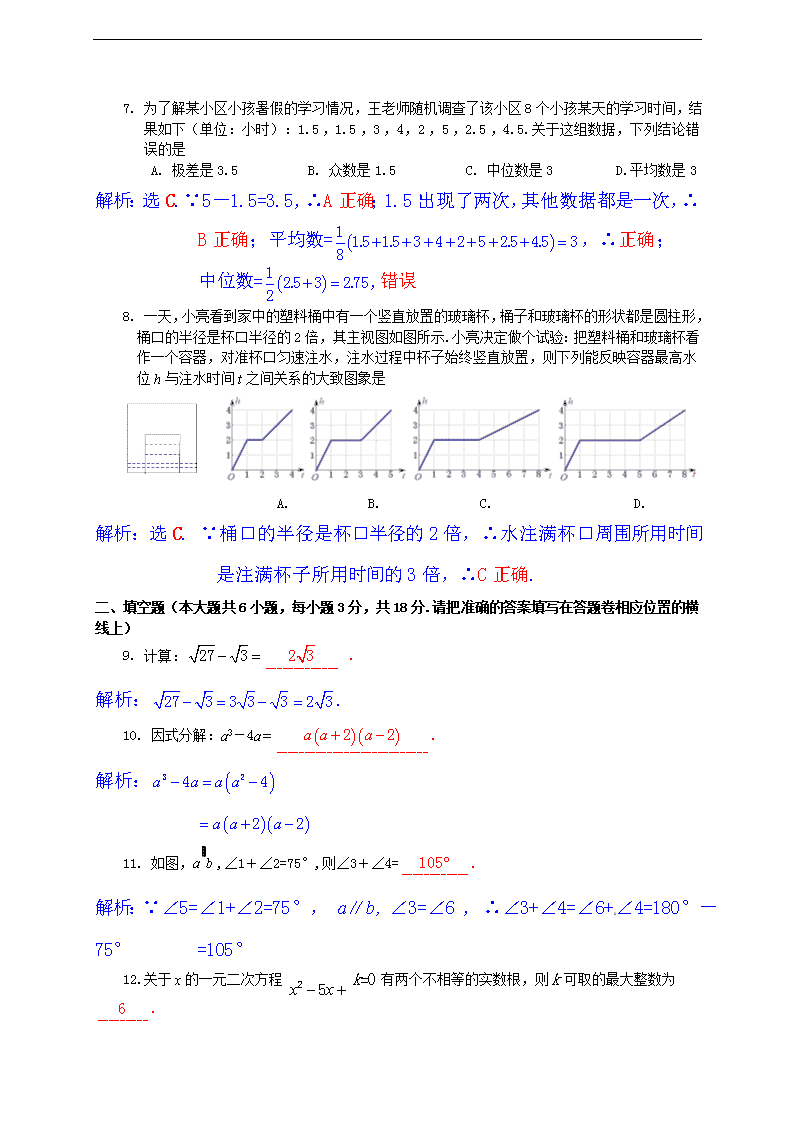∵方程(1)+方程(2)即可得.‎ ‎7. 为了解某小区小孩暑假的学习情况，王老师随机调查了该小区8个小孩某天的学习时间，结果如下（单位：小时）：1.5 ，1.5 ，3 ，4，2 ，5 ，2.5 ，4.5.关于这组数据，下列结论错误的是[来源:学§科§网Z§X§X§K]‎ ‎ A. 极差是3.5 B. 众数是1.5 C. 中位数是3 D.平均数是3‎ 解析：选C. ∵5－1.5=3.5 ,∴A正确；1.5出现了两次，其他数据都是一次，∴B正确；平均数=，∴正确；‎ ‎ 中位数=,错误 ‎8. 一天，小亮看到家中的塑料桶中有一个竖直放置的玻璃杯，桶子和玻璃杯的形状都是圆柱形，桶口的半径是杯口半径的2倍，其主视图如图所示.小亮决定做个试验：把塑料桶和玻璃杯看作一个容器，对准杯口匀速注水，注水过程中杯子始终竖直放置，则下列能反映容器最高水位h与注水时间t之间关系的大致图象是 ‎ A. B. C. D.‎ 解析：选C. ∵桶口的半径是杯口半径的2倍，∴水注满杯口周围所用时间是注满杯子所用时间的3倍，∴C正确.‎ 二、填空题（本大题共6小题，每小题3分，共18分.请把准确的答案填写在答题卷相应位置的横线上）‎ ‎9. 计算： .‎ 解析：.‎ ‎10. 因式分解：a3－4a.‎ 解析：‎ ‎ ‎ ‎11. 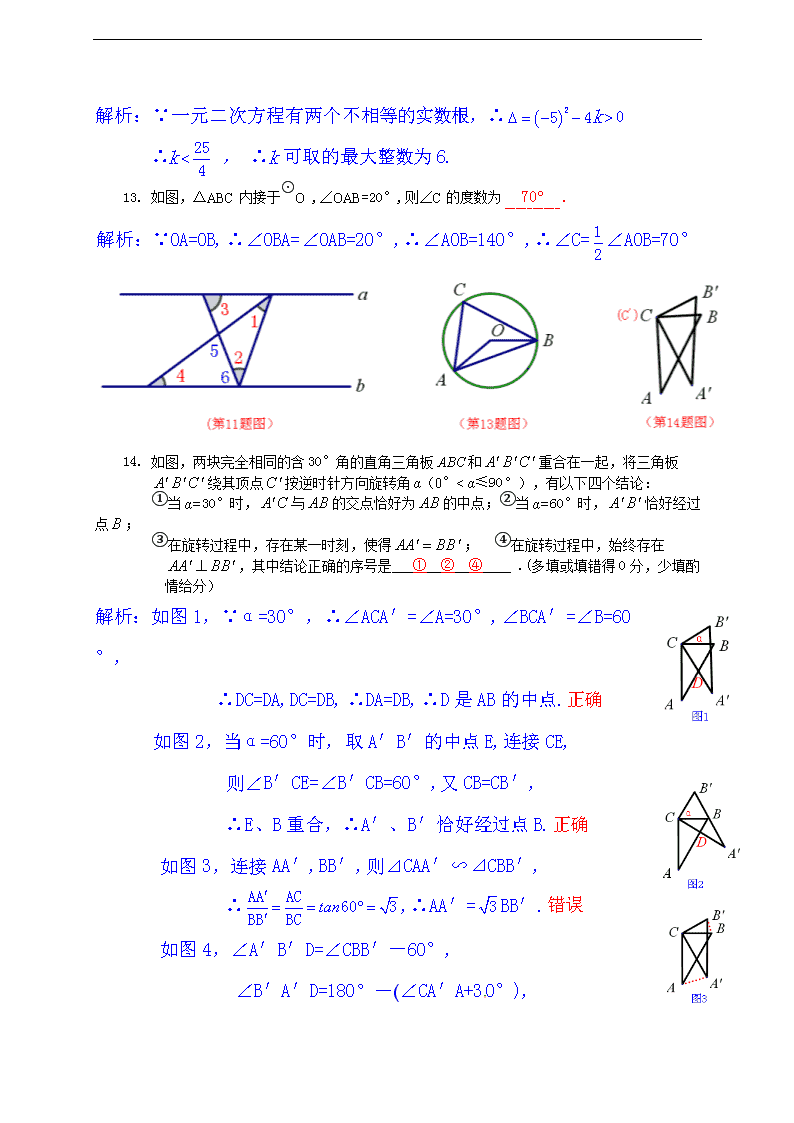如图，a∥b ,∠1＋∠2=75°,则∠3＋∠4=.‎ 解析：∵∠5=∠1+∠2=75°， a∥b, ∠3=∠6 , ∴∠3+∠4=∠6+∠4=180°－75° =105°‎ ‎ 12.关于x的一元二次方程 k=0有两个不相等的实数根，则k可取的最大整数为.‎ 解析：∵一元二次方程有两个不相等的实数根，∴k ‎ ∴k ， ∴k可取的最大整数为6.‎ ‎ 13. 如图，△ABC内接于⊙O ,∠OAB=20°,则∠C的度数为.‎ 解析：∵OA=OB,∴∠OBA=∠OAB=20°,∴∠AOB=140°,∴∠C=∠AOB=70° ‎ ‎14. 如图，两块完全相同的含30°角的直角三角板ABC和重合在一起，将三角板绕其顶点按逆时针方向旋转角α（0°< α≤90°），有以下四个结论：‎ ‎ ①当α=30°时，与的交点恰好为的中点；②当α=60°时，恰好经过点；‎ ‎ ③在旋转过程中，存在某一时刻，使得； ④在旋转过程中，始终存在，其中结论正确的序号是 ① ② ④ .(多填或填错得0分，少填酌情给分）‎ 解析：如图1，∵α=30°，∴∠ACA′=∠A=30°,∠BCA′=∠B=60°，‎ ‎ ∴DC=DA,DC=DB,∴DA=DB,∴D是AB的中点.正确 ‎ ‎ 如图2，当α=60°时，取A′B′的中点E,连接CE,‎ ‎ 则∠B′CE=∠B′CB=60°,又CB=CB′,‎ ‎ ∴E、B重合，∴A′、B′恰好经过点B.正确 ‎ 如图3，连接AA′,BB′,则⊿CAA′∽⊿CBB′,‎ ‎ ∴,∴AA′=BB′.错误 ‎ 如图4，∠A′B′D=∠CBB′－60°,‎ ‎ ∠B′A′D=180°－(∠CA′A+30°),‎ ‎ ∴∠A′B′D＋∠B′A′D=90°＋∠CBB′－∠CA′A ‎ ∵ ∠CBB′=∠CA′A , ‎ ‎ ∴∠A′B′D＋∠B′A′D=90°,即∠D=90°,‎ ‎ ∴AA′⊥BB′.正确 ‎ ∴①，②，④正确.‎ 三、（本大题共2小题，每小题5分，共10分）‎ ‎15. 如图，△与△关于直线对称，请用无刻度的直尺，在下面两个图中分别作出直线.‎ 解析：利用轴对称性质：对应线段（或延 ‎ 长线）的交于对称轴上一点. ‎ ‎ 如图 ，直线l 就是所求作的对称轴. ‎ ‎16. 先化简： ，再任选一个你喜欢的数代入求值.‎ 解析：原式= 取 代入， ‎ ‎ = 原式=8 ‎ ‎ == (注：不能取1和2）‎ 四、（本大题共2小题，每小题7分，共14分）‎ ‎ 17. 某同学报名参加运动会，有以下5个项目可供选择：‎ ‎ 径赛项目：100m ,200m ,400m(分别用A1 、A2 、A3表示）；‎ ‎ 田赛项目：跳远 ，跳高（分别用B1 、B2表示）.‎ ‎ ⑴ 该同学从5个项目中任选一个，恰好是田赛项目的概率为 ；‎ ‎ ⑵ 该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率.‎ 解析：(1)∵5个项目中有2个田赛项目，∴P田赛=‎ A1‎ A2‎ A3‎ B1‎ B2‎ A1‎ ‎(A1，A2)‎ ‎(A1,，A3)‎ ‎(A1,B1)‎ ‎(A1,B2)‎ A2‎ ‎(A2,A1)‎ ‎(A1,，A3)‎ ‎(A2,B1)‎ ‎(A2,B2)‎ A3[来源:学科网]‎ ‎(A3,A1)‎ ‎(A3，A2)‎ ‎(A3,B1)‎ ‎(A3,B2)‎ B1‎ ‎(B1,A1)‎ ‎(B1，A2)‎ ‎(B1,，A3)‎ ‎(B1,B2)‎ B2‎ ‎(B2,A1)‎ ‎(B2，A2)‎ ‎(B2,，A3)‎ ‎(B2,B1)‎ ‎ (2)‎ ‎ ‎ ‎ ∴共20种可能的结果，符合条件的有12种，‎ ‎ ∴P(田，径)=.‎ ‎18. 如图，在平面直角坐标系中，过点的直线与轴平行，且直线分别与反比例函数 和 的图象交于点、点.‎ ‎ ⑴ 求点的坐标；‎ ‎ ⑵ 若△的面积为8 ，求k的值 . ‎ 解析：(1)∵PQ∥轴，∴P点纵坐标为2，‎ ‎ 当时， ， ‎ ‎ ∴ ， ∴P(3，2).‎ ‎ (2)∵S⊿POQ=, ∴ , ‎ ‎ ∴PQ=8, ∵PM=3, ∴QM=5,‎ ‎ ∴Q(－5,2) , 代入 得： ‎ 五、（本大题共2小题，每小题8分，共16分）‎ ‎ 19. 情景：‎ ‎ 试根据图中的信息，解答下列问题：‎ ‎ ⑴ 购买6根跳绳需 元，购买12根跳绳需 元.‎ ‎ ⑵ 小红比小明多买2根，付款时小红反而比小明少5元，你认为有这种可能吗？若有，请求出小红购买跳绳的根数；若没有，请说明理由.‎ 解析：(1)25×6=150, 25×0.8×12=240.‎ ‎ (2)有这种可能.‎ ‎ 设小红买了根跳绳，‎ ‎ 则25×0.8·=25(－2)-5 ,解得=11.‎ ‎ ∴小红买了11根跳绳.‎ ‎20. 某校举行“汉字听写”比赛，每位学生听写汉字39个，比赛结束后随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图的一部分.‎ 组别 听写正确的 个数x 组中值 A ‎0≤x<8‎ ‎4‎ B ‎8≤x<16‎ ‎12‎ C ‎16≤x<24‎ ‎20‎ D ‎24≤x<32‎ ‎28‎ E ‎32≤x<40‎ ‎36‎ ‎ ‎ ‎[来源:学科网]‎ ‎ ‎ 根据以上信息解决下列问题：‎ ⑴ 本次共随机抽查了100名学生，并补全条形统计图；‎ ⑵ 若把每组听写正确的个数用这组数据的组中值代替，则被抽查学生听写正确的个数的平均数是多少？‎ ⑶ 该校共有3000名学生，如果听写正确的个数少于24个定为不合格，请你估计这所学校本次比赛听写不合格的学生人数.‎ 解析：(1)15÷15%=100. ∴共抽查了100名学生；‎ ‎ 补全条形统计图如上.‎ ‎ (2)4×10%＋12×15%＋20×25%＋28×30%＋36×20%=22.8,‎ ‎ ∴被抽查学生听写正确的个数的平均数是22.8个；‎ ‎ (3)(10%＋15%＋25%)×3000=1500,‎ ‎ ∴这所学校本次比赛听写不合格的学生人数约1500名.‎ 六、（本大题共2小题，每小题9分，共18分）‎ ‎21. 如图1所示的晾衣架，支架主视图的基本图形是菱形，其示意图如图2.晾衣架伸缩时，点在射线 上滑动，∠的大小也随之发生变化.已知每个菱形边长均等于20cm ,且 图1‎ 图2‎ ‎ =20cm .‎ ‎ ‎ ‎ ⑴ 当∠=60°时，求两点间的距离；‎ ‎ ⑵ 当∠由60°变为120°时，点向左移动了多少cm ?(结果精确到0.1cm)‎ ‎ ⑶ 设cm ,当∠的变化范围为60°~ 120°(包括端点值)时，求的取值范围 .(结果精确到0.1cm) (参考数据 ，可使用科学计算器)‎ 解析：(1)如图1，∵每个菱形的边长都是20㎝，‎ ‎ 且DE=20㎝, ∴CE=DE,‎ ‎ ∵∠CED=60°，‎ ‎ ∴⊿CED是等边三角形，‎ ‎ ∴CD=20cm, ∴C、D两点之间的距离是20cm.‎ ‎ (2)如图2，作EH⊥CD于H,‎ ‎ 在⊿CED中，CE=DE，‎ ‎ ∠CED=120°‎ ‎ ∴∠ECD=30°,∴EH=CE=10,‎ ‎ ∴CH=10 , ∴CD=20, ‎ ‎∴点C向左移动了(20－20),‎ ‎ ∴点A向左移动了(20－20)×3≈43.9cm .‎ ‎ (3)如图1，当∠CED=60°时， ∵ED=EG, ∠CGD=30°，‎ ‎ 在Rt⊿CGD中， ，∵CG=40,‎ ‎ ∴DG=20≈34.6；‎ ‎ 如图2，当∠CED=120°时， ∠CGD=60°,‎ ‎ ∴DG=CG=20, ∴20≤≤34.6.‎ ‎22. 如图，在平面直角坐标系中，⊙经过轴上一点，与y轴分别交于、两点，连接并延长分别交⊙、轴于点、，连接并延长交y轴于点，若点的坐标为(0 ,1),点的坐标为(6 ,－1).‎ ‎ ⑴ 求证：‎ ‎ ⑵ 判断⊙与轴的位置关系，并说明理由.‎ ‎ ⑶ 求直线的解析式.‎ ‎ ‎ 解析：(1)如图1，作DH⊥轴于点H,‎ ‎ ∵F(0,1),D(6,-1)‎ ‎ ∴OF=DH=1,‎ ‎ 在⊿OCF和⊿HCD中，‎ ‎ ‎ ‎ ∴⊿OCF≌⊿HCD(AAS), DC=FC.‎ ‎ (2)如图2，⊙P与轴相切.‎ ‎ 连接PC,‎ ‎ ∵DC=FC, PD=PA,‎ ‎ ∴CP是⊿DFA的中位线，‎ ‎ ∴PC∥轴，‎ ‎ ∴PC⊥轴 , 又C是⊙P与轴的交点 ，‎ ‎ ∴⊙P切轴于点C.‎ ‎ (3)如图3，作PG⊥轴于点G,‎ ‎ 由(1)知：C(3,0),‎ ‎ 由(2)知：AF=2PC,‎ ‎ 设⊙P的半径为r ,‎ ‎ 则：（r-1)2+32=r2 , ∴r=5, ∴A(0,-9)；‎ ‎ 设直线AD的解析式为，‎ ‎ 把D(6,-1)代入得： ，‎ ‎ ∴直线AD的解析式为：‎ 七、(本大题共2小题，每小题10分，共20分)‎ ‎ 23. 如图，抛物线 ()位于轴上方的图象记为1 ，它与轴交于1 、两点，图象2与1关于原点对称， 2与轴的另一个交点为2 ，将1与2同时沿轴向右平移12的长度即可得3与4 ；再将3与4 同时沿轴向右平移12的长度即可得5与6 ； ……按这样的方式一直平移下去即可得到一系列图象1 ,2 ,…… ，n ,我们把这组图象称为“波浪抛物线”.‎ ⑴ 当时，‎ ‎ ① 求图象1的顶点坐标；‎ ‎ ② 点(2014 , －3) 不在 (填“在”或“不在”)该“波浪抛物线”上；若图象n 的顶点n的横坐标为201，则图象n 对应的解析式为 ，其自变量的取值范围为.‎ ‎ ⑵ 设图象m、m+1的顶点分别为m 、m+1 (m为正整数),轴上一点Q的坐标为(12 ,0).试探究：当为何值时，以、m 、m+1、Q四点为顶点的四边形为矩形？并直接写出此时m的值.‎ 解析：(1)当时，‎ ‎ ①，∴F1的顶点是（-1,1)；‎ ‎ ②由①知：“波浪抛物线”的值的取值范围是-1≤≤1，‎ ‎ ∴点H(2014,-3)不在“波浪抛物线”上；‎ ‎ 由平移知：F2： F3：，…，‎ ‎ ∵Fn的顶点横坐标是201，∴Fn的解析式是：，‎ ‎ 此时图象与轴的两个交点坐标是（200,0)、(202,0),‎ ‎ ∴200≤≤202 .‎ ‎ (2)如下图，取OQ的中点O′,连接Tm Tm+1 ,‎ ‎ ∵四边形OTmQTm+1是矩形，[来源:学.科.网]‎ ‎ ∴Tm Tm+1=OQ=12, 且 Tm Tm+1 经过O′, ∴OTm+1=6,‎ ‎ ∵F1：‎ ‎ ∴Tm+1的纵坐标为，‎ ‎ ∴()2+12 =62 , ∴=± ,‎ ‎ 已知＜0 ， ∴ .‎ ‎ ∴当时，以以O、Tm 、Tm+1、Q四点为顶点的四边形为矩形.‎ ‎ 此时m=4. ‎ ‎24.【试题背景】‎ 已知：∥∥∥，平行线与、与、与之间的距离分别为1、2、3，且1 =3 = 1，2 = 2 . 我们把四个顶点分别在、、、这四条平行线上的四边形称为“格线四边形”.‎ ‎ 【探究1】 ⑴ 如图1，正方形为“格线四边形”，于点,的反向延长线交直线于点. 求正方形的边长.‎ ‎ 【探究2】 ⑵ 矩形为“格线四边形”，其长 ：宽 = 2 ：1 ，则矩形的宽为. (直接写出结果即可)‎ ‎ 【探究3】 ⑶ 如图2，菱形为“格线四边形”且∠=60°，△是等边三角形， 于点， ∠=90°，直线分别交直线、于点、. 求证：.‎ ‎ 【拓 展】 ⑷ 如图3，∥，等边三角形的顶点、分别落在直线、上，于点， 且=4 ，∠=90°，直线分别交直线、于点、，点、分别是线段、上的动点，且始终保持=，于点.‎ ‎ 猜想：在什么范围内，∥？并说明此时∥的理由.‎ ‎ ‎ 解析：(1) 如图1， ∵BE⊥l , l ∥k ,‎ ‎ ∴∠AEB=∠BFC=90°, ‎ ‎ 又四边形ABCD是正方形，‎ ‎ ∴∠1+∠2=90°，AB=BC, ∵∠2+∠3=90°, ∴ ∠1=∠3,‎ ‎ ∴⊿ABE≌⊿BCF(AAS),‎ ‎ ∴AE=BF=1 , ∵BE=d1+d2=3 , ∴AB= , ‎ ‎ ∴正方形的边长是 .‎ ‎ (2)如图2,3，⊿ABE∽⊿BCF,‎ ‎ ∴ 或 ‎ ‎ ‎ ‎ ∵BF=d3=1 , ‎ ‎ ∴AE= 或 ‎ ∴AB= 或 ‎ AB=‎ ‎ ∴矩形ABCD的宽为或. (注意：要分2种情况讨论）‎ ‎ (3)如图4，连接AC，‎ ‎ ∵四边形ABCD是菱形，‎ ‎ ∴AD=DC,‎ ‎ 又∠ADC=60°, ‎ ‎ ∴⊿ADC是等边三角形，‎ ‎∴AD=AC，‎ ‎ ∵AE⊥k , ∠AFD=90°, ∴∠AEC=∠AFD=90°，‎ ‎ ∵⊿AEF是等边三角形， ∴ AF=AE,‎ ‎ ∴⊿AFD≌⊿AEC(HL), ∴EC=DF.‎ ‎ (4)如图5，当2＜DH＜4时， BC∥DE .‎ ‎ 理由如下： ‎ ‎ 连接AM,‎ ‎ ∵AB⊥k , ∠ACD=90°,‎ ‎ ∴∠ABE=∠ACD=90°,‎ ‎ ∵⊿ABC是等边三角形，‎ ‎∴AB=AC ,‎ ‎ 已知AE=AD, ∴⊿ABE≌⊿ACD(HL)，∴BE=CD；‎ ‎ 在Rt⊿ABM和Rt⊿ACM中，‎ ‎ ，∴Rt⊿ABM≌Rt⊿ACM(HL),‎ ‎ ∴ BM=CM ；‎ ‎ ∴ME=MD,‎ ‎ ∴ , ∴ED∥BC.‎