2020年河南省南阳市淅川县中考数学一模试卷 (含解析) 24页

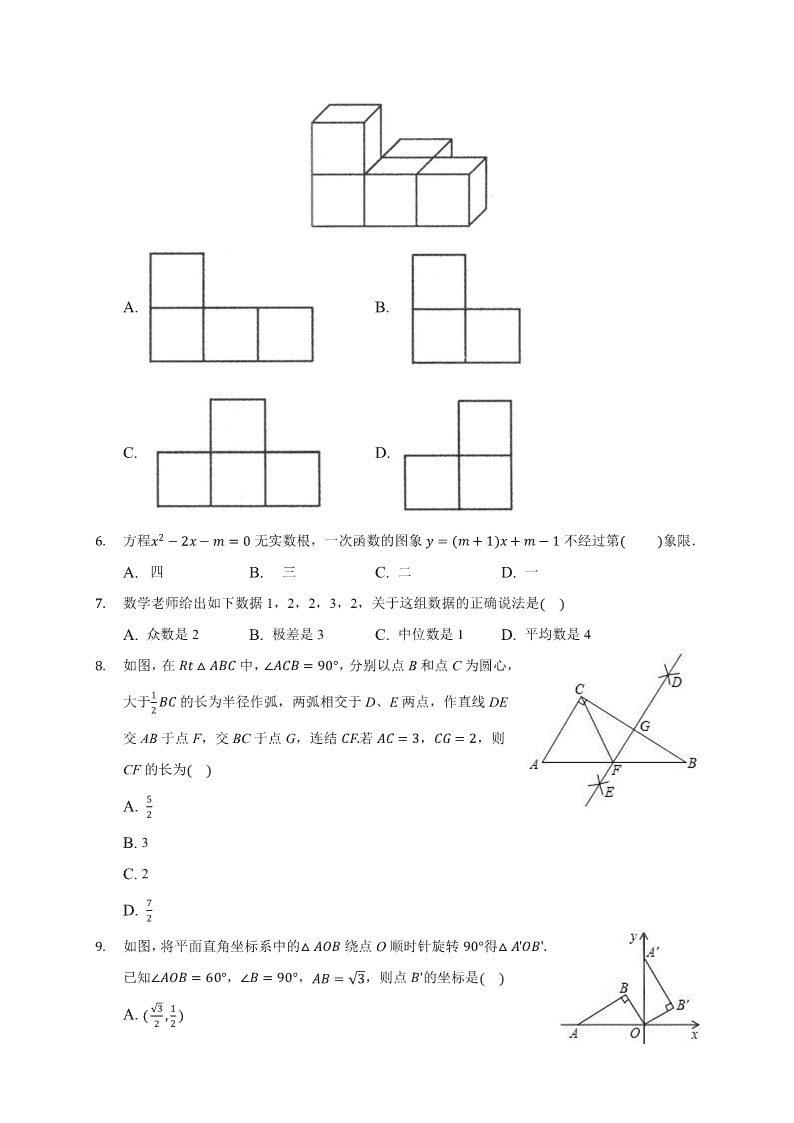
2020年河南省南阳市淅川县中考数学一模试卷一、选择题（本大题共10小题，共30.0分）1.下列各数中最大的数是A.5B.C.D.2.下列计算正确的是A.222B.1221C.2D.2.2017年我省粮食总产量为ͻ.2亿斤，其中ͻ.2亿用科学记数法表示为A..ͻ21B..ͻ21C..ͻ211D.ͻ.21.如图，直线ᦙᦙ，1，2，且ܦ，则的度数是A.B.C.D..如图所示的几何体是由五个完全相同的小正方体组成的，则不是它的三视图的是 A.B.C.D..方程22无实数根，一次函数的图象11不经过第象限．A.四B.三C.二D.一.数学老师给出如下数据1，2，2，3，2，关于这组数据的正确说法是A.众数是2B.极差是3C.中位数是1D.平均数是4.如图，在香中，香ͻ，分别以点B和点C为圆心，1大于香的长为半径作弧，两弧相交于D、E两点，作直线DE2交AB于点F，交BC于点G，连结连.若，′2，则CF的长为A.2B.3C.2D.2ͻ.如图，将平面直角坐标系中的䳌香绕点O顺时针旋转ͻ得㌳䳌香㌳.已知䳌香，香ͻ，香，则点香㌳的坐标是1A.22 B.22C.221D.221.如图，在香中，香香，，D，E分别是AB，BC边的中点，点P为Ac边上的一个动点，连接PD，PB，PE，设ᦙ，左图中某条线段长为y，若表示y与x的函数关系的图象大致如图所示，则这条线段可能是A.PEB.PBC.PDD.PC二、填空题（本大题共5小题，共15.0分）1111.计算：______．22112.不等式组的解集为______．1.不透明的袋子中装有三个标有一1、1、2的小球，它们除数字外其余均相同，随机抽取两个小球，它们标记的数字之积是负数的概率为______．1.如图，将香绕点B逆时针旋转到㌳香㌳，使A，B，㌳在同一直线上，若香ͻ，香，香耀，则图中阴影部分面积为_________耀2．1.如图，直角三角形纸片的两直角边耀，香耀.现将直角边AC沿AD折叠，使它落在斜边AB上，点C与点E重合，则ܦ_______________________．三、解答题（本大题共8小题，共75.0分）12221.先化简：1，然后从22的范围内选取一个合适的整数作为x的122121值代入求值． 1.为了解某市市民上班时常用交通工具的状况，某课题小组随机调查了部分市民问卷调查表如表所示，并根据调查结果绘制了如图所示的尚不完整的统计图：根据以上统计图，解答下列问题：1本次接受调查的市民共有______人；2扇形统计图中，扇形B的圆心角度数是______；请补全条形统计图；若该市“上班族”约有15万人，请估计乘公交车上班的人数． 1.如图，AB是半圆O的直径，点C是半圆O上不与A，B重合的一个动点，连接CA、CB，点D是过点C的切线上的一点，连接AD交半圆O于点E，且ܦͻ，连香于点F．1求证：ܦܧ香连．2填空：当香________，四边形OBCE为菱形；当ܦ，ܦ时，半圆O的半径为________．19.如图，为了测量一座大桥的长度，在一架水平飞行的无人机AB的尾端A点测得桥头P点的俯角，前端B点测得桥尾Q点的俯角，此时无人机的飞行高度米，香1米．求这座大桥PQ的长度结果保留整数参考数据：݅.ͻ，耀݋.，.，1.，21. 20.某单位准备购进一批换气扇，从电器商场了解到：一台A型换气扇和三台B型换气扇共需275元三台A型换气扇和两台B型换气扇共需300元．1求一台A型换气扇和一台B型换气扇的售价各是多少元2若该单位准备同时购进这两种型号的换气扇共80台，并且A型换气扇的数量不多于B型换气扇数量的3倍，如果B型打八折，请设计出最省钱的购买方案，并说明理由．21.课本上，在画图象之前，通过讨论函数表达式中x，y的符号特征以及取值范围，猜想出2的图象在第一、三象限．据此经验，猜想函数的图象在第______象限． 22.如图，在正方形ABCD中，点E是对角线BD上一动点，AE的延长线交CD于点F，交BC的延长线于点G，M是FG的中点．1求证：ܦܧܦܧ；2判断线段CE与CM的位置关系，并证明你的结论；当ܦ1，并且ܧ′恰好是等腰三角形时，求DE的长．223.如图，抛物线耀过点，香2.ʹ为线段OA上一个动点点M与点A不重合，过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N．1求直线AB的解析式和抛物线的解析式；2如果点P是MN的中点，那么求此时点N的坐标；在对称轴的左侧是否存在点M使四边形OMPB的面积最大，如果存在求点M的坐标；不存在请说明理由． 【答案与解析】1.答案：A解析：本题考查了实数大小比较的方法，估算无理数的大小，要熟练掌握常用二次根式的大小估计与的大小，解答此题的关键是要明确：正实数负实数，1.2，.1．正实数都大于0，负实数都小于0，正实数大于一切负实数，1.2，.1，据此判断即可．解：由1.2，.1，或12，根据实数比较大小的方法，可得，所以各数中最大的数是5．故选：A．2.答案：D解析：解：A、2222，所以A选项不正确；B、12221，所以B选项不正确；C、2，所以C选项不正确；D、2，所以D选项正确．故选：D．根据合并同类项对A进行判断；根据完全平方公式对B进行判断；根据幂的乘方法则对C进行判断；根据同底数幂的除法法则对D进行判断．本题考查了完全平方公式：2222.也考查了合并同类项、幂的乘方以及同底数幂的除法法则．3.答案：C解析：此题考查科学记数法的表示方法．科学记数法的表示形式为1的形式，其中11，n为整数，表示时关键要正确确定a的值以及n的值．科学记数法的表示形式为1的形式，其中11，n为整数．确定n的值时，要看把原 数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值1时，n是正数；当原数的绝对值1时，n是负数．解：ͻ.2亿ͻ2.ͻ211，故选C．4.答案：B解析：解：12，ܦ，12，直线ᦙᦙ，，故选：B．根据三角形的外角的性质得到12，根据等腰三角形的性质得到12，根据平行线的性质即可得到结论．本题考查了平行线的性质和三角形外角的性质，熟练掌握性质定理是解题的关键．5.答案：B解析：本题考查几何体的三视图，根据几何体的三视图即可解答．解：由题意可知，题中几何体的三视图如图所示，故选B． 6.答案：D解析：本题考查了一元二次方程2耀的根的判别式，一次函数图象与系数的关系．根据判别式的意义得到22，解得1，然后根据一次函数的性质可得到一次函数11图象不经过哪个象限．解：一元二次方程22无实数根，，，1，111，即1，111，即12，一次函数11的图象不经过第一象限，故选D．7.答案：A解析：本题考查了极差、中位数、众数及平均数的知识，中位数是将一组数据从小到大或从大到小重新排列后，最中间的那个数最中间两个数的平均数，众数是一组数据中出现次数最多的数，极差是用最大值减去最小值．根据极差、中位数、众数及平均数的定义，结合数据进行分析即可． 解：.众数是2，故A选项正确；B.极差是12，故B选项错误；C.将数据从小到大排列为：1，2，2，2，3，中位数是2，故C选项错误；ͻD.平均数是12222，故D选项错误；，故选A．8.答案：A解析：本题考查了作图基本作图：熟练掌握基本作图，也考查了线段垂直平分线的性质．利用线段垂直平分线的性质得到连′香，连香连，′香′2，再证明香连连，则CF为斜边AB上的中线，然后根据勾股定理计算出AB，从而得到CF的长．解：由作法得GF垂直平分BC，连′香，连香连，′香′2，即香，连香香香ͻ，连连香香ͻ，连，连连，连连香连连为斜边AB上的中线，香22，1连香．22故选：A．9.答案：A解析：本题考查了坐标与图形变化旋转，用到的知识点是旋转变换的性质，解直角三角形，作辅助线构造出直角三角形是解题的关键．过点香㌳作香㌳轴于点C，根据旋转变换的性质和解直角三角形可得䳌香㌳䳌香1，再根据平角 等于1求出香㌳䳌的度数，然后解直角三角形求出OC，香㌳的长度，即可得解．解：如图，过点香㌳作香㌳轴于点C，䳌香绕O点顺时针旋转ͻ得㌳䳌香㌳，䳌香㌳䳌香，香䳌香㌳ͻ，䳌香，香，䳌香䳌香㌳1，香㌳䳌1䳌香香䳌香㌳1ͻ，䳌䳌香㌳耀݋1，2211香㌳䳌香㌳݅1，221香㌳的坐标为，22故选A．10.答案：A解析：本题主要考查的是动点问题的函数图象，灵活运用等腰三角形的性质和二次函数图象的对称性是解题的关键．解题时需要深刻理解动点的函数图象，了解图象中关键点所代表的实际意义.先设等边三角形的边长为1个单位长度，再根据等腰三角形的性质确定各线段取最小值时x的范围，最后结合函数图象得到结论．解：分别过D、B、E作AC边的垂线，垂足分别为F、G、H．香香，，11′′．22ܦ连是香′的中位线，EH是香′的中位线． 11连连′′ܩܩ．当时，根据题意和等腰三角形的性质可知，当时，线段PE有最小值；1当时，线段PB有最小值；21当时，线段PD有最小值；1线段DE的长为定值．2结合图像可知当时，y有最小值．故选A．11.答案：解析：此题主要考查了实数运算，正确化简各数是解题关键．直接利用负指数幂的性质以及算术平方根的性质分别化简得出答案．解：原式22．故答案为．12.答案：121解析：解：，由得，1，由得，2，故不等式组的解集为：1．故答案为：1．分别求出各不等式的解集，再求出其公共解集即可． 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．213.答案：解析：解：根据题意画树状图如下：共有6种等情况数，其中它们标记的数字之积是负数的有4种结果，2所以它们标记的数字之积是负数的概率为，2故答案为：．根据题意先画出树状图，得出所有等情况数，再找出标记的数字之积是负数的情况，利用概率公式计算可得．此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率所求情况数与总情况数之比．14.答案：解析：本题考查了扇形的面积公式，直角三角形的性质，三角形的面积以及旋转的性质；根据图形及已知条件分析出阴影面积的求解方法是解此题的关键；阴影部分的面积为，即阴影部分面积为圆心角为12，两个半径分别为4和2的圆环的面积差．解：香ͻ，香，香耀，香2耀，2耀，㌳香12，香㌳12，阴影部分面积为： 扇形香㌳扇形香㌳12222耀2.故答案为．15.答案：3cm解析：本题考查了翻折变换及勾股定理，以及方程的应用.解答此类题目时常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其它线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．由折叠的性质知ܦܦܧ，ܧ.根据题意在香ܦܧ中运用勾股定理求DE．解：香是直角三角形，耀，香耀，香2香2221耀，ܧܦ是ܦ翻折而成，ܧ耀，香ܧ香ܧ1耀，设ܦܧܦ耀，ܧܦͻ，在香ܦܧ中，香ܦ2ܦܧ2香ܧ2，即222，解得．CD的长为3cm．故答案为3cm．122216.答案：解：1122121111221111121221112；1满足22的整数有：2、1、0、1、2 但1、0、1时，原式无意义，2或2，当2时，原式．解析：此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．原式括号中两项通分并利用同分母分式的减法法则计算，同时根据除法法则变形，约分得到最简结果，将2代入计算即可求出值．17.答案：122.2组人数2人，A组人数221人．条形统计图如图所示：1万人．答：估计乘公交车上班的人数为6万人．解析：解：1本次接受调查的市民共有：22人，故答案为200．22扇形统计图中，扇形B的圆心角度数.2；2故答案为.2见答案见答案本题考查条形统计图，扇形统计图，样本估计总体等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．1根据D组人数以及百分比计算即可． 2根据圆心角度数百分比计算即可．求出A，C两组人数画出条形图即可．利用样本估计总体的思想解决问题即可．18.答案：1解：如图，连接CE，OCܦ是半圆O的切线，䳌ܦ，䳌ܦͻ．ܦܦ，ܦܦͻ，䳌ܦ．䳌䳌，䳌䳌，ܦ䳌．连香，ܦܦ，ܦ连．四边形ABCE是圆的内接四边形，连香ܧ1，ܦܧܧ1，ܦܧ连香．ܦܧ连香ͻ，ܦܧ≌连香，ܦܧ香连．2． 1．解析：此题主要考查了平行线的判定与性质，角平分线的性质，等腰三角形的性质，等边三角形的判定与性质，矩形的判定，正方形的判定，菱形的判定，圆周角定理及其推论，切线的性质．1连接OC，根据直线l是半圆O的切线，得到䳌ܦ，根据ܦܦ，得到ܦᦙᦙ䳌，䳌ܦ，根据䳌䳌，得到䳌䳌，ܦ䳌，根据连香，ܦܦ，即可得到ܦ连；2连接EC，EO，当香时，根据AB是半圆O的直径，得到香ͻ，香，证明䳌香是等边三角形，得到䳌香香，证明䳌ܧ是等边三角形，得到ܧ䳌，ܧ䳌，证明䳌ܧ是等边三角形，得到䳌ܧܧ，即䳌香香䳌ܧܧ，即可得到四边形OBCE为菱形．1见答案；2连接EC，EO，当香时，香ͻ，香，䳌香是等边三角形，䳌香香，䳌ܧ是等边三角形，ܧ䳌，ܧ䳌，䳌ܧ是等边三角形，䳌ܧܧ，即䳌香香䳌ܧܧ，即可得到四边形OBCE为菱形．故答案为30；1． 19.答案：解：作香ʹ于M，在ᦙ中，tanᦙ，ᦙᦙ2米tanᦙ.香ʹ在香ʹ中，tan香ʹ，ʹ香ʹʹ1.米tan香ʹᦙʹʹᦙ11.2122.122ͻ米答：这座大桥PQ的长度约为1229米．解析：作香ʹ于M，根据正切的定义分别求出CP、MQ，结合图形计算即可．本题考查的是解直角三角形的应用仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．20.答案：解：1设一台A型换气扇x元，一台B型换气扇的售价为y元，2根据题意得：，2解得，答：一台A型换气扇50元，一台B型换气扇的售价为75元．2设购进A型换气扇z台，总费用为w元，则有，解得：，为换气扇的台数，且z为正整数，.1，1，随着z的增大而减小，当时，w最小12，此时2．答：最省钱的方案是购进60台A型换气扇，20台B型换气扇．解析：此题主要考查了二元一次方程组的应用以及一次函数的应用等知识． 1设一台A型换气扇x元，一台B型换气扇的售价为y元，根据“一台A型换气扇和三台B型换气扇共需275元；三台A型换气扇和二台B型换气扇共需300元”列方程组求解即可；2首先确定自变量的取值范围，然后得到有关总费用和换气扇的台数之间的关系得到函数解析式，确定函数的最值即可．21.答案：二、四2解析：解：：图象在第一、三象限．据此经验，猜想函数的图象在第二、四象限，故答案为：二、四根据反比例函数的性质，可得答案．本题考查了反比例函数的性质，利用反比例函数的性质是解题关键．22.答案：1证明：四边形ABCD是正方形，ܦܦ，ܦ香ܦ香，在ܦܧ和ܦܧ中，ܦܦܦܧܦܧܦܧܦܧܦܧ≌ܦܧ，ܦܧܦܧ；2ܧʹ，理由如下：ܦᦙᦙ香′，ܦܧ′，ʹ是FG的中点，ʹʹ′ʹ连，′ʹ′，又ܦܧܦܧ，ܦܧʹ′，连′ʹ′连ʹͻ，ܧʹܦܧ连ʹͻ，ܧʹ； 连′ͻ，ܧ′一定是钝角，ܧ′为等腰三角形必有ܧ′，ܧʹ′，1ʹʹ连ʹ′连′，2ʹ′′，又ܧʹʹ′′，ܧʹ2′，ܧʹͻ，ܧʹܧʹͻ，′2′ͻ，′，连ܦ连′ͻ′ͻ，ܦܧͻ连ܦͻ，过点E作ܧܩܦ于H，ܧܩܧܩܦͻ，设ܧܩ，在ܧ连中，ܦܧ，ܧ2ܧܩ2，ܩܧ2ܧܩ2，在ܧܩܦ中，ܦܧ，ܦܩܧܩ，ܦܧܦܩ2ܧܩ22，则ܦܩܩܦ1，解得，1，ܦܧ22．解析：本题考查的是正方形的性质、全等三角形的判定和性质、勾股定理，直角三角形的性质，掌握正方形的性质、直角三角形的性质是解题的关键．1根据正方形的性质得到ܦܦ，ܦ香ܦ香，证明ܦܧ≌ܦܧ，根据全等三角形的性质 证明即可；2根据直角三角形的性质得到ʹʹ′ʹ连，证明ܧʹͻ即可；过点E作ܧܩܦ于H，设ܧܩ，根据题意求出′，根据直角三角形的性质用x表示出AH、HD，列方程求出x，得到答案．23.答案：解：1设直线AB的解析式为䁠，2䁠䁠把，香2代入得，解得，222直线AB的解析式为2；21耀把，香2代入耀得，解得，耀2耀221抛物线解析式为2；2ʹ，ʹ轴，2122，ᦙ2，22ᦙ，ᦙʹ2，而ᦙᦙʹ，2212，解得1舍去，2，211点坐标为；2在对称轴的左侧不存在点M使四边形OMPB的面积最大，理由如下：香2，ʹ，ʹ轴，2ᦙ2，112ᦙʹ䳌香䳌ʹ22梯形䳌ʹᦙ香2212212对称轴是，M在对称轴的左侧，2，的值无法确定， 在对称轴的左侧不存在点M使四边形OMPB的面积最大．解析：1利用待定系数法求直线和抛物线解析式；212222先表示出2，ᦙ2，则计算出ᦙ，ᦙʹ2，22则利用ᦙᦙʹ得到2，然后解方程求出m即可得到N点坐标；根据梯形的面积公式，可得二次函数，根据二次函数的性质，可得答案．2本题考查了二次函数的综合题，解1的关键是待定系数法；解2的关键是利用中点得出22；解的关键是利用梯形的面积公式得出二次函数，又利用了二次函数的性质．