人教版九年级数学下册-第28章检测题 5页

第28章检测题(时间：100分钟满分：120分)一、选择题(每小题3分，共30分)1．(2020·玉林)sin45°的值是(B)A．B．C．D．12．在Rt△ABC中，∠C＝90°，sinA＝，则tanB的值为(A)A．B．C．D．3．在等腰△ABC中，AB＝AC＝5，BC＝6，那么sinB的值是(C)A．B．C．D．4．(2020·杭州)如图，在△ABC中，∠C＝90°，设∠A，∠B，∠C所对的边分别为a，b，c，则(B)A．c＝bsinBB．b＝csinBC．a＝btanBD．b＝ctanB5．如图，在Rt△ABC中，CD是斜边AB上的高，已知∠ACD的正弦值是，则的值是(D)A．B．C．D．6．(2020·荆州)如图，在平面直角坐标系中，Rt△OAB的斜边OA在第一象限，并与x轴的正半轴夹角为30°.C为OA的中点，BC＝1，则点A的坐标为(B)A．(，)B．(，1)C．(2，1)D．(2，)7．(2020·温州)如图，在离铁塔150米的A处，用测倾仪测得塔顶的仰角为α，测倾仪高AD为1.5米，则铁塔的高BC为(A)A．(1.5＋150tanα)米B．(1.5＋)米C．(1.5＋150sinα)米D．(1.5＋)米8．(2020·益阳)如图，在矩形ABCD中，E是DC上的一点，△ABE是等边三角形，AC交BE于点F，则下列结论不成立的是(B)A．∠DAE＝30°B．∠BAC＝45°C．＝D．＝9．(2020·重庆)如图，垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处，某测量员从山脚C点出发沿水平方向前行78米到D点(点A，B，C在同一直线上)，再沿斜坡DE方向前行78米到E点(点A，B，C，D，E在同一平面内)，在点E处测得5G信号塔顶端A的仰角为43°，悬崖BC的高为144.5米，斜坡DE的坡度(或坡比)i＝1∶2.4，则信号塔AB的高度约为(参考数据：sin43°≈0.68，cos43°≈0.73，tan43°≈0.93)(D)A．23米B．24米C．24.5米D．25米10．(长沙中考)如图，△ABC中，AB＝AC＝10，tanA＝2，BE⊥AC于点E，D是线段BE 上的一个动点，则CD＋BD的最小值是(B)A．2B．4C．5D．10二、填空题(每小题3分，共15分)11．(甘肃中考)在△ABC中，∠C＝90°，tanA＝，则cosB＝．12．(2020·南通)如图，测角仪CD竖直放在距建筑物AB底部5m的位置，在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m，则建筑物AB的高度约为__7.5__m．(结果保留小数点后一位，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19)13．(2020·咸宁)如图，海上有一灯塔P，位于小岛A北偏东60°方向上，一艘轮船从小岛A出发，由西向东航行24nmile到达B处，这时测得灯塔P在北偏东30°方向上，如果轮船不改变航向继续向东航行，当轮船到达灯塔P的正南方，此时轮船与灯塔P的距离是__20.8__nmile.(结果保留一位小数，≈1.73)14．(2020·荆州)“健康荆州，你我同行”，市民小张积极响应“全民健身动起来”号召，坚持在某环形步道上跑步．已知此步道外形近似于如图所示的Rt△ABC，其中∠C＝90°，AB与BC间另有步道DE相连，D地在AB正中位置，E地与C地相距1km.若tan∠ABC＝，∠DEB＝45°，小张某天沿A→C→E→B→D→A路线跑一圈，则他跑了__24__km.15．(2020·深圳)如图，在四边形ABCD中，AC与BD相交于点O，∠ABC＝∠DAC＝90°，tan∠ACB＝，＝，则＝____．三、解答题(共75分)16．(8分)计算：(1)3tan30°＋cos245°－2sin60°；(2)tan260°－2sin45°＋cos60°.解：原式＝解：原式＝－17．(9分)在△ABC中，∠C＝90°.(1)已知c＝8，∠A＝60°，求∠B，a，b；(2)已知a＝3，∠A＝30°，求∠B，b，c.解：(1)∠B＝30°，a＝12，b＝4(2)∠B＝60°，b＝9，c＝618．(9分)(2020·盐城)如图，在△ABC中，∠C＝90°，tanA＝，∠ABC的平分线BD交AC于点D，CD＝，求AB的长． 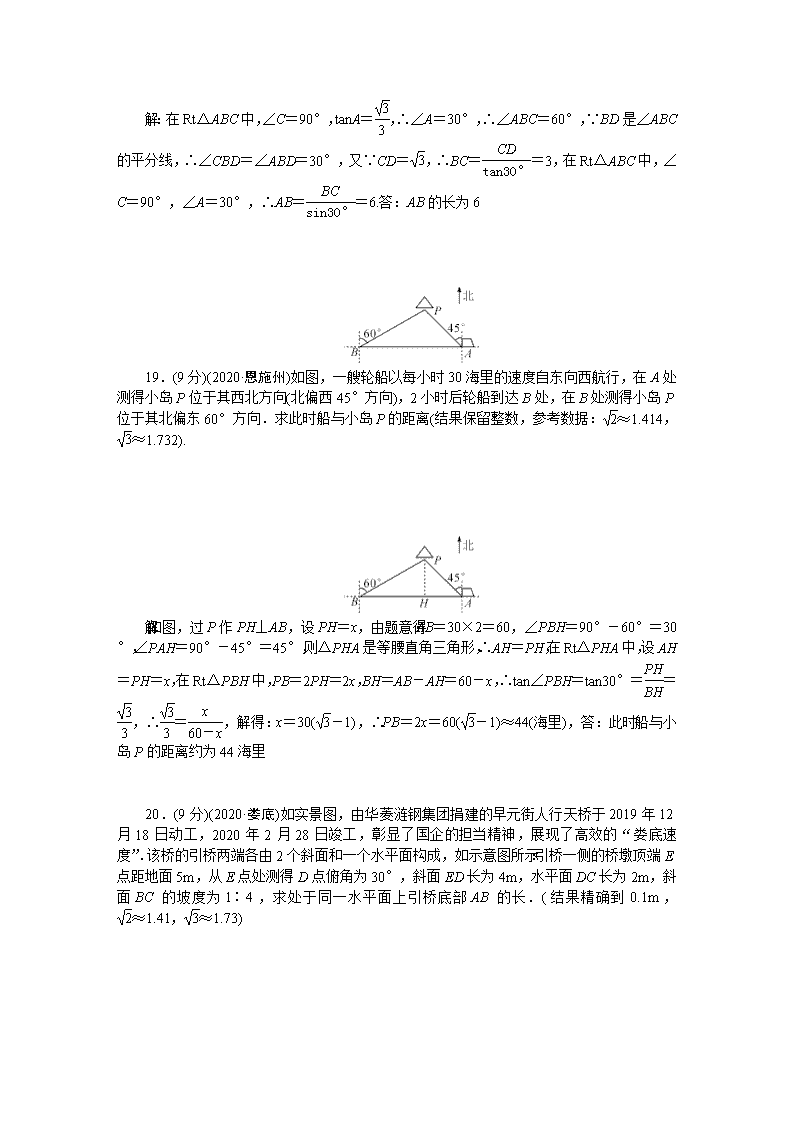解：在Rt△ABC中，∠C＝90°，tanA＝，∴∠A＝30°，∴∠ABC＝60°，∵BD是∠ABC的平分线，∴∠CBD＝∠ABD＝30°，又∵CD＝，∴BC＝＝3，在Rt△ABC中，∠C＝90°，∠A＝30°，∴AB＝＝6.答：AB的长为619．(9分)(2020·恩施州)如图，一艘轮船以每小时30海里的速度自东向西航行，在A处测得小岛P位于其西北方向(北偏西45°方向)，2小时后轮船到达B处，在B处测得小岛P位于其北偏东60°方向．求此时船与小岛P的距离(结果保留整数，参考数据：≈1.414，≈1.732).解：如图，过P作PH⊥AB，设PH＝x，由题意得：AB＝30×2＝60，∠PBH＝90°－60°＝30°，∠PAH＝90°－45°＝45°，则△PHA是等腰直角三角形，∴AH＝PH，在Rt△PHA中，设AH＝PH＝x，在Rt△PBH中，PB＝2PH＝2x，BH＝AB－AH＝60－x，∴tan∠PBH＝tan30°＝＝，∴＝，解得：x＝30(－1)，∴PB＝2x＝60(－1)≈44(海里)，答：此时船与小岛P的距离约为44海里20．(9分)(2020·娄底)如实景图，由华菱涟钢集团捐建的早元街人行天桥于2019年12月18日动工，2020年2月28日竣工，彰显了国企的担当精神，展现了高效的“娄底速度”．该桥的引桥两端各由2个斜面和一个水平面构成，如示意图所示：引桥一侧的桥墩顶端E点距地面5m，从E点处测得D点俯角为30°，斜面ED长为4m，水平面DC长为2m，斜面BC的坡度为1∶4，求处于同一水平面上引桥底部AB的长．(结果精确到0.1m，≈1.41，≈1.73) 解：作DF⊥AE于F，DG⊥AB于G，CH⊥AB于H，如图所示：则DF＝GA，DC＝GH＝2，AF＝DG＝CH，由题意得：∠EDF＝30°，∴EF＝DE＝×4＝2，DF＝EF＝2，∵AE＝5，∴CH＝AF＝AE－EF＝5－2＝3，∵斜面BC的坡度为1∶4＝，∴BH＝4CH＝12，∴AB＝AG＋GH＋BH＝2＋2＋12＝2＋14≈17.5(m)，答：处于同一水平面上引桥底部AB的长约为17.5m21．(10分)如图，AB是⊙O的直径，AB＝10，DC与⊙O相切于点C，AD⊥DC，垂足为D，AD交⊙O于点E.(1)求证：AC平分∠BAD；(2)若sin∠BEC＝，求DC的长．解：(1)连接OC，∵DC是切线，∴OC⊥DC，又∵AD⊥DC，∴AD∥OC，∴∠DAC＝∠ACO，又OA＝OC，∴∠BAC＝∠ACO，∴∠DAC＝∠BAC，∴AC平分∠BAD　(2)∵AB为直径，∴∠ACB＝90°，又∠BAC＝∠BEC，∴BC＝AB·sin∠BAC＝6，∴AC＝8，∴CD＝AC·sin∠DAC＝22．(10分)(2020·鄂州)鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度CD.如图所示，一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为α，无人机沿水平线AF方向继续飞行50米至B处，测得正前方河流右岸D处的俯角为30°.线段AM的长为无人机距地面的铅直高度，点M，C，D在同一条直线上．其中tanα＝2，MC＝50米．(1)求无人机的飞行高度AM；(结果保留根号)(2)求河流的宽度CD.(结果精确到1米，参考数据：≈1.41，≈1.73) 解：过点B作BN⊥MD，垂足为N，由题意可知，∠ACM＝α，∠BDM＝30°，AB＝MN＝50，(1)在Rt△ACM中，tanα＝2，MC＝50，∴AM＝2MC＝100＝BN，答：无人机的飞行高度AM为100米　(2)在Rt△BND中，∵tan∠BDN＝，即：tan30°＝∴DN＝300，∴DM＝DN＋MN＝300＋50＝350，∴CD＝DM－MC＝350－50≈264，答：河流的宽度CD约为264米23．(11分)(2020·黄冈)因东坡文化远近闻名的遗爱湖公园，“国庆黄金周”期间，游人络绎不绝，现有一艘游船载着游客在遗爱湖中游览，当船在A处时，船上游客发现岸上P1处的临摹亭和P2处的遗爱亭都在东北方向，当游船向正东方向行驶600m到达B处时，游客发现遗爱亭在北偏西15°方向，当游船继续向正东方向行驶400m到达C处时，游客发现临摹亭在北偏西60°方向．(1)求A处到临摹亭P1处的距离；(2)求临摹亭P1处与遗爱亭P2处之间的距离．(计算结果保留根号)解：(1)如图，作P1M⊥AC于M，设P1M＝x，在Rt△P1AM中，∵∠P1AB＝45°，∴AM＝P1M＝x，在Rt△P1CM中，∵∠P1CA＝30°，∴MC＝P1M＝x，∵AC＝1000，∴x＋x＝1000，解得x＝500(－1)，∴P1M＝500(－1)m，∴P1A＝＝500(－)m，故A处到临摹亭P1处的距离为500(－)m　(2)如图，作BN⊥AP2于N，∵∠P2AB＝45°，∠P2BA＝75°，∴∠P2＝60°，在Rt△ABN中，∵∠P1AB＝45°，AB＝600m，∴BN＝AN＝AB＝300，∴P1N＝P1A－AN＝500(－)－300＝500－800，在Rt△P2BN中，∵∠P2＝60°，∴P2N＝BN＝×300＝100，∴P1P2＝P2N－P1N＝100－(500－800)＝800－400.故临摹亭P1处与遗爱亭P2处之间的距离是(800－400)m