2020届苏科版九年级上册期末调研考试数学试题（苏教版九年级数学上册期末考试测试卷） 3页

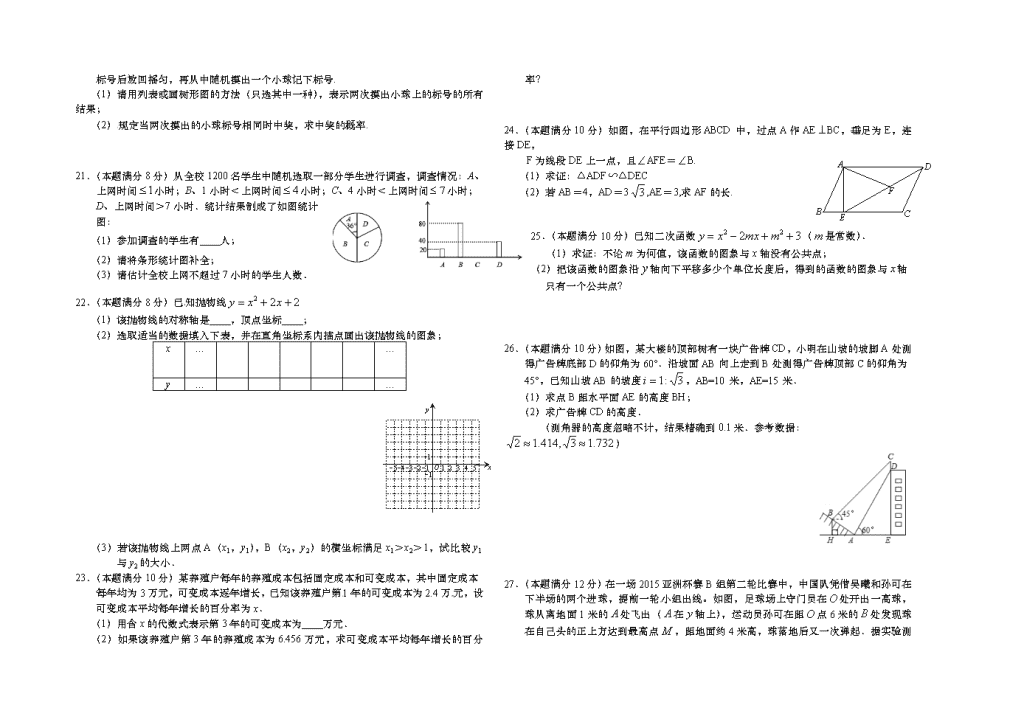
苏教版九年级数学上册期末学情调研试题一、选择题（本大题共有８小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）1．的值是A．B．0C．1D．2．一元二次方程的解是A．x1=1，x2=2B．C．D．x1=0，x2=23．县医院住院部在连续10天测量某病人的体温与36℃的上下波动数据为：0.2,0.3,0.1,0.1,0,0.2,0.1,0.1,0.1,0,则对这10天中该病人的体温波动数据分析不正确的是A．平均数为0.12B．众数为0.1C．中位数为0.1D．方差为0.024．△ABC为⊙O的内接三角形，若∠AOC＝160°，则∠ABC的度数是A．80°B．160°C．100°D．80°或100°5．若二次函数的与的部分对应值如下表：-7-6-5-4-3-2y-27-13-3353则当时，的值为A．5B．-3C．-13D．-276．如图，在平面直角坐标系中，⊙A经过原点O，并且分别与x轴、y轴交于B、C两点，已知B（8，0），C（0，6），则⊙A的半径为A．3B．4C．5D．87．如图，在△ABC中，EF∥BC，，S四边形BCFE=8，则S△ABC等于AEFBCA．9B．10C．12D．138．二次函数的图象如图所示，反比例函数与正比例函数在同一坐标系中的大致图象可能是xxxxxyyyyyABCD二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请将答案直接写在答题卡相应位置上）9．如果线段c是a、b的比例中项，且a=4，b=9，则c=．CDAB（13题）10．不透明的袋子中装有4个红球、3个黄球和5个蓝球，每个球除颜色不同外其它都相同，从中任意摸出一个球，则摸出球的可能性最大．11．两个相似三角形的面积比为4：9，那么它们对应中线的比为．12．若等腰三角形的两边分别为8和10，则底角的余弦值为．13．在等腰直角△ABC中，∠C＝90°，AC＝6，D为AC上一点，若，则AD＝______。14．已知一组数据x1，x2，x3，x4，x5的方差是，那么另一组数据3x1-2，3x2-2，3x3-2，3x4-2，3x5-2的方差是．15．若抛物线y＝x2－kx＋k－1的顶点在轴上，则k＝．16．已知圆锥的底面半径为3，侧面积为15，则这个圆锥的高为．17．把一个矩形剪去一个正方形，若剩下的矩形与原矩形相似，则原矩形的长边与短边之比为18．如图，在相距2米的两棵树间拴一根绳子做一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小芳距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为米.三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）19．（本题满分8分）（1）计算：（2）解方程：20．（本题满分8分）九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球，把它们分别标号1、2、3. 随机摸出一个小球记下标号后放回摇匀，再从中随机摸出一个小球记下标号.（1）请用列表或画树形图的方法（只选其中一种），表示两次摸出小球上的标号的所有结果；（2）规定当两次摸出的小球标号相同时中奖，求中奖的概率.21．（本题满分8分）从全校1200名学生中随机选取一部分学生进行调查，调查情况：A、上网时间小时；B、1小时＜上网时间小时；C、4小时＜上网时间小时；D、上网时间＞7小时．统计结果制成了如图统计图：（1）参加调查的学生有　　人；（2）请将条形统计图补全；（3）请估计全校上网不超过7小时的学生人数．22．（本题满分8分）已知抛物线（1）该抛物线的对称轴是　　，顶点坐标　　；（2）选取适当的数据填入下表，并在直角坐标系内描点画出该抛物线的图象；x……y……（3）若该抛物线上两点A（x1，y1），B（x2，y2）的横坐标满足x1＞x2＞1，试比较y1与y2的大小．23．（本题满分10分）某养殖户每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为3万元，可变成本逐年增长，已知该养殖户第1年的可变成本为2.4万元，设可变成本平均每年增长的百分率为x．（1）用含x的代数式表示第3年的可变成本为　　万元．（2）如果该养殖户第3年的养殖成本为6.456万元，求可变成本平均每年增长的百分率？24．（本题满分10分）如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，CDABEFF为线段DE上一点，且∠AFE＝∠B.（1）求证：△ADF∽△DEC（2）若AB＝4，AD＝3,AE＝3,求AF的长.25．（本题满分10分）已知二次函数（是常数）．（1）求证：不论为何值，该函数的图象与x轴没有公共点；（2）把该函数的图象沿轴向下平移多少个单位长度后，得到的函数的图象与轴只有一个公共点？26．（本题满分10分）如图，某大楼的顶部树有一块广告牌CD，小明在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度，AB=10米，AE=15米．（1）求点B距水平面AE的高度BH；（2）求广告牌CD的高度．（测角器的高度忽略不计，结果精确到0.1米．参考数据：）27．（本题满分12分）在一场2015亚洲杯赛B组第二轮比赛中，中国队凭借吴曦和孙可在下半场的两个进球，提前一轮小组出线。如图，足球场上守门员在处开出一高球，球从离地面1米的处飞出（在轴上），运动员孙可在距点6米的处发现球在自己头的正上方达到最高点，距地面约4 米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．（1）求足球开始飞出到第一次落地时，该抛物线的函数表达式．（2）足球第一次落地点距守门员多少米？（取）（3）孙可要抢到足球第二个落地点，他应从第一次落地点再向前跑多少米？（取）28．（本题满分12分）如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．ABDCO●E求证：（1）D是BC的中点；（2）△BEC∽△ADC；（3）若，求⊙O的半径。