人教版 九年级数学上册 第23章 旋转 课时训练 11页

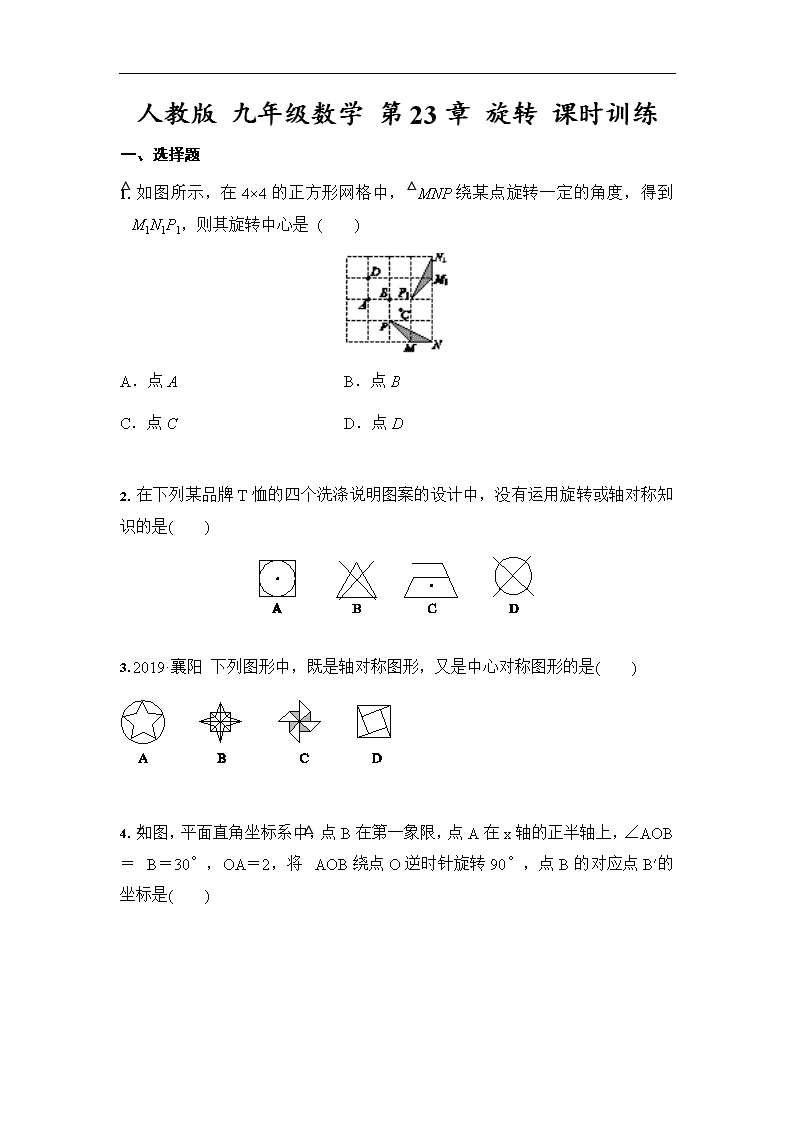
人教版九年级数学第23章旋转课时训练一、选择题1.如图所示，在4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心是(　　)A．点AB．点BC．点CD．点D2.在下列某品牌T恤的四个洗涤说明图案的设计中，没有运用旋转或轴对称知识的是(　　)3.2019·襄阳下列图形中，既是轴对称图形，又是中心对称图形的是(　　)4.如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2，将△AOB绕点O逆时针旋转90°，点B的对应点B′的坐标是(　　) A．(－1，2＋)B．(－，3)C．(－，2＋)D．(－3，)5.如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列结论一定正确的是(　　)A．AC＝ADB．AB⊥EBC．BC＝DED．∠A＝∠EBC 6.如图，Rt△OCB的斜边在y轴上，OC＝，含30°角的顶点与原点重合，直角顶点C在第二象限，将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′，则点B的对应点B′的坐标是(　　)A．(，－1)B．(1，－)C．(2，0)D．(，0)7.在平面直角坐标系中，点A的坐标为(1，)，以原点为中心，将点A 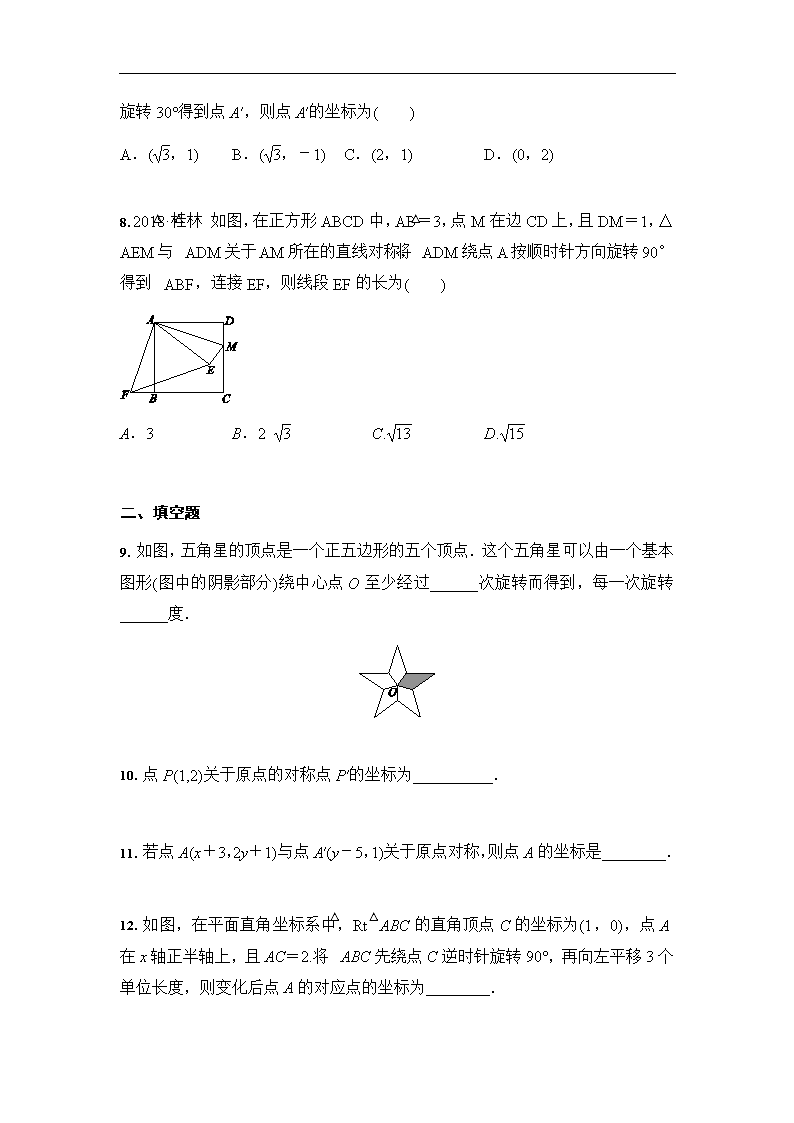顺时针旋转30°得到点A′，则点A′的坐标为(　　)A．(，1)B．(，－1)C．(2，1)D．(0，2)8.2018·桂林如图，在正方形ABCD中，AB＝3，点M在边CD上，且DM＝1，△AEM与△ADM关于AM所在的直线对称，将△ADM绕点A按顺时针方向旋转90°得到△ABF，连接EF，则线段EF的长为(　　)A．3B．2C.D.二、填空题9.如图，五角星的顶点是一个正五边形的五个顶点．这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过______次旋转而得到，每一次旋转______度．10.点P(1,2)关于原点的对称点P′的坐标为__________．11.若点A(x＋3，2y＋1)与点A′(y－5，1)关于原点对称，则点A的坐标是________．12.如图，在平面直角坐标系中，Rt△ABC的直角顶点C的坐标为(1，0)，点A在x轴正半轴上，且AC＝2.将△ABC先绕点C 逆时针旋转90°，再向左平移3个单位长度，则变化后点A的对应点的坐标为________．13.如图，在△ABC中，∠BAC＝90°，AB＝AC＝10cm，D为△ABC内一点，∠BAD＝15°，AD＝6cm，连接BD，将△ABD绕点A逆时针旋转，使AB与AC重合，点D的对应点为点E，连接DE，DE交AC于点F，则CF的长为________cm.14.2019·呼和浩特已知正方形的对称中心在坐标原点，顶点A，B，C，D按逆时针依次排列，若点A的坐标为(2，)，则点B与点D的坐标分别为(　　)A．(－2，)，(2，－)B．(－，2)，(，－2)C．(－，2)，(2，－)D．(－，)，(，－)15.如果将点P绕定点M旋转180°后与点Q重合，那么点P与点Q关于点M对称，定点M叫做对称中心，此时，M是线段PQ的中点．如图3，在平面直角坐标系中，△ABO的顶点A，B，O的坐标分别为(1，0)，(0，1)，(0，0)，点P1，P2，P3，…中的相邻两点都关于△ABO的一个顶点对称，点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与点P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称……且这些对称中心依次循环．已知点P1的坐标是(1，1)，则点P2020的坐标为________． 三、解答题16.如图，在△ABC中，∠ACB＝90°，AC＝BC，D是AB边上一点(点D与点A，B不重合)，连接CD，将线段CD绕点C逆时针旋转90°得到线段CE，连接DE交BC于点F，连接BE.(1)求证：△ACD≌△BCE；(2)当AD＝BF时，求∠BEF的度数． 17.如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A(－2，－2)，B(－4，－1)，C(－4，－4)．(1)作出△ABC关于原点O成中心对称的△A1B1C1.(2)作出点A关于x轴的对称点A′.若把点A′向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界)，求a的取值范围． 18.如图，已知△ABC和点O.(1)在图中画出△A′B′C′，使△A′B′C′与△ABC关于点O对称；(2)点A，B，C，A′，B′，C′能组成哪几个平行四边形？请用符号表示出来.人教版九年级数学第23章旋转课时训练-答案一、选择题1.【答案】B　[解析]旋转中心到对应点的距离相等．2.【答案】C　3.【答案】B4.【答案】B 5.【答案】D　[解析]由旋转的性质可知，AC＝CD，但∠A不一定是60°，所以不能证明AC＝AD，所以选项A错误；因为旋转角度不定，所以选项B不能确定；因为不确定AB和BC的数量关系，所以BC和DE的数量关系不能确定，所以选项C不能确定；由旋转的性质可知∠ACD＝∠BCE，AC＝DC，BC＝EC，所以2∠A＝180°－∠ACD，2∠EBC＝180°－∠BCE，从而可证选项D是正确的．6.【答案】A7.【答案】A　[解析]如图，过点A作AE⊥y轴于点E，过点A′作A′F⊥x轴于点F，∴∠AEO＝∠A′FO＝90°.∵点A的坐标为(1，)，∴AE＝1，OE＝，∴OA＝2，∠AOE＝30°，由旋转可知∠AOA′＝30°，OA′＝OA＝2，∴∠A′OF＝90°－30°－30°＝30°，∴A′F＝OA′＝1，OF＝，∴A′(，1)．故选A.8.【答案】C　[解析]如图，连接BM.∵△AEM与△ADM关于AM所在的直线对称， ∴AE＝AD，∠MAD＝∠MAE.∵△ADM绕点A按顺时针方向旋转90°得到△ABF，∴AF＝AM，∠FAB＝∠MAD，∴∠FAB＝∠MAE，∴∠FAB＋∠BAE＝∠BAE＋∠MAE，即∠FAE＝∠MAB，∴△FAE≌△MAB(SAS)，∴EF＝BM.∵四边形ABCD是正方形，∴BC＝CD＝AB＝3.∵DM＝1，∴CM＝2.∵在Rt△BCM中，BM＝＝，∴EF＝.二、填空题9.【答案】4　72　10.【答案】(－1，－2)　11.【答案】(6，－1)　[解析]依题意，得解得∴点A的坐标为(6，－1)． 12.【答案】(－2，2)　[解析]△ABC绕点C逆时针旋转90°后，点A的对应点的坐标为(1，2)，再向左平移3个单位长度，点A的对应点的坐标为(－2，2)．13.【答案】(10－2)　[解析]如图，过点A作AG⊥DE于点G.由旋转知，AD＝AE，∠DAE＝90°，∠CAE＝∠BAD＝15°，∴∠AED＝∠ADG＝45°，∴∠AFD＝∠AED＋∠CAE＝60°.在Rt△ADG中，AG＝DG＝＝3(cm)．在Rt△AFG中，GF＝＝(cm)，AF＝2FG＝2(cm)，∴CF＝AC－AF＝(10－2)cm.14.【答案】B15.【答案】(1，－3)　[解析]由题意可得点P2(1，－1)，P3(－1，3)，P4(1，－3)，P5(1，3)，P6(－1，－1)，P7(1，1)，可知6个点一个循环，2020÷6＝336……4，故点P2020的坐标与点P4的坐标相同，为(1，－3)．三、解答题16.【答案】解：(1)证明：由题意可知，CD＝CE，∠DCE＝90°.∵∠ACB＝90°，∴∠ACB－∠DCB＝∠DCE－∠DCB， 即∠ACD＝∠BCE.在△ACD与△BCE中，∴△ACD≌△BCE(SAS)．(2)∵∠ACB＝90°，AC＝BC，∴∠A＝45°.∵△ACD≌△BCE，∴AD＝BE，∠CBE＝∠A＝45°.∵AD＝BF，∴BE＝BF，∴∠BEF＝×(180°－45°)＝67.5°.17.【答案】【思维教练】要作△ABC关于点O的中心对称图形，可先分别求出点A，B，C关于点O中心对称点，再顺次连接即可；(2)先作出点A′，再根据点A′在ΔA1B1C1，从而得出平移距离a满足A′A1