人教版初中数学九年级下册课件29.2 三视图 第3课时 由三视图确定几何体的面积或体积 19页

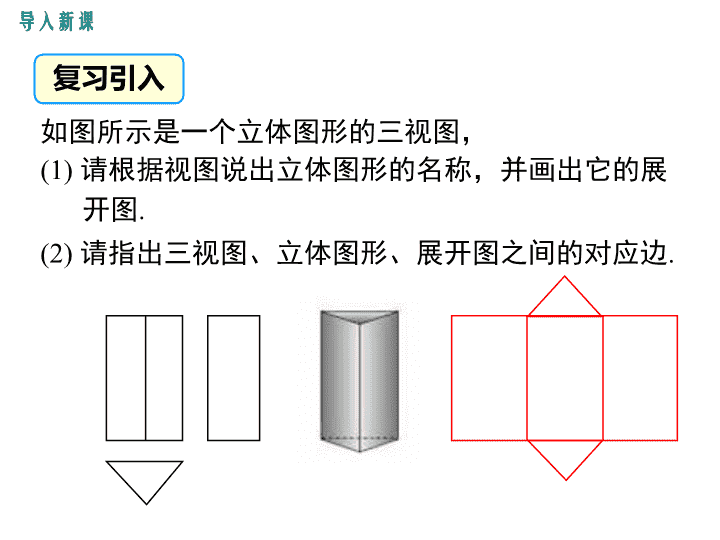
第二十九章投影与视图导入新课讲授新课当堂练习课堂小结29.2三视图第3课时由三视图确定几何体的面积或体积 1.能熟练地画出物体的三视图和由三视图想象出物体形状，进一步提高空间想象能力.(难点)2.由三视图想象出立体图形后能进行简单的面积或体积的计算.(重点)学习目标 导入新课如图所示是一个立体图形的三视图，(1)请根据视图说出立体图形的名称，并画出它的展开图.(2)请指出三视图、立体图形、展开图之间的对应边.复习引入 讲授新课三视图的有关计算分析：1.应先由三视图想象出；2.画出物体的.密封罐的立体形状展开图例1某工厂要加工一批密封罐，设计者给出了密封罐的三视图，请你按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位：mm).合作探究 解：由三视图可知，密封罐的形状是正六棱柱.50mm50mm密封罐的高为50mm，底面正六边形的直径为100mm，边长为50mm，100mm如图，是它的展开图. 由展开图可知，制作一个密封罐所需钢板的面积为 1.三种图形的转化：三视图立体图展开图2.由三视图求立体图形的面积的方法：(1)先根据给出的三视图确定立体图形，并确定立体图形的长、宽、高.(2)将立体图形展开成一个平面图形(展开图)，观察它的组成部分.(3)最后根据已知数据，求出展开图的面积.归纳： 主视图左视图俯视图8813如图是一个几何体的三视图．根据图示，可计算出该几何体的侧面积为．104π练一练 例2如图是一个几何体的三视图，根据所示数据，求该几何体的表面积和体积.分析：由三视图可知该几何体是由圆柱、长方体组合而成.分别计算它们的表面积和体积，然后相加即可. 解：该图形上、下部分分别是圆柱、长方体，根据图中数据得：表面积为20×32π+30×40×2+25×40×2+25×30×2=(5900+640π)(cm2),体积为25×30×40+102×32π=(30000+3200π)(cm3). 一个机器零件的三视图如图所示(单位：cm)，这个机器零件是一个什么样的立体图形？它的体积是多少？1510121510主视图左视图俯视图解：长方体，其体积为10×12×15=1800(cm3).练一练 1.一个长方体的左视图、俯视图及相关数据如图所示，则其主视图的面积为()A.6B.8C.12D.24当堂练习B 2.如图是一个几何体的三视图，根据图中提供的数据(单位：cm)，可求得这个几何体的体积为.3cm3主视图左视图俯视图311 3.如图是某几何体的三视图及相关数据(单位：cm)，则该几何体的侧面积为cm2.2π 4.如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图．(1)请写出构成这个几何体的正方体的个数为；(2)计算这个几何体的表面积为．520cm2 5.如图是一个几何体的三视图，试描绘出这个零件的形状，并求出此三视图所描述的几何体的表面积.解：该几何体的表面积为π×22+2π×2×2+1/2×4×4π=20π. 6.某一空间图形的三视图如图所示，其中主视图是半径为1的半圆以及高为1的矩形；左视图是半径为1的四分之一圆以及高为1的矩形；俯视图是半径为1的圆，求此图形的体积(参考公式：V球＝πR3)． 解：由已知可得该几何体是一个下部为圆柱，上部为1/4球的组合体．由三视图可得，下部圆柱的底面半径为1，高为1，则V圆柱＝π，上部1/4球的半径为1，则V1/4球＝π/3，故此几何体的体积为4π/3. 课堂小结1.三种图形的转化：2.由三视图求立体图形的体积(或面积)的方法：(1)先根据给出的三视图确定立体图形，并确定立体图形的长、宽、高、底面半径等；(2)根据已知数据，求出立体图形的体积(或将立体图形展开成一个平面图形，求出展开图的面积).三视图立体图展开图