2020-2021学年河南省鹤壁市淇滨区湘江中学八年级上学期第三次月考数学试卷 （解析版） 24页

2020-2021学年河南省鹤壁市淇滨区湘江中学八年级第一学期第三次月考数学试卷一、选择题1．（3分）下列运算正确的是（　　）A．（﹣a3）2＝a5B．（﹣a3）2＝﹣a6C．（﹣3a2）2＝6a4D．（﹣3a2）2＝9a42．（3分）下列说法正确的（　　）个．①0.09的算术平方根是0.03；②1的立方根是±1；③3.1＜＜3.2；④两边及一角分别相等的两个三角形全等．A．0B．1C．2D．33．（3分）（x2+ax+8）（x2﹣3x+b）展开式中不含x3和x2项，则a、b的值分别为（　　）A．a＝3，b＝1B．a＝﹣3，b＝1C．a＝0，b＝0D．a＝3，b＝84．（3分）已知a、b、c是△ABC的三条边，且满足a2+bc＝b2+ac，则△ABC是（　　）A．锐角三角形B．钝角三角形C．等腰三角形D．等边三角形5．（3分）下列尺规作图分别表示：①作一个角的平分线；②作一个角等于已知角；③作一条线段的垂直平分线．其中作法正确的是（　　）A．①②B．①③C．②③D．①②③6．（3分）下列命题中，假命题的是（　　）A．在△ABC中，若∠B+∠C＝∠A，则△ABC是直角三角形 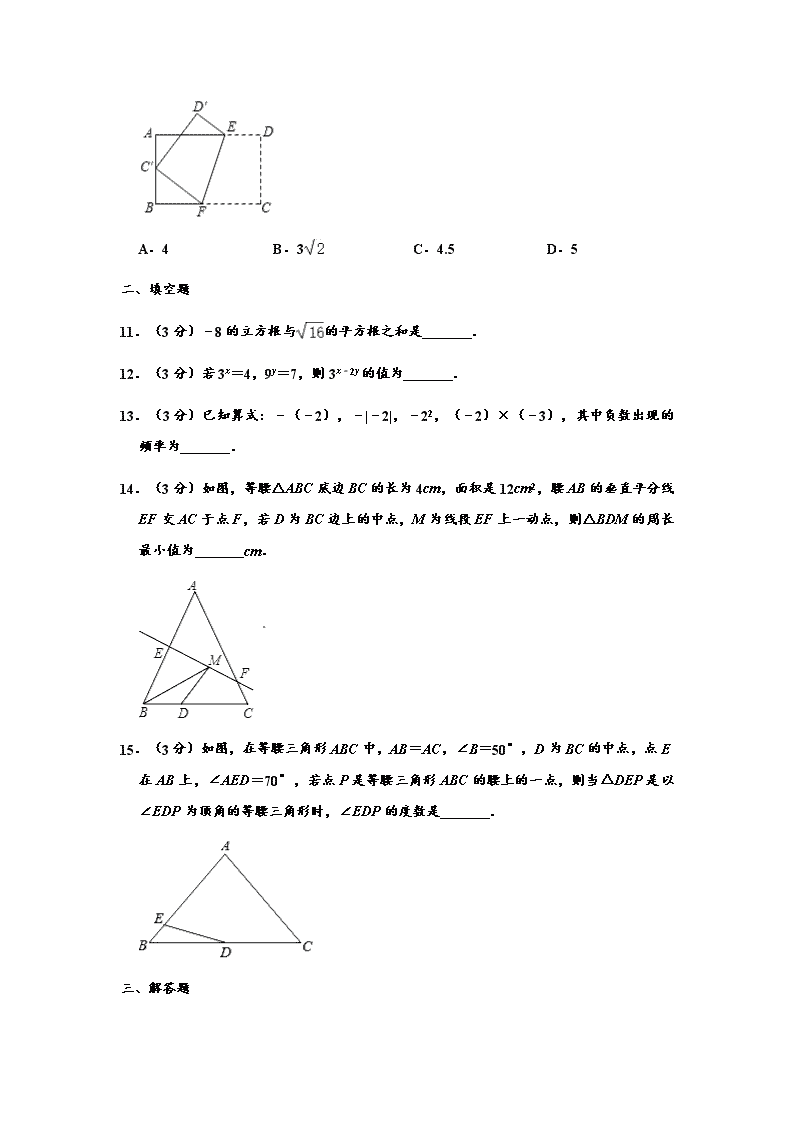B．在△ABC中，若a2＝（b+c）（b﹣c），则△ABC是直角三角形C．在△ABC中，若∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形D．在△ABC中，若a＝32，b＝42，c＝52，则△ABC是直角三角形7．（3分）如图，在△ABC中，∠C＝90°，∠B＝30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（　　）①AD平分∠BAC；②∠ADC＝60°；③点D在AB的垂直平分线上；④S△ABD＝2S△ACD．A．1B．2C．3D．48．（3分）已知AD是△ABC中BC边上的中线，若AB＝3，AD＝2，则AC的长可以是（　　）A．6B．7C．8D．99．（3分）已知直角三角形两边的长为3和4，则此三角形的周长为（　　）A．12B．7+C．12或7+D．以上都不对10．（3分）如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上．若AB＝6，BC＝9，则BF的长为（　　） A．4B．3C．4.5D．5二、填空题11．（3分）﹣8的立方根与的平方根之和是　　．12．（3分）若3x＝4，9y＝7，则3x﹣2y的值为　　．13．（3分）已知算式：﹣（﹣2），﹣|﹣2|，﹣22，（﹣2）×（﹣3），其中负数出现的频率为　　．14．（3分）如图，等腰△ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最小值为　　cm．15．（3分）如图，在等腰三角形ABC中，AB＝AC，∠B＝50°，D为BC的中点，点E在AB上，∠AED＝70°，若点P是等腰三角形ABC的腰上的一点，则当△DEP是以∠EDP为顶角的等腰三角形时，∠EDP的度数是　　．三、解答题 16．（8分）先化简，再求值．[（2a﹣1）2﹣（2a+1）（2a﹣1）+（2a﹣1）（a+2）]÷2a，其中a＝．17．（8分）计算：（1）；（2）（x﹣2y+3）（x+2y+3）．18．因式分解：（1）﹣3x2+6xy﹣3y2（2）a2（x﹣y）+16（y﹣x）19．（9分）学习了统计知识后，小明的数学老师要求每个学生就本班同学的上学方式进行一次调查统计，如图是小明通过收集数据后绘制的两幅不完整的统计图．请根据途中提供的信息，解答下列问题：（1）该班共有　　名学生；（2）将“骑自行车”部分的条形统计图补充完整；（3）在扇形统计图中，求出“乘车”部分所对应的圆心角的度数；（4）若全年级有600名学生，试估计该年级骑自行车上学的学生人数．20．（9分）如图，点C在BE上，AB⊥BE，DE⊥BE，且AB＝CE，AC＝CD．判断AC和CD的关系并说明理由． 21．（9分）如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF求证：AD平分∠BAC．22．（10分）如图所示的一块地ABCD，已知AD＝4m，CD＝3m，∠ADC＝90°，AB＝13m，BC＝12m，求这块地的面积．23．（11分）（1）作图发现如图1，已知△ABC，小涵同学以AB、AC为边向△ABC外作等边△ABD和等边△ACE．连接BE，CD．这时他发现BE与CD的数量关系是　　．（2）拓展探究如图2．已知△ABC，小涵同学以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，试判断BE与CD之间的数量关系，并说明理由．（3）解决问题如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC＝45°，∠CAE＝90°，AB＝BC＝200米．AC＝AE，则BE＝　　米． 24．（11分）“截长补短法”证明线段的和差问题：先阅读背景材料，猜想结论并填空，然后做问题探究．背景材料：（1）如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°．探究图中线段BE，EF，FD之间的数量关系．探究的方法是，延长FD到点G．使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出的结论是　　．探索问题：（2）如图2，若四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立？成立的话，请写出推理过程． 参考答案一、选择题1．（3分）下列运算正确的是（　　）A．（﹣a3）2＝a5B．（﹣a3）2＝﹣a6C．（﹣3a2）2＝6a4D．（﹣3a2）2＝9a4解：A、（﹣a3）2＝a6，故A选项错误；B、（﹣a3）2＝a6，故B选项错误；C、（﹣3a2）2＝9a4，故C选项错误；D、（﹣3a2）2＝9a4，故D选项正确；故选：D．2．（3分）下列说法正确的（　　）个．①0.09的算术平方根是0.03；②1的立方根是±1；③3.1＜＜3.2；④两边及一角分别相等的两个三角形全等．A．0B．1C．2D．3解：①0.09的算术平方根是0.3，不是0.03，因此①不正确；②1的立方根是1，不是±1，因此②不正确；③因为3.12＝9.91，3.22＝10.24，而9.91＜10＜10.24，所以3.1＜＜3.2，因此③正确；④只有两边夹角对应相等的两个三角形全等，而两边及一角分别相等的两个三角形不一定全等．因此④不正确；所以正确的只有③，故选：B． 3．（3分）（x2+ax+8）（x2﹣3x+b）展开式中不含x3和x2项，则a、b的值分别为（　　）A．a＝3，b＝1B．a＝﹣3，b＝1C．a＝0，b＝0D．a＝3，b＝8解：（x2+ax+8）（x2﹣3x+b）＝x4﹣3x3+bx2+ax3﹣3ax2+abx+8x2﹣24x+8b＝x4+（﹣3+a）x3+（b﹣3a+8）x2+（ab﹣24）x+8b，由展开式中不含x3和x2项，得到﹣3+a＝0，b﹣3a+8＝0，解得：a＝3，b＝1．故选：A．4．（3分）已知a、b、c是△ABC的三条边，且满足a2+bc＝b2+ac，则△ABC是（　　）A．锐角三角形B．钝角三角形C．等腰三角形D．等边三角形解：已知等式变形得：（a+b）（a﹣b）﹣c（a﹣b）＝0，即（a﹣b）（a+b﹣c）＝0，∵a+b﹣c≠0，∴a﹣b＝0，即a＝b，则△ABC为等腰三角形．故选：C．5．（3分）下列尺规作图分别表示：①作一个角的平分线；②作一个角等于已知角；③作一条线段的垂直平分线．其中作法正确的是（　　）A．①②B．①③C．②③D．①②③解：①作一个角的平分线的作法正确；②作一个角等于已知角的方法正确； ③作一条线段的垂直平分线，缺少另一个交点，故作法错误；故选：A．6．（3分）下列命题中，假命题的是（　　）A．在△ABC中，若∠B+∠C＝∠A，则△ABC是直角三角形B．在△ABC中，若a2＝（b+c）（b﹣c），则△ABC是直角三角形C．在△ABC中，若∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形D．在△ABC中，若a＝32，b＝42，c＝52，则△ABC是直角三角形解：A、在△ABC中，若∠B+∠C＝∠A，∠A＝90°，则△ABC是直角三角形，正确不符合题意；B、在△ABC中，若a2＝（b+c）（b﹣c），则△ABC是直角三角形，正确不符合题意；C、在△ABC中，若∠A：∠B：∠C＝1：2：3，∴∠A＝90°，正确不符合题意；D、在△ABC中，若a＝32，b＝42，c＝52，则△ABC不是直角三角形，错误符合题意；故选：D．7．（3分）如图，在△ABC中，∠C＝90°，∠B＝30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（　　）①AD平分∠BAC；②∠ADC＝60°；③点D在AB的垂直平分线上；④S△ABD＝2S△ACD． A．1B．2C．3D．4解：∵∠C＝90°，∠B＝30°，∴∠BAC＝60°，由作法得AD平分∠BAC，所以①正确；∴∠BAD＝∠CAD＝30°，∴∠ADC＝90°﹣∠CAD＝60°，所以②正确；∵∠B＝∠BAD，∴DA＝DB，∴点D在AB的垂直平分线上，所以③正确；∵如图，在直角△ACD中，∠CAD＝30°，∴CD＝AD，∴BC＝CD+BD＝AD+AD＝AD，S△DAC＝AC•CD＝AC•AD．∴S△ABC＝AC•BC＝AC•AD＝AC•AD，∴S△DAC：S△ABC＝AC•AD：AC•AD＝1：3，∴S△DAC：S△ABD＝1：2．即S△ABD＝2S△ACD，故④正确．故选：D．8．（3分）已知AD是△ABC中BC边上的中线，若AB＝3，AD＝2，则AC的长可以是（　　） A．6B．7C．8D．9解：延长AD至E，使DE＝AD，连接CE．∵BD＝CD，∠ADB＝∠EDC，AD＝DE，∴△ABD≌△ECD，∴CE＝AB．在△ACE中，CE﹣AC＜AE＜CE+AC，即3﹣AC＜4＜3+AC，∴1＜AC＜7．故选：A．9．（3分）已知直角三角形两边的长为3和4，则此三角形的周长为（　　）A．12B．7+C．12或7+D．以上都不对解：设Rt△ABC的第三边长为x，①当4为直角三角形的直角边时，x为斜边，由勾股定理得，x＝5，此时这个三角形的周长＝3+4+5＝12；②当4为直角三角形的斜边时，x为直角边，由勾股定理得，x＝，此时这个三角形的周长＝3+4+，故选：C．10．（3分）如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C ′上．若AB＝6，BC＝9，则BF的长为（　　）A．4B．3C．4.5D．5解：∵点C′是AB边的中点，AB＝6，∴BC′＝3，由图形折叠特性知，C′F＝CF＝BC﹣BF＝9﹣BF，在Rt△C′BF中，BF2+BC′2＝C′F2，∴BF2+9＝（9﹣BF）2，解得，BF＝4，故选：A．二、填空题11．（3分）﹣8的立方根与的平方根之和是　0或﹣4　．解：∵﹣8的立方根为﹣2、的平方根为2或﹣2，∴﹣8的立方根与的平方根之和是﹣2+2＝0或﹣2﹣2＝﹣4，故答案为：0或﹣4．12．（3分）若3x＝4，9y＝7，则3x﹣2y的值为　　．解：3x﹣2y＝3x÷32y＝3x÷9y＝．故答案是：．13．（3分）已知算式：﹣（﹣2），﹣|﹣2|，﹣22 ，（﹣2）×（﹣3），其中负数出现的频率为　0.5　．解：∵﹣（﹣2）＝2，﹣|﹣2|＝﹣2，﹣22＝﹣4，（﹣2）×（﹣3）＝6，∴这些数中负数有：﹣|﹣2|，﹣22，∴负数出现的频数为2，∴负数出现的频率＝2÷4＝0.5．故答案为：0.5．14．（3分）如图，等腰△ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最小值为　8　cm．解：连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC＝BC•AD＝×4×AD＝12，解得AD＝6cm，∵EF是线段AB的垂直平分线，∴点B关于直线EF的对称点为点A，∴AD的长为BM+MD的最小值，∴△BDM的周长最短＝（BM+MD）+BD＝AD+BC＝6+×4＝6+2＝8cm．故答案为：8． 15．（3分）如图，在等腰三角形ABC中，AB＝AC，∠B＝50°，D为BC的中点，点E在AB上，∠AED＝70°，若点P是等腰三角形ABC的腰上的一点，则当△DEP是以∠EDP为顶角的等腰三角形时，∠EDP的度数是　40°或100°或140°　．解：∵AB＝AC，∠B＝50°，∠AED＝70°，∴∠EDB＝20°，∵当△DEP是以∠EDP为顶角的等腰三角形，当点P在AB上，∵DE＝DP1，∴∠DP1E＝∠AED＝70°，∴∠EDP1＝180°﹣70°﹣70°＝40°，当点P在AC上，∵AB＝AC，D为BC的中点，∴∠BAD＝∠CAD，过D作DG⊥AB于G，DH⊥AC于H，∴DG＝DH， 在Rt△DEG与Rt△DP2H中，，∴Rt△DEG≌Rt△DP2H（HL），∴∠AP2D＝∠AED＝70°，∵∠BAC＝180°﹣50°﹣50°，∴∠EDP2＝140°，当点P在AC上，同理证得Rt△DEG≌Rt△DPH（HL），∴∠EDG＝∠P3DH，∴∠EDP3＝∠GDH＝100°，故答案为：40°或100°或140°．三、解答题16．（8分）先化简，再求值．[（2a﹣1）2﹣（2a+1）（2a﹣1）+（2a﹣1）（a+2）]÷2a，其中a＝．解：[（2a﹣1）2﹣（2a+1）（2a﹣1）+（2a﹣1）（a+2）]÷2a＝[4a2﹣4a+1﹣4a2+1+2a2+4a﹣a﹣2]÷2a＝[2a2﹣a]÷2a＝a﹣， 当a＝时，原式＝0．17．（8分）计算：（1）；（2）（x﹣2y+3）（x+2y+3）．解：（1）原式＝2+（﹣1）++5＝6+＝；（2）原式＝（x+3﹣2y）（x+3+2y）＝（x+3）2﹣4y2＝x2+6x+9﹣4y2．18．因式分解：（1）﹣3x2+6xy﹣3y2（2）a2（x﹣y）+16（y﹣x）解：（1）﹣3x2+6xy﹣3y2＝﹣3（x2﹣2xy+y2）＝﹣3（x﹣y）2；（2）a2（x﹣y）+16（y﹣x）＝（x﹣y）（a2﹣16）＝（x﹣y）（a+4）（a﹣4）． 19．（9分）学习了统计知识后，小明的数学老师要求每个学生就本班同学的上学方式进行一次调查统计，如图是小明通过收集数据后绘制的两幅不完整的统计图．请根据途中提供的信息，解答下列问题：（1）该班共有　40　名学生；（2）将“骑自行车”部分的条形统计图补充完整；（3）在扇形统计图中，求出“乘车”部分所对应的圆心角的度数；（4）若全年级有600名学生，试估计该年级骑自行车上学的学生人数．解：（1）20÷50%＝40；故答案为：40；（2）骑自行车的人数为：20%×40＝8（人），如图所示：（3）“乘车”部分所对应的圆心角的度数为360×＝108°；（4）600×20%＝120人． 所以估计该年级骑自行车上学的学生人数为120人．20．（9分）如图，点C在BE上，AB⊥BE，DE⊥BE，且AB＝CE，AC＝CD．判断AC和CD的关系并说明理由．解：AC⊥CD．理由：∵AB⊥BE，DE⊥BE，∴∠B＝∠E＝90°．在Rt△ABC和Rt△CED中，，∴Rt△ABC≌Rt△CED（HL），∴∠A＝∠DCE，∠ACB＝∠D．∵∠A+∠ACB＝90°，∴∠DCE+∠ACB＝90°．∵∠DCE+∠ACB+∠ACD＝180°，∴∠ACD＝90°，∴AC⊥CD．21．（9分）如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF求证：AD平分∠BAC． 【解答】证明：∵DE⊥AB，DF⊥AC，∴∠E＝∠DFC＝90°，在Rt△BDE和Rt△CDF中，，∴Rt△BDE≌Rt△CDF（HL），∴DE＝DF，∴AD平分∠BAC．22．（10分）如图所示的一块地ABCD，已知AD＝4m，CD＝3m，∠ADC＝90°，AB＝13m，BC＝12m，求这块地的面积．解：连接AC，∵∠ADC＝90°，AD＝4，CD＝3，∴AC2＝AD2+CD2＝42+32＝25，又∵AC＞0，∴AC＝5，又∵BC＝12，AB＝13，∴AC2+BC2＝52+122＝169， 又∵AB2＝169，∴AC2+BC2＝AB2，∴∠ACB＝90°，∴S四边形ABCD＝S△ABC﹣S△ADC＝30﹣6＝24m2．23．（11分）（1）作图发现如图1，已知△ABC，小涵同学以AB、AC为边向△ABC外作等边△ABD和等边△ACE．连接BE，CD．这时他发现BE与CD的数量关系是　相等　．（2）拓展探究如图2．已知△ABC，小涵同学以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，试判断BE与CD之间的数量关系，并说明理由．（3）解决问题如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC＝45°，∠CAE＝90°，AB＝BC＝200米．AC＝AE，则BE＝　200　米．解：（1）如图1所示：∵△ABD和△ACE都是等边三角形，∴AD＝AB，AC＝AE，∠BAD＝∠CAE＝60°， ∴∠BAD+∠BAC＝∠CAE+∠BAC，即∠CAD＝∠EAB，在△CAD和△EAB中，∵，∴△CAD≌△EAB（SAS），∴BE＝CD；（2）BE＝CD，理由同（1），∵四边形ABFD和ACGE均为正方形，∴AD＝AB，AC＝AE，∠BAD＝∠CAE＝90°，∴∠CAD＝∠EAB，∵在△CAD和△EAB中，，∴△CAD≌△EAB（SAS），∴BE＝CD；（3）如图3，由（1）、（2）的解题经验可知，过A作等腰直角△ABD，∠BAD＝90°，则AD＝AB＝200米，∠ABD＝45°，∴BD＝200米，连接CD，BD，则由（2）可得BE＝CD，∵∠ABC＝45°，∴∠DBC＝90°， 在Rt△DBC中，BC＝200米，BD＝200米，根据勾股定理得：CD＝＝200（米），则BE＝CD＝200米．故答案为：200．24．（11分）“截长补短法”证明线段的和差问题：先阅读背景材料，猜想结论并填空，然后做问题探究．背景材料：（1）如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°．探究图中线段BE，EF，FD之间的数量关系．探究的方法是，延长FD到点G．使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出的结论是　EF＝BE+FD　．探索问题：（2）如图2，若四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立？成立的话，请写出推理过程． 【解答】证明：（1）在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝∠BAD，∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，∴∠EAF＝∠GAF，在△AEF和△GAF中，，∴△AEF≌△AGF（SAS），∴EF＝FG，∵FG＝DG+DF＝BE+DF，∴EF＝BE+DF；故答案为：EF＝BE+DF．（2）解：结论EF＝BE+DF仍然成立；理由：延长FD到点G．使DG＝BE．连结AG， 在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝∠BAD，∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，∴∠EAF＝∠GAF，在△AEF和△GAF中，，∴△AEF≌△AGF（SAS），∴EF＝FG，∵FG＝DG+DF＝BE+DF，∴EF＝BE+DF．