华东师大版数学中考专题复习与训练课件-第1篇 第4章 4解直角三角形 69页

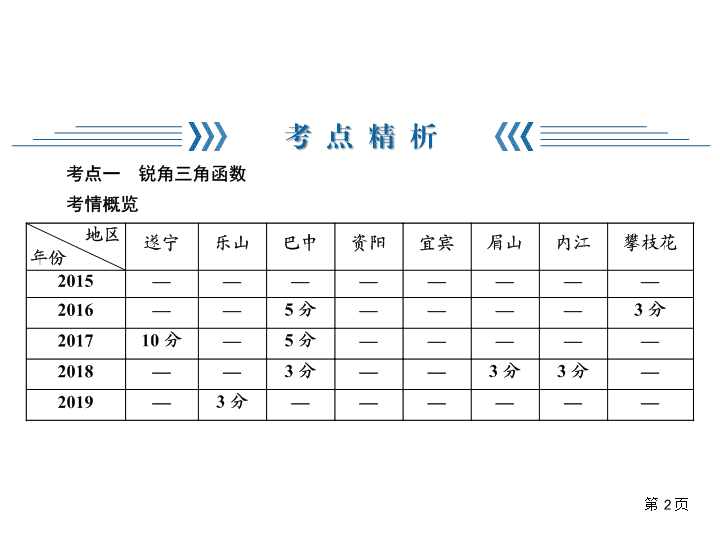
第一篇过教材·考点透析第四章　三角形4.6解直角三角形 第2页考点精析 1．锐角三角函数的意义如图，在Rt△ABC中，∠C＝90°，则锐角∠A的三角函数可定义如下：(1)∠A的正弦：sinA＝①______；(2)∠A的余弦：cosA＝②______；(3)∠A的正切：tanA＝③______.第3页易错提示：(1)三角函数sinA、cosA、tanA的记法里习惯省去角的符号“∠”．(2)三角函数没有单位，它表示两条线段长度的比值． 2．互余两角的三角函数关系sinα＝cos(90°－α)；cosα＝sin(90°－α)．第4页方法点拨：在研究锐角三角函数时，我们都是把这些锐角放到直角三角形中来研究的，如果没有直角三角形，我们要设法构造适当的直角三角形． 第5页1 第6页 1．解直角三角形的含义在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角．由直角三角形中除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形．2．解直角三角形时常用的基本关系如图，在△ABC中，∠C为直角，∠A、∠B、∠C所对的边分别为a、b、c，则有：(1)三边之间的关系(勾股定理)：⑩______________；(2)两锐角之间的关系：⑪____________________；第7页a2＋b2＝c2∠A＋∠B＝90° 第8页 第9页 第10页 1．解直角三角形的应用中的几个名词及相关概念(1)仰角与俯角：如图，当从低处观测高处的目标时，视线与水平线所成的锐角称为⑫________；当从高处观测低处的目标时，视线与水平线所成的锐角称为⑬________.第11页仰角俯角 第12页坡角坡度坡比 (3)方向角：从某点指北或指南方向线与目标方向线所成的小于⑰________的水平夹角，叫做方向角．如图，OA、OB、OC、OD的方向角分别是：北偏东30°、南偏东45°(东南方向)、南偏西60°、北偏西60°.第13页90° 2．应用解直角三角形解决实际问题的思路(1)如果有直角三角形，利用直角三角形中边角之间的关系求解即可．(2)如果没有直角三角形，先构造直角三角形，再用直角三角形边角之间的关系求解．第14页 3．解直角三角形应用题的一般步骤解直角三角形的实际应用主要涉及测量、航空、航海、工程等领域，解此类问题一般按以下步骤进行：(1)根据题中图形标出已知长度和角度，以及待求长度或高度；(2)构造直角三角形，一般根据题中图形，作出合适的高．如果题中图形是三角形，一般采用切割法或拼补法构造两个直角三角形，如图1.如果题中图形是梯形，一般构造直角三角形和矩形，如图2；第15页 第16页 第17页四川中考真题精练C 第18页D 第19页D 第20页90°2 第21页D 第22页 第23页 第24页A 第25页B 第26页B 第27页 14．(2019·宜宾中考)如图，为了测得某建筑物的高度AB，在C处用高为1米的测角仪CF，测得该建筑物顶端A的仰角为45°，再向建筑物方向前进40米，又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB．(结果保留根号)第28页 15．(2019·内江中考)如图，两座建筑物DA与CB，其中CB的高为120米，从DA的顶点A测得CB顶部B的仰角为30°，测得其底部C的俯角为45°，求这两座建筑物的地面距离DC为多少米？(结果保留根号)第29页 第30页 16．(2019·成都中考)2019年，成都马拉松成为世界马拉松大满贯联盟的候选赛事，这大幅度提升了成都市的国际影响力．如图，在一场马拉松比赛中，某人在大楼A处，测得起点拱门CD的顶部C的俯角为35°，底部D的俯角为45°，如果A处离地面的高度AB＝20米，求起点拱门CD的高度．(结果精确到1米，参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70)第31页 第32页 17．(2018·巴中中考)在一次课外活动中，甲、乙两位同学测量公园中孔子塑像的高度．他们分别在A、B两处用高度为1.5m的测角仪测得塑像顶部C的仰角分别为30°，45°，两人间的水平距离AB为10m，求塑像的高度CF.(结果保留根号)第33页 第34页 第35页 第36页 第37页 20．(2017·广安中考)如图，线段AB、CD分别表示甲、乙两建筑物的高，BA⊥AD，CD⊥DA，垂足分别为A、D．从点D测到点B的仰角α为60°，从点C测得点B的仰角β为30°，甲建筑物的高AB＝30米．(1)求甲、乙两建筑物之间的距离AD；(2)求乙建筑物的高CD．第38页 第39页 21．(2017·泸州中考)如图，海中一渔船在A处且与小岛C相距70nmile，若该渔船由西向东航行30nmile到达B处，此时测得小岛C位于B的北偏东30°方向上．求该渔船此时与小岛C之间的距离．第40页 第41页 第42页A 23．(2019·安徽中考)筒车是我国古代发明的一种水利灌溉工具．如图1，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理．如图2，筒车盛水桶的运行轨迹是以轴心O为圆心的圆．已知圆心在水面上方，且圆被水面截得的弦AB长为6米，∠OAB＝41.3°，若点C为运行轨道的最高点(C、O的连线垂直于AB)，求点C到弦AB所在直线的距离．(参考数据：sin41.3°≈0.66，cos41.3°≈0.75，tan41.3°≈0.88)第43页 第44页 24．(2019·甘肃兰州中考)某数学课题研究小组针对兰州市住房“如何设计遮阳篷”这一课题进行了探究．过程如下：问题提出：第45页如图1是某住户上方安装的遮阳篷，要求设计的遮阳篷既能最大限度地遮挡夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内．方案设计：如图2，该数学课题研究小组通过调查研究设计了垂直于墙面AC的遮阳篷CD． 第46页 第47页 突破点一　锐角三角函数(2019·湖北宜昌中考)如图，在5×4的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，则sin∠BAC的值为()第48页重难突破D 解题技巧：解答此题的关键是通过作辅助线，构造出直角三角形，再利用锐角三角函数定义及勾股定理求三角函数值．第49页 第50页 解题技巧：本题考查了解直角三角形的性质及平行线的性质，解答此题的关键是根据题意构造直角三角形，再利用所学的三角函数的关系进行解答．第51页 第52页 解题技巧：对于解直角三角形的应用，解题的关键是将实际问题转化为解直角三角形问题，建立直角三角形模型，由题意得出数据，然后求解．第53页 第54页2020年迎考特训D 2．(湖北宜昌中考)如图，要测量小河两岸相对的两点P、A的距离，可以在小河边取PA的垂线PB上的一点C，测得PC＝100米，∠PCA＝35°，则小河宽PA等于()A．100sin35°米B．100sin55°米C．100tan35°米D．100tan55°米第55页C 第56页D 第57页 第58页没有超速 第59页 第60页54.6 10．(2019·山东德州中考)如图，一架长为6米的梯子AB斜靠在一竖直的墙AO上，这时测得∠ABO＝70°，如果梯子的底端B外移到D，则梯子顶端A下移到C，这时又测得∠CDO＝50°，那么AC的长度约为________米．(sin70°≈0.94，sin50°≈0.77，cos70°≈0.34，cos50°≈0.64)第61页1.0211．(江苏无锡中考)已知△ABC中，AB＝10，AC＝2，∠B＝30°，则△ABC的面积等于______________． 第62页 第63页 13．(2017·四川眉山中考)如图，为了测量一棵树的高度AB，小明在D处用高为1m的测角仪CD，测得树顶A的仰角为45°，再向树方向前进10m，又测得树顶A的仰角为60°，求这棵树的高度AB．第64页 第65页 14．(2017·四川内江中考)如图，某人为了测量小山顶上的塔ED的高，他在山下的点A处测得塔尖点D的仰角为45°，再沿AC方向前进60m到达山脚点B，测得塔尖点D的仰角为60°，塔底点E的仰角为30°，求塔ED的高度．(结果保留根号)第66页 第67页 15．(2017·四川凉山中考)如图，若要在宽AD为20米的城南大道两边安装路灯，路灯的灯臂BC长2米，且与灯柱AB成120°角，路灯采用圆锥形灯罩，灯罩的轴线CO与灯臂BC垂直，当灯罩的轴线CO通过公路路面的中心线时照明效果最好，此时，路灯的灯柱高AB应该设计为多少米？(结果保留根号)第68页 第69页