2020年贵州省贵阳市中考数学试卷 34页

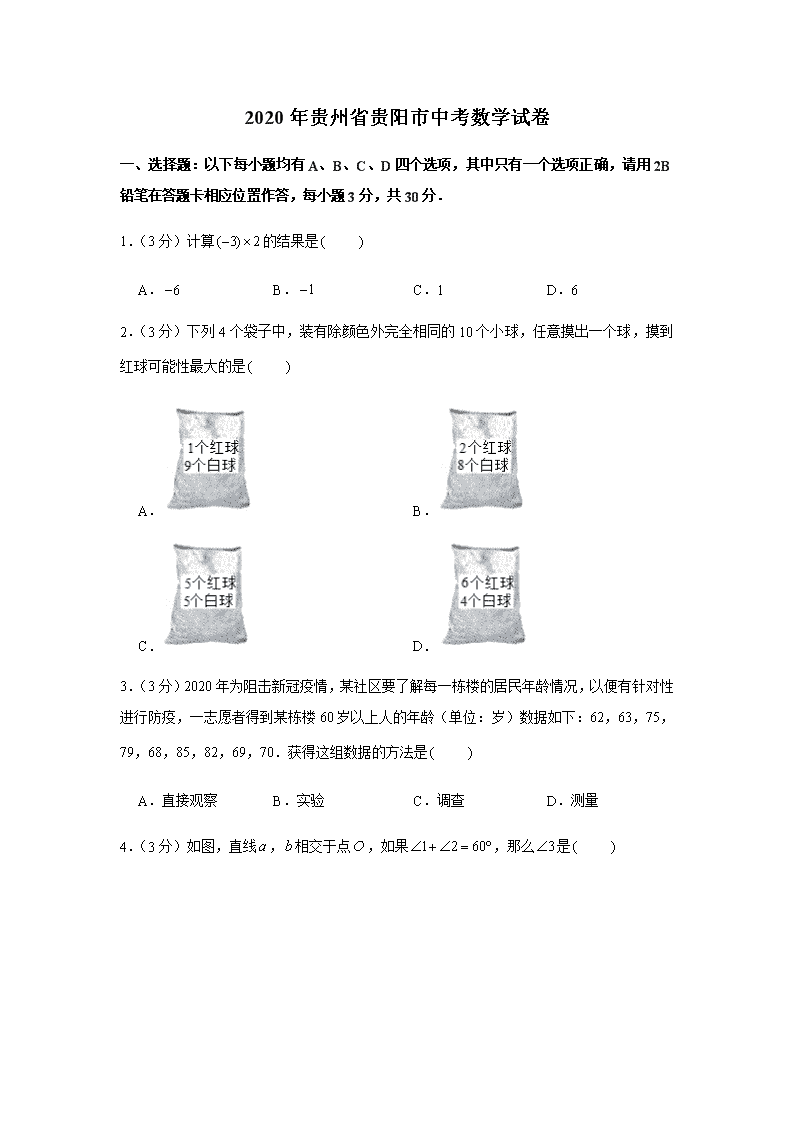
2020年贵州省贵阳市中考数学试卷一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答，每小题3分，共30分．1．（3分）计算的结果是　　A．B．C．1D．62．（3分）下列4个袋子中，装有除颜色外完全相同的10个小球，任意摸出一个球，摸到红球可能性最大的是　　A．B．C．D．3．（3分）2020年为阻击新冠疫情，某社区要了解每一栋楼的居民年龄情况，以便有针对性进行防疫，一志愿者得到某栋楼60岁以上人的年龄（单位：岁）数据如下：62，63，75，79，68，85，82，69，70．获得这组数据的方法是　　A．直接观察B．实验C．调查D．测量4．（3分）如图，直线，相交于点，如果，那么是　　 A．B．C．D．5．（3分）当时，下列分式没有意义的是　　A．B．C．D．6．（3分）下列四幅图中，能表示两棵树在同一时刻太阳光下的影子的图是　　A．B．C．D．7．（3分）菱形的两条对角线长分别是6和8，则此菱形的周长是　　A．5B．20C．24D．328．（3分）已知，下列式子不一定成立的是　　A．B．C．D．9．（3分）如图，中，，利用尺规在，上分别截取，，使 ；分别以，为圆心、以大于的长为半径作弧，两弧在内交于点；作射线交于点．若，为上一动点，则的最小值为　　A．无法确定B．C．1D．210．（3分）已知二次函数的图象经过与两点，关于的方程有两个根，其中一个根是3．则关于的方程有两个整数根，这两个整数根是　　A．或0B．或2C．或3D．或4二、填空题：每小题4分，共20分．11．（4分）化简的结果是　　．12．（4分）如图，点是反比例函数图象上任意一点，过点分别作轴，轴的垂线，垂足为，，则四边形的面积为　　．13．（4分）在“抛掷正六面体”的试验中，正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”，在试验次数很大时，数字“6”朝上的频率的变化趋势接近的值是　　．14．（4分）如图，是的内接正三角形，点是圆心，点，分别在边， 上，若，则的度数是　　度．15．（4分）如图，中，点在边上，，，垂直于的延长线于点，，，则边的长为　　．三、解答题：本大题10小题，共100分．16．（8分）如图，在的正方形网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．（1）在图①中，画一个直角三角形，使它的三边长都是有理数；（2）在图②中，画一个直角三角形，使它的一边长是有理数，另外两边长是无理数；（3）在图③中，画一个直角三角形，使它的三边长都是无理数．17．（10分）2020年2 月，贵州省积极响应国家“停课不停学”的号召，推出了“空中黔课”．为了解某中学初三学生每天听空中黔课的时间，随机调查了该校部分初三学生．根据调查结果，绘制出了如图统计图表（不完整），请根据相关信息，解答下列问题：部分初三学生每天听空中黔课时间的人数统计表时间1.522.533.54人数人266104（1）本次共调查的学生人数为　　，在表格中，　　；（2）统计的这组数据中，每天听空中黔课时间的中位数是　　，众数是　　；（3）请就疫情期间如何学习的问题写出一条你的看法．18．（10分）如图，四边形是矩形，是边上一点，点在的延长线上，且．（1）求证：四边形是平行四边形；（2）连接，若，，，求四边形的面积．19．（10分）如图，一次函数的图象与反比例函数的图象相交，其中一个交点的横坐标是2． （1）求反比例函数的表达式；（2）将一次函数的图象向下平移2个单位，求平移后的图象与反比例函数图象的交点坐标；（3）直接写出一个一次函数，使其过点，且与反比例函数的图象没有公共点．20．（10分）“2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动，规则是：准备3张大小一样，背面完全相同的卡片，3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》，将它们背面朝上洗匀后任意抽出一张，抽到卡片后可以免费领取卡片上相应的书籍．（1）在上面的活动中，如果从中随机抽出一张卡片，记下内容后不放回，再随机抽出一张卡片，请用列表或画树状图的方法，求恰好抽到2张卡片都是《辞海》的概率；（2）再添加几张和原来一样的《消防知识手册》卡片，将所有卡片背面朝上洗匀后，任意抽出一张，使得抽到《消防知识手册》卡片的概率为，那么应添加多少张《消防知识手册》卡片？请说明理由．21．（8分）脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高所在的直线，为了测量房屋的高度，在地面上点测得屋顶的仰角为，此时地面上点、屋檐上点、屋顶上点三点恰好共线，继续向房屋方向走到达点时，又测得屋檐点的仰角为，房屋的顶层横梁，，交于点（点，，在同一水平线上）．（参考数据：，，， （1）求屋顶到横梁的距离；（2）求房屋的高（结果精确到．22．（10分）第33个国际禁毒日到来之际，贵阳市策划了以“健康人生绿色无毒”为主题的禁毒宣传月活动，某班开展了此项活动的知识竞赛．学习委员为班级购买奖品后与生活委员对话如下：（1）请用方程的知识帮助学习委员计算一下，为什么说学习委员搞错了；（2）学习委员连忙拿出发票，发现的确错了，因为他还买了一本笔记本，但笔记本的单价已模糊不清，只能辨认出单价是小于10元的整数，那么笔记本的单价可能是多少元？23．（10分）如图，为的直径，四边形内接于，对角线，交于点，的切线交的延长线于点，切点为，且．（1）求证：；（2）若，，求的值． 24．（12分）2020年体育中考，增设了考生进入考点需进行体温检测的要求．防疫部门为了解学生错峰进入考点进行体温检测的情况，调查了一所学校某天上午考生进入考点的累计人数（人与时间（分钟）的变化情况，数据如下表：（表中表示时间（分钟）0123456789人数（人0170320450560650720770800810810（1）根据这15分钟内考生进入考点的累计人数与时间的变化规律，利用初中所学函数知识求出与之间的函数关系式；（2）如果考生一进考点就开始测量体温，体温检测点有2个，每个检测点每分钟检测20人，考生排队测量体温，求排队人数最多时有多少人？全部考生都完成体温检测需要多少时间？（3）在（2）的条件下，如果要在12分钟内让全部考生完成体温检测，从一开始就应该至少增加几个检测点？25．（12分）如图，四边形是正方形，点为对角线的中点．（1）问题解决：如图①，连接，分别取，的中点，，连接，则与的数量关系是　　，位置关系是　　；（2）问题探究：如图②，△是将图①中的绕点按顺时针方向旋转得到的三角形，连接，点，分别为，的中点，连接，．判断的形状，并证明你的结论；（3）拓展延伸：如图③，△是将图①中的绕点按逆时针方向旋转得到的三角形，连接，点，分别为，的中点，连接，．若正方形 的边长为1，求的面积． 2020年贵州省贵阳市中考数学试卷参考答案与试题解析一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答，每小题3分，共30分．1．（3分）计算的结果是　　A．B．C．1D．6【解答】解：原式．故选：．2．（3分）下列4个袋子中，装有除颜色外完全相同的10个小球，任意摸出一个球，摸到红球可能性最大的是　　A．B．C．D．【解答】解：在四个选项中，选项袋子中红球的个数最多，所以从选项袋子中任意摸出一个球，摸到红球可能性最大，故选：．3．（3分）2020年为阻击新冠疫情，某社区要了解每一栋楼的居民年龄情况，以便有针对性进行防疫，一志愿者得到某栋楼60岁以上人的年龄（单位：岁）数据如下：62，63，75， 79，68，85，82，69，70．获得这组数据的方法是　　A．直接观察B．实验C．调查D．测量【解答】解：一志愿者得到某栋楼60岁以上人的年龄（单位：岁）数据如下：62，63，75，79，68，85，82，69，70．获得这组数据的方法是：调查．故选：．4．（3分）如图，直线，相交于点，如果，那么是　　A．B．C．D．【解答】解：，（对顶角相等），，与互为邻补角，．故选：．5．（3分）当时，下列分式没有意义的是　　A．B．C．D．【解答】解：、，当时，分式有意义不合题意； 、，当时，，分式无意义符合题意；、，当时，分式有意义不合题意；、，当时，分式有意义不合题意；故选：．6．（3分）下列四幅图中，能表示两棵树在同一时刻太阳光下的影子的图是　　A．B．C．D．【解答】解：、两棵小树的影子的方向相反，不可能为同一时刻阳光下影子，所以选项错误；、两棵小树的影子的方向相反，不可能为同一时刻阳光下影子，所以选项错误；、在同一时刻阳光下，树高与影子成正比，所以选项正确．、图中树高与影子成反比，而在同一时刻阳光下，树高与影子成正比，所以选项错误；故选：．7．（3分）菱形的两条对角线长分别是6和8，则此菱形的周长是　　A．5B．20C．24D．32【解答】解：如图所示：四边形是菱形，，， ，，，，，此菱形的周长；故选：．8．（3分）已知，下列式子不一定成立的是　　A．B．C．D．【解答】解：、在不等式的两边同时减去1，不等号的方向不变，即，原变形正确，故此选项不符合题意；、在不等式的两边同时乘以，不等号方向改变，即，原变形正确，故此选项不符合题意；、在不等式的两边同时乘以，不等号的方向不变，即，不等式的两边同时加上1，不等号的方向不变，即，原变形正确，故此选项不符合题意；、在不等式的两边同时乘以，不等式不一定成立，即，或，或，原变形不正确，故此选项符合题意．故选：．9．（3分）如图，中，，利用尺规在，上分别截取，，使；分别以，为圆心、以大于的长为半径作弧，两弧在内交于点；作射线交于点．若，为上一动点，则的最小值为　　 A．无法确定B．C．1D．2【解答】解：如图，过点作于．由作图可知，平分，，，，根据垂线段最短可知，的最小值为1，故选：．10．（3分）已知二次函数的图象经过与两点，关于的方程有两个根，其中一个根是3．则关于的方程有两个整数根，这两个整数根是　　A．或0B．或2C．或3D．或4【解答】解：二次函数的图象经过与两点，当时，的两个根为和1，函数的对称轴是直线，又关于的方程有两个根，其中一个根是3． 方程的另一个根为，函数的图象开口向上，关于的方程有两个整数根，这两个整数根是或2，故选：．二、填空题：每小题4分，共20分．11．（4分）化简的结果是　　．【解答】解：，故答案为：．12．（4分）如图，点是反比例函数图象上任意一点，过点分别作轴，轴的垂线，垂足为，，则四边形的面积为　3　．【解答】解：过点分别作轴，轴的垂线，垂足为，，，则四边形的面积为：3．故答案为：3． 13．（4分）在“抛掷正六面体”的试验中，正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”，在试验次数很大时，数字“6”朝上的频率的变化趋势接近的值是　　．【解答】解：在试验次数很大时，数字“6”朝上的频率的变化趋势接近的值是．故答案为：．14．（4分）如图，是的内接正三角形，点是圆心，点，分别在边，上，若，则的度数是　120　度．【解答】解：连接，，是的内接正三角形，，，，，，，，，， ，故答案为：120．15．（4分）如图，中，点在边上，，，垂直于的延长线于点，，，则边的长为　　．【解答】解：延长到，使得，，是等腰三角形，，过点点作，交于点，，，，，， 在，由勾股定理可知：，在中，，故答案为：三、解答题：本大题10小题，共100分．16．（8分）如图，在的正方形网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．（1）在图①中，画一个直角三角形，使它的三边长都是有理数；（2）在图②中，画一个直角三角形，使它的一边长是有理数，另外两边长是无理数；（3）在图③中，画一个直角三角形，使它的三边长都是无理数． 【解答】解：（1）如图①中，即为所求．（2）如图②中，即为所求．（3）即为所求．17．（10分）2020年2月，贵州省积极响应国家“停课不停学”的号召，推出了“空中黔课”．为了解某中学初三学生每天听空中黔课的时间，随机调查了该校部分初三学生．根据调查结果，绘制出了如图统计图表（不完整），请根据相关信息，解答下列问题：部分初三学生每天听空中黔课时间的人数统计表时间1.522.533.54人数人266104（1）本次共调查的学生人数为　50　，在表格中，　　；（2）统计的这组数据中，每天听空中黔课时间的中位数是　　，众数是　　；（3）请就疫情期间如何学习的问题写出一条你的看法． 【解答】解：（1）本次共调查的学生人数为：（人，，故答案为：50，22；（2）由条形统计图得，2个1.5，6个2，6个2.5，10个3，22个3.5，4个4，第25个数和第26个数都是，中位数是；出现了22次，出现的次数最多，众数是，故答案为：，；（3）就疫情期间如何学习的问题，我的看法是：认真听课，独立思考（答案不唯一）．18．（10分）如图，四边形是矩形，是边上一点，点在的延长线上，且．（1）求证：四边形是平行四边形；（2）连接，若，，，求四边形的面积．【解答】（1）证明：四边形是矩形，，，， ，即，，四边形是平行四边形；（2）解：连接，如图，四边形是矩形，，在中，，，，，，，，四边形的面积．19．（10分）如图，一次函数的图象与反比例函数的图象相交，其中一个交点的横坐标是2．（1）求反比例函数的表达式；（2）将一次函数的图象向下平移2个单位，求平移后的图象与反比例函数图象的交点坐标； （3）直接写出一个一次函数，使其过点，且与反比例函数的图象没有公共点．【解答】解：（1）将代入，故其中交点的坐标为，将代入反比例函数表达式并解得：，故反比例函数表达式为：①；（2）一次函数的图象向下平移2个单位得到②，联立①②并解得：，故交点坐标为或；（3）设一次函数的表达式为：③，联立①③并整理得：，两个函数没有公共点，故△，解得：，故可以取（答案不唯一），故一次函数表达式为：（答案不唯一）．20．（10分）“2020 第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动，规则是：准备3张大小一样，背面完全相同的卡片，3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》，将它们背面朝上洗匀后任意抽出一张，抽到卡片后可以免费领取卡片上相应的书籍．（1）在上面的活动中，如果从中随机抽出一张卡片，记下内容后不放回，再随机抽出一张卡片，请用列表或画树状图的方法，求恰好抽到2张卡片都是《辞海》的概率；（2）再添加几张和原来一样的《消防知识手册》卡片，将所有卡片背面朝上洗匀后，任意抽出一张，使得抽到《消防知识手册》卡片的概率为，那么应添加多少张《消防知识手册》卡片？请说明理由．【解答】解：（1）把《消防知识手册》《辞海》《辞海》分别即为、、，画树状图如图：共有6个等可能的结果，恰好抽到2张卡片都是《辞海》的结果有2个，恰好抽到2张卡片都是《辞海》的概率为；（2）设应添加张《消防知识手册》卡片，由题意得：，解得：，经检验，是原方程的解；答：应添加4张《消防知识手册》卡片．21．（8分）脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高所在的直线，为了测量房屋的高度，在地面上点测得屋顶的仰角为，此时地面上点、屋檐上点、屋顶上点三点恰好共线，继续向房屋方向走到达点时，又测得屋檐 点的仰角为，房屋的顶层横梁，，交于点（点，，在同一水平线上）．（参考数据：，，，（1）求屋顶到横梁的距离；（2）求房屋的高（结果精确到．【解答】解：（1）房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高所在的直线，，，，，在中，，，，，（米；答：屋顶到横梁的距离为4.2米；（2）过作于，设，在中，，，，， 在中，，，，，，，解得：，（米，答：房屋的高为14米．22．（10分）第33个国际禁毒日到来之际，贵阳市策划了以“健康人生绿色无毒”为主题的禁毒宣传月活动，某班开展了此项活动的知识竞赛．学习委员为班级购买奖品后与生活委员对话如下：（1）请用方程的知识帮助学习委员计算一下，为什么说学习委员搞错了； （2）学习委员连忙拿出发票，发现的确错了，因为他还买了一本笔记本，但笔记本的单价已模糊不清，只能辨认出单价是小于10元的整数，那么笔记本的单价可能是多少元？【解答】解：（1）设单价为6元的钢笔买了支，则单价为10元的钢笔买了支，根据题意，得：，解得，因为钢笔的数量不可能是小数，所以学习委员搞错了；（2）设笔记本的单价为元，根据题意，得：，整理，得：，因为，随的增大而增大，所以，取整数，，21．当时，；当时，，所以笔记本的单价可能是2元或6元．23．（10分）如图，为的直径，四边形内接于，对角线，交于点，的切线交的延长线于点，切点为，且．（1）求证：；（2）若，，求的值． 【解答】解：（1）证明：，又，，；（2）是的切线，，是的直径，，，，，，，，，，，，， ，，，，，，，，，，，，．24．（12分）2020年体育中考，增设了考生进入考点需进行体温检测的要求．防疫部门为了解学生错峰进入考点进行体温检测的情况，调查了一所学校某天上午考生进入考点的累计人数（人与时间（分钟）的变化情况，数据如下表：（表中表示时间（分钟）0123456789 人数（人0170320450560650720770800810810（1）根据这15分钟内考生进入考点的累计人数与时间的变化规律，利用初中所学函数知识求出与之间的函数关系式；（2）如果考生一进考点就开始测量体温，体温检测点有2个，每个检测点每分钟检测20人，考生排队测量体温，求排队人数最多时有多少人？全部考生都完成体温检测需要多少时间？（3）在（2）的条件下，如果要在12分钟内让全部考生完成体温检测，从一开始就应该至少增加几个检测点？【解答】解：（1）由表格中数据的变化趋势可知，①当时，是的二次函数，当时，，二次函数的关系式可设为：，由题意可得：，解得：，二次函数关系式为：，②当时，，与之间的函数关系式为：；（2）设第分钟时的排队人数为人，由题意可得：， ①当时，，当时，的最大值，②当时，，随的增大而减小，，排队人数最多时是490人，要全部考生都完成体温检测，根据题意得：，解得：，答：排队人数最多时有490人，全部考生都完成体温检测需要20.25分钟；（3）设从一开始就应该增加个检测点，由题意得：，解得，是整数，的最小整数是2，一开始就应该至少增加2个检测点．25．（12分）如图，四边形是正方形，点为对角线的中点．（1）问题解决：如图①，连接，分别取，的中点，，连接，则与的数量关系是　　，位置关系是　　；（2）问题探究：如图②，△是将图①中的绕点按顺时针方向旋转得到的三角形，连接，点，分别为，的中点，连接，．判断的形状，并证明你的结论；（3）拓展延伸：如图③，△是将图①中的绕点按逆时针方向旋转得到的三角形，连接，点，分别为，的中点，连接，．若正方形 的边长为1，求的面积．【解答】解：（1）点为对角线的中点，，，为的中点，为的中点，，，，；故答案为：，．（2）的形状是等腰直角三角形．理由如下：连接并延长交于点， 四边形是正方形，，，将绕点按顺时针方向旋转得到△，△是等腰直角三角形，，，，，又点是的中点，，△，，，，，△为等腰直角三角形．，，也为等腰直角三角形．又点为的中点，，且，的形状是等腰直角三角形；（3）延长交边于点，连接，． 四边形是正方形，是对角线，，由旋转得，四边形是矩形，，，为等腰直角三角形．点是的中点，，，，△，，，，，△为等腰直角三角形，点是的中点，，，，， ，．．