2019九年级数学上册 专题突破讲练 解决圆锥问题的四字秘诀试题 （新版）青岛版 5页

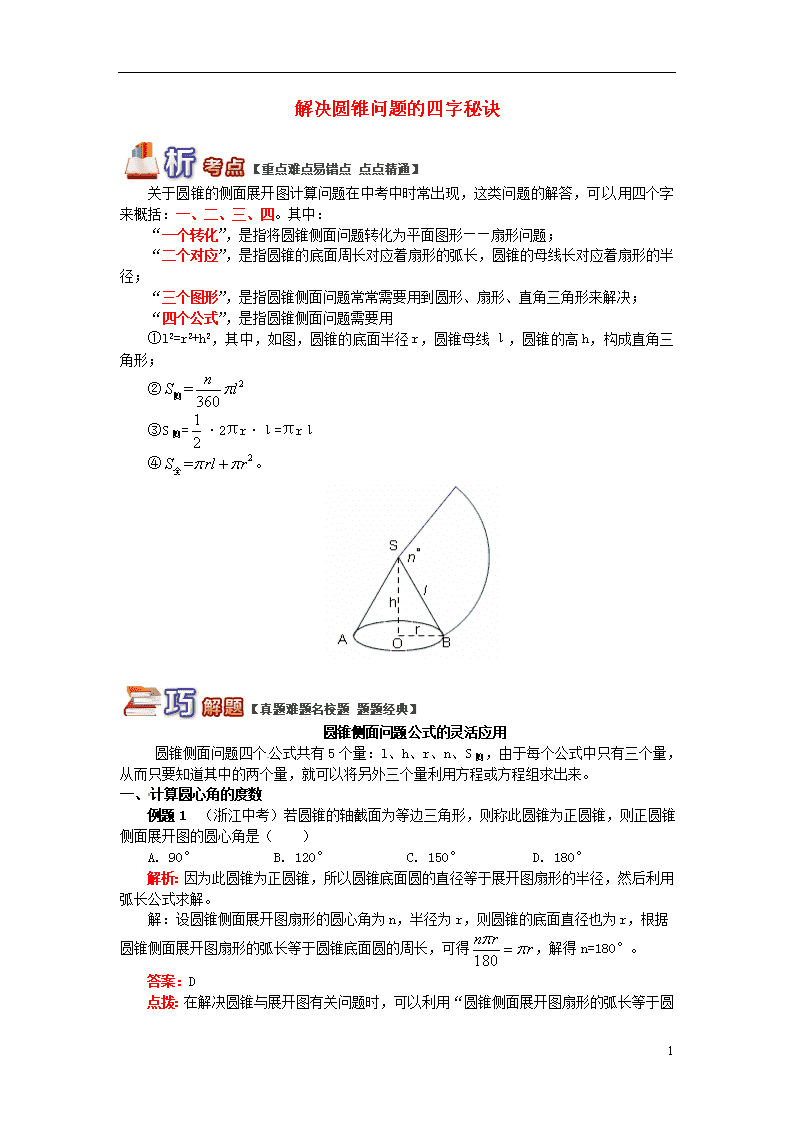
解决圆锥问题的四字秘诀 关于圆锥的侧面展开图计算问题在中考中时常出现，这类问题的解答，可以用四个字来概括：一、二、三、四。其中：‎ ‎“一个转化”，是指将圆锥侧面问题转化为平面图形——扇形问题；‎ ‎“二个对应”，是指圆锥的底面周长对应着扇形的弧长，圆锥的母线长对应着扇形的半径；‎ ‎“三个图形”，是指圆锥侧面问题常常需要用到圆形、扇形、直角三角形来解决；‎ ‎“四个公式”，是指圆锥侧面问题需要用 ‎①l2=r2+h2，其中，如图，圆锥的底面半径r，圆锥母线ι，圆锥的高h，构成直角三角形；‎ ‎②‎ ‎③S侧=·2πr·ι=πrι ‎ ‎④。‎ 圆锥侧面问题公式的灵活应用 圆锥侧面问题四个公式共有5个量：l、h、r、n、S侧，由于每个公式中只有三个量，从而只要知道其中的两个量，就可以将另外三个量利用方程或方程组求出来。‎ 一、计算圆心角的度数 例题1 （浙江中考）若圆锥的轴截面为等边三角形，则称此圆锥为正圆锥，则正圆锥侧面展开图的圆心角是（ ）‎ A. 90° B. 120° C. 150° D. 180°‎ 解析：因为此圆锥为正圆锥，所以圆锥底面圆的直径等于展开图扇形的半径，然后利用弧长公式求解。‎ 解：设圆锥侧面展开图扇形的圆心角为n，半径为r，则圆锥的底面直径也为r，根据圆锥侧面展开图扇形的弧长等于圆锥底面圆的周长，可得，解得n=180°。‎ 答案：D 点拨：在解决圆锥与展开图有关问题时，可以利用“‎ 5‎ 圆锥侧面展开图扇形的弧长等于圆锥底面圆的周长”这一规律解决问题。‎ 二、计算圆锥的底面积 例题2 如图，圆锥形冰淇淋盒的母线长是‎13cm，高是‎12cm，则该圆锥形底面圆的面积是（ ）‎ A. 10πcm2 B. 25πcm‎2 ‎C. 60πcm2 D. 65πcm2‎ 解析：作出圆锥的轴切面图，再根据等腰三角形“三线合一”的性质转化为直角三角形，利用勾股定理求出圆锥底面圆的半径，进而求出其面积。‎ 解：作出圆锥的轴切面图及高，如图，则AB＝‎13cm，AD＝‎12 cm，AD⊥BC，BC＝2BD，所以BD＝‎5 cm，因而底面圆的面积为πr2＝25π（cm2），故选B。‎ 答案：B 点拨：圆锥的轴切面图为等腰三角形，等腰三角形底边上的高为圆锥的高，腰为圆锥的母线长，底边为圆锥底面圆的直径，圆锥轴切面的相关计算通常转化为直角三角形，再利用勾股定理进行计算。‎ 三、计算圆锥的侧面积 例题3 在学校组织的实践活动中，小新同学用纸板制作了一个圆锥模型，它的底面半径为1，高为2，则这个圆锥的侧面积（ ）‎ A. 4π B. 3π C. 2π D. 2π 解析：先根据勾股定理求得圆锥的母线长，再代入圆锥侧面积的公式计算即可。‎ 解：∵圆锥的底面半径为r=1，高为2，∴圆锥的母线长l=，∴圆锥的侧面积==π×1×3=3π，故选B。‎ 答案：B 点拨：这类题要熟记圆锥的侧面积公式S=πrl及圆锥的高h、母线l、底面半径为r的关系：。解决这类问题的方法有：①列式计算，②运用方程思想列方程来计算。‎ 5‎ 计算线路最短问题 满分训练 如图，圆锥的母线长是3，底面半径是1，A是底面圆周上一点，一只小虫从点A出发，绕侧面爬行一周，再回到点A的最短的路线长是多少？ ‎ 解析：我们知道“两点之间，线段最短”，沿母线SA作侧面展开图如图，本题实际是求将圆锥的侧面沿着母线OA展开，求点A到A′的距离AA′。‎ 解：将圆锥沿母线SA作侧面展开图，得扇形O AA′，‎ 设扇形的圆心角为θ，因为圆锥的底面半径为r=1，母线长为3，根据2πr=，得 ‎2π×1=，所以θ=120°。即扇形的圆心角∠AOA′为120°，作OD⊥AA′，垂足为D，在Rt△AOD中，∠OAD=30°，OA=3。 所以OD=，据勾股定理，得可求得AD=，所以AA′=2AD=。‎ 答案：‎ 点拨：小虫从点A出发，绕圆锥侧面爬行，从圆锥上看是曲线，而在侧面展开图上看是直线，“化曲为直”是解决此类问题的关键。‎ ‎（答题时间：30分钟）‎ ‎1. 用半径为‎3cm，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为（ ）‎ A. 2πcm B. ‎1.5cm C. πcm D. ‎‎1cm ‎2. 已知圆锥的底面半径为‎6cm，高为‎8cm，则这个圆锥的母线长为（ ）。‎ A. ‎12cm B. ‎10cm C. ‎8cm D. ‎‎6cm 5‎ ‎3. 圆锥底面圆的半径为‎3cm，其侧面展开图是半圆，则圆锥母线长为（ ）‎ A. ‎3cm　 　 B. ‎6cm　　 　 C. ‎9cm　 　　 D. ‎12cm ‎ ‎4. 若圆锥的侧面展开图为半圆，则该圆锥的母线l与底面半径r的关系是（ ）‎ A. l＝2r B. l＝3r C. l＝r D. l＝‎ ‎*5. 一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图扇形的圆心角是 °。‎ ‎6. 圆锥的侧面积为‎6‎cm2，底面圆的半径为‎2cm，则这个圆锥的母线长为 cm ‎*7. 已知一个扇形的半径为60厘米，圆心角为150°。用它围成一个圆锥的侧面，那么圆锥的底面半径为厘米。‎ ‎*8. 若圆锥的母线长为‎5cm，底面圆的半径为‎3cm，则它的侧面展开图的面积为 cm2（结果保留π）。‎ ‎*9. 用半径为‎10cm，圆心角为216°的扇形作一个圆锥的侧面，求这个圆锥的高。‎ ‎**10. 如图所示的一扇形纸片，圆心角∠AOB为120°，弦AB的长为，用它围成一个圆锥的侧面（接缝忽略不计），求该圆锥底面的半径。‎ ‎*11. 已知圆锥的底面周长是10π，其侧面展开后所得扇形的圆心角为90°，求该圆锥的母线长。‎ ‎**12. 如图，圆锥的侧面展开图是一个半圆，求母线AB与高AO的夹角。‎ 5‎ ‎ ‎ ‎1. D 解析：依题意，得这个圆锥的底面半径＝÷2π＝1，故选D。‎ ‎2. B 解析：先根据半径与高互相垂直，然后利用勾股定理求母线长。∵ r2＋h2＝l2，∴ 62＋82＝l2，∴ l＝10㎝，故选B。‎ ‎3. B 解析：圆锥的母线长=圆锥的底面周长×=2×π×3×=‎6cm。故选B。‎ ‎4. A 解析：根据以上分析，则圆锥的底面周长为，展开图扇形弧长是，因此，则 l＝2r，故选A。‎ ‎*5. 180° 解析：设圆锥的母线长为l，底面半径为r， 圆心角n，则，即，∴侧面展开图扇形的圆心角为n=360°×=180°。故答案为180°。‎ ‎6. 3 解析：设圆锥的母线长为R，因底面圆的半径为‎2cm，所以底面圆的周长=侧面扇形的弧长=2×2=4，又扇形的面积=×4×R=6，解得R=3，故填3。‎ ‎*7. 25 解析：设圆锥的底面半径为r，则圆锥的母线长R=‎60 cm，因为圆锥的底面周长等于其侧面展开图的弧长，所以2πr=，解得r=25。‎ ‎*8. 15π 解析：∵圆锥的侧面积S=πrl，，r=‎3 ‎cm，l=5∴S=15π cm2。‎ ‎*9. 解析：扇形的弧长是：=12π（cm），设圆锥的底面半径是r，则2πr=12π，解得：r=‎6cm，则圆锥的高是：=8（cm）。‎ ‎**10. 解析：过O点作OE⊥AB，垂足为点E，∵OA=OB，AB=cm，∴AE=cm，∠AOE=60º，∴OA=‎2cm，∴弧AB的长，设该圆锥底面的半径为r，∴，∴r=cm。‎ ‎*11. 解析：设圆锥的母线长为l。∵圆锥的底面周长是10π，∴圆锥侧面展开图（扇形）的弧长是10π。∵侧面展开后所得扇形的圆心角为90°，∴。∴l＝20，即该圆锥的母线长是20。‎ ‎**12. 解析：因为2r=l。 所以l=2r，所以sin∠BAO=，所以∠BAO=30°，所以母线AB与高AO的夹角为30°。‎ 5‎