湖北省黄冈市中考数学试卷（含解析） 27页

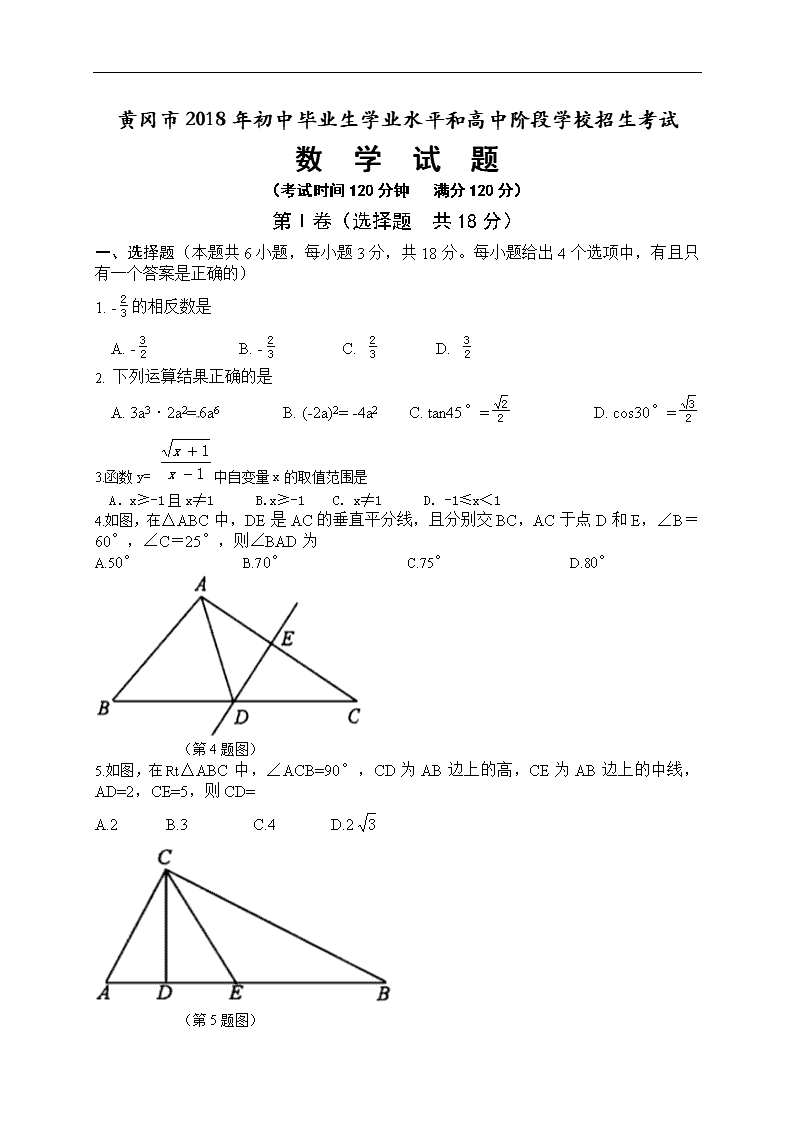
黄冈市2018年初中毕业生学业水平和高中阶段学校招生考试 数 学 试 题 ‎（考试时间120分钟 满分120分）‎ 第Ⅰ卷（选择题 共18分）‎ 一、选择题（本题共6小题，每小题3分，共18分。每小题给出4个选项中，有且只有一个答案是正确的）‎ ‎1. -的相反数是 ‎ A. - B. - C. D. ‎ ‎2. 下列运算结果正确的是 ‎ A. 3a3·2a2=6a6 B. (-2a)2= -4a2 C. tan45°= D. cos30°=‎ ‎3.函数y= 中自变量x的取值范围是 A．x≥-1且x≠1 B.x≥-1 C. x≠1 D. -1≤x＜1‎ ‎4.如图，在△ABC中，DE是AC的垂直平分线，且分别交BC，AC于点D和E，∠B＝60°，∠C＝25°，则∠BAD为 A.50° B.70° C.75° D.80°‎ ‎（第4题图）‎ ‎5.如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，CE为AB边上的中线，AD=2，CE=5，则CD=‎ A.2 B.3 C.4 D.2‎ ‎（第5题图）‎ ‎6.当a≤x≤a+1时，函数y=x2-2x+1的最小值为1，则a的值为 A.-1 B.2 C.0或2 D.-1或2‎ 第Ⅱ卷（非选择题 共102分）‎ 二、填空题（本题共8小题，每小题3分，共24分）‎ ‎7.实数16 800 000用科学计数法表示为______________________.‎ ‎8.因式分解：x3-9x=___________________________.‎ ‎9.化简(-1)0+()-2-+=________________________.‎ ‎10.若a-=，则a2+值为_______________________.‎ ‎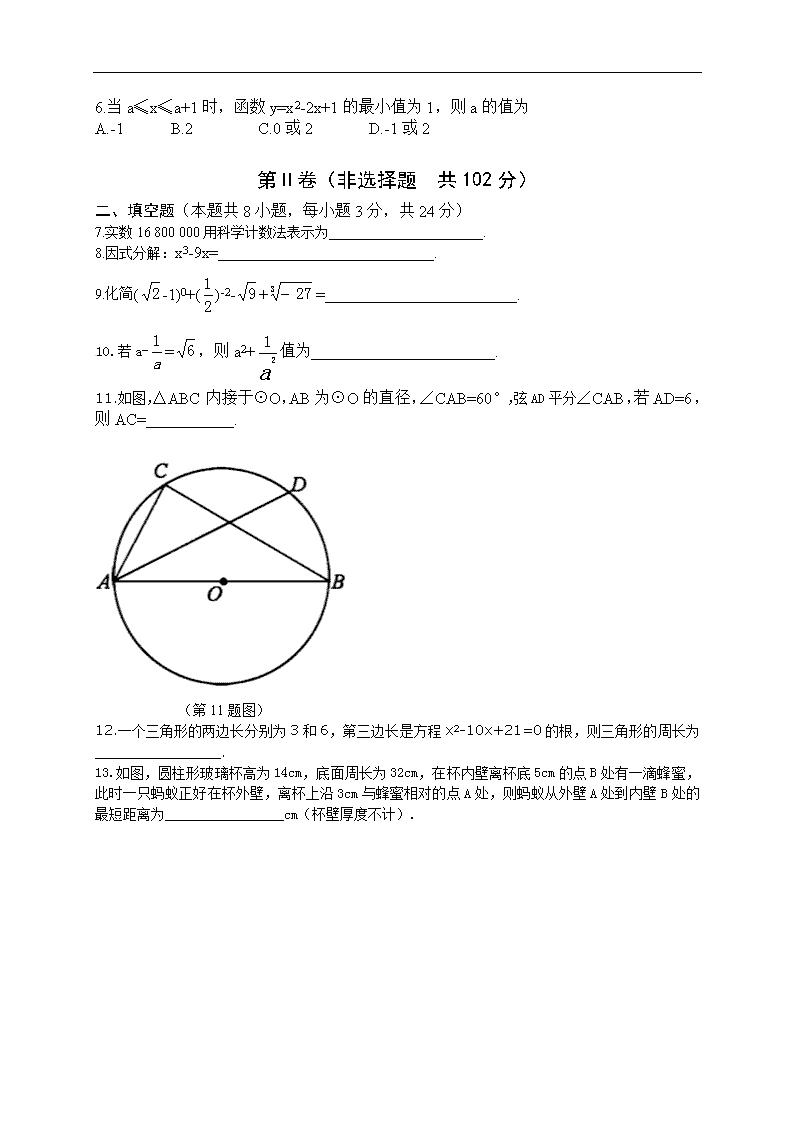11.如图，△ABC内接于⊙O，AB为⊙O的直径，∠CAB=60°，弦AD平分∠CAB，若AD=6，则AC=___________.‎ ‎（第11题图）‎ ‎12.一个三角形的两边长分别为3和6，第三边长是方程x2-10x+21=0的根，则三角形的周长为______________.‎ ‎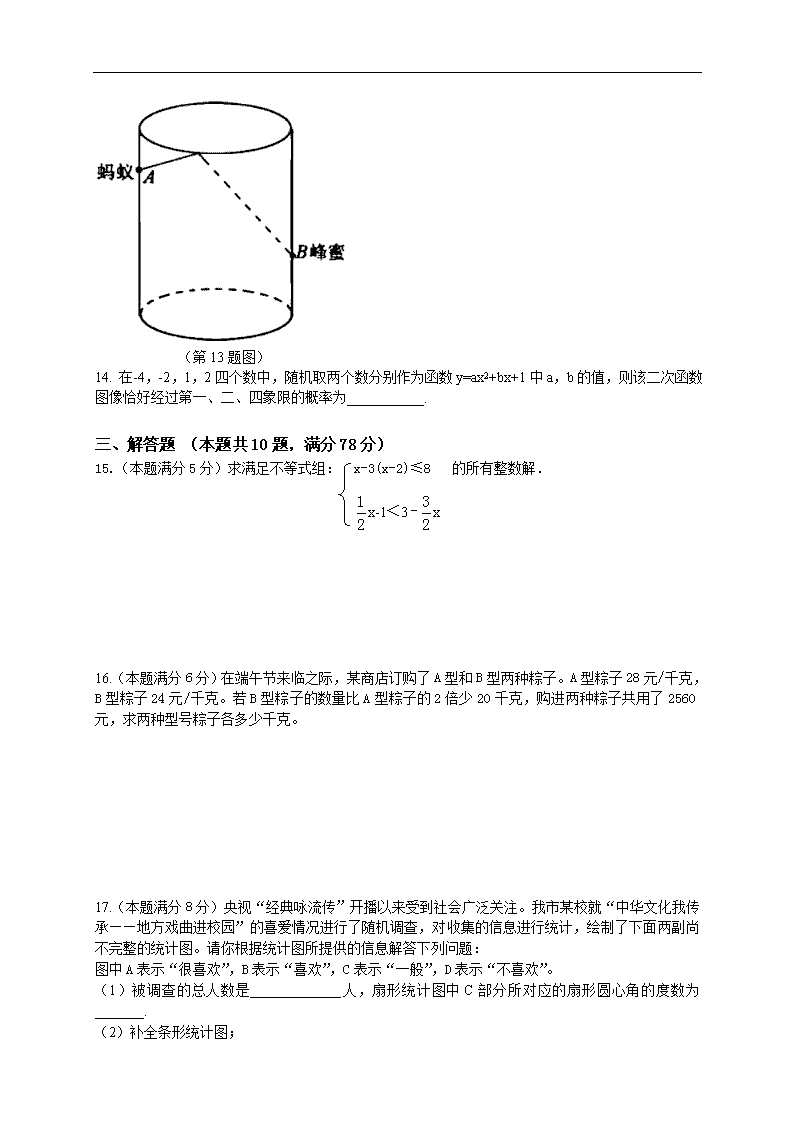13.如图，圆柱形玻璃杯高为14cm，底面周长为32cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为_________________cm（杯壁厚度不计）.‎ ‎（第13题图）‎ ‎14. 在-4，-2，1，2四个数中，随机取两个数分别作为函数y=ax2+bx+1中a，b的值，则该二次函数图像恰好经过第一、二、四象限的概率为___________.‎ 三、解答题 （本题共10题，满分78分） ‎ ‎15.（本题满分5分）求满足不等式组： x-3(x-2)≤8 的所有整数解．‎ ‎ x-1＜3 -x ‎16.（本题满分6分）在端午节来临之际，某商店订购了A型和B型两种粽子。A型粽子28元/千克，B型粽子24元/千克。若B型粽子的数量比A型粽子的2倍少20千克，购进两种粽子共用了2560元，求两种型号粽子各多少千克。‎ ‎17.（本题满分8分）央视“经典咏流传”开播以来受到社会广泛关注。我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查，对收集的信息进行统计，绘制了下面两副尚不完整的统计图。请你根据统计图所提供的信息解答下列问题：‎ 图中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”。‎ ‎（1）被调查的总人数是_____________人，扇形统计图中C部分所对应的扇形圆心角的度数为_______.‎ ‎（2）补全条形统计图；‎ ‎（3）若该校共有学生1800人，请根据上述调查结果，估计该校学生中A类有__________人； ‎ ‎（4）在抽取的A类5人中，刚好有3个女生2个男生，从中随机抽取两个同学担任两角色，用树形图或列表法求出被抽到的两个学生性别相同的概率。‎ ‎18.（本题满分7分）如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C.‎ ‎（1）求证：∠CBP=∠ADB.‎ ‎（2）若OA=2，AB=1，求线段BP的长.‎ ‎（第18题图）‎ ‎19.（本题满分6分）如图，反比例函数y=（x＞0）过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线BC交反比例函数图象于点B.‎ ‎（1）求k的值与B点的坐标；‎ ‎（2）在平面内有点D，使得以A，B，C，D四点为顶点的四边形为平行四边形，试写出符合条件的所有D点的坐标.‎ ‎20.（本题满分8分）如图，在口ABCD中，分别以边BC，CD作等腰△BCF，△CDE，使BC=BF，CD=DE，∠CBF＝∠CDE，连接AF，AE.‎ ‎（1）求证：△ABF≌△EDA；‎ ‎（2）延长AB与CF相交于G，若AF⊥AE，求证BF⊥BC.‎ ‎（第20题图）‎ ‎21.（本题满分7分）如图，在大楼AB正前方有一斜坡CD，坡角∠DCE=30°，楼高AB=60米，在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的D处测得楼顶B的仰角为45°，其中点A,C,E在同一直线上.‎ ‎（1）求坡底C点到大楼距离AC的值；‎ ‎（2）求斜坡CD的长度.‎ ‎（第21题图）‎ ‎22.（本题满分8分）已知直线l:y=kx+1与抛物线y=x2-4x ‎（1）求证：直线l与该抛物线总有两个交点；‎ ‎（2）设直线l与该抛物线两交点为A，B，O为原点，当k=-2时，求△OAB的面积.‎ ‎23.（本题满分9分）我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：y= x+4（1≤x≤8，x为整数）‎ ‎ -x+20（9≤x≤12，x为整数），每件产品的利润z（元）与月份x（月）的关系如下表：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ z ‎19‎ ‎18‎ ‎17‎ ‎16‎ ‎15‎ ‎14‎ ‎13‎ ‎12‎ ‎11‎ ‎10‎ ‎10‎ ‎10‎ ‎（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；‎ ‎（2）若月利润w（万元）=当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；‎ ‎（3）当x为何值时，月利润w有最大值，最大值为多少？‎ ‎24.（本题满分14分）如图，在直角坐标系XOY中，菱形OABC的边OA在x轴正半轴上，点B，C在第一象限，∠C=120°，边长OA=8，点M从原点O出发沿x轴正半轴以每秒1个单位长的速度作匀速运动，点N从A出发沿边AB—BC—CO以每秒2个单位长的速度作匀速运动。过点M作直线MP垂直于x轴并交折线OCB于P，交对角线OB于Q，点M和点N同时出发，分别沿各自路线运动，点N运动到原点O时，M和N两点同时停止运动。‎ ‎（1）当t=2时，求线段PQ的长；‎ ‎（2）求t为何值时，点P与N重合；‎ ‎（3）设△APN的面积为S，求S与t的函数关系式及t的取值范围. ‎ 黄冈市2018年初中毕业生学业水平和高中阶段学校招生考试 数 学 试 题 ‎（考试时间120分钟 满分120分）‎ 第Ⅰ卷（选择题 共18分）‎ 一、选择题（本题共6小题，每小题3分，共18分。每小题给出4个选项中，有且只有一个答案是正确的）‎ ‎1. -的相反数是 ‎ A. - B. - C. D. ‎ ‎【考点】相反数．‎ ‎【分析】只有符号不同的两个数，我们就说其中一个是另一个的相反数；0的相反数是0。一般地，任意的一个有理数a，它的相反数是-a。a本身既可以是正数，也可以是负数，还可以是零。本题根据相反数的定义，可得答案．‎ ‎【解答】解：因为与-是符号不同的两个数 ‎ 所以-的相反数是.‎ 故选C.‎ ‎【点评】本题考查了绝对值的性质，如果用字母a表示有理数，则数a 绝对值要由字母a本身的取值来确定：‎ ‎①当a是正有理数时，a的绝对值是它本身a；‎ ‎②当a是负有理数时，a的绝对值是它的相反数-a；‎ ‎③当a是零时，a的绝对值是零．‎ ‎2. 下列运算结果正确的是 ‎ A. 3a3·2a2=6a6 B. (-2a)2= -4a2 C. tan45°= D. cos30°=‎ ‎【考点】同底数幂的乘法与除法、幂的乘方，以及特殊角的三角函数值。‎ ‎【分析】根据同底数幂的乘法、幂的乘方的运算法则以及特殊角的三角函数值计算即可．‎ ‎【解答】解：A. 根据同底数幂的乘法，3a3·2a2=6a5，故本选项错误；‎ B. 根据幂的乘方，(-2a)2= 4a2，故本选项错误 C．根据特殊角的三角函数值，tan45°=1，故本选项错误；‎ D．根据特殊角的三角函数值，cos30°=，故本选项正确．‎ 故选D．‎ ‎【点评】本题考查了同底数幂的乘法与除法、幂的乘方，以及特殊角的三角函数值，熟知运算法则、熟记特殊角的三角函数值是钥匙的关键。‎ ‎3.函数y= 中自变量x的取值范围是 A．x≥-1且x≠1 B.x≥-1 C. x≠1 D. -1≤x＜1‎ ‎【考点】函数自变量的取值范围。‎ ‎【分析】自变量x的取值范围必须使函数有意义，中x+1≥0；分式作为除式，则x-1≠0.综上即可得解。‎ ‎【解答】解：依题意，得 x+1≥0‎ x-1≠0‎ ‎∴x≥-1且x≠1.‎ 故选A.‎ ‎【点评】本题考查了函数自变量的取值范围。要使二次根式有意义，必须使被开方数为非负数；分式的分母不能为零。‎ ‎4.如图，在△ABC中，DE是AC的垂直平分线，且分别交BC，AC于点D和E，∠B＝60°，∠C＝25°，则∠BAD为 A.50° B.70° C.75° D.80°‎ ‎（第4题图）‎ ‎【考点】垂直平分线的性质，三角形的内角和定理。‎ ‎【分析】由三角形的内角和定理，得∠BAC的度数，又由垂直平分线的性质，知∠C＝∠DAC=25°，从而得出∠BAD的度数。‎ ‎【解答】解：由三角形的内角和定理，得∠BAC=180°-∠B-∠C=180°-60°-25°=95°。‎ 又由垂直平分线的性质，知∠C＝∠DAC=25°，‎ ‎∴∠BAC=∠BAD+∠DAC=∠BAD+∠C=∠BAD+25°=9‎ ‎∴∠BAD=95°-25°=70°.‎ 故选B.‎ ‎【点评】本题考查了垂直平分线的性质，三角形的内角和定理。熟练掌握性质和定理是解题的关键。‎ ‎5.如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，CE为AB边上的中线，AD=2，CE=5，则CD=‎ A.2 B.3 C.4 D.2‎ ‎（第5题图）‎ ‎【考点】直角三角形斜边上的中线的性质，勾股定理。‎ ‎【分析】由直角三角形斜边上的中线等于斜边的一半，可得CE=AE=5，又知AD=2，可得DE=AE-AD=5-2=3，在Rt△CDE中，运用勾股定理可得直角边CD的长。‎ ‎【解答】解：在Rt△ABC中，∠ACB=90°，CE为AB边上的中线，‎ ‎∴CE=AE=5，‎ 又∵AD=2，‎ ‎∴DE=AE-AD=5-2=3，‎ ‎∵CD为AB边上的高 ‎∴∠CDE=90°，‎ ‎∴△CDE 为Rt△‎ ‎∴CD===4‎ 故选C.‎ ‎【点评】本题考查了直角三角形斜边上的中线的性质，勾股定理。得出DE的长是解题的关键。‎ ‎6.当a≤x≤a+1时，函数y=x2-2x+1的最小值为1，则a的值为 A.-1 B.2 C.0或2 D.-1或2‎ ‎【考点】不等式组，二次函数的最值。‎ ‎【分析】由题意知函数y=x2-2x+1≥1，可得出x的取值范围，再由a≤x≤a+1可得出a的值。‎ ‎【解答】解：∵当a≤x≤a+1时，函数y=x2-2x+1的最小值为1，‎ ‎∴y=x2-2x+1≥1，即x2-2x≥0，‎ ‎∴x≥2或x≤0，‎ 当x≥2时，由a≤x，可得a=2,‎ 当x≤0时，由x≤a+1，可得a+1=0,即a=-1‎ 综上，a的值为2或-1，‎ 故选D.‎ ‎【点评】本题考查了不等式组. 弄清题意，解不等式组是关键。‎ 第Ⅱ卷（非选择题 共102分）‎ 二、填空题（本题共8小题，每小题3分，共24分）‎ ‎7.实数16 800 000用科学计数法表示为______________________.‎ ‎【考点】用科学记数法表示较大的数。‎ ‎【分析】确定a×10n（1≤|a|＜10，n为整数）中n的值是易错点，由于16 800 000有8‎ 位，所以可以确定n=8-1=7．‎ ‎【解答】解：16 800 000=1.68×107．‎ 故答案为：1.68×107．‎ ‎【点评】本题考查了科学记数法。把一个数M记成a×10n（1≤|a|＜10，n为整数）的形式，这种记数的方法叫做科学记数法．规律：（1）当|a|≥1时，n的值为a的整数位数减1；（2）当|a|＜1时，n的值是第一个不是0的数字前0的个数，包括整数位上的0．‎ ‎8.因式分解：x3-9x=___________________________.‎ ‎【考点】因式分解。‎ ‎【分析】先提取公因式x，再对余下的多项式利用平方差公式继续分解．‎ ‎【解答】解：x3-9x=x（x2-9），‎ ‎=x（x+3）（x-3）．‎ 故答案为：x（x+3）（x-3）．‎ ‎【点评】本题考查了因式分解-提取公因式法和公式法的综合运用．‎ ‎9.化简(-1)0+()-2-+=________________________.‎ ‎【考点】实数的运算。‎ ‎【分析】根据零次幂、副整数指数幂的运算法则，以及平方根，立方根计算即可。‎ ‎【解答】解：(-1)0+()-2-+=1+22-3-3= -1.‎ 故答案为：-1．‎ ‎【点评】本题考查了实数的运算。掌握零次幂、副整数指数幂、平方根、立方根的运算法则是关键。‎ ‎10.若a-=，则a2+值为_______________________.‎ ‎【考点】完全平方公式.‎ ‎【分析】根据完全平方公式，对已知的算式和各选项分别整理，即可得出答案．‎ ‎【解答】解：∵a-=，‎ ‎∴（a-）2=6，‎ a2+-2=6，‎ ‎∴a2+=8，‎ 故答案为：8．‎ ‎【点评】本题考查了完全平方公式。熟记公式的几个变形公式对解题大有帮助。‎ ‎11.如图，△ABC内接于⊙O，AB为⊙O的直径，∠CAB=60°，弦AD平分∠CAB，若AD=6，则AC=___________.‎ ‎（第11题图）‎ ‎【考点】圆，角平分线，30°角所对的直角边等于的一半，勾股定理.‎ ‎【分析】连结BD，根据30°角所对的直角边等于的一半，易得出BD=AC=AB；再通过勾股定理可求得AB的长，从而得出AC的长。‎ ‎【解答】解：连结BD，‎ ‎∵AB为⊙O的直径，∠CAB=60°，弦AD平分∠CAB，‎ ‎∴∠ABC=∠DAB=30°‎ ‎∴在Rt△ABC和 Rt△ABD中，BD=AC=AB 在Rt△ABD中，AB2=BD2+AD2，即AB2=（AB）2+62，‎ ‎∴AB=4，‎ ‎∴AC=2.‎ 故答案为：2.‎ ‎【点评】本题考查了圆，角平分线，30°角所对的直角边等于的一半，勾股定理. 熟练掌握定理是解题的关键。‎ ‎12.一个三角形的两边长分别为3和6，第三边长是方程x2-10x+21=0的根，则三角形的周长为______________.‎ ‎【考点】解一元二次方程，三角形三边的关系.‎ ‎【分析】将已知的方程x2-10x+21=0左边分解因式，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程，求出一次方程的解得到原方程的解为3或7，利用三角形的两边之和大于第三边进行判断，得到满足题意的第三边的长，从而求得三角形的周长．‎ ‎【解答】解：x2-10x+21=0，‎ 因式分解得：（x-3）（x-7）=0，‎ 解得：x1=3，x2=7，‎ ‎∵三角形的第三边是x2-10x+21=0的根，‎ ‎∴三角形的第三边为3或7，‎ 当三角形第三边为3时，3+3=6，不能构成三角形，舍去；‎ 当三角形第三边为7时，三角形三边分别为3，6，7，能构成三角形，‎ 则第三边的长为7．‎ ‎∴三角形的周长为: 3+6+7=16.‎ 故答案为：16.‎ ‎【点评】本题考查了利用因式分解法求解解一元二次方程，以及三角形三边的关系. 利用因式分解法求解解一元二次方程时，首先将方程右边化为0，左边分解因式，然后利用两数相乘积为0，两因式中至少有一个为0，转化为两个一元一次方程来求解。‎ ‎13.如图，圆柱形玻璃杯高为14cm，底面周长为32cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为_________________cm（杯壁厚度不计）.‎ ‎（第13题图）‎ ‎【考点】平面展开-最短路径问题．‎ ‎【分析】将圆柱体侧面展开，过B作BQ⊥EF于Q，作A关于EH的对称点A′，连接A′B交EH于P，连接AP，则AP+PB就是蚂蚁到达蜂蜜的最短距离，求出A′Q，BQ，根据勾股定理求出A′B即可．‎ ‎【解答】解：沿过A的圆柱的高剪开，得出矩形EFGH，过B作BQ⊥EF于Q，作A关于EH的对称点A′，连接A′B交EH于P，连接AP，则AP+PB就是蚂蚁到达蜂蜜的最短距离，‎ ‎ ‎ ‎ ‎ ‎∵AE=A′E，A′P=AP，‎ ‎∴AP+PB=A′P+PB=A′B，‎ ‎∵BQ=×32cm=16cm，A′Q=14cm-5cm+3cm=12cm，‎ 在Rt△A′QB中，由勾股定理得：A′B==20cm.‎ 故答案为：20.‎ ‎【点评】本题考查了平面展开-最短路径问题．将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力． ‎ ‎ ‎ ‎14. 在-4，-2，1，2四个数中，随机取两个数分别作为函数y=ax2+bx+1中a，b的值，则该二次函数图像恰好经过第一、二、四象限的概率为___________.‎ ‎【考点】概率．‎ ‎【分析】首先利用列表法求得所有点的情况，再由二次函数图像恰好经过第一、二、四象限，即可求得答案．‎ ‎【解答】解：列表得：‎ ‎ a b ‎-4‎ ‎-2‎ ‎1‎ ‎2‎ ‎-4‎ ‎（-2，-4）‎ ‎（1，-4）‎ ‎（2，-4）‎ ‎-2‎ ‎（-4，-2）‎ ‎（1，-2）‎ ‎（2，-2）‎ ‎1‎ ‎（-4，1）‎ ‎（-2，1）‎ ‎（2，1）‎ ‎2‎ ‎（-4，2）‎ ‎（-2，2）‎ ‎（1，2）‎ ‎∴一共有12种情况，‎ ‎∵若二次函数图像恰好经过第一、二、四象限，则△=b2-4ac＞0，且a＞0，‎ ‎∴符合要求的点有（1，-4）,（2，-4）2个 ‎∴所有的二次函数图像恰好经过第一、二、四象限的概率为=.‎ 本题考查了概率．当试验中存在两个元素且出现的所有可能的结果较多时，我们常用列表的方式，列出所有可能的结果，再求出概率．‎ 三、解答题 （本题共10题，满分78分） ‎ ‎15.（本题满分5分）求满足不等式组： x-3(x-2)≤8 的所有整数解．‎ ‎ x-1＜3 -x ‎【考点】解不等式组.‎ ‎【分析】先求出不等式组的解集，再求出不等式组的整数解即可．‎ ‎【解答】解：由x-3(x-2)≤8得：x≥1； ‎ ‎ 由x-1＜3 -x得：x＜2；‎ ‎ ∴不等式组的解为：-1≤x＜2‎ ‎ 所有整数解为：-1，0，1.‎ ‎【点评】本题考查了解一元一次不等式组，求不等式组的整数解的应用，解此题的关键是求出不等式组的解集，难度适中．‎ ‎16.（本题满分6分）在端午节来临之际，某商店订购了A型和B型两种粽子。A型粽子28元/千克，B型粽子24元/千克。若B型粽子的数量比A型粽子的2倍少20千克，购进两种粽子共用了2560元，求两种型号粽子各多少千克。‎ ‎【考点】二元一次方程组的应用.‎ ‎【分析】设A型粽子x千克，B型粽子y千克，根据B型粽子的数量比A型粽子的2倍少20千克，购进两种粽子共用了2560元，可列出方程组．‎ ‎【解答】解：设A型粽子x千克，B型粽子y千克，由题意得：‎ ‎ y=2x-20‎ ‎ 28x+24y=2560‎ ‎ 解得： x=40‎ ‎ y=60，并符合题意。‎ ‎ ∴A型粽子40千克，B型粽子60千克.‎ 答：A型粽子40千克，B型粽子60千克.‎ ‎【点评】本题考查了由实际问题抽象出二元一次方程组，难度一般，关键是读懂题意设出未知数找出等量关系．‎ ‎17.（本题满分8分）央视“经典咏流传”开播以来受到社会广泛关注。我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查，对收集的信息进行统计，绘制了下面两副尚不完整的统计图。请你根据统计图所提供的信息解答下列问题：‎ 图中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”。‎ ‎（1）被调查的总人数是_____________人，扇形统计图中C部分所对应的扇形圆心角的度数为_______.‎ ‎（2）补全条形统计图；‎ ‎（3）若该校共有学生1800人，请根据上述调查结果，估计该校学生中A类有__________人； ‎ ‎（4）在抽取的A类5人中，刚好有3个女生2个男生，从中随机抽取两个同学担任两角色，用树形图或列表法求出被抽到的两个学生性别相同的概率。‎ ‎【考点】统计，列表法与树状图法求概率.‎ ‎【分析】（1）根据参加调查的人中，“很喜欢”的占10%，人数是5人，据此即可求；‎ C有30人，是A的6倍，可知“一般”的占60%，利用360°乘以对应的比例即可求.‎ ‎（2）B的人数为：50-5-30-5=10（人），补充在图中即可。‎ ‎（3）将该校共有学生1800人，乘以10%，就可得出该校学生中A类的人数；‎ ‎（4）用列表法与树状图法可求。‎ ‎【解答】解：（1）被调查的总人数是：5÷10%=50（人）.‎ C部分所对应的扇形圆心角的度数为: 360×=216°.‎ ‎（2）如图。‎ ‎（3）1800×10%=180（人）； ‎ ‎（4）‎ 由树形图可得出：共有20种情况，两个学生性别相同的情况数有8种，‎ ‎ 开始 ‎ 女 女 女 男 男 女 女 男 男女 女 男 男 女 女 男 男 女 女 女 男 女 女 女 男 所以两个学生性别相同的概率为=.‎ 答案为：（1）50；216°；（2）如图；（3）180；（4）如上图，（或0.4或40%）（注：过程分析2分，正确结果2分）‎ ‎【点评】本题考查了利用统计图获取信息的能力，涉及用样本估计总体、扇形统计图、列表法与树状图法等。利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题。‎ ‎18.（本题满分7分）如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C.‎ ‎（1）求证：∠CBP=∠ADB.‎ ‎（2）若OA=2，AB=1，求线段BP的长.‎ ‎（第18题图）‎ ‎【考点】圆，切线的性质，相似三角形.‎ ‎【分析】（1）连接OB，证明∠OBD=∠CBP，又OD=OB，∠OBD=∠ODB，∴∠ODB=∠CBP，即∠ADB=∠CBP.‎ ‎（2）证明Rt△ADB∽Rt△APO，即可求得线段BP的长.‎ ‎【解答】证：（1）连接OB，则OB⊥BC，∠OBD＋∠DBC＝90°，‎ ‎ 又AD为直径，∠DBP=∠DBC+∠CBP＝90°，‎ ‎ ∴∠OBD=∠CBP 又OD=OB，∠OBD=∠ODB，‎ ‎∴∠ODB=∠CBP，即∠ADB=∠CBP.‎ 解：（2）在Rt△ADB与Rt△APO中，∠DAB＝∠PAO，‎ ‎ Rt△ADB∽Rt△APO ‎ AB=1，AO=2，AD=4，=，‎ ‎ AP=8，‎ ‎∴BP=AP-AB=8-1=7.‎ ‎【点评】本题考查了圆，直径所对的圆周角是直角，切线的性质，相似三角形的判定和性质. （1）连接OB是解决问题的关键；（2）证明Rt△ADB∽Rt△APO是解决问题的关键。‎ ‎19.（本题满分6分）如图，反比例函数y=（x＞0）过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线BC交反比例函数图象于点B.‎ ‎（1）求k的值与B点的坐标；‎ ‎（2）在平面内有点D，使得以A，B，C，D四点为顶点的四边形为平行四边形，试写出符合条件的所有D点的坐标.‎ ‎【考点】反比例函数数形结合类综合题.‎ ‎【分析】（1）已知反比例函数y=（x＞0）过点A（3，4），将A（3，4）代入到解析式y=即可求得k的值；将C（6，0）的横坐标代入到反比例函数y=中，可得B点的坐标；‎ ‎（2）画出图形即可得出符合条件的所有D点的坐标。‎ ‎【解答】解：（1）代入A（3，4）到解析式y=得k=12，‎ 则反比例函数的解析式为y=，‎ 将C（6，0）的横坐标代入到反比例函数y=中，得y=2‎ ‎∴B点的坐标为：B（6，2）‎ ‎（2）如图，符合条件的所有D点的坐标为：D1（3，2）或D2（3，6）或D3（9，-2）‎ 答案为：D1（3，2）或D2（3，6）或D3（9，-2）‎ ‎【点评】本题考查了反比例函数、平行四边形，是数形结合类综合题. 利用图象解决问题，从图上获取有用的信息，是解题的关键所在．已知点在图象上，那么点一定满足这个函数解析式，反过来如果这点满足函数的解析式，那么这个点也一定在函数图象上．将数形结合在一起，是分析解决问题的一种好方法．‎ ‎20.（本题满分8分）如图，在口ABCD中，分别以边BC，CD作等腰△BCF，△CDE，使BC=BF，CD=DE，∠CBF＝∠CDE，连接AF，AE.‎ ‎（1）求证：△ABF≌△EDA；‎ ‎（2）延长AB与CF相交于G，若AF⊥AE，求证BF⊥BC.‎ ‎（第20题图）‎ ‎【考点】平行四边形、全等三角形，等腰三角形.‎ ‎【分析】（1）先证明∠ABF＝∠ADE，再利用SAS证明△ABF≌△EDA；‎ ‎（2）要证BF⊥BC，须证∠FBC＝90°，通过AF⊥AE挖掘角的量的关系。‎ ‎【解答】（1）证：∵口ABCD， ‎ ‎∴AB=CD=DE，BF=BC=AD ‎ 又∠ABC＝∠ADC，∠CBF＝∠CDE，‎ ‎∴∠ABF＝∠ADE；‎ 在△ABF与△EDA中，‎ ‎　　AB＝DE ‎　　∠ABF＝∠ADE ‎　　BF=AD ‎∴△ABF≌△EDA.‎ ‎（2）由（1）知∠EAD＝∠AFB，∠GBF＝∠AFB+∠BAF，‎ 由口ABCD可得：AD∥BC，‎ ‎∴∠DAG＝∠CBG，‎ ‎∴∠FBC＝∠FBG+∠CBG＝∠EAD+∠FAB+∠DAG=∠EAF=90°，‎ ‎∴BF⊥BC.‎ ‎【点评】本题考查了平行四边形的判定和性质、全等三角形的判定和性质、等腰三角形的性质. 难度一般。‎ ‎21.（本题满分7分）如图，在大楼AB正前方有一斜坡CD，坡角∠DCE=30°，楼高AB=60米，在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的D处测得楼顶B的仰角为45°，其中点A,C,E在同一直线上.‎ ‎（1）求坡底C点到大楼距离AC的值；‎ ‎（2）求斜坡CD的长度.‎ ‎（第21题图）‎ ‎【考点】解直角三角形的应用，三角函数.‎ ‎【分析】（1）在在Rt△ABC中，利用三角函数，可求出AC的值；‎ ‎（2）过点D作DF⊥AB于点F，则四边形AEDF为矩形；设CD=x米，表示出DE=x米，CE=x米，得出BF=DF=AB-AF=60-x，根据DF=AE=AC+CE列解方程即可. ‎ ‎【解答】解：（1）在Rt△ABC中，AB=60米，∠ACB=60°，‎ ‎ ∴AC==20米. ‎ ‎（2）过点D作DF⊥AB于点F，则四边形AEDF为矩形，‎ ‎ ∴AF=DE，DF=AE ‎ 设CD=x米，在Rt△CDE中，DE=x米，CE=x米 在Rt△BDF中，∠BDF=45°，‎ ‎∴BF=DF=AB-AF=60-x（米）‎ ‎∵DF=AE=AC+CE，‎ ‎∴20+x=60-x 解得：x=80-120（米）‎ ‎（或解：作BD的垂直平分线MN，构造30°直角三角形，由BC=40解方程可得CD=80-120）‎ 答：（1）坡底C点到大楼距离AC的值为20米；（2）斜坡CD的长度为80-120米.‎ ‎【点评】本题考查了解直角三角形﹣仰角俯角问题、坡度坡角问题，构造直角三角形 是解本题的关键．‎ ‎22.（本题满分8分）已知直线l:y=kx+1与抛物线y=x2-4x ‎（1）求证：直线l与该抛物线总有两个交点；‎ ‎（2）设直线l与该抛物线两交点为A，B，O为原点，当k=-2时，求△OAB的面积.‎ ‎【考点】二次函数综合题.‎ ‎【分析】（1）令直线l:y=kx+1与抛物线y=x2-4x相等，得一元二次方程，求△的值即可；‎ ‎（2）设A，B的坐标分别为（x1，y1），（x2，y2），直线l与y轴交点为C（0，1）,根据根与系数的关系得到|x1-x2|的长，即可求出面积.‎ ‎【解答】（1）证明：令x2-4x= kx+1，则x2-(4+k)x-1=0‎ ‎∴△= (4+k)2+4＞0，‎ ‎∴直线l与该抛物线总有两个交点；‎ ‎（2）解：设A，B的坐标分别为（x1，y1），（x2，y2），直线l与y轴交点为C（0，1）‎ 由（1）知道的：x1+x2=4+k=2, x1x2= -1‎ ‎ (x1-x2)2=4+4=8, |x1-x2|=2,‎ ‎△OAB的面积S=·OC·|x1-x2|=×1×2=.‎ ‎（或解：解方程得 x1=1-, 或 x2=1+, ‎ ‎ y1=2-1 y2= -2-1‎ ‎ 或S=×|y1-y2|=×4=. )‎ ‎【点评】本题主要考查了二次函数与一次函数的综合应用，设A，B的坐标分别为（x1，y1），（x2，y2），利用根的判别式得出|x1-x2|是解决问题的关键．‎ ‎23.（本题满分9分）我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：y= x+4（1≤x≤8，x为整数）‎ ‎ -x+20（9≤x≤12，x为整数），每件产品的利润z（元）与月份x（月）的关系如下表：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ z ‎19‎ ‎18‎ ‎17‎ ‎16‎ ‎15‎ ‎14‎ ‎13‎ ‎12‎ ‎11‎ ‎10‎ ‎10‎ ‎10‎ ‎（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；‎ ‎（2）若月利润w（万元）=当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；‎ ‎（3）当x为何值时，月利润w有最大值，最大值为多少？‎ ‎【考点】二次函数的应用、一次函数的应用.‎ ‎【分析】（1）根据表格,分两种情形作答即可．‎ ‎（2）分三种情形写出月利润w（万元）与月份x（月）的关系式即可．‎ ‎（3）分三种情形求出月利润w的最大值，再比较即可．‎ ‎【解答】解：（1）根据表格可知：当1≤x≤10的整数时，z= -x+20；‎ ‎ 当11≤x≤12的整数时，z=10；‎ ‎∴z与x的关系式为： -x+20（1≤x≤10，x为整数）‎ ‎ Z= ‎ ‎ 10（11≤x≤12，x为整数）‎ ‎（2）当1≤x≤8时，w=（-x+20）（x+4）=-x2+16x+80‎ 当9≤x≤10时，w=（-x+20）（-x+20）=x2-40x+400；‎ 当11≤x≤12时，w=10（-x+20）=-10x+200；‎ ‎ -x2+16x+80(1≤x≤8，x为整数)‎ ‎∴w与x的关系式为： w= x2-40x+400(9≤x≤10，x为整数) ‎ ‎-10x+200(11≤x≤12，x为整数)‎ ‎（3）当1≤x≤8时，w=-x2+16x+80=-（x-8）2+144，‎ ‎ ∴x=8时，w有最大值144.‎ 当9≤x≤10时，w=x2-40x+400= (x-20)2.‎ W随x增大而减小，∴x=9时，w有最大值121.‎ 当11≤x≤12时，w=-10x+200,‎ W随x增大而减小，∴x=11时，w有最大值90.‎ ‎∵90＜121＜144‎ ‎∴x=8时，w有最大值144.‎ ‎【点评】本题主要考查了二次函数的应用、一次函数的应用．分类讨论和熟练掌握函数的性质是解决本题的关键.‎ ‎24.（本题满分14分）如图，在直角坐标系XOY中，菱形OABC的边OA在x轴正半轴上，点B，C在第一象限，∠C=120°，边长OA=8，点M从原点O出发沿x轴正半轴以每秒1个单位长的速度作匀速运动，点N从A出发沿边AB—BC—‎ CO以每秒2个单位长的速度作匀速运动。过点M作直线MP垂直于x轴并交折线OCB于P，交对角线OB于Q，点M和点N同时出发，分别沿各自路线运动，点N运动到原点O时，M和N两点同时停止运动。‎ ‎（1）当t=2时，求线段PQ的长；‎ ‎（2）求t为何值时，点P与N重合；‎ ‎（3）设△APN的面积为S，求S与t的函数关系式及t的取值范围. ‎ ‎【考点】四边形综合题.‎ ‎【分析】（1）当t=2时，利用特殊角的三角函数值，可求出线段PQ的长；‎ ‎（2）由OA=8知，当t≤4时，AN=PO=2OM=2t，t=4时，P到达C点，N到达B点，点P，N在边BC上相遇。设t秒时，点P与N重合，则(t-4)+2(t-4)=8, 即可求出t；‎ ‎（3）分0≤t≤4、4＜t≤、＜t≤8、8＜t≤12讨论。‎ ‎【解答】解：（1）在菱形OABC中，∠AOC=60°，∠AOQ=30°，‎ 当t=2时，OM=2，PM=2，QM=，PQ=.‎ ‎（2）当t≤4时，AN=PO=2OM=2t，‎ ‎ t=4时，P到达C点，N到达B点，点P，N在边BC上相遇。‎ ‎ 设t秒时，点P与N重合，则(t-4)+2(t-4)=8, ‎ ‎∴t=.‎ 即t=秒时，点P与N重合.‎ ‎（3）①当0≤t≤4时，PN=OA=8，且PN∥OA，PM=t，‎ S△APN=·8·t=4t；‎ ‎ ‎ ‎②当4＜t≤时，PN=8-3(t-4)=20-3t，‎ S△APN=×4×(20-3t)=40-6t；‎ ‎③当＜t≤8时，PN=3(t-4)-8=3t-20，‎ S△APN=×4×(3t-20)= 6t -4；‎ ‎④8＜t≤12时，ON=24-2t，N到OM距离为12-t,‎ ‎ N到CP距离为4-(12-t)= t-8，CP=t-4，BP=12-t，‎ S△APN=S菱形-S△AON- S△CPN- S△APB ‎ =32-×8×(12-t)- （t-4）（t-8）-（12-t）×4‎ ‎ = - t2+12t-56‎ 综上，S与t的函数关系式为：‎ ‎4t（0≤t≤4）‎ ‎40-6t（4＜t≤）‎ S= 6t -4（＜t≤8）‎ ‎- t2+12t-56（8＜t≤12）‎ ‎（注：在第一段定义域写为0＜t≤4，第二段函数的定义域写为4＜4＜照样给满分）‎ ‎【点评】本题主要考查了四边形综合运用，涉及面积问题、动点问题．分类讨论是解决本题的关键. 题目的综合性较强，难度中等．‎