2011年全国各地100份中考数学试卷分类汇编第25--多边形与平行四边形 9页

‎2011年全国各地100份中考数学试卷分类汇编 第25章 多边形与平行四边形 一、选择题 ‎1. （2011安徽，6，4分）如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（ ）‎ A．7 B．‎9 ‎ C．10 D．11‎ ‎【答案】D ‎ ‎2. （2011广东广州市，2，3分）已知□ABCD的周长为32，AB=4，则BC=（ ）.‎ A.4 B‎.12 ‎ C.24 D.28‎ ‎【答案】B ‎3. （2011山东威海，3，3分）在□ABCD中，点E为AD的中点，连接BE，交AC于点F，则AF：CF＝（ ） ‎ A．1：2 B．1：‎3 ‎ C．2：3 D．2：5 ‎ ‎【答案】A ‎4. （2011四川重庆，9，4分）下面图形都是由同样大小的平行四边形按一定的规律组成，其中，第①个图形一共有1个平行四边形，第②个图形一共有5个平行四边形，第③个图形一共有11个平行四边形，……，则第⑥个图形中平行四边形的个数为( )‎ ‎……‎ 图① 图② 图③ 图④‎ A．55 B．42 C．41 D．29‎ ‎【答案】C ‎5. 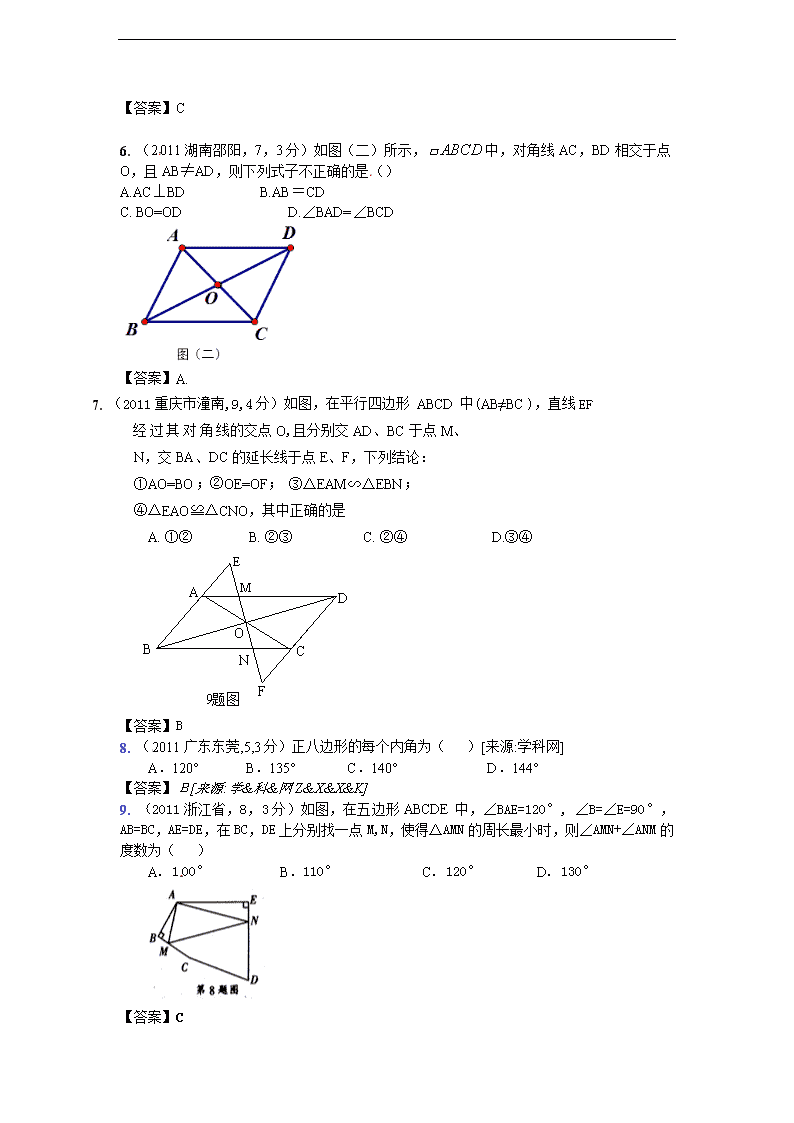（2011江苏泰州，7，3分）四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC．其中一定能判定这个四边形是平行四边形的条件有 ‎ A．1组 B．2组 C．3组 D．4组 ‎ ‎【答案】C ‎6. （2011湖南邵阳，7，3分）如图（二）所示，中，对角线AC，BD相交于点O，且AB≠AD，则下列式子不正确的是（）‎ A.AC⊥BD B.AB＝CD ‎ C. BO=OD D.∠BAD=∠BCD ‎【答案】A.‎ ‎7. （2011重庆市潼南,9,4分）如图，在平行四边形 ABCD中(AB≠BC)，直线EF 经过其对角线的交点O,且分别交AD、BC于点M、‎ N，交BA、DC的延长线于点E、F，下列结论：‎ ‎①AO=BO；②OE=OF； ③△EAM∽△EBN；‎ ‎④△EAO≌△CNO，其中正确的是 A. ①② B. ②③ C. ②④ D.③④‎ ‎【答案】B ‎8. （2011广东东莞,5,3分）正八边形的每个内角为（ ）[来源:学科网]‎ A．120° B．135° C．140° D．144°‎ ‎【答案】Ｂ[来源:学&科&网Z&X&X&K]‎ ‎9. （2011浙江省，8，3分）如图，在五边形ABCDE中，∠BAE=120°, ∠B=∠E=90°，AB=BC，AE=DE，在BC，DE上分别找一点M,N，使得△AMN的周长最小时，则∠AMN+∠ANM的度数为（ ）‎ A. 100° B．110° C. 120° D. 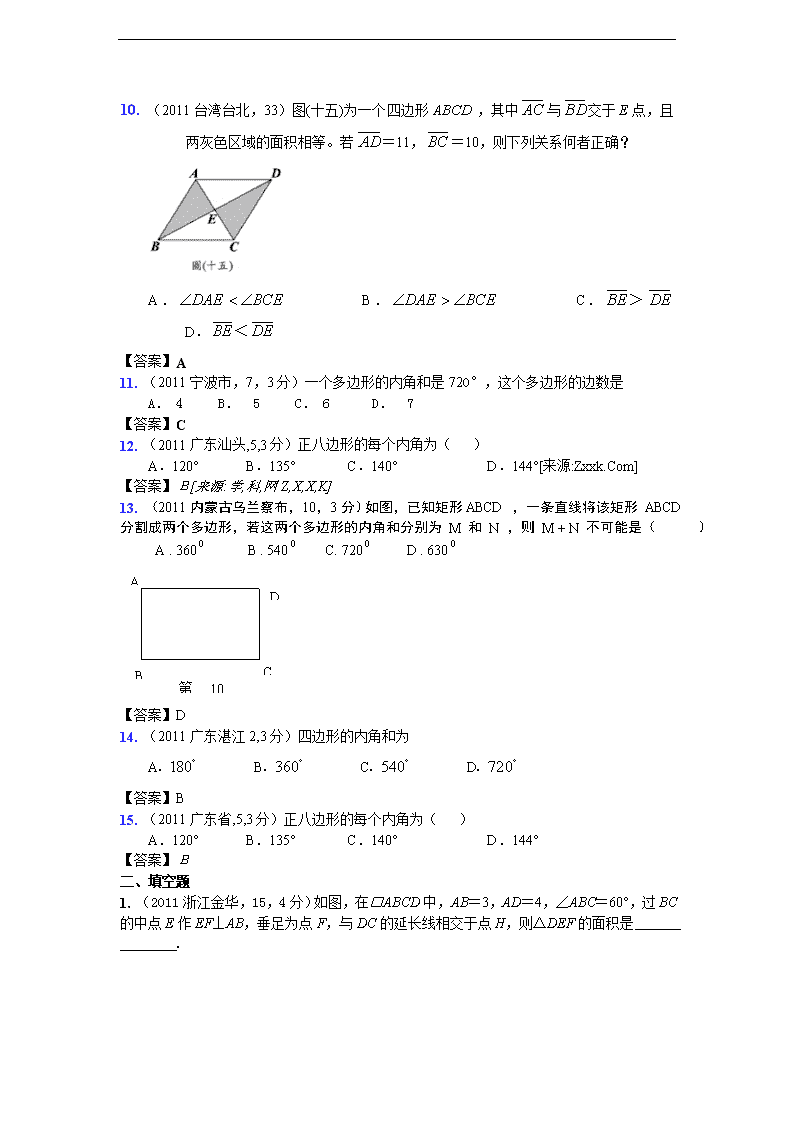130°‎ ‎ ‎ ‎【答案】C ‎10. （2011台湾台北，33）图(十五)为一个四边形，其中与交于E点，且两灰色区域的面积相等。若＝11，＝10，则下列关系何者正确？‎ A． B． C．＞ D．＜‎ ‎【答案】A ‎11. （2011宁波市，7，3分）一个多边形的内角和是720°，这个多边形的边数是 ‎ A． 4 B． ‎5 C． 6 D． 7‎ ‎【答案】C ‎12. （2011广东汕头,5,3分）正八边形的每个内角为（ ）‎ A．120° B．135° C．140° D．144°[来源:Zxxk.Com]‎ ‎【答案】Ｂ[来源:学,科,网Z,X,X,K]‎ ‎13. （2011内蒙古乌兰察布，10，3分）如图，已知矩形ABCD ，一条直线将该矩形 ABCD 分割成两个多边形，若这两个多边形的内角和分别为 M 和 N ，则 M + N 不可能是（ ）‎ A . 360 B . ‎540‎ C. 720 D . 630‎ A C B D 第10题图 ‎【答案】D ‎14. （2011广东湛江2,3分）四边形的内角和为 A B C D ‎ ‎【答案】B ‎15. （2011广东省,5,3分）正八边形的每个内角为（ ）‎ A．120° B．135° C．140° D．144°‎ ‎【答案】Ｂ 二、填空题 ‎1. （2011浙江金华，15，4分）如图，在□ABCD中，AB＝3，AD＝4，∠ABC＝60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是 .‎ ‎【答案】2 ‎2. （2011山东德州10,4分）如图，D，E，F分别为△ABC三边的中点，‎ 则图中平行四边形的个数为___________．‎ A B C D E F 第10题图 ‎【答案】3‎ ‎3. （2011浙江丽水，15，4分）如图，在□ABCD中，AB＝3，AD＝4，∠ABC＝60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是 .[来源:学科网]‎ ‎【答案】2 ‎4. （2011江苏苏州，12,3分）如图，在四边形ABCD中，AB∥CD，AD∥BC，AC、BD相交于点O.若AC=6，则线段AO的长度等于___________.‎ ‎【答案】3‎ ‎5. （2011山东聊城，14，3分）如图，在□ABCD中，AC、BD相交于点O，点E是AB的中点，OE＝‎3cm，则AD的长是__________cm．‎ ‎【答案】6‎ ‎6. （2011山东临沂，18，3分）如图，□ ABCD中，E是BA延长线上一点，AB＝AE，连结CE交AD于点F，若CF平分∠BCD，AB＝3，则BC的长为 ．‎ ‎【答案】6[来源:学#科#网]‎ ‎7. （2011湖南常德，4，3分）四边形的外角和为__________.‎ ‎【答案】360°‎ ‎8. （2011四川广安，16，3分）若凸边形的内角和为1260°，则从一个顶点出发引的对角线条数是____‎ ‎【答案】6‎ 三、解答题 ‎1. （2011浙江义乌，18，6分）如图，已知E、F是□ABCD对角线AC上的两点，‎ 且BE⊥AC，DF⊥AC.‎ ‎[来源:学科网]‎ F E A B C D ‎（1）求证：△ABE≌△CDF；‎ ‎（2）请写出图中除△ABE≌△CDF外其余两对全等 三角形（不再添加辅助线）．‎ ‎【答案】（1）∵四边形ABCD是平行四边形 ‎∴AB=CD AB∥CD ‎ ‎∴∠BAE=∠FCD 又∵BE⊥AC DF⊥AC ‎ ∴∠AEB=∠CFD=90°‎ ‎∴△ABE≌△CDF （AAS）‎ ‎ （2）①△ABC≌△CDA ②△BCE≌△DAF ‎2. （2011湖南常德，21，7分）如图5，已知四边形ABCD是平行四边形.‎ ‎ （1）求证：△MEF ∽△MBA；‎ ‎ （2）若AF，BE分别，∠CBA的平分线，求证DF=EC A 图5‎ B C D E F M ‎【答案】‎ （1） 证明：在□ABCD中，CD∥AB ‎ ∴∠MEF=∠MBA，∠MFE=∠MAB ‎ ∴△MEF ∽△MBA （2） 证明：∵在□ABCD中，CD∥AB ‎∠DFA=∠FAB 又∵AF是∠DAB的平分线[来源:学。科。网]‎ ‎∴∠DAF=∠FAB ‎∴∠DAF=∠DFA ‎∴AD=DF 同理可得EC=BC ‎∵在□ABCD中，AD=BC ‎∴DF=EC ‎3. （2011四川成都，20,10分） 如图，已知线段AB∥CD，AD与BC相交于点K，E是线段AD上一动点.‎ ‎ (1)若BK=KC，求的值；‎ ‎ (2)连接BE，若BE平分∠ABC，则当AE=AD时，猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明．再探究：当AE=AD ()，而其余条件不变时，线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论，不必证明．[来源:Zxxk.Com]‎ ‎【答案】解：（1）∵AB∥CD，BK=KC，∴==.‎ ‎（2）如图所示，分别过C、D作BE∥CF∥DG分别交于AB的延长线于F、G三点，‎ ‎∵BE∥DG，点E是AD的点，∴AB=BG；∵CD∥FG，CD∥AG，∴四边形CDGF 是平行四边形，∴CD=FG；‎ ‎∵∠ABE=∠EBC ，BE∥CF，∴∠EBC=∠BCF，∠ABE=∠BFC，∴BC=BF，‎ ‎∴AB-CD=BG-FG=BF=BC，∴AB=BC+CD.‎ 当AE=AD ()时，（）AB=BC+CD.‎ ‎4. （2011四川宜宾,17⑶,5分）如图，平行四边形ABCD的对角线AC、BD交于点O，E、F在AC上，G、H在BD上，AF=CE，BH=DG．‎ 求证：GF∥HE． ‎ H A ‎（17（3）题图）‎ C B D O E G F ‎【答案】证明：∵平行四边形ABCD中，OA=OC，‎ 由已知：AF=CE AF－OA=CE－OC ∴OF=OE 同理得：OG=OH ‎∴四边形EGFH是平行四边形 ‎∴GF∥HE ‎5. （2011江苏淮安，20，8分）如图，四边形ABCD是平行四边形，EF分别是BC、AD上的点，∠1=∠2.‎ 求证：△ABE≌△CDF.‎ ‎【答案】∵四边形ABCD是平行四边形，‎ ‎∴∠B=∠D，AB=DC，‎ 又∵∠1=∠2，‎ ‎∴△ABE≌△CDF（ASA）.‎ ‎6. （2011四川凉山州，20，7分）如图，是平行四边形的对角线上的点，，请你猜想：线段与线段有怎样的关系？并对你的猜想加以证明。[来源:Zxxk.Com]‎ B C D E F A ‎20题图 ‎【答案】猜想：。‎ ‎ 证明： ∵四边形ABCD是平行四边形 ‎ ‎ ∴，∥ ‎ ‎ ∴ ‎ ‎ 在和 ‎ ‎ ‎ ∴≌ ‎ ‎ ∴，‎ ‎ ∴∥‎ 即 。‎ ‎7. （2011江苏无锡，21，8分）(本题满分8分)如图，在□ABCD中，E、F为对角线BD上的两点，且∠BAE=∠DCF．‎ ‎ 求证：BE = DF．‎ B C D A E F ‎【答案】证明：∵□ABCD中，AB = CD，AB // CD，…………………………………………(2分)‎ ‎ ∴∠ABE = ∠CDF，……………………………………………………………(4分)‎ ‎ 又∵∠BAE = ∠DCF，∴△ABE≌△CDF，………………………………(6分)‎ ‎ ∴BE = DF．…………………………………………………………………(8分)‎ ‎8. （2011湖南永州，21，8分）如图，BD是□ABCD的对角线，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．‎ 求证：△ABE≌△CDF．‎ ‎（第21题）‎ ‎【答案】证明：□ABCD中，AB=CD，∠A=∠C， AB∥CD ∴∠ABD=∠CDB ‎∵∠ABE=∠ABD,∠CDF=∠CDB ∴∠ABE=∠CDF 在△ABE与△CDF中 ‎ ‎∴△ABE≌△CDF．‎