2020九年级数学下册 第2章 直线与圆的位置关系 专题分类突破六 切线的判定与性质应用的基本图形练习 （新版）浙教版 7页

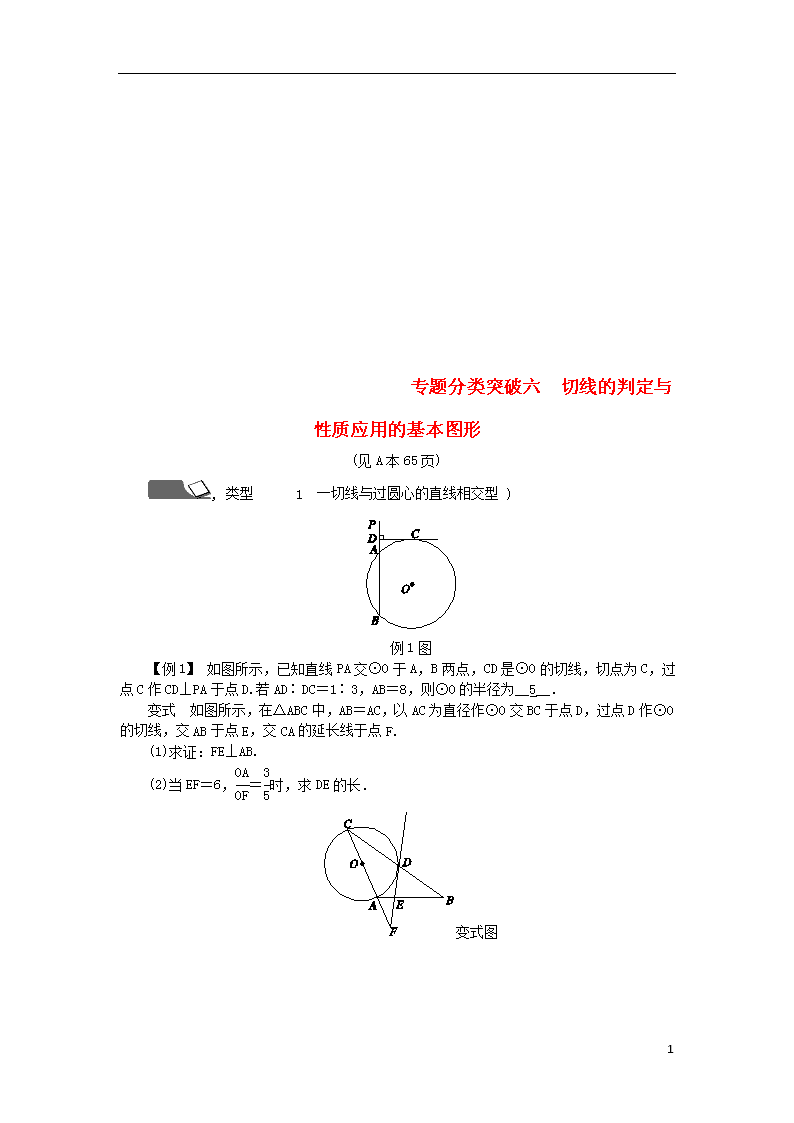
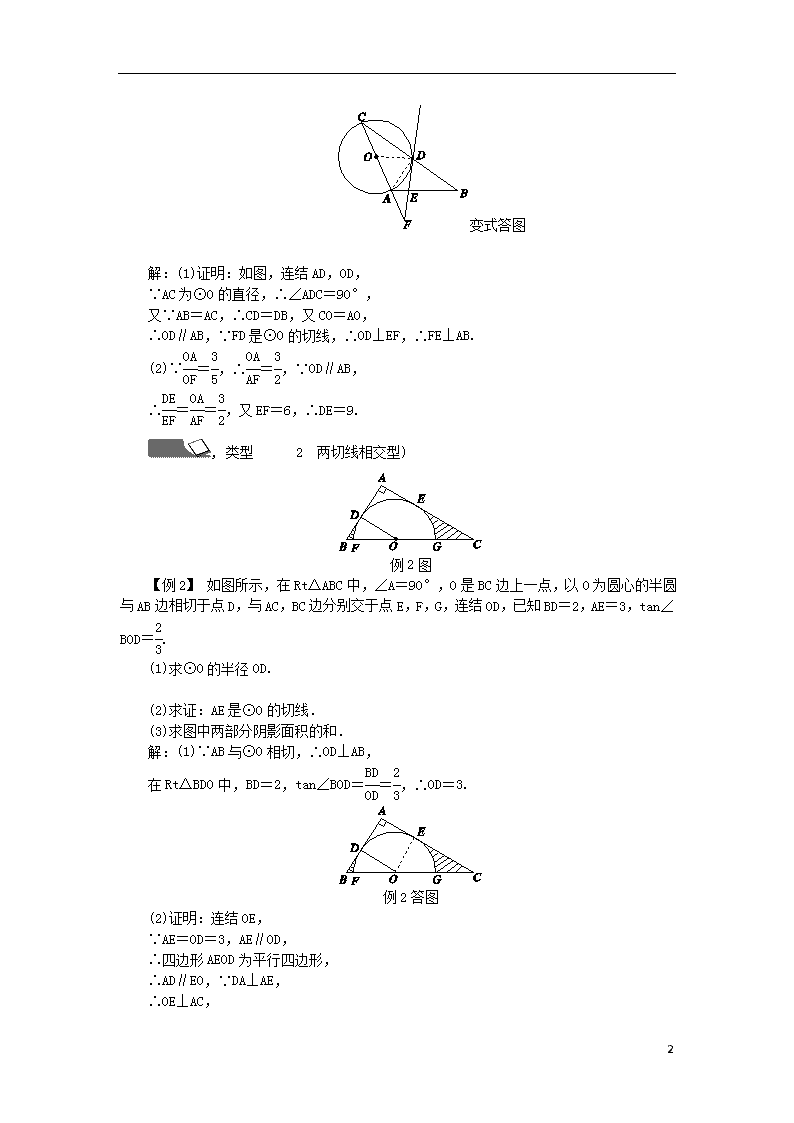
专题分类突破六　切线的判定与性质应用的基本图形 ‎(见A本65页)‎ ‎, 类型　　　1　一切线与过圆心的直线相交型 )‎ 例1图 ‎【例1】 如图所示，已知直线PA交⊙O于A，B两点，CD是⊙O的切线，切点为C，过点C作CD⊥PA于点D.若AD∶DC＝1∶3，AB＝8，则⊙O的半径为__5__．‎ 变式　如图所示，在△ABC中，AB＝AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线，交AB于点E，交CA的延长线于点F.‎ ‎(1)求证：FE⊥AB.‎ ‎(2)当EF＝6，＝时，求DE的长．‎ 变式图 7‎ ‎　　　变式答图 解：(1)证明：如图，连结AD，OD，‎ ‎∵AC为⊙O的直径，∴∠ADC＝90°，‎ 又∵AB＝AC，∴CD＝DB，又CO＝AO，‎ ‎∴OD∥AB，∵FD是⊙O的切线，∴OD⊥EF，∴FE⊥AB.‎ ‎(2)∵＝，∴＝，∵OD∥AB，‎ ‎∴＝＝，又EF＝6，∴DE＝9.‎ ‎, 类型　　　2　两切线相交型)‎ 例2图 ‎【例2】 如图所示，在Rt△ABC中，∠A＝90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC，BC边分别交于点E，F，G，连结OD，已知BD＝2，AE＝3，tan∠BOD＝.‎ ‎(1)求⊙O的半径OD.‎ ‎(2)求证：AE是⊙O的切线．‎ ‎(3)求图中两部分阴影面积的和．‎ 解：(1)∵AB与⊙O相切，∴OD⊥AB，‎ 在Rt△BDO中，BD＝2，tan∠BOD＝＝，∴OD＝3.‎ 例2答图 ‎(2)证明：连结OE，‎ ‎∵AE＝OD＝3，AE∥OD，‎ ‎∴四边形AEOD为平行四边形，‎ ‎∴AD∥EO，∵DA⊥AE，‎ ‎∴OE⊥AC，‎ 7‎ 又∵OE为圆的半径，∴AE为⊙O的切线．‎ ‎(3)∵OD∥AC，‎ ‎∴＝，即＝，‎ ‎∴AC＝7.5，∴EC＝AC－AE＝7.5－3＝4.5，‎ ‎∴S阴影＝S△BDO＋S△OEC－S扇形FOD－S扇形EOG ‎＝×2×3＋×3×4.5－ ‎＝3＋－＝.‎ ‎, 类型　　　3　由图形的变换生成的相切问题)‎ 例3图 ‎【例3】 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y＝kx＋4与x轴、y轴分别交于点A，B，∠OAB＝30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P的个数是(　A　)‎ A．6　 　 B．‎8　‎ 　 C．10　 　 D．12‎ 变式图 变式　如图所示，在矩形ABCD中，AB＝2，BC＝4，⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则tan∠EFO的值为____．‎ ‎1．如图所示，矩形ABCD的长为6，宽为3，点O1为矩形的中心，⊙O2的半径为1，O1O2⊥AB于点P，O1O2＝6.若⊙O2绕点P按顺时针方向旋转360°，在旋转过程中，⊙O2与矩形的边只有一个公共点的情况一共出现(　B　)‎ 第1题图 7‎ A．3次　　 B．4次　　 C．5次　　 D．6次 ‎2．如图所示，直线l与以线段AB为直径的圆相切于点C，AB＝6，AC＝3，点P是直线l上一个动点．当∠APB的度数最大时，线段BP的长度为(　D　)‎ A．6 B．‎6‎ C．9 D．3 第2题图 ‎　　　第3题图 ‎3．如图所示，在△ABC中，BC＝‎8 cm，以A为圆心、‎2 cm为半径的圆与BC相切于点D，交AB于点E，交AC于点F，点P在圆上，∠EPF＝50°，则图中阴影部分的面积为__8－π__cm2.‎ 第4题图 ‎4．如图所示，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D的切线分别交AB，AC的延长线于点E，F.‎ ‎(1)求证：AF⊥EF.‎ ‎(2)小强同学通过探究发现：AF＋CF＝AB.请你帮助小强同学证明这一结论．‎ 证明：(1)如图所示，连结OD，交BC于点M，则OD⊥EF.‎ ‎∵OA＝OD，∴∠OAD＝∠ODA.‎ ‎∵∠OAD＝∠DAC，‎ ‎∴∠DAC＝∠ODA，‎ ‎∴OD∥AF，∴AF⊥EF.‎ 7‎ 第4题答图 ‎(2)如图所示，连结BD，CD，延长BD，CF交于点G，‎ ‎∵AB为直径，∴∠ADB＝90°.‎ 又∵AD平分∠BAC，‎ ‎∴AB＝AG，GD＝DB，CD＝DB.‎ ‎∴CD＝GD.‎ ‎∵AF⊥EF，∴CF＝GF，‎ ‎∴AF＋CF＝AF＋FG＝AG，∴AF＋CF＝AB.‎ 第5题图 ‎5．如图所示，已知直线y＝－x＋3分别与x轴、y轴交于A，B两点，点P是反比例函数y＝－(x＜0)图象上的一动点，PH⊥x轴于点H，若以点P为圆心，PH为半径作⊙O，当⊙O与直线AB恰好相切时，求此时OH的长．‎ 解：作PC⊥AB于点C，连结AP，‎ ‎∵直线y＝－x＋3分别与x轴、y轴交于A，B，‎ 第5题答图 当y＝0时，x＝，当x＝0时，y＝3，‎ ‎∴A(，0)，B(0，3)，‎ ‎∵∠AOB＝90°，tan∠OAB＝＝，‎ ‎∴∠OAB＝60°，‎ ‎∵以P为圆心，PH为半径的圆与直线AB相切，‎ ‎∴PH＝PC，∴AP平分∠OAB，‎ ‎∴∠PAH＝∠OAB＝30°，‎ 设OH＝x，则AH＝x＋，‎ ‎∵PH⊥x轴，∴∠PHA＝90°，‎ ‎∴tan∠PAH＝，∴PH＝AH·tan 30°＝(x＋)，‎ ‎∵点P是y＝－(x＜0)的图象上一点，‎ ‎∴PH·OH＝，即(x＋)x＝，‎ 7‎ 解得x＝(负值舍去)，‎ ‎∴OH＝.‎ ‎6．已知I是△ABC的内心，AI延长线交△ABC外接圆于D，连结BD.‎ ‎(1)在图1中，求证：DB＝DI.‎ ‎(2)如图2，若AB为直径，且OI⊥AD于I点，DE切圆于D点，求sin∠ADE的值．‎ 第6题图 解：(1)证明：如图1，连结BI，‎ ‎∵I是△ABC的内心，‎ ‎∴AD平分∠CAB，BI平分∠ABC，‎ ‎∴∠CAD＝∠BAD，∠ABI＝∠CBI，‎ ‎∵∠CAD＝∠DBC，∴∠DAB＝∠CBD，‎ ‎∵∠DBI＝∠DBC＋∠CBI，‎ ‎∠DIB＝∠DAB＋∠IBA，‎ ‎∴∠DIB＝∠DBI，∴BD＝DI；‎ ‎(2)如图2，连结BD，‎ ‎∵AB为直径，∴∠ADB＝90°，‎ ‎∵OI⊥AD，∴AD＝2DI，‎ ‎∵BD＝DI，∴AD＝2BD，‎ ‎∴AB＝＝BD，‎ ‎∵DE切圆于D点，∴∠ABD＝∠ADE，‎ ‎∴sin∠ADE＝sin∠ABD＝＝.‎ 第6题答图 7‎ 7‎