2020九年级数学上册 复习课三（4 6页

复习课三 (4.1－4.4)‎ ‎【知识点1】比例线段 ‎1．已知3x＝5y，则＝________．‎ ‎2．已知三个数4，9，x，其中一个数是另两个数的比例中项，则x＝____________．‎ ‎3．线段AB＝‎10cm，点P是AB的黄金分割点，则AP＝________________．‎ ‎4．若‎2a＝3b＝‎4c，且abc≠0，则的值是( )‎ A．2 B．－‎2 C．3 D．－3‎ ‎5．比例尺为1∶500的图纸上的大桥的长度约为‎1.04m，则大桥的实际长度约是( )‎ A．‎104m B．‎1040m C．‎5200m D．‎‎520m ‎【知识点2】平行线分线段成比例定理 ‎6．如图，DF∥AC，DE∥BC，下列各式中正确的是( )‎ 第6题图 A.＝ B.＝ C.＝ D.＝ ‎【知识点3】相似三角形的判定 ‎7．已知如图1、图2中各有两个三角形，其边长和角的度数已在图上标注，图2中AB、CD交于O点，对于各图中的两个三角形而言，下列说法正确的是( )‎ 第7题图 A．都相似 B．都不相似 C．只有图1相似 D．只有图2相似 6‎ ‎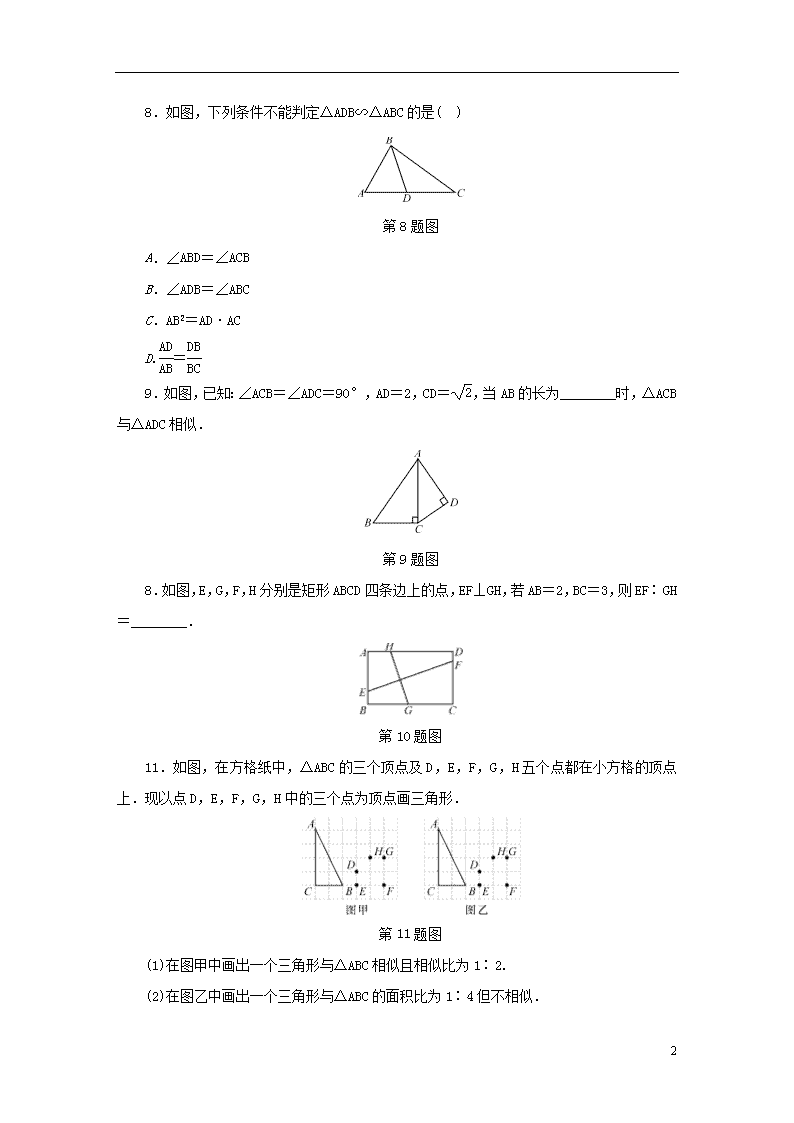8．如图，下列条件不能判定△ADB∽△ABC的是( )‎ 第8题图 A．∠ABD＝∠ACB B．∠ADB＝∠ABC C．AB2＝AD·AC D.＝ ‎9．如图，已知：∠ACB＝∠ADC＝90°，AD＝2，CD＝，当AB的长为________时，△ACB与△ADC相似．‎ 第9题图 8． 如图，E，G，F，H分别是矩形ABCD四条边上的点，EF⊥GH，若AB＝2，BC＝3，则EF∶GH＝________．‎ 第10题图 ‎11．如图，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点都在小方格的顶点上．现以点D，E，F，G，H中的三个点为顶点画三角形．‎ 第11题图 ‎(1)在图甲中画出一个三角形与△ABC相似且相似比为1∶2.‎ ‎(2)在图乙中画出一个三角形与△ABC的面积比为1∶4但不相似．‎ 6‎ ‎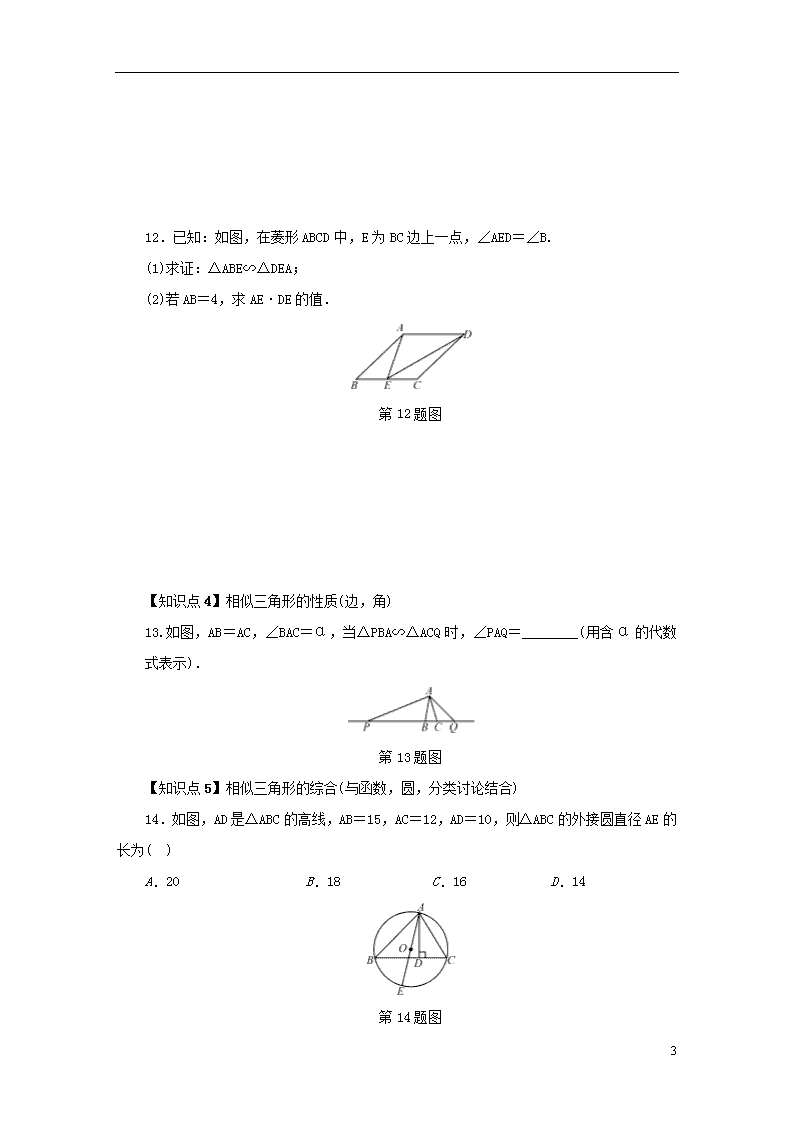12．已知：如图，在菱形ABCD中，E为BC边上一点，∠AED＝∠B.‎ ‎(1)求证：△ABE∽△DEA；‎ ‎(2)若AB＝4，求AE·DE的值．‎ 第12题图 ‎【知识点4】相似三角形的性质(边，角)‎ ‎13.如图，AB＝AC，∠BAC＝α，当△PBA∽△ACQ时，∠PAQ＝________(用含α的代数式表示)．‎ 第13题图 ‎【知识点5】相似三角形的综合(与函数，圆，分类讨论结合)‎ ‎14．如图，AD是△ABC的高线，AB＝15，AC＝12，AD＝10，则△ABC的外接圆直径AE的长为( )‎ A．20 B．‎18 C．16 D．14‎ 第14题图 6‎ ‎15.如图，△ABC中，AB＝AC＝2，∠BAC＝20°，动点P、Q分别在直线BC上运动，且始终保持∠PAQ＝100°.设BP＝x，CQ＝y，则y与x之间的函数关系用图象大致可表示为( )‎ 第15题图 ‎16．如图，在Rt△ABC中，∠C＝90°，AB＝‎10cm，AC∶BC＝4∶3，点P从点A出发沿AB方向向点B运动，速度为‎1cm/s，同时点Q从点B出发沿B→C→A方向向点A运动，速度为‎2cm/s，当一个运动点到达终点时，另一个运动点也随之停止运动．‎ ‎(1)设点P的运动时间为x(秒)，△PBQ的面积为y(cm2)，当△PBQ存在时，求y与x的函数关系式，并写出自变量x的取值范围；‎ ‎(2)当x＝5秒时，在直线PQ上是否存在一点M，使△BCM的周长最小，若存在，求出最小周长，若不存在，请说明理由．‎ ‎(3)当点Q在BC边上运动时，是否存在x，使得以△PBQ的一个顶点为圆心作圆时，另外两个顶点均在这个圆上，若存在，求出x的值；若不存在，请说明理由．‎ 第16题图 ‎17.如图，正△ABC的边长为6，点D是BC边上一点，连结AD，将AD绕点A顺时针旋转60°得AE，连结DE交AB于点F.‎ ‎(1)填空：若∠BAD＝20°，则∠BDF＝________°；‎ ‎(2)若当点D在线段BC上运动时(不与B、C两点重合)，设BD＝x，BF＝y，‎ 6‎ 试求y与x之间的函数关系式；‎ ‎(3)若＝，请求出AE的长．‎ 第17题图 复习课三 (4.1－4.4)‎ 1. 　‎ 2. ‎±6或或　‎ 3. ‎(5－5)cm或(15－5)cm ‎4－8. BDDAD　‎ 8． ‎3或3　‎ 9． ‎3∶2　‎ 10． ‎(1)如图甲所示；　(2)如图乙所示．‎ 第11题图 ‎12．(1)由条件知：∵∠AED＝∠B，∠AEB＝∠EAD，∴△ABE∽△DEA.　(2)∵△ABE∽△DEA，∴＝，∴AE·ED＝AB·AD.四边形ABCD是菱形，AB＝AD＝4，∴AE·DE＝4×4＝16.‎ ‎13.＋90°　‎ ‎14－15.BA 6‎ 第16题图 16． ‎(1)①当点Q在边BC上运动时．y＝－x2＋8x(0＜x≤3)，②当点Q在边CA上运动时，y＝(10－x)·(14－2x)＝x2－x＋42(3＜x＜7)；　(2)存在．理由：∵AQ＝14－2x＝14－10＝4，AP＝x＝5，∵AC＝8，AB＝10，∴PQ是△ABC的中位线，∴PQ∥BC，∴PQ⊥AC，∴PQ是AC的垂直平分线，∴PC＝AP＝5，∴当点M与P重合时，△BCM的周长最小，∴△BCM的周长为：MB＋BC＋MC＝PB＋BC＋PC＝5＋6＋5＝16.∴△BCM的周长最小值为16.　(3)由题意得△PBQ为等腰三角形．①PQ＝PB，x＝＞3(舍)，②BQ＝BP，x＝＞3(舍)，③QP＝QB，x＝，综上所述，存在满足题意的x，x＝.　‎ 17． ‎(1)40　(2)∵∠EDA＝60°，∴∠BDF＋∠ADC＝120°，∵∠ACB＝60°，∴∠ADC＋∠DAC＝120°，∴∠BDF＝∠DAC，∴△BDF∽△CAD，∴＝，∵BF＝y，BD＝x，AB＝BC＝AC＝6，∴＝，∴y＝－x2＋x；　‎ 第17题图 ‎(3)过点D作DG⊥AC于G，如图，∵BC＝6，＝，∴BD＝2，CD＝4，∵∠ACB＝60°，∴CG＝2，DG＝2，∴AG＝4，∴AD＝2，∵△AED是等边三角形，∴AE＝AD＝2.‎ 6‎