2014年山东省日照市中考数学试题（含答案） 15页

‎ 试卷类型:A ‎2014年日照市初中学生学业考试 数 学 试 题 ‎（总分120分 考试时间120分钟） ‎ 注意事项：‎ ‎1． 本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷3页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共11页．‎ ‎2． 答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上，考试结束，试题和答题卡一并收回．‎ ‎3． 第Ⅰ卷每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．‎ ‎4． 考试时，不允许使用科学计算器．‎ 第Ⅰ卷（选择题 共36分） ‎ 一、选择题：本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来．每小题选对得3分,选错、不选或选出的答案超过一个均记零分． ‎ ‎1．的相反数是 ( )‎ A． B． - ‎ C． 3 D． -3‎ ‎2． 下列运算正确的是（ ）‎ A． B．‎ C． D． ‎ ‎3． 下列图形中，是中心对称图形的是 ( )‎ ‎ ‎ A． B． C． D． ‎ ‎4、下图能说明∠1＞∠2的是( ) ‎ ‎1‎ ‎2‎ ‎)‎ A.‎ ‎2‎ ‎1‎ ‎)‎ D.‎ ‎1‎ ‎2‎ ‎)‎ ‎)‎ B.‎ ‎1‎ ‎2‎ ‎)‎ ‎)‎ C.‎ ‎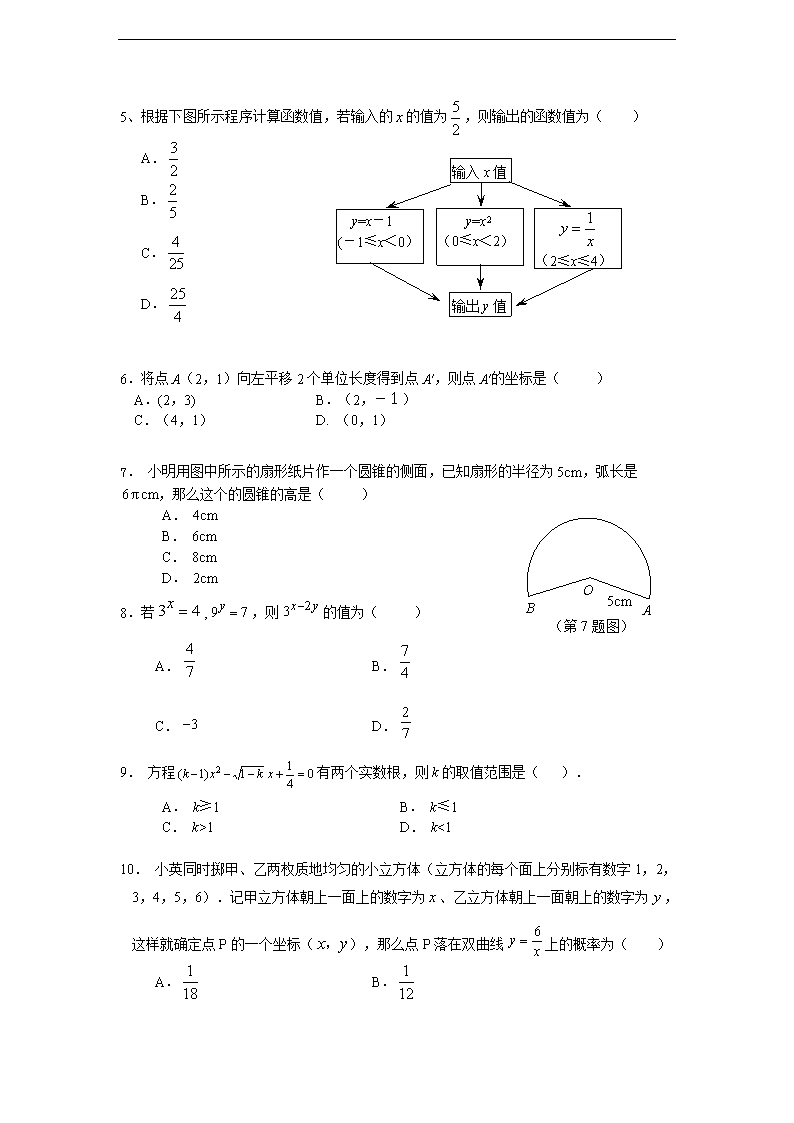5、根据下图所示程序计算函数值，若输入的的值为，则输出的函数值为（ ）‎ 输入x值 y=x－1‎ ‎(－1≤x＜0）‎ ‎（2≤x≤4）‎ y=x2‎ ‎（0≤x＜2）‎ 输出y值 A．　　　　 ‎ B． ‎ C．　 　　 ‎ D．‎ ‎6．将点A（2，1）向左平移2个单位长度得到点A′，则点A′的坐标是（ ）‎ ‎ A．(2，3) B．（2，－１） ‎ C．（4，1） D. 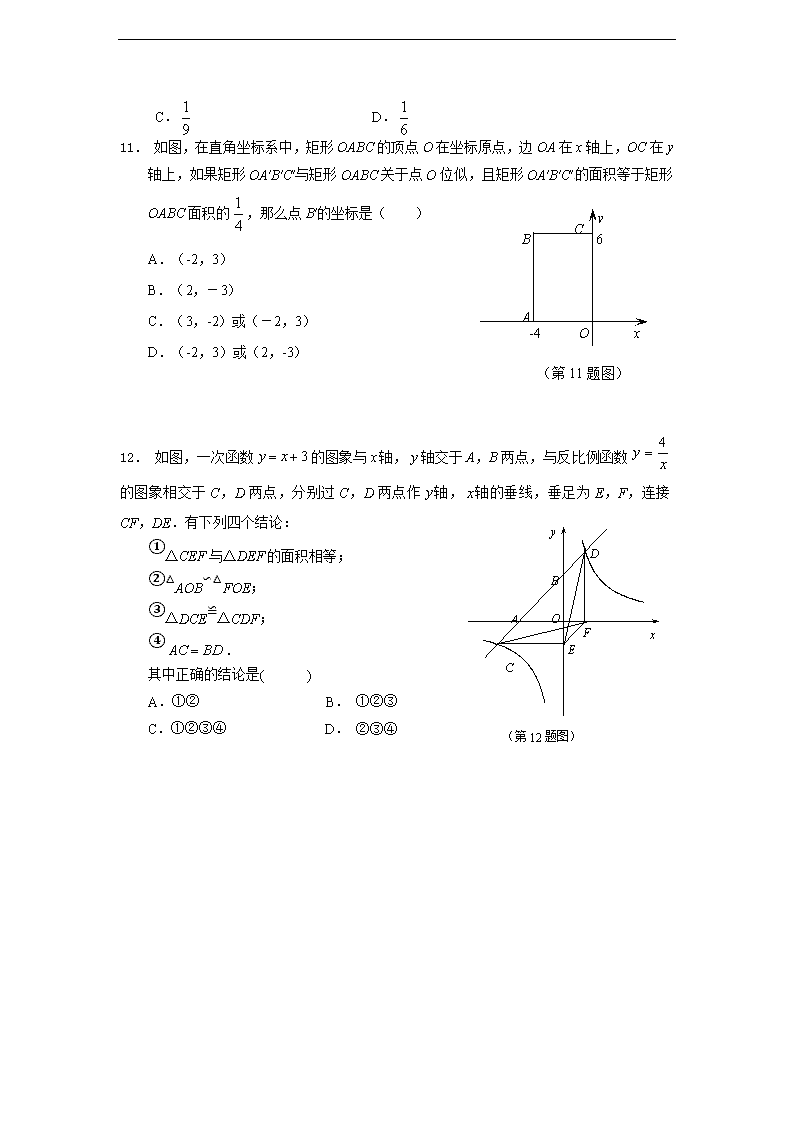（0，1）‎ ‎7． 小明用图中所示的扇形纸片作一个圆锥的侧面，已知扇形的半径为5cm，弧长是 cm，那么这个的圆锥的高是（ ）‎ O B AB ‎（第7题图）‎ ‎5cm A． 4cm ‎ B． 6cm ‎ C． 8cm ‎ D． 2cm ‎8．若,，则的值为（ ）‎ A． B． ‎ C． D．‎ ‎9． 方程有两个实数根，则k的取值范围是（ ）．‎ A． k≥1 B． k≤1 ‎ C． k>1 D． k<1‎ ‎10． 小英同时掷甲、乙两枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．记甲立方体朝上一面上的数字为、乙立方体朝上一面朝上的数字为，这样就确定点P的一个坐标（），那么点P落在双曲线上的概率为（ ）‎ ‎ A． B． ‎ C． D．‎ A B C O x y ‎-4‎ ‎6‎ ‎（第11题图）‎ ‎11． 如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的，那么点B′的坐标是（ ）‎ A．（-2，3） ‎ B．（2，－3） ‎ C．（3，-2）或（－2，3） ‎ D．（-2，3）或（2，-3）‎ y x D C A B O F E ‎（第12题图）‎ ‎12． 如图，一次函数的图象与轴，轴交于A，B两点，与反比例函数的图象相交于C，D两点，分别过C，D两点作轴，轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：‎ ‎①△CEF与△DEF的面积相等； ‎ ‎②△AOB∽△FOE；‎ ‎③△DCE≌△CDF； ‎ ‎④．‎ 其中正确的结论是( )‎ A．①② B． ①②③ ‎ C．①②③④ D． ②③④‎ ‎ 试卷类型:A ‎2014年日照市初中学生学业考试 数 学 试 题 第Ⅱ卷（非选择题 共84分）‎ 注意事项：‎ ‎　1．第Ⅱ卷共8页，用钢笔或圆珠笔直接写在试卷上．‎ ‎2．答卷前将密封线内的项目填写清楚．‎ 题号 二 三 总分 ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ 得分 得 分 评 卷 人 二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分．‎ ‎13、南海是我国固有领海，她的面积超过东海、黄海、渤海面积的总和，约为360万平方千米，360万用科学记数法可表示为 　 　　 ．‎ ‎14．分解因式： = 　 　　　 ．‎ ‎15． 某校篮球班21名同学的身高如下表：‎ 身高/cm ‎180‎ ‎185‎ ‎187‎ ‎190‎ ‎201‎ 人数/名 ‎4‎ ‎6‎ ‎5‎ ‎4‎ ‎2‎ 则该校篮球班21名同学身高的中位数是______________cm． ‎ ‎16． 某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是 cm． ‎ B D C A ‎（第16题图2）‎ ‎（第16题图1）‎ y x y=kx+b O B ‎3‎ B ‎2‎ B ‎1‎ A ‎3‎ A ‎2‎ A ‎1‎ ‎（第17题图）‎ ‎17． 在平面直角坐标系中，点，，‎ ‎，…和，，，…分别在直线 和轴上．△OA1B1，△B1A2B2，△B2A3B3，…‎ 都是等腰直角三角形，如果A1（1，1），‎ A2（），那么点的纵坐标是_ 　_____．‎ 三、解答题：本大题共7小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤． ‎ 得 分 评 卷 人 ‎18． (本题满分7分，第⑴题3分，第⑵题4分) ‎ ‎（1）计算：；‎ ‎（2）先化简，再求代数式的值,其中x是不等式组的整数解．‎ 座号 得 分 评 卷 人 ‎19． （本题满分9分）‎ 某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）． 已知A、B两组捐款人数的比为1 : 5．‎ 捐款人数分组统计图2‎ 捐款人数分组统计图1‎ ‎ 捐款人数分组统计表 组别 捐款额x/元 人数 A ‎1≤x<10‎ a B ‎10≤x<20‎ ‎100‎ C ‎20≤x<30‎ D ‎30≤x<40‎ E x≥40‎ ‎ ‎ ‎ ‎ 请结合以上信息解答下列问题．‎ ‎(1) a= ，本次调查样本的容量是 ；‎ ‎ (2) 先求出C组的人数，再补全“捐款人数分组统计图1”；‎ ‎(3) 若任意抽出1名学生进行调查，恰好是捐款数不少于30元的概率是多少？‎ 得 分 评 卷 人 ‎20． （本题满分9分）如图，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙O于点E，交AM于点D，交BN于点C，‎ ‎（1）求证：OD∥BE；‎ ‎（2）如果OD=6cm，OC=8cm，求CD的长．‎ ‎（第20题图）‎ A D ‎ N ‎ E ‎ B ‎ C ‎ O ‎ M ‎ 得 分 评 卷 人 ‎21．（本题满分9分）‎ 如图，长青化工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地．已知公路运价为1.5元/（吨·千米），铁路运价为1.2元/（吨·千米），且这两次运输共支出公路运输费15000元，铁路运输费97200元．‎ 求：（1）该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？‎ ‎（2）这批产品的销售款比原料费与运输费的和多多少元？‎ 得 分 评 卷 人 ‎22．（本题满分9分）‎ 如图某天上午9时,向阳号轮船位于A处，观测到某港口城市P位于轮船的北偏西67.5°，轮船以21海里/时的速度向正北方向行驶，下午2时该船到达B处，这时观测到城市P位于该船的南偏西36.9°方向，求此时轮船所处位置B与城市P的距离？（参考数据：sin36.9°≈，tan36.9°≈，sin67.5°≈，tan67.5°≈）‎ ‎（第22题图）‎ A P C B ‎36.9°‎ ‎67.5°‎ 得 分 评 卷 人 ‎23．（本题满分10分） ‎ ‎（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；‎ ‎（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．‎ ‎（3）运用（1）（2）解答中所积累的经验和知识，完成下题：‎ 如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求直角梯形ABCD的面积．‎ ‎（第23题图1）‎ A E B C D F ‎（第23题图3）‎ B C A D ‎ E ‎ ‎（第23题图2）‎ A E B C D G 得 分 评 卷 人 ‎24．（本题满分11分）已知抛物线经过 A（2，0）． 设顶点为点P，与x轴的另一交点为点B．‎ ‎（1）求b的值，求出点P、点B的坐标；‎ ‎（2）如图，在直线 y=x上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；‎ A P B x y O ‎（第24题图）‎ ‎（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在,试举例验证你的猜想；如果不存在，试说明理由．‎ ‎ ‎ ‎ 试卷类型:A ‎2014年日照市初中学生学业考试 数学试题参考答案与评分标准 评卷说明：‎ ‎1. 选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．‎ ‎2. 解答题中的每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．本答案对每小题只给出一种解法，对考生的其他解法，请参照评分意见进行评分．‎ ‎3. 如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分．‎ 一.选择题：本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分． ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B A B C B D A A D C D C 二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分．‎ ‎13.3.6×106； 14.x(x+3)(x－3)； 15. 187； 16. 30； 17.‎ 三、解答题：本大题共7小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤． ‎ ‎18． (本题满分7分，第⑴题3分，第⑵题4分) ‎ ‎（1）解：原式=－3－3+1+2…………………………2分 ‎ =-2-…………………………3分 ‎（2）原式=， ………………1分 解不等式组得，………………………2分 因为x是整数，所以，……………………3分 当时，原式=.……………………4分 ‎19. 解：（1）20，500；…………………………2分 ‎ （2）500×40%=200，C组的人数为200. … 4分 ‎ 补图见图． …………………………5分 ‎（3）∵D、E两组的人数和为：‎ ‎500×（28%+8%）=180，………………7分 ‎∴捐款数不少于30元的概率是：‎ ‎……………………………… 9分 ‎20.（1）证明：连接OE，‎ ‎ ∵AM、DE是⊙O的切线，OA、OE是⊙O的半径，‎ ‎∴∠ADO=∠EDO， ∠DAO=∠DEO=90°， ……………………2分 ‎（第20题答案图）‎ A D ‎ N ‎ E ‎ B ‎ C ‎ O ‎ M ‎ ‎∴∠AOD=∠EOD=∠AOE， ‎ ‎∵∠ABE=∠AOE ‎∴∠AOD=∠ABE，‎ ‎∴OD∥BE …………………5分 ‎（2）由（1）得：∠AOD=∠EOD=∠AOE，‎ ‎ 同理，有：∠BOC=∠EOC=∠BOE ‎ ∴∠AOD+∠EOD+∠BOC+∠EOC=180°‎ ‎ ∴∠EOD+∠EOC=90°，‎ ‎ ∴△DOC是直角三角形，…………………………7分 ‎ ∴ CD=……………………9分 ‎21.解：（1）设工厂从A地购买了x吨原料,制成运往B地的产品y吨.则依题意，得：‎ ‎…………………………4分 解这个方程组，得：‎ ‎ ∴工厂从A地购买了400吨原料,制成运往B地的产品300吨. ………7分 ‎ （2）依题意，得：300×8000-400×1000-15000-97200=1887800‎ ‎ ∴批产品的销售款比原料费与运输费的和多1887800元. ………………9分 ‎22．解：过点P作PC⊥AB，垂足为C，设PC=x海里．‎ ‎　　　　在Rt△APC中，∵tan∠A=，∴AC=．…………3分 ‎　　　　在Rt△PCB中，∵tan∠B=，∴BC=．…………5分 ‎ ∵AC＋BC=AB=21×5，∴，解得．‎ ‎　　　　∵，∴（海里）．‎ ‎　　　　∴向阳号轮船所处位置B与城市P的距离为100海里．………………9分 ‎（第23题答案图1）‎ A E B C D F ‎23. 解答：（1）证明：在正方形ABCD中，‎ ‎∵BC＝CD，∠B＝∠CDF，BE＝DF，‎ ‎∴△CBE≌△CDF．‎ ‎∴CE＝CF． …………………………2分 ‎（2）证明： 如图2，延长AD至F，使DF=BE．连接CF．‎ ‎ 由（1）知△CBE≌△CDF，‎ ‎∴∠BCE＝∠DCF．‎ ‎∴∠BCE＋∠ECD＝∠DCF＋∠ECD ‎（第23题答案图2）‎ A E B C D G F 即∠ECF＝∠BCD＝90°，‎ 又∠GCE＝45°，∴∠GCF＝∠GCE＝45°．‎ ‎∵CE＝CF，∠GCE＝∠GCF，GC＝GC，‎ ‎∴△ECG≌△FCG．…………………………5分 ‎∴GE＝GF ‎∴GE＝DF＋GD＝BE＋GD． ……………6分 ‎（3）解：如图3，过C作CG⊥AD，交AD延长线于G．‎ 在直角梯形ABCD中，‎ B C A D ‎ E ‎ G ‎（第23题答案图3）‎ B C A D ‎ E ‎ G ‎∵AD∥BC，∴∠A＝∠B＝90°，‎ 又∠CGA＝90°，AB＝BC，‎ ‎∴四边形ABCD 为正方形． ‎ ‎∴AG＝BC．…………………………7分 已知∠DCE＝45°，‎ 根据（1）（2）可知，ED＝BE＋DG．……8分 ‎ 所以10=4+DG，即DG=6.‎ ‎（第23题答案图3）‎ 设AB＝x，则AE＝x－4，AD＝x－6‎ 在Rt△AED中， ∵，即．‎ 解这个方程，得：x＝12，或x＝－2（舍去）．…………………………9分 ‎∴AB＝12． ‎ 所以梯形ABCD的面积为S=‎ 答：梯形ABCD的面积为108. …………………………10分 ‎24．解：（1）由于抛物线经过A（2，0），‎ 所以，‎ 解得.…………………………1分 所以抛物线的解析式为. （*）‎ 将（*）配方，得，‎ 所以顶点P的坐标为（4，-2）…………………………2分 令y=0，得，‎ 解得. 所以点B的坐标是（6，0）. ………………3分 ‎（2）在直线 y=x上存在点D，使四边形OPBD为平行四边形. ……4分 理由如下：‎ 设直线PB的解析式为+b，把B（6,0）,P(4,-2)分别代入，得 解得 ‎ 所以直线PB的解析式为.…………………………5分 ‎ 又直线OD的解析式为 ‎ 所以直线PB∥OD. …………………………6分 ‎ 设设直线OP的解析式为，把P(4,-2)代入，得 ‎ 解得.如果OP∥BD，那么四边形OPBD为平行四边形.…………7分 A P B x y O 第24题答案图 C M D 设直线BD的解析式为，将B(6,0)代入，得0=，所以 所以直线BD的解析式为，‎ 解方程组得 所以D点的坐标为（2,2）…………………8分 ‎ （3）符合条件的点M存在.验证如下：‎ 过点P作x轴的垂线，垂足为为C，则PC=2，AC=2，由勾股定理，可得AP=4，PB=4，又AB=4，所以△APB是等边三角形，只要作∠PAB的平分线交抛物线于M点，连接PM,BM,由于AM=AM, ∠PAM=∠BAM,AB=AP，可得△AMP≌△AMB.因此即存在这样的点M,使△AMP≌△AMB.…………………………11分