2012年河北中考数学试卷 16页

‎2012年河北省初中毕业生升学文化课考试 数　学　试　卷 本试卷分卷Ⅰ和卷Ⅱ两部分；卷Ⅰ为选择题，卷Ⅱ为非选择题．‎ 本试卷满分为120分，考试时间为120分钟． ‎ 卷Ⅰ（选择题，共30分）‎ 注意事项：1．答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡上．考试结束，监考人员将试卷和答题卡一并收回．‎ ‎2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．答在试卷上无效．‎ 一、选择题（本大题共12个小题，1~6小题，每小题2分；7~12小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．下列各数中，为负数的是（　　）‎ A．0　　　　　Ｂ．　　　　　Ｃ．　　　　　Ｄ． ‎ ‎2．计算的结果是（　　）‎ A．　　Ｂ．　　Ｃ．　　Ｄ． ‎ ‎3．图1中几何体的主视图是（　　）‎ ‎4．下列各数中，为不等式组解的是（　　）‎ A．　　　　　　 Ｂ．0 Ｃ．2　　　　　　Ｄ．4 ‎ ‎5．如图2，是的直径，是弦（不是直径），于点，则下列结论正确的是（　　）‎ A．　　Ｂ．　　Ｃ．　　Ｄ．‎ ‎6．掷一枚质地均匀的硬币10次，下列说法正确的是（　　）‎ Ａ．每2次必有1次正面向上 　　B．可能有5次正面向上 C．必有5次正面向上 　　D．不可能有10次正面向上 ‎7．如图3，点在的边上，用尺规作出了，作图痕迹中，是（　　）‎ A．以点为圆心，为半径的弧　　Ｂ．以点为圆心，为半径弧 Ｃ．以点为圆心，为半径的弧　　Ｄ．以点为圆心，为半径的 ‎8．用配方法解方程，配方后的方程是（　　）‎ A．　　Ｂ．‎ Ｃ．　　Ｄ．‎ ‎9．如图4，在中，将折叠，使点分别落在点、处（点都在所在的直线上），折痕为，则等于（　　）‎ A．　　Ｂ．　　Ｃ．　　Ｄ．‎ ‎10．化简的结果是（　　）‎ A．　　Ｂ．　　Ｃ．　　Ｄ．‎ ‎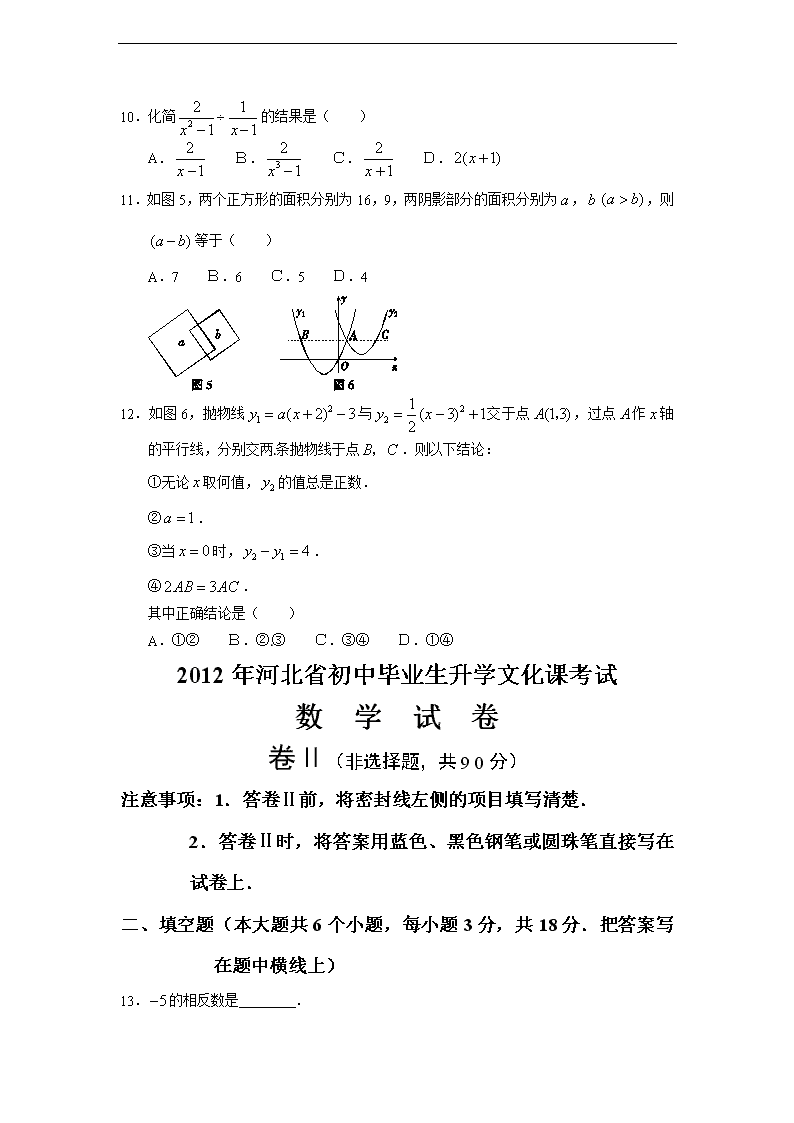11．如图5，两个正方形的面积分别为16，9，两阴影部分的面积分别为，，则等于（　　）‎ A．7　　Ｂ．6　　Ｃ．5　　Ｄ．4‎ ‎12．如图6，抛物线与交于点，过点作轴的平行线，分别交两条抛物线于点．则以下结论：[来源:Zxxk.Com]‎ ‎①无论取何值，的值总是正数．‎ ‎②．‎ ‎③当时，．‎ ‎④．‎ 其中正确结论是（　　）‎ A．①②　　Ｂ．②③　　Ｃ．③④　　Ｄ．①④‎ ‎2012年河北省初中毕业生升学文化课考试 数　学　试　卷 卷Ⅱ（非选择题，共9 0分）‎ 注意事项：1．答卷Ⅱ前，将密封线左侧的项目填写清楚． ‎ ‎2．答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上．‎ 二、填空题（本大题共6个小题，每小题3分，共18分．把答案写在题中横线上）‎ ‎13．的相反数是　　　　．‎ ‎14．如图7，相交于点，于点，若，则等于　　　．‎ ‎15．已知，则的值为　　　　．‎ ‎16．在的正方形网格格点上放三枚棋子，按图8所示的位置已放置了两枚棋子，若第三枚棋子随机放在其他格点上，则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为　　　　．‎ ‎17．某数学活动小组的20位同学站成一列做报数游戏，规则是：从前面第一位同学开始，每位同学依次报自己顺序数的倒数加1，第1位同学报，第2位同学报，第3位同学报……这样得到的20个数的积为　　　　．‎ ‎18．用4个全等的正八边形进行拼接，使相邻的两个正八边形有一条公共边，围成一圈后中间形成一个正方形，如图，用个全等的正六边形按这种方式拼接，如图，若围成一圈后中间也形成一个正多边形，则的值为　　　　． ‎ 三、解答题（本大题共8个小题，共72分．解答应写出文字说明、证明过程或演算步骤）‎ ‎19．（本小题满分8分）‎ 计算：．‎ ‎20．（本小题满分8分）‎ 如图10，某市两地之间有两条公路，一条是市区公路，另一条是外环公路.这两条公路转成等腰梯形，其中 ‎.‎ （1） 求外环公路总长和市区公路长的比；‎ （2） 某人驾车从地出发，沿市区公路去地，平均速度是40km/h，返回时沿外环公路行驶，平均速度是80km/h，结果比去时少用了h，求市区公路的长.‎ ‎21．（本小题满分8分）‎ 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小宇根据他们的成绩绘制了如下尚不完整的统计图表，并计算了甲成绩的平均数和方差（见小宇的作业）．‎ ‎（1）___________,=__________；‎ ‎（2）请完成图11中表示乙成绩变化情况的折线；‎ ‎（3）①观察图11，可看出______的成绩比较稳定（填“甲”或“乙”）.参照小宇的计算方法，计算乙成绩的方差，并验证你的判断.‎ ‎②请你从平均数和方差的角度分析，谁将被选中．‎ ‎[来源:学科网]‎ ‎22．（本小题满分8分）‎ 如图12，四边形是平行四边形，点．反比例函数的图象经过点，点是一次函数的图象与该反比例函数图象的一个公共点.‎ ‎（1）求反比例函数的解析式；‎ ‎（2）通过计算，说明一次函数的图象一定过点；‎ ‎（3）对于一次函数，当的增大而增大时，确定点横坐标的取值范围（不必写出过程）.‎ ‎23．（本小题满分9分）‎ 如图，点是线段的中点，分别以为直角顶点的均是等腰直角三角形，且在的同侧．‎ ‎（1）的数量关系为___________，‎ 的位置关系为___________；‎ ‎（2）在图中，以点为位似中心，作与位似，点是所在直线上的一点，连接，分别得到了图和图；‎ ‎　　 ①在图中，点在上，的相似比是，是的中点.求证：‎ ‎②在图中，点在的延长线上，的相似比是，若，请直接写出的长为多少时，恰好使得（用含的代数式表示）．‎ ‎24．（本小题满分9分）‎ 某工厂生产一种合金薄板（其厚度忽略不计），这些薄板的形状均为正方形，边长（单位：cm）在5~50之间，每张薄板的成本价（单位：元）与它的面积（单位：‎ ‎）成正比例，每张薄板的出厂价（单位：元）由基础价和浮动价两部分组成，其中基础价与薄板的大小无关，是固定不变的，浮动价与薄板的边长成正比例，在营销过程中得到了表格中的数据．‎ （1） 求一张薄板的出厂价与边长之间满足的函数关系式；‎ （2） 已知出厂一张边长为40cm的薄板，获得的利润是26元（利润=出厂价-成本价）.‎ ① 求一张薄板的利润与边长之间满足的函数关系式；‎ ② 当边长为多少时，出厂一张薄板获得的利润最大？最大利润是多少？‎ 参考公式：抛物线的顶点坐标是.‎ ‎25．（本小题满分10分）‎ 如图14，点在轴的正半轴上，，，‎ ‎.点从点出发，沿轴向左以每秒1个单位长的速度运动，运动时间为秒.‎ （1） 求点的坐标；‎ （2） 当时，求的值；‎ （3） 以点为圆心，为半径的随点的运动而变化，当与四边形的边（或边所在的直线）相切时，求的值． ‎ ‎[来源:学§科§网]‎ ‎26．（本小题满分12分）‎ 如图和图，在中，‎ 探究 在如图，于点，则_______，_______， 的面积=___________．‎ 拓展 如图，点在上（可与点重合），分别过点作直线的垂线，垂足为.设（当点与点重合时，我们认为=0.‎ ‎（1）用含或的代数式表示及；‎ ‎（2）求与的函数关系式，并求的最大值和最小值．‎ ‎（3）对给定的一个值，有时只能确定唯一的点，指出这样的的取值范围.‎ 发现 请你确定一条直线，使得三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.‎ ‎2012年河北省初中毕业生升学文化课考试 数学试题参考答案 一、选择题（1~6小题，每小题2分；7~12小题，每小题3发，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C A C D B D A B C A D 二、填空题（每小题3分，满分18分）‎ ‎13．5　　14．52　　15．1　　16．　　17．21　　18．6‎ 三、解答题（本大题共8小题，共72分）‎ ‎19．解：‎ ‎ = 5分 ‎ =4． 8分 ‎20．解：（1）设km，则km，km．‎ 四边形是等腰梯形，，‎ 外环公路总长和市区公路长的比为. 3分 ‎（2）由（1）可知，市区公路物长为km，外环公路的总长为km．‎ 由题意，得. 6分 解这个方程，得.‎ ‎.‎ 答：市区公路的长为10km. 8分 ‎21．解：（1）4，6 2分[来源:学科网]‎ ‎（2）如图1 3分 ‎（3）①乙 4分 ‎=1.6. 5分 由于，所以上述判断正确. 6分 ‎②因为两人成绩的平均水平（平均数）相同，乙的成绩比甲稳定，所以乙将被选中. 8分 ‎22．解：（1）由题意，，故点的坐标为（1，2）. 2分 ‎ 反比例函数的图象经过点，‎ 反比例函数的解析式为 4分 ‎（2）当时，‎ 一次函数的图象一定过点． 6分 ‎（3）设点的横坐标为 8分 ‎（注：对（3）中的取值范围，其他正确写法，均相应给分）‎ ‎23．解：（1）． 2分 ‎（2）①证明：由题意，‎ 位似且相似比是，‎ ‎.‎ ‎. 5分 又.‎ ‎. 7分 ‎②的长为. 9分 ‎24．解：（1）设一张薄板的边长为cm，它的出厂价为元，基础价为元，浮动价为元，则. 2分 由表格中的数据，得 解得 所以 4分 ‎（2）①设一张薄板的利润为元，它的成本价为元，由题意，得 ‎ 5分 将代入中，得.‎ 解得 所以 7分 ‎②因为，所以，当（在5~50之间）时，‎ 即出厂一张边长为25cm的薄板，获得的利润最大，最大利润是35元. 9分 ‎（注：边长的取值范围不作为扣分点）‎ ‎25．解：（1），‎ 又点在轴的正半轴上， ‎ 点的坐标为（0，3） 2分 ‎（2）当点在点右侧时，如图2.‎ 若，得.‎ 故，此时. 4分 当点在点左侧时，如图3，由，‎ 得，故.‎ 此时.‎ 的值为或 6分 ‎（3）由题意知，若与四边形的边相切，有以下三种情况：‎ ‎①当与相切于点时，有，从而得到.‎ 此时. 7分 ‎②当与相切于点时，有，即点与点重合，‎ 此时. 8分 ‎③当与相切时，由题意，，‎ 点为切点，如图4..‎ 于是.解处.‎ 的值为1或4或5.6. 10分 ‎26．解：探究：12，15，84 3分 拓展：（1）由三角形面积公式，得. 4分 ‎（2）由（1）得，‎ ‎. 5分 由于边上的高为，‎ 的取值范围是.‎ 随的增大而减小，‎ 当时，的最大值为15. 7分 当时，的最小值为12. 8分 ‎（3）的取值范围是或. 10分 发现：所在的直线， 11分 最小值为. 12分