中考数学压轴题(精选全集)+中考数学试题及答案解析等精品复习资料大全，精品资料 138页

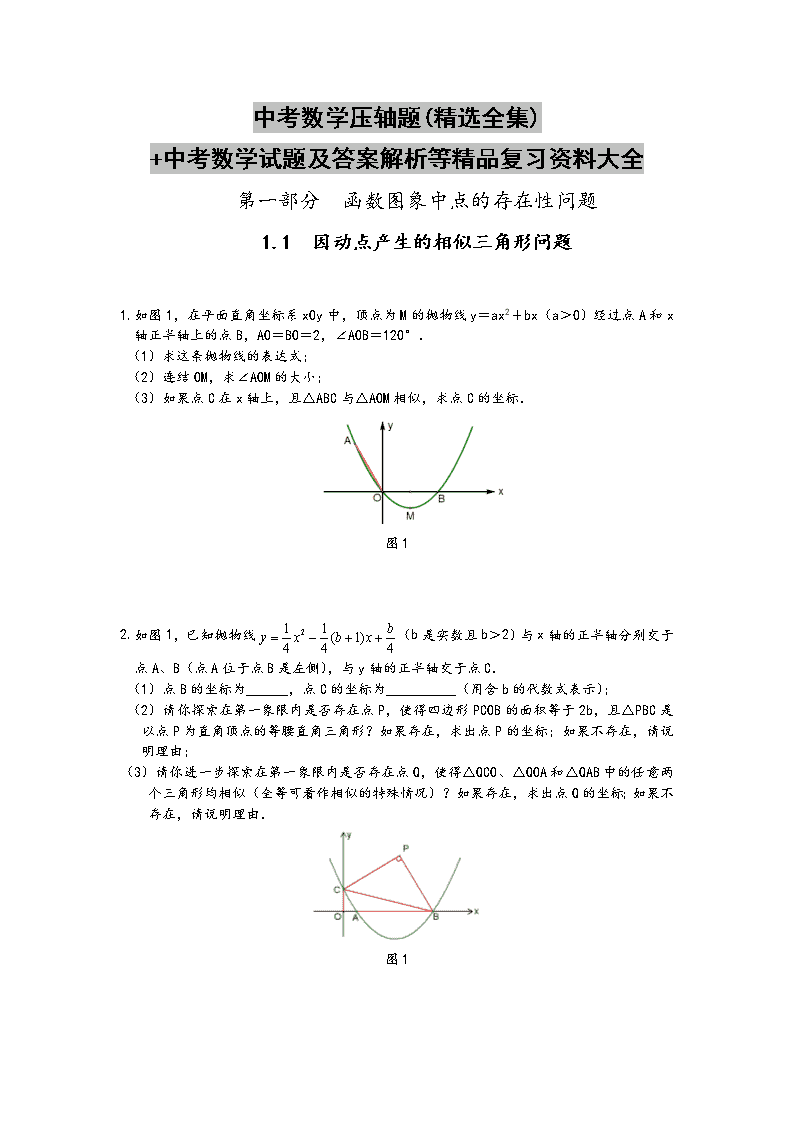
中考数学压轴题(精选全集) +中考数学试题及答案解析等精品复习资料大全 第一部分 函数图象中点的存在性问题 1.1 因动点产生的相似三角形问题 1.如图 1，在平面直角坐标系 xOy 中，顶点为 M 的抛物线 y＝ax2＋bx（a＞0）经过点 A 和 x 轴 正半轴上的点 B，AO＝BO＝2，∠AOB＝120°． （1）求这条抛物线的表达式； （2）连结 OM，求∠AOM 的大小； （3）如果点 C 在 x 轴上，且△ABC 与△AOM 相似，求点 C 的坐标． 图 1 2.如图 1，已知抛物线 21 1 ( 1)4 4 4 by x b x    （b 是实数且 b＞2）与 x 轴的正半轴分别交于 点 A、B（点 A 位于点 B 是左侧），与 y 轴的正半轴交于点 C． （1）点 B 的坐标为______，点 C 的坐标为__________（用含 b 的代数式表示）； （2）请你探索在第一象限内是否存在点 P，使得四边形 PCOB 的面积等于 2b，且△PBC 是 以点 P 为直角顶点的等腰直角三角形？如果存在，求出点 P 的坐标；如果不存在，请说 明 理由； （3）请你进一步探索在第一象限内是否存在点 Q，使得△QCO、△QOA 和△QAB 中的任意两 个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点 Q 的坐标；如果不 存在，请说明理由． 图 1 3.如图 1，已知抛物线的方程 C1： 1 ( 2)( )y x x mm     (m＞0)与 x 轴交于点 B、C，与 y 轴交于点 E，且点 B 在点 C 的左侧． （1）若抛物线 C1 过点 M(2, 2)，求实数 m 的值； （2）在（1）的条件下，求△BCE 的面积； （3）在（1）的条件下，在抛物线的对称轴上找一点 H，使得 BH＋EH 最小，求出点 H 的坐 标； （4）在第四象限内，抛物线 C1 上是否存在点 F，使得以点 B、C、F 为顶点的三角形与△BCE 相似？若存在，求 m 的值；若不存在，请说明理由． 图 1 4.如图 1，已知梯形 OABC，抛物线分别过点 O（0，0）、A（2，0）、B（6，3）． （1）直接写出抛物线的对称轴、解析式及顶点 M 的坐标； （2）将图 1 中梯形 OABC 的上下底边所在的直线 OA、CB 以相同的速度同时向上平移，分别 交抛物线于点 O1、A1、C1、B1，得到如图 2 的梯形 O1A1B1C1．设梯形 O1A1B1C1 的面积为 S，A1、 B1 的坐标分别为 (x1，y1)、(x2，y2)．用含 S 的代数式表示 x2－x1，并求出当 S=36 时点 A1 的坐 标； （3）在图 1 中，设点 D 的坐标为(1，3)，动点 P 从点 B 出发，以每秒 1 个单位长度的 速度沿着线段 BC 运动，动点 Q 从点 D 出发，以与点 P 相同的速度沿着线段 DM 运动．P、Q 两点同时出发，当点 Q 到达点 M 时，P、Q 两点同时停止运动．设 P、Q 两点的运动时间为 t， 是否存在某一时刻 t，使得直线 PQ、直线 AB、x 轴围成的三角形与直线 PQ、直线 AB、抛物 线的对称轴围成的三角形相似？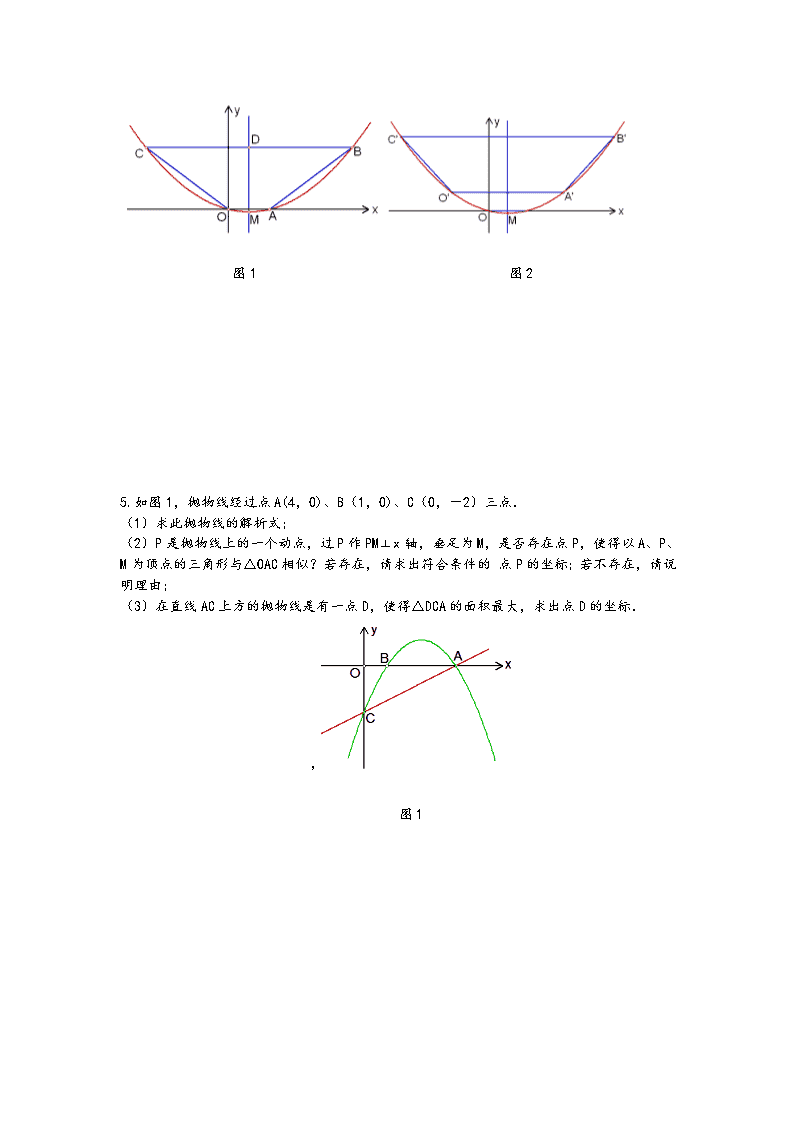若存在，请求出 t 的值；若不存在，请说明理由． 图 1 图 2 5.如图 1，抛物线经过点 A(4，0)、B（1，0)、C（0，－2）三点． （1）求此抛物线的解析式； （2）P 是抛物线上的一个动点，过 P 作 PM⊥x 轴，垂足为 M，是否存在点 P，使得以 A、P、 M 为顶点的三角形与△OAC 相似？若存在，请求出符合条件的 点 P 的坐标；若不存在，请说 明理由； （3）在直线 AC 上方的抛物线是有一点 D，使得△DCA 的面积最大，求出点 D 的坐标． , 图 1 1.2 因动点产生的等腰三角形问题 6.如图 1，在 Rt△ABC 中，∠A＝90°，AB＝6，AC＝8，点 D 为边 BC 的中点，DE⊥BC 交边 AC 于点 E，点 P 为射线 AB 上的一动点，点 Q 为边 AC 上的一动点，且∠PDQ＝90 （1）求 ED、EC 的长； （2）若 BP＝2，求 CQ 的长； （3）记线段 PQ 与线段 DE 的交点为 F，若△PDF 为等腰三角形，求 BP 的长． 图 1 备用图 7.如图 1，抛物线 y＝ax2＋bx＋c 经过 A(－1,0)、B(3, 0)、C(0 ,3)三点，直线 l 是抛物线 的对称轴． （1）求抛物线的函数关系式； （2）设点 P 是直线 l 上的一个动点，当△PAC 的周长最小时，求点 P 的坐标； （3）在直线 l 上是否存在点 M，使△MAC 为等腰三角形，若存在，直接写出所有符合条件的 点 M 的坐标；若不存在，请说明理由． 图 1 8.如图 1，点 A 在 x 轴上，OA＝4，将线段 OA 绕点 O 顺时针旋转 120°至 OB 的位置． （1）求点 B 的坐标； （2）求经过 A、O、B 的抛物线的解析式； （3）在此抛物线的对称轴上，是否存在点 P，使得以点 P、O、B 为顶点的三角形是等腰三 角形？若存在，求点 P 的坐标；若不存在，请说明理由． 图 1 9.如图 1，已知一次函数 y＝－x＋7 与正比例函数 4 3y x 的图象交于点 A，且与 x 轴交于点 B． （1）求点 A 和点 B 的坐标； （2）过点 A 作 AC⊥y 轴于点 C，过点 B 作直线 l//y 轴．动点 P 从点 O 出发，以每秒 1 个单 位长的速度，沿 O—C—A 的路线向点 A 运动；同时直线 l 从点 B 出发，以相同速度向左平 移，在平移过程中，直线 l 交 x 轴于点 R，交线段 BA 或线段 AO 于点 Q．当点 P 到达点 A 时，点 P 和直线 l 都停止运动．在运动过程中，设动点 P 运动的时间为 t 秒． ①当 t 为何值时，以 A、P、R 为顶点的三角形的面积为 8？ ②是否存在以 A、P、Q 为顶点的三角形是等腰三角形？若存在，求 t 的值；若不存在，请 说明理由． 10.如图 1，在矩形 ABCD 中，AB＝m（m 是大于 0 的常数），BC＝8，E 为线段 BC 上的动点（不 与 B、C 重合）．连结 DE，作 EF⊥DE，EF 与射线 BA 交于点 F，设 CE＝x，BF＝y． （1）求 y 关于 x 的函数关系式； （2）若 m＝8，求 x 为何值时，y 的值最大，最大值是多少？ （3）若 12y m  ，要使△DEF 为等腰三角形，m 的值应为多少？ 图 1 11.如图 1，在等腰梯形 ABCD 中，AD//BC，E 是 AB 的中点，过点 E 作 EF//BC 交 CD 于点 F， AB＝4，BC＝6，∠B＝60°． （1）求点 E 到 BC 的距离； （2）点 P 为线段 EF 上的一个动点，过点 P 作 PM⊥EF 交 BC 于 M，过 M 作 MN//AB 交折 线 ADC 于 N，连结 PN，设 EP＝x． ①当点 N 在线段 AD 上时（如图 2），△PMN 的形状是否发生改变？若不变，求出△PMN 的周长；若改变，请说明理由； ②当点 N 在线段 DC 上时（如图 3），是否存在点 P，使△PMN 为等腰三角形？若存在， 请求出所有满足条件的 x 的值；若不存在，请说明理由． 图 1 图 2 图 3 1.3 因动点产生的直角三角形问题 12.如图 1，抛物线 21 3 44 2y x x   与 x 轴交于 A、B 两点（点 B 在点 A 的右侧），与 y 轴交 于点 C，连结 BC，以 BC 为一边，点 O 为对称中心作菱形 BDEC，点 P 是 x 轴上的一个动点， 设点 P 的坐标为(m, 0)，过点 P 作 x 轴的垂线 l 交抛物线于点 Q． （1）求点 A、B、C 的坐标； （2）当点 P 在线段 OB 上运动时，直线 l 分别交 BD、BC 于点 M、N．试探究 m 为何值时， 四边形 CQMD 是平行四边形，此时，请判断四边形 CQBM 的形状，并说明理由； （3）当点 P 在线段 EB 上运动时，是否存在点 Q，使△BDQ 为直角三角形，若存在，请 直接写出点 Q 的坐标；若不存在，请说明理由． 图 1 13.如图 1，抛物线 23 3 38 4y x x    与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴 交于点 C． （1）求点 A、B 的坐标； （2）设 D 为已知抛物线的对称轴上的任意一点，当△ACD 的面积等于△ACB 的面积时， 求点 D 的坐标； （3）若直线 l 过点 E(4, 0)，M 为直线 l 上的动点，当以 A、B、M 为顶点所作的直角三 角形有且只有．．．．三个时，求直线 l 的解析式． 图 1 14.平面直角坐标系中，反比例函数与二次函数 y＝k(x2＋x－1)的图象交于点 A(1,k)和点 B(－1,－k)． （1）当 k＝－2 时，求反比例函数的解析式； （2）要使反比例函数与二次函数都是 y 随 x 增大而增大，求 k 应满足的条件以及 x 的 取值范围； （3）设二次函数的图象的顶点为 Q，当△ABQ 是以 AB 为斜边的直角三角形时，求 k 的 值． 16.直角坐标系 xOy 中，抛物线 2 21 5 3 24 4 m my x x m m      与 x 轴的交点分别为原 点 O 和点 A，点 B(2,n)在这条抛物线上． （1）求点 B 的坐标； （2）点 P 在线段 OA 上，从点 O 出发向点 A 运动，过点 P 作 x 轴的垂线，与直线 OB 交于点 E，延长 PE 到点 D，使得 ED＝PE，以 PD 为斜边，在 PD 右侧作等腰直角三角形 PCD（当点 P 运动时，点 C、D 也随之运动）． ①当等腰直角三角形 PCD 的顶点 C 落在此抛物线上时，求 OP 的长； ②若点 P 从点 O 出发向点 A 作匀速运动，速度为每秒 1 个单位，同时线段 OA 上另一个点 Q 从点 A 出发向点 O 作匀速运动，速度为每秒 2 个单位（当点 Q 到达点 O 时停止运动，点 P 也停止运动）．过 Q 作 x 轴的垂线，与直线 AB 交于点 F，延长 QF 到点 M，使得 FM＝QF，以 QM 为斜边，在 QM 的左侧作等腰直角三角形 QMN（当点 Q 运动时，点 M、N 也随之运动）．若 点 P 运动到 t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，求此刻 t 的值． 图 1 17.已知 A、B 是线段 MN 上的两点， 4MN ， 1MA ， 1MB ．以 A 为中心顺时针旋转点 M， 以 B 为中心逆时针旋转点 N，使 M、N 两点重合成一点 C，构成△ABC，设 xAB  ． （1）求 x 的取值范围； （2）若△ABC 为直角三角形，求 x 的值； （3）探究：△ABC 的最大面积？ 图 1 18.直线 43 4  xy 和 x 轴、y 轴的交点分别为 B、C，点 A 的坐标是（-2，0）． （1）试说明△ABC 是等腰三角形； （2）动点 M 从 A 出发沿 x 轴向点 B 运动，同时动点 N 从点 B 出发沿线段 BC 向点 C 运动，运 动的速度均为每秒 1 个单位长度．当其中一个动点到达终点时，他们都停止运动．设 M 运动 t 秒时，△MON 的面积为 S． ① 求 S 与 t 的函数关系式； ② 设点 M 在线段 OB 上运动时，是否存在 S＝4 的情形？若存在，求出对应的 t 值；若不存 在请说明理由； ③在运动过程中，当△MON 为直角三角形时，求 t 的值． 图 1 19.直线 43 4  xy 和 x 轴、y 轴的交点分别为 B、C，点 A 的坐标是（-2，0）． （1）试说明△ABC 是等腰三角形； （2）动点 M 从 A 出发沿 x 轴向点 B 运动，同时动点 N 从点 B 出发沿线段 BC 向点 C 运动，运 动的速度均为每秒 1 个单位长度．当其中一个动点到达终点时，他们都停止运动．设 M 运动 t 秒时，△MON 的面积为 S． ① 求 S 与 t 的函数关系式； ② 设点 M 在线段 OB 上运动时，是否存在 S＝4 的情形？若存在，求出对应的 t 值；若不存 在请说明理由； ③在运动过程中，当△MON 为直角三角形时，求 t 的值． 图 1 20.知抛物线 y＝－x2＋bx＋c 经过 A(0, 1)、B(4, 3)两点． （1）求抛物线的解析式； （2）求 tan∠ABO 的值； （3）过点 B 作 BC⊥x 轴，垂足为 C，在对称轴的左侧且平行于 y 轴的直线交线段 AB 于点 N， 交抛物线于点 M，若四边形 MNCB 为平行四边形，求点 M 的坐标． 图 1 21.Rt△ABC 中，∠C＝90°，AC＝6，BC＝8，动点 P 从点 A 开始沿边 AC 向点 C 以每秒 1 个 单位长度的速度运动，动点 Q 从点 C 开始沿边 CB 向点 B 以每秒 2 个单位长度的速度运动， 过点 P 作 PD//BC，交 AB 于点 D，联结 PQ．点 P、Q 分别从点 A、C 同时出发，当其中一点到 达端点时，另一点也随之停止运动，设运动的时间为 t 秒（t≥0）． （1）直接用含 t 的代数式分别表示：QB＝_______，PD＝_______； （2）是否存在 t 的值，使四边形 PDBQ 为菱形？若存在，求出 t 的值；若不存在，说明理由， 并探究如何改变点 Q 的速度（匀速运动），使四边形 PDBQ 在某一时刻为菱形，求点 Q 的速度； （3）如图 2，在整个运动过程中，求出线段 PQ 的中点 M 所经过的路径长． 图 1 图 2 22.平面直角坐标系中，已知矩形 ABCD 的三个顶点 B(1, 0)、C(3, 0)、D(3, 4)．以 A 为顶 点的抛物线 y＝ax2＋bx＋c 过点 C．动点 P 从点 A 出发，沿线段 AB 向点 B 运动，同时动点 Q 从点 C 出发，沿线段 CD 向点 D 运动．点 P、Q 的运动速度均为每秒 1 个单位，运动时间为 t 秒．过点 P 作 PE⊥AB 交 AC 于点 E． （1）直接写出点 A 的坐标，并求出抛物线的解析式； （2）过点 E 作 EF⊥AD 于 F，交抛物线于点 G，当 t 为何值时，△ACG 的面积最大？最大值 为多少？ （3）在动点 P、Q 运动的过程中，当 t 为何值时，在矩形 ABCD 内（包括边界）存在点 H， 使以 C、Q、E、H 为顶点的四边形为菱形？请直接写出 t 的值． 图 1 23.物线 c1： 23 3y x   沿 x 轴翻折，得到抛物线 c2，如图 1 所示． （1）请直接写出抛物线 c2 的表达式； （2）现将抛物线 c1 向左平移 m 个单位长度，平移后得到新抛物线的顶点为 M，与 x 轴的交 点从左到右依次为 A、B；将抛物线 c2 向右也平移 m 个单位长度，平移后得到新抛物线的顶 点为 N，与 x 轴的交点从左到右依次为 D、E． ①当 B、D 是线段 AE 的三等分点时，求 m 的值； ②在平移过程中，是否存在以点 A、N、E、M 为顶点的四边形是矩形的情形？若存在，请求 出此时 m 的值；若不存在，请说明理由． 图 1 24 角梯形 OABC 中，CB//OA，∠COA＝90°，CB＝3，OA＝6，BA＝3 5 ．分别以 OA、OC 边所 在直线为 x 轴、y 轴建立如图 1 所示的平面直角坐标系． （1）求点 B 的坐标； （2）已知 D、E 分别为线段 OC、OB 上的点，OD＝5，OE＝2EB，直线 DE 交 x 轴于点 F．求直 线 DE 的解析式； （3）点 M 是（2）中直线 DE 上的一个动点，在 x 轴上方的平面内是否存在另一点 N，使以 O、 D、M、N 为顶点的四边形是菱形？若存在，请求出点 N 的坐标；若不存在，请说明理由． 图 1 图 2 25.物线 322  xxy 与 x 轴相交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴相交于点 C，顶点为 D． （1）直接写出 A、B、C 三点的坐标和抛物线的对称轴； （2）连结 BC，与抛物线的对称轴交于点 E，点 P 为线段 BC 上的一个动点，过点 P 作 PF//DE 交抛物线于点 F，设点 P 的横坐标为 m． ①用含 m 的代数式表示线段 PF 的长，并求出当 m 为何值时，四边形 PEDF 为平行四边形？ ②设△BCF 的面积为 S，求 S 与 m 的函数关系． 图 1 26 直线 y＝3x－3 分别与 x 轴、y 轴交于点 A，B，抛物线 y＝ax2＋2x＋c 经过点 A，B． （1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐 标； （2）记该抛物线的对称轴为直线 l，点 B 关于直线 l 的对称点 为 C，若点 D 在 y 轴的正半轴上，且四边形 ABCD 为梯形． ①求点 D 的坐标； ②将此抛物线向右平移，平移后抛物线的顶点为 P，其对称轴与 直线 y＝3x－3 交于点 E，若 7 3tan DPE ，求四边形 BDEP 的 面积． 图 1 27.，把两个全等的 Rt△AOB 和 Rt△COD 方别置于平面直角坐标系中，使直角边 OB、OD 在 x 轴上．已知点 A(1，2)，过 A、C 两点的直线分别交 x 轴、y 轴于点 E、F．抛物线 y＝ax2＋ bx＋c 经过 O、A、C 三点． （1）求该抛物线的函数解析式； （2）点 P 为线段 OC 上的一个动点，过点 P 作 y 轴的平行线交抛物线于点 M，交 x 轴于点 N， 问是否存在这样的点 P，使得四边形 ABPM 为等腰梯形？若存在，求出此时点 P 的坐标；若 不存在，请说明理由； （3）若△AOB 沿 AC 方向平移（点 A 始终在线段 AC 上，且不与点 C 重合），△AOB 在平移的 过程中与△COD 重叠部分的面积记为 S．试探究 S 是否存在最大值？若存在，求出这个最大 值；若不存在，请说明理由． 图 1 28.次函数的图象经过 A（2，0）、C(0，12) 两点，且对称轴为直线 x＝4，设顶点为点 P， 与 x 轴的另一交点为点 B． （1）求二次函数的解析式及顶点 P 的坐标； （2）如图 1，在直线 y＝2x 上是否存在点 D，使四边形 OPBD 为等腰梯形？若存在，求 出点 D 的坐标；若不存在，请说明理由； （3）如图 2，点 M 是线段 OP 上的一个动点（O、P 两点除外），以每秒 2 个单位长度的 速度由点 P 向点 O 运动，过点 M 作直线 MN//x 轴，交 PB 于点 N． 将△PMN 沿直线 MN 对折， 得到△P1MN． 在动点 M 的运动过程中，设△P1MN 与梯形 OMNB 的重叠部分的面积为 S，运动 时间为 t 秒，求 S 关于 t 的函数关系式． 图 1 图 2 29.在平面直角坐标系 xOy 中，抛物线的解析式是 y ＝ 21 14 x  ，点 C 的坐标为(–4，0)， 平行四边形 OABC 的顶点 A，B 在抛物线上，AB 与 y 轴交于点 M，已知点 Q(x，y)在抛物线上， 点 P(t，0)在 x 轴上． (1) 写出点 M 的坐标； (2) 当四边形 CMQP 是以 MQ，PC 为腰的梯形时． ① 求 t 关于 x 的函数解析式和自变量 x 的取值范围； ② 当梯形 CMQP 的两底的长度之比为 1∶2 时，求 t 的值． 30 图 1，二次函数 )0(2  pqpxxy 的图象与 x 轴交于 A、B 两点，与 y 轴交于点 C （0，－1），△ABC 的面积为 4 5 ． （1）求该二次函数的关系式； （2）过 y 轴上的一点 M（0，m）作 y 轴的垂线，若该垂线与△ABC 的外接圆有公共点，求 m 的取值范围； （3）在该二次函数的图象上是否存在点 D，使以 A、B、C、D 为顶点的四边形为直角梯形？ 若存在，求出点 D 的坐标；若不存在，请说明理由． 图 1 1.6 因动点产生的面积问题 31.知抛物线 21 2y x bx c   （b、c 是常数，且 c＜0）与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴的负半轴交于点 C，点 A 的坐标为(－1,0)． （1）b＝______，点 B 的横坐标为_______（上述结果均用含 c 的代数式表示）； （2）连结 BC，过点 A 作直线 AE//BC，与抛物线交于点 E．点 D 是 x 轴上一点，坐标为(2,0)， 当 C、D、E 三点在同一直线上时，求抛物线的解析式； （3）在（2）的条件下，点 P 是 x 轴下方的抛物线上的一动点，连结 PB、PC．设△PBC 的面 积为 S． ①求 S 的取值范围； ②若△PBC 的面积 S 为正整数，则这样的△PBC 共有_____个． 图 1 32.平面直角坐标系中放置一直角三角板，其顶点为 A(0, 1)、B(2, 0)、O(0, 0)，将此三 角板绕原点 O 逆时针旋转 90°，得到三角形 A′B′O． （1）一抛物线经过点 A′、B′、B，求该抛物线的解析式； （2）设点 P 是第一象限内抛物线上的一个动点，是否存在点 P，使四边形 PB′A′B 的面积 是△A′B′O 面积的 4 倍？若存在，请求出点 P 的坐标；若不存在，请说明理由； （3）在（2）的条件下，试指出四边形 PB′A′B 是哪种形状的四边形？并写出它的两条性 质． 图 1 33..面直角坐标系中，直线 1 12y x  与抛物线 y＝ax2＋bx－3 交于 A、B 两点，点 A 在 x 轴 上，点 B 的纵坐标为 3．点 P 是直线 AB 下方的抛物线上的一动点（不与点 A、B 重合），过 点 P 作 x 轴的垂线交直线 AB 于点 C，作 PD⊥AB 于点 D． （1）求 a、b 及 sin∠ACP 的值； （2）设点 P 的横坐标为 m． ①用含 m 的代数式表示线段 PD 的长，并求出线段 PD 长的最大值； ②连结 PB，线段 PC 把△PDB 分成两个三角形，是否存在适合的 m 的值，使这两个三角形的 面积比为 9∶10？若存在，直接写出 m 的值；若不存在，请说明理由． 图 1 34.直线 l 经过点 A(1，0)，且与双曲线 my x  (x＞0)交于点 B(2，1)．过点 ( , 1)P p p  (p＞1) 作 x 轴的平行线分别交曲线 my x  (x＞0)和 my x   (x＜0)于 M、N 两点． （1）求 m 的值及直线 l 的解析式； （2）若点 P 在直线 y＝2 上，求证：△PMB∽△PNA； （3）是否存在实数 p，使得 S△AMN＝4S△AMP？若存在，请求出所有满足条件的 p 的值；若不存 在，请说明理由． 图 1 35.边形 OABC 是矩形，点 A、C 的坐标分别为(3,0)，(0,1)．点 D 是线段 BC 上的动点（与端 点 B、C 不重合），过点 D 作直线 1 2y x b   交折线 OAB 于点 E． （1）记△ODE 的面积为 S，求 S 与 b 的函数关系式； （2）当点 E 在线段 OA 上时，若矩形 OABC 关于直线 DE 的对称图形为四边形 O1A1B1C1，试探 究四边形 O1A1B1C1 与矩形 OABC 的重叠部分的面积是否发生变化？若不变，求出重叠部分的面 积；若改变，请说明理由． 图 1 36.△ABC 中，∠C＝90°，AC＝3，BC＝4，CD 是斜边 AB 上的高，点 E 在斜边 AB 上，过点 E 作直线与△ABC 的直角边相交于点 F，设 AE＝x，△AEF 的面积为 y． （1）求线段 AD 的长； （2）若 EF⊥AB，当点 E 在斜边 AB 上移动时， ①求 y 与 x 的函数关系式（写出自变量 x 的取值范围）； ②当 x 取何值时，y 有最大值？并求出最大值． （3）若点 F 在直角边 AC 上（点 F 与 A、C 不重合），点 E 在斜边 AB 上移动，试问，是否存 在直线 EF 将△ABC 的周长和面积同时平分？若存在直线 EF，求出 x 的值；若不存在直线 EF， 请说明理由． 图 1 备用图 1.7 因动点产生的相切问题 37.知⊙O 的半径长为 3，点 A 是⊙O 上一定点，点 P 为⊙O 上不同于点 A 的动点． （1）当 1tan 2A  时，求 AP 的长； （2）如果⊙Q 过点 P、O，且点 Q 在直线 AP 上（如图 2），设 AP＝x，QP＝y，求 y 关于 x 的 函数关系式，并写出函数的定义域； （3）在（2）的条件下，当 4tan 3A  时（如图 3），存在⊙M 与⊙O 相内切，同时与⊙Q 相外 切，且 OM⊥OQ，试求⊙M 的半径的长． 图 1 图 2 图 3 38. A(－5,0)，B(－3,0)，点 C 在 y 轴的正半轴上，∠CBO＝45°，CD//AB，∠CDA＝90．点 P 从点 Q(4,0)出发，沿 x 轴向左以每秒 1 个单位长的速度运动，运动时间为 t 秒． （1）求点 C 的坐标； （2）当∠BCP＝15°时，求 t 的值； （3）以点 P 为圆心，PC 为半径的⊙P 随点 P 的运动而 变化，当⊙P 与四边形 ABCD 的边（或边所在的直线）相切 时，求 t 的值． 图 1 39.形 ABCD 的边长为 2 厘米，∠DAB＝60°．点 P 从 A 出发，以每 秒 3 厘米的速度沿 AC 向 C 作匀速运动；与此同时，点 Q 也从点 A 出发，以每秒 1 厘米的速度沿射线作匀速运动．当点 P 到达点 C 时，P、Q 都停止运动．设点 P 运动的时间为 t 秒． （1）当 P 异于 A、C 时，请说明 PQ//BC； （2）以 P 为圆心、PQ 长为半径作圆，请问：在整个运动过程中，t 为怎样的值时，⊙P 与 边 BC 分别有 1 个公共点和 2 个公共点？ 1.8 因动点产生的线段和差问题 40 面直角坐标系中，已知点 A(－2,0)，B(0,4)，点 E 在 OB 上，且∠OAE＝∠OBA． （1）如图 1，求点 E 的坐标； （2）如图 2，将△AEO 沿 x 轴向右平移得到△AE′O′，连结 A′B、BE′． ①设 AA′＝m，其中 0＜m＜2，使用含 m 的式子表示 A′B2＋BE′2，并求出使 A′B2＋BE′2 取得最小值时点 E′的坐标； ②当 A′B＋BE′取得最小值时，求点 E′的坐标（直接写出结果即可）． 图 1 图 2 41.平面直角坐标系中，抛物线 y＝ax2＋bx＋c 经过 A(－2, －4 )、O(0, 0)、 B(2, 0)三点． （1）求抛物线 y＝ax2＋bx＋c 的解析式； （2）若点 M 是该抛物线对称轴上的一点，求 AM＋OM 的最小值． 图 1 第二部分 函数图象中点的存在性问题 2.1 由比例线段产生的函数关系问题 42.在平面直角坐标系中，O 为坐标原点，点 A 的坐标为(0,4)，点 B 的坐标为(4,0)，点 C 的坐标为(－4,0)，点 P 在射线 AB 上运动，连结 CP 与 y 轴交于点 D，连结 BD．过 P、D、B 三点作⊙Q，与 y 轴的另一个交点为 E，延长 DQ 交⊙Q 于 F，连结 EF、BF． （1）求直线 AB 的函数解析式； （2）当点 P 在线段 AB（不包括 A、B 两点）上时． ①求证：∠BDE＝∠ADP； ②设 DE＝x，DF＝y，请求出 y 关于 x 的函数解析式； （3）请你探究：点 P 在运动过程中，是否存在以 B、D、F 为顶点的直角三角形，满足两条 直角边之比为 2∶1？如果存在，求出此时点 P 的坐标；如果不存在， 请说明理由． 43.在 Rt△ABC 中，∠C＝90°，AC＝6， 5 3sin B ，⊙B 的半径长为 1，⊙B 交边 CB 于点 P， 点 O 是边 AB 上的动点． （1）如图 1，将⊙B 绕点 P 旋转 180°得到⊙M，请判断⊙M 与直线 AB 的位置关系； （2）如图 2，在（1）的条件下，当△OMP 是等腰三角形时，求 OA 的长； （3）如图 3，点 N 是边 BC 上的动点，如果以 NB 为半径的⊙N 和以 OA 为半径的⊙O 外切， 设 NB＝y，OA＝x，求 y 关于 x 的函数关系式及定义域． 图 1 图 2 图 3 44.如图 1，甲、乙两人分别从 A、B 两点同时出发，点 O 为坐标原点．甲沿 AO 方向、乙沿 BO 方向均以每小时 4 千米的速度行走，t 小时后，甲到达 M 点，乙到达 N 点． （1）请说明甲、乙两人到达点 O 前，MN 与 AB 不可能平行； （2）当 t 为何值时，△OMN∽△OBA？（3）甲、乙两人之间的距离为 MN 的长．设 s＝MN2， 求 s 与 t 之间的函数关系式，并求甲、乙两人之间距离的最小值． 2.2 由面积产生的函数关系问题 45.如图 1， △ABC 是以 BC 为底边的等腰三角形，点 A、C 分别是一次函数 3 34y x   的 图像与 y 轴、x 轴的交点，点 B 在二次函数 21 8y x bx c   的图像上，且该二次函数图像 上存在一点 D 使四边形 ABCD 能构成平行四边形． （1）试求 b、c 的值，并写出该二次函数的解析式； （2）动点 P 从 A 到 D，同时动点 Q 从 C 到 A 都以每秒 1 个单位的速度运动，问： ①当 P 运动到何处时，由 PQ⊥AC？ ②当 P 运动到何处时，四边形 PDCQ 的面积最小？此时四边形 PDCQ 的面积是多少？ 图 1 46.如图 1，抛物线 21 3 92 2y x x   与 x 轴交于 A、B 两点，与 y 轴交于点 C，联结 BC、AC． （1）求 AB 和 OC 的长； （2）点 E 从点 A 出发，沿 x 轴向点 B 运动（点 E 与点 A、B 不重合），过点 E 作 BC 的平 行线交 AC 于点 D．设 AE 的长为 m，△ADE 的面积为 s，求 s 关于 m 的函数关系式，并写出自 变量 m 的取值范围； （3）在（2）的条件下，联结 CE，求△CDE 面积的最大值；此时，求出以点 E 为圆心， 与 BC 相切的圆的面积（结果保留π）． 图 1 47.如图 1，在 Rt△ABC 中，∠C＝90°，AC＝8，BC＝6，点 P 在 AB 上，AP＝2．点 E、F 同 时从点 P 出发，分别沿 PA、PB 以每秒 1 个单位长度的速度向点 A、B 匀速运动，点 E 到达点 A 后立刻以原速度沿 AB 向点 B 运动，点 F 运动到点 B 时停止，点 E 也随之停止．在点 E、F 运动过程中，以 EF 为边作正方形 EFGH，使它与△ABC 在线段 AB 的同侧．设 E、F 运动的时 间为 t 秒(t＞0)，正方形 EFGH 与△ABC 重叠部分的面积为 S． （1）当 t＝1 时，正方形 EFGH 的边长是______；当 t＝3 时，正方形 EFGH 的边长是________； （2）当 1＜t≤2 时，求 S 与 t 的函数关系式； （3）直接答出：在整个运动过程中，当 t 为何值时，S 最大？最大面积是多少？ 图 1 48.如图 1，在平面直角坐标系中，四边形 OABC 是平行四边形．直线 l 经过 O、C 两点，点 A 的坐标为(8，0)，点 B 的坐标为(11，4)，动点 P 在线段 OA 上从 O 出发以每秒 1 个单位的速 度向点 A 运动，同时动点 Q 从点 A 出发以每秒 2 个单位的速度沿 A→B→C 的方向向点 C 运动， 过点 P 作 PM 垂直于 x 轴，与折线 O—C—B 相交于点 M．当 P、Q 两点中有一点到达终点时， 另一点也随之停止运动，设点 P、Q 运动的时间为 t 秒（t＞0），△MPQ 的面积为 S． （1）点 C 的坐标为____________，直线 l 的解析式为____________； （2）试求点 Q 与点 M 相遇前 S 与 t 的函数关系式，并写出相应的 t 的取值范围． （3）试求题（2）中当 t 为何值时，S 的值最大？最大值是多少？ 图 1 49.如图 1，矩形 ABCD 中，AB＝6，BC＝ 2 3 ，点 O 是 AB 的中点，点 P 在 AB 的延长线上， 且 BP＝3．一动点 E 从 O 点出发，以每秒 1 个单位长度的速度沿 OA 匀速运动，到达 A 点后， 立即以原速度沿 AO 返回；另一动点 F 从 P 点出发，以每秒 1 个单位长度的速度沿射线 PA 匀速运动，点 E、F 同时出发，当两点相遇时停止运动，在点 E、F 的运动过程中，以 EF 为 边作等边△EFG，使△EFG 和矩形 ABCD 在射线 PA 的同侧．设运动的时间为 t 秒（t≥0）． （1）当等边△EFG 的边 FG 恰好经过点 C 时，求运动时间 t 的值； （2）在整个运动过程中，设等边△EFG 和矩形 ABCD 重叠部分的面积为 S，请直接写出 S 与 t 之间的函数关系 式和相应的自变量 t 的取值范围； （3）设 EG 与矩形 ABCD 的对角线 AC 的交点为 H，是 否存在这样的 t，使△AOH 是等腰三角形？若存在，求出 对应的 t 的值；若不存在，请说明理由． 图 1 3.2 几何证明及通过几何计算进行说理问题 51.已知二次函数 y＝－x2＋bx＋c 的图像经过点 P(0, 1)与 Q(2, －3)． （1）求此二次函数的解析式； （2）若点 A 是第一象限内该二次函数图像上一点，过点 A 作 x 轴的平行线交二次函数图像 于点 B，分别过点 B、A 作 x 轴的垂线，垂足分别为 C、D，且所得四边形 ABCD 恰为正方形． ①求正方形的 ABCD 的面积； ②联结 PA、PD，PD 交 AB 于点 E，求证：△PAD∽△PEA． 52.某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程： （1）操作发现： 在等腰△ABC 中，AB＝AC，分别以 AB、AC 为斜边，向△ABC 的外侧作等腰直角三角形， 如图 1 所示，其中 DF⊥AB 于点 F，EG⊥AC 于点 G，M 是 BC 的中点，连结 MD 和 ME，则下列 结论正确的是__________（填序号即可）． ①AF＝AG＝ 1 2 AB ；②MD＝ME；③整个图形是轴对称图形；④MD⊥ME． （2）数学思考： 在任意△ABC 中，分别以 AB、AC 为斜边，向△ABC 的外侧作等腰直角三角形，如图 2 所示，M 是 BC 的中点，连结 MD 和 ME，则 MD 与 ME 有怎样的数量关系？请给出证明过程； （3）类比探究： 在任意△ABC 中，仍分别以 AB、AC 为斜边，向△ABC 的内侧作等腰直角三角形，如图 3 所示，M 是 BC 的中点，连结 MD 和 ME，试判断△MDE 的形状．答：_________． 图 1 高中阶段学校招生考试数学试卷 一、选择题（本题有 10 小题，每小题 4 分，共 40 分．每小题只有一个选项是正确的，不选、 多选、错选，均不给分） 1 ． 下 列 各 数 中 ， 最 小 的 数 是 （ ） （A）－1 （B）0 （C）1 （D） 2 2 ． 方 程 4x － 1 ＝ 3 的 解 是 （ ） （A）x＝－1 （B）x＝1 （C）x＝－2 （D）x＝2 3 ． 由 4 个 相 同 的 小 立 方 块 搭 成 的 几 何 体 如 图 所 示 ， 它 的 左 视 图 是 （ ） （A） （B） （C） （D） 4 ． 若 分 式 x－1 x＋2 的 值 为 零 ， 则 x 的 值 是 （ ） （A）0 （B）1 （C）－1 （D）－2 5 ． 抛 物 线 y ＝ (x － 1)2 ＋ 3 的 对 称 轴 是 （ ） （A）直线 x＝1 （B）直线 x＝3 （C）直线 x＝－1 （D）直线 x＝－3 6 ． 已 知 反 比 例 函 数 y ＝ k x 的 图 象 经 过 点 （ 3 ， － 2 ）， 则 k 的 值 是 （ ） （A）－6 （B）6 （C） 2 3 （D）－ 2 3 7．如图，在 Rt△ABC 中，CD 是斜边 AB 上的中线，已知 CD＝ 2，AC＝3，则 sinB 的值是 （ ） C A B D （第 7 题图） 主视方向 （第 3 题图） （A） 2 3 （B） 3 2 （C） 3 4 （D） 4 3 8 ． 已 知 ⊙ O1 和 ⊙ O2 外 切 ， 它 们 的 半 径 分 别 为 2cm 和 5cm ， 则 O1O2 的 长 是 （ ） （A）2cm （B）3cm （C）5cm （D）7cm 9．体育老师对九年级（1）班学生“你最喜欢的体育项目是什么？（只写一项）”的问题进行了 调查，把所得数据绘制成频数分布直方图（如图）．由图可知，最喜欢篮球的频率是 （ ） （A）0.16 （B）0.24 （C）0.3 （D）0.4 10．以 OA 为斜边作等腰直角三角形 OAB，再以 OB 为斜边在△OAB 外侧作等腰直角三角形 OBC， 如此继续，得到 8 个等腰直角三角形（如图），则图中△OAB 与△OHJ 的面积比值是 （ ） （A）32 （B）64 （C）128 （D）256 二、填空题（本题有 6 小题，每小题 5 分，共 30 分） 11．分解因式：x2－9＝___________． 12．布袋中装有 2 个红球，3 个白球，5 个黑球，它们除颜色外均相同，则从袋中任意摸出一个 球是白球．．的概率是__________． 13．如图，菱形 ABCD 中，∠A＝60º，对角线 BD＝8，则菱形 ABCD 的周长等于______． 14．如图，⊙O 的半径为 5，弦 AB＝8，OC⊥AB 于 C，则 OC 的长等于__________． 15．为了奖励兴趣小组的同学，张老师花 92 元钱购买了《智力大挑战》和《数学趣题》两种书．已 知《智力大挑战》每本 18 元．《数学趣题》每本 8 元，则《数学趣题》买了______本． 16．如图，点 A1，A2，A3，A4 在射线 OA 上，点 B1，B2，B3 在射线 OB 上，且 A1B1∥A2B2∥A3B3， A2B1∥A3B2∥A4B3．若△A2B1B2，△A3B2B3 的面积分别为 1，4，则图中三个阴影三角形面积 之和为____________． 三、解答题（本题有 8 小题，共 80 分） 17．（本题 10 分） （1）计算： 8－( 3－1)0＋｜－1｜． B A C D E F G H IO （第 10 题图） 九年级（1）班学生最喜欢体育项目的频数分布直方图 频数（人） 24 20 16 12 8 4 O 4 12 6 20 8 体育项目羽毛球乒乓球 跳绳 篮球 其它 （第 9 题图） A C B D （第 13 题图） （第 14 题图） O C BA （第 16 题图） O A1 A2 A3 A4 A B B1 B2 B3 1 4 （2）我们已经学习了一元二次方程的四种解法：因式分解法，开平方法，配方法和公式法．请 从以下一元二次方程中任选一个．．，并选择你认为适当的方法解这个方程． ①x2－3x＋1＝0；②(x－1)2＝3；③x2－3x＝0；④x2－2x＝4． 18．（本题 8 分）如图，在直角坐标系中，Rt△AOB 的两条直角边 OA，OB 分别在 x 轴的负半轴，y 轴的负半轴上，且 OA＝2，OB＝1．将 Rt△ AOB 绕点 O 按顺时针方向旋转 90º，再把所得的像沿 x 轴正方向平移 1 个单位，得△CDO． （1）写出点 A，C 的坐标； （2）求点 A 和点 C 之间的距离． 19．（本题 9 分）文文和彬彬在证明“有两个角相等的三角形是等腰三 角形”这一命题时，画出图形，写出“已知”，“求证”（如图）， 她们对各自所作的辅助线描述如下： 文文：“过点 A 作 BC 的中垂线 AD，垂足为 D”； 彬彬：“作△ABC 的角平分线 AD”． 数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确 的，而文文的作法需要订正．” （1）请你简要说明文文的辅助线作法错在哪里． （2）根据彬彬的辅助线作法，完成证明过程． 20．（本题 9 分）如图，方格纸中有三个点 A，B，C，要求作一个四边形使这三个点在这个四边 形的边（包括顶点）上，且四边形的顶点在方格的顶点上． （1）在图甲中作出的四边形是中心对称图形但不是轴对称图形； （2）在图乙中作出的四边形是轴对称图形但不是中心对称图形； （3）在图丙中作出的四边形既是轴对称图形又是中心对称图形． （注：图甲、图乙、图丙在答题纸上） 21．（本题 10 分）一次奥运知识竞赛中，一共有 25 道题，答对一题得 10 分，答错（或不答） 一题扣 5 分．设小明同学在这次竞赛中答对 x 道题． （1）根据所给条件，完成下表： y x C B DO A （第 18 题图） （第 19 题图） 已知：如图，在 ABC△ 中， B C   ． 求证： AB AC ． A B D C （第 20 题图） A B C 答题情况 答对 答错或不答 题数 x 每题分值 10 －5 得分 10x （2）若小明同学的竞赛成绩超过 100 分，则他至少答对几道题？ 22．（本题 10 分）一次函数 y＝x－3 的图象与 x 轴，y 轴分别交于点 A，B．一个二次函数 y＝x2 ＋bx＋c 的图象经过点 A，B． （1）求点 A，B 的坐标，并画出一次函数 y＝x－3 的图象； （2）求二次函数的解析式及它的最小值． 23．（本题 10 分）温州皮鞋畅销世界，享誉全球．某皮鞋专卖店老 板对第一季度男女皮鞋的销售收入进行统计，并绘制了扇形统 计图（如图）．由于三月份开展促销活动，男、女皮鞋的销售 收入分别比二月份增长了 40%，60%．已知第一季度男女皮鞋 的销售总收入为 200 万元． （1）一月份销售收入______________万元，二月份销售收入 _____________万元，三月份销售收入__________万元； （2）二月份男、女皮鞋的销售收入各是多少万元？ 24．（本题 14 分）如图，在 Rt△ABC 中，∠A＝90º，AB＝6，AC＝8，D，E 分别是边 AB，AC 的 中点，点 P 从点 D 出发沿 DE 方向运动，过点 P 作 PQ⊥BC 于 Q，过点 Q 作 QR∥BA 交 AC 于 R，当点 Q 与点 C 重合时，点 P 停止运动．设 BQ＝x，QR＝y． （1）求点 D 到 BC 的距离 DH 的长； （2）求 y 关于 x 的函数关系式（不要求写出自变量的取值范围）； （3）是否存在点 P，使△PQR 为等腰三角形？若存在，请求出所有满足要求的 x 的值；若不 存在，请说明理由． A B C D E R P H Q （第 24 题图） （第 23 题图） 一月份 25% 二月份 30% 三月份 45% 第一季度男女皮鞋 销售收入情况统计图 数学参考答案 一、选择题（本题有 10 小题，每小题 4 分，共 40 分） 题号 1 2 3 4 5 6 7 8 9 10 答案 A B C B A A C D D C 二、填空题（本题有 6 小题，每小题 5 分，共 30 分） 题号 11 12 13 14 15 16 答案 ( 3)( 3)x x  0.3 32 3 7 10.5 三、解答题（本题有 8 小题，共 80 分） 17．（本题 10 分） （1）解： 08 ( 3 1) 1 2 2 1 1 2 2        （2）① 1 2 3 5 2x ， ；② 1 2 1 3x  ， ；③ 1 0x  ， 2 3x  ；④ 1 2 1 5x  ， ． 18．（本题 8 分） （1）点 A 的坐标是 ( 2 0) ， ，点C 的坐标是 (1 2)， ． （2）连结 AC ，在 Rt ACD△ 中， 3AD OA OD   ， 2CD  ， 2 2 2 2 22 3 13AC CD AD      ， 13AC  ． 19．（本题 9 分） 解：（1）只要合理即可． （2）证明：作 ABC△ 的角平分线 AD ，则 BAD CAD   ， 又 B C   ， AD AD ， ABD ACD△ ≌△ ， AB AC  ． 20．（本题 9 分）（本题答案不唯一） 21．（本题 10 分） 解：（1） 25 x ； 5(25 )x  （2）根据题意，得10 5(25 ) 100x x   解得 15x  x 的最小正整数解是 16x  答：小明同学至少答对 16 道题． 22．（本题 10 分） 解：（1）令 0y  ，得 3x  ，点 A 的坐标是 (3 0)， 令 0x  ，得 3y   ，点 B 的坐标是 (0 3)， （2）二次函数 2y x bx c   的图象经过点 A B， ， y x C B DO A （第 18 题图） A 图甲（是中心对称图形 但不是轴对称图形） B C 图乙（是轴对称图形但 不是中心对称图形） 图丙（既是轴对称图形 又是中心对称图形） A B C A B C 3 2 1 1 2 O x y 1 1 2 3 4 3y x  A B 0 9 3 3 b c c     ，解得： 2 3 b c      ． 二次函数 2y x bx c   的解析式是 2 2 3y x x   ， 2 22 3 ( 1) 4y x x x      ， 函数 2 2 3y x x   的最小值为 4 ． 23．（本题 10 分） 解：（1）50；60；90． （2）设二月份男、女皮鞋的销售收入分别为 x 万元， y 万元， 根据题意，得 60 (1 40 ) (1 64 ) 90 x y x y        % % ，解得 35 25 x y    ． 答：二月份男、女皮鞋的销售收入分别为 35 万元、25 万元． 24． （本题 14 分） 解：（1） RtA  ， 6AB  ， 8AC  ， 10BC  ． 点 D 为 AB 中点， 1 32BD AB   ． 90DHB A     ， B B   ． BHD BAC△ ∽△ ， DH BD AC BC   ， 3 12810 5 BDDH ACBC      ． （2） QR AB ∥ ， 90QRC A     ． C C   ， RQC ABC△ ∽△ ， RQ QC AB BC   ， 10 6 10 y x  ， 即 y 关于 x 的函数关系式为： 3 65y x   ． （3）存在，分三种情况： ①当 PQ PR 时，过点 P 作 PM QR 于 M ，则QM RM ． 1 2 90     ， 2 90C     ， 1 C   ． 8 4cos 1 cos 10 5C     ， 4 5 QM QP   ， 1 3 6 42 5 12 5 5 x      ， 18 5x  ． ②当 PQ RQ 时， 3 1265 5x   ， 6x  ． ③当 PR QR 时，则 R 为 PQ 中垂线上的点， 于是点 R 为 EC 的中点， 1 1 22 4CR CE AC    ． tan QR BAC CR CA   ， A B C D E R P H Q M 2 1 A B C D E RP H Q A B C D E R P H Q 3 6 65 2 8 x    ， 15 2x  ． 综上所述，当 x 为18 5 或 6 或15 2 时， PQR△ 为等腰三角形． 中考一模数学猜测 一．选择题（共 15 小题） 1．计算：（﹣3）+4 的结果是（ ） A．﹣7 B．﹣1 C．1 D．7 2．为了解在校学生参加课外兴趣小组活动情况，随机调查了 40 名学生，将结果 绘制成了如图所示的频数分布直方图，则参加书法兴趣小组的频率是（ ） A．0.1 B．0.15 C．0.2 D．0.3 3．如图是由 5 个大小相同的正方体摆成的立方体图形，它的左视图是（ ） A． B． C． D． 4．20 位同学在植树节这天共种了 52 棵树苗，其中男生每人种 3 棵，女生每人 种 2 棵．设男生有 x 人，女生有 y 人，根据题意，列方程组正确的是（ ） A． B． C． D． 5．若分式 无意义，则（ ） A．x=2 B．x=﹣1 C．x=1 D．x≠﹣1 6．在一个不透明的盒子中装有 2 个白球，若干个黄球，它们除颜色不同外，其 余均相同，若从中随机摸出一个球，它是白球的概率为 ，则黄球的个数为（ ） A．2 B．3 C．4 D．6 7．若四边形 ABCD 是⊙O 的内接四边形，且∠A：∠B：∠C=1：3：8，则∠D 的 度数是（ ） A．10° B．30° C．80° D．120° 8．下列选项中的图形，不属于中心对称图形的是（ ） A．等边三角形 B．正方形 C．正六边形 D．圆 9．如图，在△ABC 中，∠C=90°，AB=5，BC=3，则 cosA 的值是（ ） A． B． C． D． 10．不等式组 的解是（ ） A．x＜1 B．x≥3 C．1≤x＜3 D．1＜x≤3 11．一次函数 y=2x+4 的图象与 y 轴交点的坐标是（ ） A．（0，﹣4） B．（0，4） C．（2，0） D．（﹣2，0） 12．在半径为 2 的圆中，弦 AB 的长为 2，则 的长等于（ ） A． B． C． D． 13．如图，直线 y=2x+4 与 x，y 轴分别交于点 A，B，以 OB 为底边在 y 轴右侧作 等腰△OBC，将点 C 向左平移 4 个单位，使其对应点 C′恰好落在直线 AB 上，则 点 C 的坐标为（ ） A．（5，2） B．（4，2） C．（3，2） D．（﹣1，2） 14．如图，在方格纸上建立的平面直角坐标系中，Rt△ABC 绕点 C 按顺时针方向 旋转 90°，得到 Rt△FEC，则点 A 的对应点 F 的坐标是（ ） A．（﹣1，1） B．（﹣1，2） C．（1，2） D．（2，1） 15．如图，在△ABC 中，∠B=90°，AB=6cm，BC=8cm．点 P 从点 A 开始沿 AB 边 向点 B 以 1cm/s 的速度移动，点 Q 从点 B 开始沿 BC 边向点 C 以 2cm/s 的速度移 动．若 P、Q 两点同时出发，当点 Q 运动到点 C 时，P、Q 两点同时停止运动， 则在整个运动过程中 PQ 的长度变化情况是（ ） A．先变长后变短 B．一直变短 C．一直变长 D．先变短后变长 二．填空题（共 7 小题） 16．分解因式：x3﹣4x= ． 17．数据 1、5、6、5、6、5、6、6 的众数是 ，方差是 ． 18．如图，直线 AB，CD 被 BC 所截，若 AB∥CD，∠1=45°，∠2=35°，则∠3= 度． 19．如图，⊙O 是正方形 ABCD 的外接圆，点 E 是 上任意一点，则∠BEC 的度 数为 ． 20．如图，将△ABC 绕点 C 按顺时针方向旋转至△A′B′C，使点 A′落在 BC 的延长 线上．已知∠A=27°，∠B=40°，则∠ACB′= 度． 21．如图 1 是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角 形围成．若较短的直角边 BC=5，将四个直角三角形中较长的直角边分别向外延 长一倍，得到图 2 所示的“数学风车”，若△BCD 的周长是 30，则这个风车的外围 周长是 ． 22．如图，若双曲线 y= 与边长为 5 的等边△AOB 的边 OA、AB 分别相交于 C、 D 两点，且 OC=2BD．则实数 k 的值为 ． 三．解答题（共 8 小题） 23．（1）计算： +（﹣3）2﹣（ ﹣1）0． （2）化简：（2+m）（2﹣m）+m（m﹣1）． 24．为了解学生对“垃圾分类”知识的了解程度，某学校对本校学生进行抽样调查， 并绘制统计图，其中统计图中没有标注相应人数的百分比．请根据统计图回答下 列问题： （1）求“非常了解”的人数的百分比． （2）已知该校共有 1200 名学生，请估计对“垃圾分类”知识达到“非常了解”和“比 较了解”程度的学生共有多少人？ 25．在梯形 ABCD 中，AD∥BC，连结 AC，且 AC=BC，在对角线 AC 上取点 E，使 CE=AD，连接 BE． （1）求证：△DAC≌△ECB； （2）若 CA 平分∠BCD，且 AD=3，求 BE 的长． 26．如图，在方格纸中，点 A，B，P 都在格点上．请按要求画出以 AB 为边的格 点四边形，使 P 在四边形内部（不包括边界上），且 P 到四边形的两个顶点的距 离相等． （1）在图甲中画出一个▱ ABCD． （2）在图乙中画出一个四边形 ABCD，使∠D=90°，且∠A≠90°．（注：图甲、乙 在答题纸上） 27．如图，点 C 在以 AB 为直径的⊙O 上，过 C 作⊙O 的切线交 AB 的延长线于 E， AD⊥CE 于 D，连结 AC． （1）求证：AC 平分∠BAD． （2）若 tan∠CAD= ，AD=8，求⊙O 直径 AB 的长． 28．温州享有“中国笔都”之称，其产品畅销全球，某制笔企业欲将 n 件产品运往 A，B，C 三地销售，要求运往 C 地的件数是运往 A 地件数的 2 倍，各地的运费如 图所示．设安排 x 件产品运往 A 地． （1）当 n=200 时，①根据信息填表： A 地 B 地 C 地 合计 产品件数（件） x 2x 200 运费（元） 30x ②若运往 B 地的件数不多于运往 C 地的件数，总运费不超过 4000 元，则有哪几 种运输方案？ （2）若总运费为 5800 元，求 n 的最小值． 29．如图，抛物线 y=x2+bx 经过原点 O，与 x 轴相交于点 A（1，0）， （1）求该抛物线的解析式； （2）在抛物线上方构造一个平行四边形 OABC，使点 B 在 y 轴上，点 C 在抛物线 上，连结 AC． ①求直线 AC 的解析式． ②在抛物线的第一象限部分取点 D，连结 OD，交 AC 于点 E，若△ADE 的面积是 △AOE 面积的 2 倍，这样的点 D 是否存在？若存在，求出点 D 的坐标，若不存 在，请说明理由． 30．如图，A（﹣5，0），B（﹣3，0），点 C 在 y 轴的正半轴上，∠CBO=45°，CD ∥AB．∠CDA=90°．点 P 从点 Q（4，0）出发，沿 x 轴向左以每秒 1 个单位长度 的速度运动，运动时时间 t 秒． （1）求点 C 的坐标； （2）当∠BCP=15°时，求 t 的值； （3）以点 P 为圆心，PC 为半径的⊙P 随点 P 的运动而变化，当⊙P 与四边形 ABCD 的边（或边所在的直线）相切时，求 t 的值． 参考答案与试题解析 一．选择题（共 15 小题） 1．（2016•梅州）计算：（﹣3）+4 的结果是（ ） A．﹣7 B．﹣1 C．1 D．7 【考点】有理数的加法． 【分析】根据异号两数相加，取绝对值较大的数的符号，再用较大的绝对值减去 较小的绝对值，可得答案． 【解答】解：原式=+（4﹣3）=1． 故选：C． 【点评】本题考查了有理数的加法，先确定和的符号，再进行绝对值的运算． 2．（2015•金华模拟）为了解在校学生参加课外兴趣小组活动情况，随机调查了 40 名学生，将结果绘制成了如图所示的频数分布直方图，则参加书法兴趣小组 的频率是（ ） A．0.1 B．0.15 C．0.2 D．0.3 【考点】频数（率）分布直方图． 【分析】根据频率分布直方图可以知道书法兴趣小组的频数，然后除以总人数即 可求出加绘画兴趣小组的频率． 【解答】解：∵根据频率分布直方图知道书法兴趣小组的频数为 8， ∴参加书法兴趣小组的频率是 8÷40=0.2． 故选 C． 【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用 统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和 解决问题． 3．（2016•黄陂区模拟）如图是由 5 个大小相同的正方体摆成的立方体图形，它 的左视图是（ ） A． B． C． D． 【考点】简单组合体的三视图． 【分析】得到从左往右看组合几何体得到的平面图形中包含的 2 列正方形的个数 即可． 【解答】解：从左往右看，得到从左往右 2 列正方形的个数依次为 2，1，故选 C． 【点评】考查三视图中的左视图知识：左视图是从左往右看几何体得到的平面图 形；得到左视图的平面图形中正方形的列数及每列正方形的个数是解决本题的关 键． 4．（2014•温州）20 位同学在植树节这天共种了 52 棵树苗，其中男生每人种 3 棵，女生每人种 2 棵．设男生有 x 人，女生有 y 人，根据题意，列方程组正确的 是（ ） A． B． C． D． 【考点】由实际问题抽象出二元一次方程组． 【分析】设男生有 x 人，女生有 y 人，根据男女生人数为 20，共种了 52 棵树苗， 列出方程组成方程组即可． 【解答】解：设男生有 x 人，女生有 y 人，根据题意得， ． 故选：D． 【点评】此题考查二元一次方程组的实际运用，找出题目蕴含的数量关系是解决 问题的关键． 5．（2011•鹿城区校级模拟）若分式 无意义，则（ ） A．x=2 B．x=﹣1 C．x=1 D．x≠﹣1 【考点】分式有意义的条件． 【分析】根据分式无意义，分母等于 0 列式计算即可得解． 【解答】解：根据题意得，x+1=0， 解得 x=﹣1． 故选 B． 【点评】本题考查了分式有意义的条件，从以下三个方面透彻理解分式的概念： （1）分式无意义 ⇔ 分母为零； （2）分式有意义 ⇔ 分母不为零； （3）分式值为零 ⇔ 分子为零且分母不为零． 6．（2015•中山模拟）在一个不透明的盒子中装有 2 个白球，若干个黄球，它们 除颜色不同外，其余均相同，若从中随机摸出一个球，它是白球的概率为 ，则 黄球的个数为（ ） A．2 B．3 C．4 D．6 【考点】概率公式． 【分析】首先设黄球的个数为 x 个，然后根据题意得： = ，解此分式方程 即可求得答案． 【解答】解：设黄球的个数为 x 个， 根据题意得： = ， 解得：x=4， 经检验，x=4 是原分式方程的解， ∴黄球的个数为 4 个． 故选 C． 【点评】此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总 情况数之比． 7．（2013 秋•鹿城区校级期末）若四边形 ABCD 是⊙O 的内接四边形，且∠A：∠ B：∠C=1：3：8，则∠D 的度数是（ ） A．10° B．30° C．80° D．120° 【考点】圆内接四边形的性质． 【分析】题可设∠A=x，则∠B=3x，∠C=8x；利用圆内接四边形的对角互补，可 求出∠A、∠C 的度数，进而求出∠B 和∠D 的度数，由此得解． 【解答】解：设∠A=x，则∠B=3x，∠C=8x， 因为四边形 ABCD 为圆内接四边形， 所以∠A+∠C=180°， 即：x+8x=180， ∴x=20°， 则∠A=20°，∠B=60°，∠C=160°， 所以∠D=120°， 故选 D． 【点评】本题需仔细分析题意，利用圆内接四边形的性质和四边形的内角和即可 解决问题． 8．（2015•温州）下列选项中的图形，不属于中心对称图形的是（ ） A．等边三角形 B．正方形 C．正六边形 D．圆 【考点】中心对称图形． 【分析】根据中心对称图形的概念求解． 【解答】解：A、不是中心对称图形，故本选项正确； B、是中心对称图形，故本选项错误； C、是中心对称图形，故本选项错误； D、是中心对称图形，故本选项错误． 故选 A． 【点评】本题考查了中心对称图形的概念：中心对称图形是要寻找对称中心，旋 转 180 度后与原图重合． 9．（2015•温州）如图，在△ABC 中，∠C=90°，AB=5，BC=3，则 cosA 的值是 （ ） A． B． C． D． 【考点】锐角三角函数的定义． 【分析】根据锐角的余弦等于邻边比斜边求解即可． 【解答】解：∵AB=5，BC=3， ∴AC=4， ∴cosA= = ． 故选 D． 【点评】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为 对边比斜边，余弦为邻边比斜边，正切为对边比邻边 10．（2015•温州）不等式组 的解是（ ） A．x＜1 B．x≥3C．1≤x＜3 D．1＜x≤3 【考点】解一元一次不等式组． 【分析】先求出每个不等式的解集，再根据找不等式组解集的规律找出不等式组 的解集即可． 【解答】解： ∵解不等式①得：x＞1， 解不等式②得：x≤3， ∴不等式组的解集为 1＜x≤3， 故选 D． 【点评】本题考查了解一元一次不等式组的应用，解此题的关键是能根据不等式 的解集求出不等式组的解集，难度适中． 11．（2014•温州）一次函数 y=2x+4 的图象与 y 轴交点的坐标是（ ） A．（0，﹣4） B．（0，4） C．（2，0） D．（﹣2，0） 【考点】一次函数图象上点的坐标特征． 【分析】在解析式中令 x=0，即可求得与 y 轴的交点的纵坐标． 【解答】解：令 x=0，得 y=2×0+4=4， 则函数与 y 轴的交点坐标是（0，4）． 故选：B． 【点评】本题考查了一次函数图象上点的坐标特征，是一个基础题． 12．（2014•莆田）在半径为 2 的圆中，弦 AB 的长为 2，则 的长等于（ ） A． B． C． D． 【考点】弧长的计算． 【分析】连接 OA、OB，求出圆心角∠AOB 的度数，代入弧长公式求出即可． 【解答】解：连接 OA、OB， ∵OA=OB=AB=2， ∴△AOB 是等边三角形， ∴∠AOB=60°， ∴ 的长为： = ， 故选：C． 【点评】本题考查了弧长公式，等边三角形的性质和判定的应用，注意：已知圆 的半径是 R，弧 AB 对的圆心角的度数是 n°，则弧 AB 的长= ． 13．（2016•温州二模）如图，直线 y=2x+4 与 x，y 轴分别交于点 A，B，以 OB 为 底边在 y 轴右侧作等腰△OBC，将点 C 向左平移 4 个单位，使其对应点 C′恰好落 在直线 AB 上，则点 C 的坐标为（ ） A．（5，2） B．（4，2） C．（3，2） D．（﹣1，2） 【考点】一次函数图象上点的坐标特征；坐标与图形变化﹣平移． 【分析】先求出直线 y=2x+4 与 y 轴交点 B 的坐标为（0，4），再由 C 在线段 OB 的垂直平分线上，得出 C 点纵坐标为 2，将 y=2 代入 y=2x+4，求得 x=﹣1，即可 得到 C′的坐标为（﹣1，2）． 【解答】解：∵直线 y=2x+4 与 y 轴交于 B 点， ∴x=0 时， 得 y=4， ∴B（0，4）． ∵以 OB 为边在 y 轴右侧作等边三角形 OBC， ∴C 在线段 OB 的垂直平分线上， ∴C 点纵坐标为 2． 将 y=2 代入 y=2x+4，得 2=2x+4， 解得 x=﹣1． 则 C′（﹣1，2）， 将其向右平移 4 个单位得到 C（3，2）． 故选：C． 【点评】本题考查了一次函数图象上点的坐标特征，等边三角形的性质，坐标与 图形变化﹣平移，得出 C 点纵坐标为 2 是解题的关键． 14．（2010•沈阳）如图，在方格纸上建立的平面直角坐标系中，Rt△ABC 绕点 C 按顺时针方向旋转 90°，得到 Rt△FEC，则点 A 的对应点 F 的坐标是（ ） A．（﹣1，1） B．（﹣1，2） C．（1，2） D．（2，1） 【考点】坐标与图形变化﹣旋转． 【分析】如图，Rt△ABC 绕点 C 按顺时针方向旋转 90°得到 Rt△FEC，根据旋转的 性质知道 CA=CF，∠ACF=90°，而根据图形容易得到 A 的坐标，也可以得到点 A 的对应点 F 的坐标． 【解答】解：如图， 将 Rt△ABC 绕点 C 按顺时针方向旋转 90°得到 Rt△FEC， ∴根据旋转的性质得 CA=CF，∠ACF=90°， 而 A（﹣2，1）， ∴点 A 的对应点 F 的坐标为（﹣1，2）． 故选 B． 【点评】本题涉及图形体现了新课标的精神，抓住旋转的三要素：旋转中心 C， 旋转方向顺时针，旋转角度 90°，通过画图即可得 F 点的坐标． 15．（2016 春•平阳县月考）如图，在△ABC 中，∠B=90°，AB=6cm，BC=8cm．点 P 从点 A 开始沿 AB 边向点 B 以 1cm/s 的速度移动，点 Q 从点 B 开始沿 BC 边向 点 C 以 2cm/s 的速度移动．若 P、Q 两点同时出发，当点 Q 运动到点 C 时，P、Q 两点同时停止运动，则在整个运动过程中 PQ 的长度变化情况是（ ） A．先变长后变短 B．一直变短 C．一直变长 D．先变短后变长 【考点】动点问题的函数图象． 【分析】根据勾股定理得到 PQ2 与时间 t 的函数关系式，由函数关系式对选项作 出选择． 【解答】解：设 PQ=y，点 P、Q 的运动时间为 t， 则 y2=（6﹣t）2+（2t）2=4t2﹣12t+36=4（t﹣ ）2+27，该函数图象是抛物线，且 顶点坐标是（ ，27）． 则 y2 的值是先变短或变长， 所以 y 即 PQ 的值是先变短或变长， 故选：D． 【点评】考查了动点问题的函数图象．解题关键是深刻理解动点的函数图象，了 解图象中关键点所代表的实际意义，理解动点的完整运动过程． 二．填空题（共 7 小题） 16．（2016•黔西南州）分解因式：x3﹣4x= x（x+2）（x﹣2） ． 【考点】提公因式法与公式法的综合运用． 【分析】应先提取公因式 x，再对余下的多项式利用平方差公式继续分解． 【解答】解：x3﹣4x， =x（x2﹣4）， =x（x+2）（x﹣2）． 故答案为：x（x+2）（x﹣2）． 【点评】本题考查了提公因式法，公式法分解因式，提取公因式后利用平方差公 式进行二次因式分解，分解因式一定要彻底，直到不能再分解为止． 17．（2015•杭州模拟）数据 1、5、6、5、6、5、6、6 的众数是 6 ，方差是 2.5 ． 【考点】方差；众数． 【分析】（1）根据众数的概念，找出数据中出现次数最多的数即为所求； （2）先求平均数，然后根据方差公式计算． 【解答】解：（1）1、5、6、5、6、5、6、6 中，6 出现了四次，次数最多，故 6 为众数； （2）1、5、6、5、6、5、6、6 的平均数为 （1+5+6+5+6+5+6+6）=5， 则 S2= [（1﹣5）2+2×（5﹣5）2+4×（6﹣5）2]=2.5． 故填 6；2.5． 【点评】此题考查了明确众数和方差的意义： （1）众数是一组数据中出现次数最多的那个数据． （2）方差是各变量值与其均值离差平方的平均数，它是测算数值型数据离散程 度的最重要的方法． 18．（2014•温州）如图，直线 AB，CD 被 BC 所截，若 AB∥CD，∠1=45°，∠2=35°， 则∠3= 80 度． 【考点】平行线的性质． 【分析】根据平行线的性质求出∠C，根据三角形外角性质求出即可． 【解答】解：∵AB∥CD，∠1=45°， ∴∠C=∠1=45°， ∵∠2=35°， ∴∠3=∠∠2+∠C=35°+45°=80°， 故答案为：80． 【点评】本题考查了平行线的性质，三角形的外角性质的应用，解此题的关键是 求出∠C 的度数和得出∠3=∠2+∠C． 19．（2015•本溪三模）如图，⊙O 是正方形 ABCD 的外接圆，点 E 是 上任意一 点，则∠BEC 的度数为 45° ． 【考点】圆周角定理；正方形的性质． 【分析】首先连接 OB，OC，由⊙O 是正方形 ABCD 的外接圆，即可求得∠BOC 的度数，又由在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心 角的一半，即可求得∠BEC 的度数． 【解答】解：连接 OB，OC， ∵⊙O 是正方形 ABCD 的外接圆， ∴∠BOC=90°， ∴∠BEC= ∠BOC=45°． 故答案是：45°． 【点评】此题考查了圆周角定理与圆的内接多边形的知识．此题难度不大，注意 准确作出辅助线，注意数形结合思想的应用． 20．（2016•温州）如图，将△ABC 绕点 C 按顺时针方向旋转至△A′B′C，使点 A′ 落在 BC 的延长线上．已知∠A=27°，∠B=40°，则∠ACB′= 46 度． 【考点】旋转的性质． 【分析】先根据三角形外角的性质求出∠ACA′=67°，再由△ABC 绕点 C 按顺时针 方向旋转至△A′B′C，得到△ABC≌△A′B′C，证明∠BCB′=∠ACA′，利用平角即可解 答． 【解答】解：∵∠A=27°，∠B=40°， ∴∠ACA′=∠A+∠B=27°+40°=67°， ∵△ABC 绕点 C 按顺时针方向旋转至△A′B′C， ∴△ABC≌△A′B′C， ∴∠ACB=∠A′CB′， ∴∠ACB﹣∠B′CA=∠A′CB﹣∠B′CA， 即∠BCB′=∠ACA′， ∴∠BCB′=67°， ∴∠ACB′=180°∠ACA′﹣∠BCB′=180°﹣67°﹣67°=46°， 故答案为：46． 【点评】本题考查了旋转的性质，解决本题的关键是由旋转得到△ABC≌△A′B′C． 21．（2014 秋•永嘉县校级期中）如图 1 是我国古代著名的“赵爽弦图”的示意图， 它是由四个全等的直角三角形围成．若较短的直角边 BC=5，将四个直角三角形 中较长的直角边分别向外延长一倍，得到图 2 所示的“数学风车”，若△BCD 的周 长是 30，则这个风车的外围周长是 76 ． 【考点】勾股定理的证明． 【分析】由题意∠ACB 为直角，利用勾股定理求得外围中一条边，又由 AC 延伸 一倍，从而求得风车的一个轮子，进一步求得四个． 【解答】解：依题意，设“数学风车”中的四个直角三角形的斜边长为 x，AC=y， 则 x2=4y2+52， ∵△BCD 的周长是 30， ∴x+2y+5=30 则 x=13，y=6． ∴这个风车的外围周长是：4（x+y）=4×19=76． 故答案是：76． 【点评】本题考查了勾股定理在实际情况中的应用，注意隐含的已知条件来解答 此类题． 22．（2014•武汉）如图，若双曲线 y= 与边长为 5 的等边△AOB 的边 OA、AB 分 别相交于 C、D 两点，且 OC=2BD．则实数 k 的值为 4 ． 【考点】反比例函数与一次函数的交点问题；等边三角形的性质． 【分析】过点 C 作 CE⊥x 轴于点 E，过点 D 作 DF⊥x 轴于点 F，设 OC=2x，则 BD=x， 分别表示出点 C、点 D 的坐标，代入函数解析式求出 k，继而可建立方程，解出 x 的值后即可得出 k 的值． 【解答】解：过点 C 作 CE⊥x 轴于点 E，过点 D 作 DF⊥x 轴于点 F， 设 OC=2x，则 BD=x， 在 Rt△OCE 中，∠COE=60°， 则 OE=x，CE= x， 则点 C 坐标为（x， x）， 在 Rt△BDF 中，BD=x，∠DBF=60°， 则 BF= x，DF= x， 则点 D 的坐标为（5﹣ x， x）， 将点 C 的坐标代入反比例函数解析式可得：k= x2， 将点 D 的坐标代入反比例函数解析式可得：k= x﹣ x2， 则 x2= x﹣ x2， 解得：x1=2，x2=0（舍去）， 故 k= x2= ×4=4 ． 故答案为：4 ． 【点评】本题考查了反比例函数图象上点的坐标特征，解答本题关键是利用 k 的 值相同建立方程，有一定难度． 三．解答题（共 8 小题） 23．（2016•温州）（1）计算： +（﹣3）2﹣（ ﹣1）0． （2）化简：（2+m）（2﹣m）+m（m﹣1）． 【考点】实数的运算；单项式乘多项式；平方差公式；零指数幂． 【分析】（1）直接利用二次根式的性质结合零指数幂的性质分别分析得出答案； （2）直接利用平方差公式计算，进而去括号得出答案． 【解答】解：（1）原式=2 +9﹣1 =2 +8； （2）（2+m）（2﹣m）+m（m﹣1） =4﹣m2+m2﹣m =4﹣m． 【点评】此题主要考查了实数运算以及整式的混合运算，正确化简各数是解题关 键． 24．（2016•温州）为了解学生对“垃圾分类”知识的了解程度，某学校对本校学生 进行抽样调查，并绘制统计图，其中统计图中没有标注相应人数的百分比．请根 据统计图回答下列问题： （1）求“非常了解”的人数的百分比． （2）已知该校共有 1200 名学生，请估计对“垃圾分类”知识达到“非常了解”和“比 较了解”程度的学生共有多少人？ 【考点】扇形统计图；用样本估计总体． 【分析】（1）根据扇形统计图可以求得“非常了解”的人数的百分比； （2）根据扇形统计图可以求得对“垃圾分类”知识达到“非常了解”和“比较了解” 程度的学生共有多少人． 【解答】解：（1）由题意可得， “非常了解”的人数的百分比为： ， 即“非常了解”的人数的百分比为 20%； （2）由题意可得， 对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有：1200× =600（人）， 即对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有 600 人． 【点评】本题考查扇形统计图好、用样本估计总体，解题的关键是明确扇形统计 图的特点，找出所求问题需要的条件． 25．（2015•桐庐县模拟）在梯形 ABCD 中，AD∥BC，连结 AC，且 AC=BC，在对 角线 AC 上取点 E，使 CE=AD，连接 BE． （1）求证：△DAC≌△ECB； （2）若 CA 平分∠BCD，且 AD=3，求 BE 的长． 【考点】全等三角形的判定与性质． 【分析】（1）由平行可得到∠DAC=∠ECB，结合条件可证明△DAC≌△ECB； （2）由条件可证明 DA=DC，结合（1）的结论可得到 BE=CD，可求得 BE 的长． 【解答】（1）证明：∵AD∥BC， ∴∠DAC=∠ECB， 在△DAC 和△ECB 中， ， ∴△DAC≌△ECB（SAS）； （2）解：∵CA 平分∠BCD， ∴∠ECB=∠DCA，且由（1）可知∠DAC=∠ECB， ∴∠DAC=∠DCA， ∴CD=DA=3， 又∵由（1）可得△DAC≌△ECB， ∴BE=CD=3． 【点评】本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法 （SSS、SAS、ASA、AAS 和 HL）和性质（对应边、对应角相等）是解题的关键． 26．（2016•温州）如图，在方格纸中，点 A，B，P 都在格点上．请按要求画出 以 AB 为边的格点四边形，使 P 在四边形内部（不包括边界上），且 P 到四边形 的两个顶点的距离相等． （1）在图甲中画出一个▱ ABCD． （2）在图乙中画出一个四边形 ABCD，使∠D=90°，且∠A≠90°．（注：图甲、乙 在答题纸上） 【考点】平行四边形的性质． 【分析】（1）先以点 P 为圆心、PB 长为半径作圆，会得到 4 个格点，再选取合 适格点，根据平行四边形的判定作出平行四边形即可； （2）先以点 P 为圆心、PB 长为半径作圆，会得到 8 个格点，再选取合适格点记 作点 C，再以 AC 为直径作圆，该圆与方格网的交点任取一个即为点 D，即可得． 【解答】解：（1）如图①： ． （2）如图②， ． 【点评】本题主要考查了中垂线性质，平行四边形的判定、性质及圆周角定理的 应用，熟练掌握这些判定、性质及定理并灵活运用是解题的关键． 27．（2016•温州模拟）如图，点 C 在以 AB 为直径的⊙O 上，过 C 作⊙O 的切线 交 AB 的延长线于 E， AD⊥CE 于 D，连结 AC． （1）求证：AC 平分∠BAD． （2）若 tan∠CAD= ，AD=8，求⊙O 直径 AB 的长． 【考点】切线的性质；解直角三角形． 【分析】（1）连接 OC，由 DE 为圆 O 的切线，得到 OC 垂直于 CD，再由 AD 垂直 于 DE，得到 AD 与 OC 平行，得到一对内错角相等，根据 OA=OC，利用等边对等 角得到一对角相等，等量代换即可得证； （2）在直角三角形 ADC 中，利用锐角三角函数定义求出 CD 的长，根据勾股定 理求出 AD 的长，由三角形 ACD 与三角形 ABC 相似，得到对应边成比例，即可求 出 AB 的长． 【解答】证明：（1）连结 OC， ∵DE 是⊙O 的切线， ∴OC⊥DE， ∵AD⊥CE， ∴AD∥OC， ∵OA=OC， ∴∠DAC=∠ACO=∠CAO， ∴AC 平分∠BAD； （2）解：∵AD⊥CE，tan∠CAD= ，AD=8， ∴CD=6， ∴AC=10， ∵AB 是⊙O 的直径， ∴∠ACB=90°=∠D， ∵∠DAC=∠CAO， ∴△ACD∽△ABC， ∴AB：AC=AC：AD， ∴AB= ． 【点评】此题考查了切线的性质，以及解直角三角形，熟练掌握切线的判定与性 质是解本题的关键． 28．（2012•温州）温州享有“中国笔都”之称，其产品畅销全球，某制笔企业欲将 n 件产品运往 A，B，C 三地销售，要求运往 C 地的件数是运往 A 地件数的 2 倍， 各地的运费如图所示．设安排 x 件产品运往 A 地． （1）当 n=200 时，①根据信息填表： A 地 B 地 C 地 合计 产品件数（件） x 2x 200 运费（元） 30x ②若运往 B 地的件数不多于运往 C 地的件数，总运费不超过 4000 元，则有哪几 种运输方案？ （2）若总运费为 5800 元，求 n 的最小值． 【考点】一次函数的应用；一元一次不等式组的应用． 【分析】（1）①运往 B 地的产品件数=总件数 n﹣运往 A 地的产品件数﹣运往 B 地的产品件数；运费=相应件数×一件产品的运费； ②根据运往 B 地的件数不多于运往 C 地的件数，总运费不超过 4000 元列出不等 式组，求得正整数解的个数即可； （2）总运费=A 产品的运费+B 产品的运费+C 产品的运费，进而根据函数的增减 性及（1）中②得到的 x 的取值求得 n 的最小值即可． 【解答】解：（1）①根据信息填表 A 地 B 地 C 地 合计 产品件数（件） 200﹣3x 运费 1600﹣24x 50x 56x+1600 ②由题意，得 ， 解得 40≤x≤42 ， ∵x 为正整数， ∴x=40 或 41 或 42， ∴有三种方案，分别是（i）A 地 40 件，B 地 80 件，C 地 80 件； （ii）A 地 41 件，B 地 77 件，C 地 82 件； （iii）A 地 42 件，B 地 74 件，C 地 84 件； （2）由题意，得 30x+8（n﹣3x）+50x=5800， 整理，得 n=725﹣7x． ∵n﹣3x≥0， ∴725﹣7x﹣3x≥0， ∴﹣10x≥﹣725， ∴x≤72.5， 又∵x≥0， ∴0≤x≤72.5 且 x 为正整数． ∵n 随 x 的增大而减少， ∴当 x=72 时，n 有最小值为 221． 【点评】考查一次函数的应用；得到总运费的关系式是解决本题的关键；注意结 合自变量的取值得到 n 的最小值． 29．（2016•瓯海区一模）如图，抛物线 y=x2+bx 经过原点 O，与 x 轴相交于点 A （1，0）， （1）求该抛物线的解析式； （2）在抛物线上方构造一个平行四边形 OABC，使点 B 在 y 轴上，点 C 在抛物线 上，连结 AC． ①求直线 AC 的解析式． ②在抛物线的第一象限部分取点 D，连结 OD，交 AC 于点 E，若△ADE 的面积是 △AOE 面积的 2 倍，这样的点 D 是否存在？若存在，求出点 D 的坐标，若不存 在，请说明理由． 【考点】二次函数综合题． 【分析】（1）把 A 点坐标代入 y=x2+bx 中求出 b 的值即可得到抛物线解析式； （2）①根据平行四边形的性质得 BC=OA=1，BC∥OA，则 C 点的横坐标为﹣1， 再计算对应的函数值即可得到 C 点坐标，然后利用待定系数法求直线 AC 的解析 式； ②分别作 DM⊥x 轴于 M，EN⊥x 轴于 N，如图，根据三角形面积公式可判断 DE=2OE，再证明△ONE∽△OMD，则利用相似比可得 = = ，于是设 E（t， ﹣t+1），则 D（3t，﹣3t+3），然后把 D（3t，﹣3t+3）代入 y=x2﹣x 得关于 t 的一 元二次方程，再解方程即可得到满足条件的 D 点坐标． 【解答】解：（1）把 A（1，0）代入 y=x2+bx 得 1+b=0，解得 b=﹣1， 所以抛物线解析式为 y=x2﹣x； （2）①∵四边形 OABC 为平行四边形， ∴BC=OA=1，BC∥OA， ∴C 点的横坐标为﹣1， 当 x=﹣1 时，y=x2﹣x=1﹣（﹣1）=2，则 C（﹣1，2）， 设直线 AC 的解析式为 y=mx+n， 把 A（1，0），C（2，﹣1）代入得 ，解得 ， 所以直线 AC 的解析式为 y=﹣x+1； ②存在． 分别作 DM⊥x 轴于 M，EN⊥x 轴于 N，如图， ∵△ADE 的面积是△AOE 面积的 2 倍， ∴DE=2OE， ∵EN∥DM， ∴△ONE∽△OMD， ∴ = = = ， 设 E（t，﹣t+1），则 D（3t，﹣3t+3） 把 D（3t，﹣3t+3）代入 y=x2﹣x 得 9t2﹣3t=﹣3t+3，解得 t1= ，t2=﹣ （舍 去）， ∴点 D 的坐标为（ ，﹣ +3）． 【点评】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征 和平行四边形的性质；会利用待定系数法求函数的解析式；理解坐标与图形的性 质；灵活利用相似比求线段之间的关系． 30．（2012•河北）如图，A（﹣5，0），B（﹣3，0），点 C 在 y 轴的正半轴上， ∠CBO=45°，CD∥AB．∠CDA=90°．点 P 从点 Q（4，0）出发，沿 x 轴向左以每 秒 1 个单位长度的速度运动，运动时时间 t 秒． （1）求点 C 的坐标； （2）当∠BCP=15°时，求 t 的值； （3）以点 P 为圆心，PC 为半径的⊙P 随点 P 的运动而变化，当⊙P 与四边形 ABCD 的边（或边所在的直线）相切时，求 t 的值． 【考点】切线的性质；坐标与图形性质；勾股定理；解直角三角形． 【分析】（1）由∠CBO=45°，∠BOC 为直角，得到△BOC 为等腰直角三角形，又 OB=3，利用等腰直角三角形 AOB 的性质知 OC=OB=3，然后由点 C 在 y 轴的正半 轴可以确定点 C 的坐标； （2）需要对点 P 的位置进行分类讨论：①当点 P 在点 B 右侧时，如图 2 所示， 由∠BCO=45°，用∠BCO﹣∠BCP 求出∠PCO 为 30°，又 OC=3，在 Rt△POC 中， 利用锐角三角函数定义及特殊角的三角函数值求出 OP 的长，由 PQ=OQ+OP 求出 运动的总路程，由速度为 1 个单位/秒，即可求出此时的时间 t；②当点 P 在点 B 左侧时，如图 3 所示，用∠BCO+∠BCP 求出∠PCO 为 60°，又 OC=3，在 Rt△POC 中，利用锐角三角函数定义及特殊角的三角函数值求出 OP 的长，由 PQ=OQ+OP 求出运动的总路程，由速度为 1 个单位/秒，即可求出此时的时间 t； （3）当⊙P 与四边形 ABCD 的边（或边所在的直线）相切时，分三种情况考虑： ①当⊙P 与 BC 边相切时，利用切线的性质得到 BC 垂直于 CP，可得出∠BCP=90°， 由∠BCO=45°，得到∠OCP=45°，即此时△COP 为等腰直角三角形，可得出 OP=OC， 由 OC=3，得到 OP=3，用 OQ﹣OP 求出 P 运动的路程，即可得出此时的时间 t； ②当⊙P 与 CD 相切于点 C 时，P 与 O 重合，可得出 P 运动的路程为 OQ 的长， 求出此时的时间 t； ③当⊙P 与 AD 相切时，利用切线的性质得到∠DAO=90°，得到此时 A 为切点， 由 PC=PA，且 PA=9﹣t，PO=t﹣4，在 Rt△OCP 中，利用勾股定理列出关于 t 的方 程，求出方程的解得到此时的时间 t． 综上，得到所有满足题意的时间 t 的值． 【解答】解：（1）∵∠BCO=∠CBO=45°， ∴OC=OB=3， 又∵点 C 在 y 轴的正半轴上， ∴点 C 的坐标为（0，3）； （2）分两种情况考虑： ①当点 P 在点 B 右侧时，如图 2， 若∠BCP=15°，得∠PCO=30°， 故 PO=CO•tan30°= ，此时 t=4+ ； ②当点 P 在点 B 左侧时，如图 3， 由∠BCP=15°，得∠PCO=60°， 故 OP=COtan60°=3 ， 此时，t=4+3 ， ∴t 的值为 4+ 或 4+3 ； （3）由题意知，若⊙P 与四边形 ABCD 的边相切时，有以下三种情况： ①当⊙P 与 BC 相切于点 C 时，有∠BCP=90°， 从而∠OCP=45°，得到 OP=3，此时 t=1； ②当⊙P 与 CD 相切于点 C 时，有 PC⊥CD，即点 P 与点 O 重合，此时 t=4； ③当⊙P 与 AD 相切时，由题意，得∠DAO=90°， ∴点 A 为切点，如图 4，PC2=PA2=（9﹣t）2，PO2=（t﹣4）2， 于是（9﹣t）2=（t﹣4）2+32，即 81﹣18t+t2=t2﹣8t+16+9， 解得：t=5.6， ∴t 的值为 1 或 4 或 5.6． 【点评】此题考查了切线的性质，坐标与图形性质，勾股定理，等腰直角三角形 的判定与性质，锐角三角函数定义，利用了数形结合及分类讨论的思想，熟练掌 握切线的性质是解本题的关键． 九年级第三次模拟考试 数学试题卷 一、选择题（本大题共 10 小题，每题 3 分，共计 30 分．在每小题 所给出的四个选项中， 只有一项是符合题目要求的，请用 2B 铅笔把答题．．卷．上相应的答案．．．．．．涂黑．） 1．－2 的倒数是…………………………………………………………………………………… （ ▲ ） A．2 B．－2 C．1 2 D．－1 2 2．下列计算正确的是……………………………………………………………………………… （ ▲ ） A．3a 2－ a2＝ 3 B．a2· a 4＝ a8 C．(a3) 2＝ a 6 D．a 6÷ a2＝ a3 3．一组数据：2，－ 1，0，3，－ 3，2 ．则这组数据的中位数和众数分别是……………… （ ▲ ） A．0，2 B．1.5，2 C．1，2 D．1，3 4．不等式组 x≤1， x＞－1 的解集是……………………………………………………………………… （ ▲ ） A．x＞－1 B．x≤1 C．x＜－1 D．－1＜x≤1 5．将抛物线 y＝x2 平移得到抛物线 y＝(x＋3)2，则这个平移过程正确的是……………… （ ▲ ） A．向左平移 3 个单位 B．向右平移 3 个单位 C．向上平移 3 个单位 D．向下平移 3 个单位 6．在一个直角三角形中，有一个锐角等于 40°，则另一个锐角的度数是…………………… （ ▲ ） A．40° B．50° C．60° D．70° 7．一个多边形的内角和等于它的外角和，则这个多边形的边数为…………………………… （ ▲ ） A．3 B．4 C．5 D．6 8．如图，AB 是⊙O 直径，若∠AOC ＝140°，则∠D 的度数是………………………………（ ▲ ） A．20° B．30° C．40° D．70° 9．如图，E 是□ABCD 的 AD 边上一点，CE 与 BA 的延长线交于点 F，则下列比例式：①FB CD ＝ FC CE ；②AE ED ＝AF AB ；③FA FB ＝AE AD ；④ AE EC ＝ FE ED ，其中一定成立的是………………………………… （ ▲ ） A．①②③④ B．①②③ C．①②④ D．①② 10．如图，P 为正方形 ABCD 对角线 BD 上一动点，若 AB＝2，则 AP＋BP＋CP 的最小值为… （ ▲ ） A． 2＋ 5cm B． 2＋ 6 C．4 D．3 2 二、填空题（本大题共 8 小题，每题 2 分，共计 16 分．请把答案直接填写在答题．．卷．相应位．．． 置．上．） 11．要使分式 1 x＋2 有意义，则 x 的取值范围是 ▲ ． 12．分解因式：a2－4＝ ▲ ． 13．2015 年 12 月，无锡市梁溪区正式成立．梁溪区包含原崇安区、南长区、北塘区，总人 口近 1015000 人，这个人口数据用科学记数法可表示为 ▲ ． 14．点(1，y1)、(2，y2)都在一次函数 y＝kx＋b(k＞0)的图象上，则 y1 ▲ y2（填“＞”或“＝” 或“＜”）． 15．用一张边长为 4πcm 的正方形纸片刚好围成一个圆柱的侧面，则该圆柱的底面圆的半 径长 为 ▲ cm． 16．如图，在正方形网格中，△ABC 的顶点都在格点上，则 tan∠ACB 的值为 ▲ ． 17．在锐角△ABC 中，已知其两边 a＝1，b＝3，则第三边 c 的取值范围为 ▲ ． 18．如图，在 Rt△OAB 中，∠AOB＝90°，OA＝8，AB＝10，⊙O 的半径为 4．点 P 是 AB 上的一动点，过点 P 作⊙O 的一条切线 PQ，Q 为切点．设 AP＝x (0≤x≤10)，PQ2＝y， 则 y 与 x 的函数关系式为 ▲ ． D B O A C （第 8 题） （第 9 题） F D E CB A A B C D P （第 10 题） A B C （第 16 题） （第 18 题） A PQ B O A B C D 三、解答题（本大题共 10 小题，共计 84 分．解答需写出必要的文字说明或演算步骤.） 19．（本题满分 8 分）计算： （1） 4－(－3)2＋(－0.2)0； （2）(x＋3)(x―3)―(x―2)2． 20．（本题满分 8 分） （1）解方程：x2－4x＋1＝0； （2）解方程组： x－3y＝1，…………① 2(x－3)＝y＋6．……② 21．（本题满分 8 分）如图，BD 为□ABCD 的对角线，AE⊥BD，CF⊥BD，垂足分别为 E、F． 求证：BE＝DF． 22．（本题满分 8 分）有三个质地、大小都相同的小球分别标上数字 2，－2，3 后放入一个 不透明的口袋搅匀，任意摸出一个小球，记下数字 a 后，放回口袋中搅匀，再任意摸出 一个小球，又记下数字 b．这样就得到一个点的坐标(a，b)． （1）求这个点(a，b)恰好在函数 y＝－x 的图像上的概率．（请用“画树状图”或“列表” 等方法给出分析过程，并求出结果） （2）如果再往口袋中增加 n(n≥1)个标上数字 2 的小球，按照同样的操作过程，所得到 的点(a，b)恰好在函数 y＝－x 的图像上的概率是 ▲ （请用含 n 的代数式直接写 出结果）． 23．（本题满分 8 分）如图，在矩形 ABCD 中，AB＝4，BC＝6，若点 P 在 AD 边上，连接 BP、 PC，使得△BPC 是一个等腰三角形． （1）用尺规作图画出符合要求的点 P．（保留作图痕迹，不要求写做法） （2）求出 PA 的长． A B C D E F 24．（本题满分 8 分）无锡有丰富的旅游产品．某校九年级（1）班的同学就部分旅游产品的 喜爱情况对部分游客随机调查，要求游客在列举的旅游产品中选出最喜爱的产品，且 只能选一项，以下是同学们整理的不完整的统计图： 根据以上信息完成下列问题： （1）请将条形统计图补充完整． （2）参与随机调查的游客有 ▲ 人；在扇形统计图中，A 部分所占的圆心角是 ▲ 度． （3）根据调查结果估计在 2000 名游客中最喜爱惠山泥人的约有 ▲ 人． 25．（本题满分 10 分）初夏五月，小明和同学们相约去森林公园游玩．从公园入口处到景点 只有一条长 15km 的观光道路．小明先从入口处出发匀速步行前往景点，1.5 h 后，迟 到的另 3 位同学在入口处搭乘小型观光车（限载客 3 人）匀速驶往景点，结果反而比 小明早到 45 min．已知小型观光车的速度是步行速度的 4 倍． （1）分别求出小型观光车和步行的速度． （2）如果小型观光车在某处让这 3 位同学下车步行前往景点(步行速度和小明相同)， 观光车立即返回接载正在步行的小明后直接驶往景点，并正好和这 3 位同学同时到 达．求这样做可以使小明提前多长时间到达景点？（上下车及车辆调头时间忽略不计） 26．（本题满分 8 分）如图，正方形 ABCD 的对角线相交于点 O，∠CAB 的平分线分别交 BD、BC 于 E、F，作 BH⊥AF 于点 H，分别交 AC、CD 于点 G、P，连结 GE、GF． （1）试判断四边形 BEGF 的形状并说明理由． A：酱排骨 B：惠山泥人 C：宜兴紫砂陶 D：油面筋 E：茶叶 （2）求AE PG 的值． 27．（本题满分 8 分）已知，如图 1，直线 l 与反比例函数 y＝k x(k＞0)位于第一象限的图像相 交于 A、B 两点，并与 y 轴、x 轴分别交于 E、F． （1）试判断 AE 与 BF 的数量关系并说明理由． （2）如图 2，若将直线 l 绕点 A 顺时针旋转，使其与反比例函数 y＝k x 的另一支图像相交， 设交点为 B．试判断 AE 与 BF 的数量关系是否依然成立？请说明理由． A B CD P E FO G H （图 1） x y O A E F B l （图 2） x y O B A E F l （图 1） （图 2） （图 3） 28．（本题满分 10 分）如图 1，二次函数 y＝ax2－2ax－3a（a＜0）的图象与 x 轴交于 A、B 两点（点 A 在点 B 的右侧），与 y 轴的正半轴交于点 C，顶点为 D． （1）求顶点 D 的坐标（用含 a 的代数式表示）． （2）若以 AD 为直径的圆经过点 C． ①求 a 的值． ②如图 2，点 E 是 y 轴负半轴上一点，连接 BE，将△OBE 绕平面内某一点旋转 180°， 得到△PMN（点 P、M、N 分别和点 O、B、E 对应），并且点 M、N 都在抛物线上， 作 MF⊥x 轴于点 F，若线段 BF＝2MF，求点 M、N 的坐标． ③如图 3，点 Q 在抛物线的对称轴上，以 Q 为圆心的圆过 A、B 两点，并且和直线 CD 相切，求点 Q 的坐标． 答案及评分说明 一、选择题（每小题 3 分，共 30 分） 1．D 2．C 3．C 4．D 5．A 6．B 7．B 8．A 9．B 10．B 二、填空题（每小题 2 分，共 16 分） 11．x≠－2 12．(a＋2)(a－2) 13．1.015×106 14．＜ 15．2 16．3 5 17．2 2＜c＜ 10 18．y＝x2－64 5 x＋48 三、解答题（本大题共 10 小题，共 84 分．注：解答方法及步骤不唯一，请参考评分！） 19．解：（1）原式＝2－9＋1＝－6．……………………………………………………………… （4 分） （2）原式＝x2－9－x2＋4x－4＝4x－13．……………………………………………… （4 分） 20．解：（1）x＝4± 16－4 2 ，………………（2 分） ∴x＝2± 3．……………………… （4 分） （2）由①，得 x＝1＋3y③，…………………………………………………………… （1 分） 由②，得 2x－y＝12④，…………………………………………………………… （2 分） 把③代入④得 2＋6y－y＝12．解得 y＝2．……………………………………… （3 分） 把 y＝2 代入③得 x＝7．∴ x＝7， y＝2．………………………………………………… （4 分） 21．证：∵□ABCD，∴AB∥CD，AB＝CD. ……………………………………………………（4 分） ∴∠ABD＝∠CDB．……………………………………………………………………（5 分） ∵AE⊥BD，CF⊥BD，∴∠AEB＝∠CFD．…………………………………………（6 分） 在△ABE 和△CDF 中， ∠ABE＝∠CDF， ∠AEB＝∠CFD， AB＝CD， ∴△ABE≌△CDF．…………………（7 分） ∴BE＝DF．……………………………………………………………………………… （8 分） 22．解：（1）画树状图： 或：列表： 2 －2 3 2 (2，2) (2, －2) (2，3) －2 (－2，2) (－2，－2) (－2，3) 3 (3，2) (3，－2) (3，3) …………（3 分） a b 2 2 (2，2) －2 (2，－2) 3 (2，3) ……（3分） －2 2 (－2，2) －2 (－2，－2) 3 (－2，3) 3 2 (3，2) －2 (3，－2) (a，b) 共有 9 种等可能的结果，其中符合要求的结果有 2 种，…………………………………（4 分） ∴P（点在函数图像上）＝2 9 ． ……………………………………………………………… （6 分） （2）2(n＋1) (n＋3)2.…………………………………………………………………………………（8 分） 23．解：（1）图略． ……………………………………………………………………………… （3 分） （2）当 BC＝BP 时，PA＝2 5，………………………………………………………… （5 分） 当 CB＝CP 时，PA＝AD－PD＝6－2 5，………………………………………（6 分） 当 PB＝PC 时，PA＝1 2 AD＝3．……………………………………………………（7 分） 综上，PA 的长为 2 5，6－2 5，3．………………………………………………… （8 分） 24．解：（1）图略．………（2 分） （2）400，72．………（6 分） （3）560．………… （8 分） 25．解：（1）设步行的速度为 x km/h，则小型观光车的速度为 4x km/h．…………………… （1 分） 由题意得15 x ＝1.5＋15 4x ＋45 60 ，………………（3 分）解得 x＝5．………………………… （4 分） 经检验，x＝5 是原方程的根，……………………………………………………………… （5 分） 答：步行的速度为 5 km/h，小型观光车的速度为 20 km/h．…………………………… （6 分） （2）设观光车在距景点 m km 处把人放下， 此时观光车行驶用时15－m 20 h，小明已步行路程为 5×(1.5＋15－m 20 )＝45－m 4 km. ∴观光车返回与小明相遇用时 15－m－45－m 4 20＋5 ＝15－3m 100 h． 由题意得15－3m 100 ×2＋m 20 ＝m 5 ，…………（8 分）解得 m＝30 21 ．………………………（9 分） 3 (3，3) 小明此时全程用时为 1.5＋15－m 20 ＋m 5 ＝69 28 h，∴小明可提前15 5 －69 28 ＝15 28 h．………… （10 分） 26．解（1）四边形 BEGF 是菱形，理由如下：…………………………………………………（1 分） ∵∠GAH＝∠BAH，AH＝AH ， ∠AHG＝∠AHB＝90°， ∴△AHG≌△AHB．∴GH＝BH． ∴AF 是线段 BG 的垂直平分线，∴EG＝EB，FG＝FB．…………………………………（2 分） ∵∠BEF＝∠BAF＋∠ABE＝67.5°，∠BFE＝90°－∠BAF＝67.5° ∴∠BEF＝∠BFE．∴EB＝FB．…………… ………………………………………………（3 分） ∴EG＝EB＝FB＝FG．∴四边形 BEGF 是菱形．…………………………………………（4 分） （2）设 OA＝OB＝OC＝a，菱形 BEGF 的边长为 b． ∵四边形 BEGF 是菱形，∴GF∥OB， ∴∠CGF＝∠COB＝90°， ∴∠GFC＝∠GCF＝45°， ∴CG＝GF＝b．………………………………………………（5 分） ∵四边形 ABCD 是正方形，∴OA＝OB，∠AOE＝∠BOG＝90° ∵BH⊥AF，∴∠GAH＋∠AGH＝90°＝∠OBG＋∠AGH． ∴∠GAH＝∠OBG，∴△OAE≌△OBG．∴OG＝OE＝a－b．…………………………（6 分） ∵在 Rt△GOE 中，GE＝ 2OG，∴b＝ 2(a－b)，整理得 a＝2＋ 2 2 b．………………（7 分） ∴AC＝2a＝(2＋ 2)b，AG＝AC－CG＝(1＋ 2)b． ∵PC∥AB， ∴BG PG ＝AG CG ＝(1＋ 2)b b ＝1＋ 2， 由△OAE≌△OBG 得 AE＝BG，∴AE PG ＝1＋ 2．…………………………………………（8 分） 27．解（1）AE＝BF，理由如下：………………………………………………………………（1 分） 作 AM⊥y 轴，BN⊥x 轴，连 MN、OA、OB、BM、AN． ∵AM∥x 轴，∴S△AMN＝S△AM O＝k 2 ．同理，S△BMN＝S△BNO＝k 2 ．∴S△AMN＝S△BMN．………（2 分） 即 A、B 两点到 MN 的距离相等，且 A、B 位于 MN 同侧，故 AB∥MN．…………… （3 分） ∴四边形 AMNF 与 BNME 均为平行四边形，∴AM＝FN，EM＝BN． 又∵∠AME＝∠BNF＝90°，∴△EMA≌△BNF，∴AE＝BF．…………………………（4 分） （2）结论依然成立，AE＝BF．……………………………………………………………… （5 分） 理由略，与（1）类似．………………………………………………………………（8 分） 28．解：(1)∵y＝ax2－2ax－3a＝a(x－1)2－4a，∴D(1，－4a)．……………………………… （2 分） (2)①∵以 AD 为直径的圆经过点 C，∴△ACD 为直角三角形，且∠ACD＝90°；……… （3 分） 由 y＝ax2－2ax－3a＝a(x－3)(x＋1)知，A(3，0)、B(－1，0)、C(0，－3a)，则： AC2＝9a2＋9、CD2＝a2＋1、AD2＝16a2＋4 由勾股定理得：AC2＋CD2＝AD2，即：9a2＋9＋a2＋1＝16a2＋4， 化简，得：a2＝1，由 a＜0，得：a＝－1……………………………………………… （4 分） ②∵a＝－1，∴抛物线的解析式：y＝－x2＋2x＋3，D(1，4)． ∵将△OBE 绕平面内某一点旋转 180°得到△PMN， ∴PM∥x 轴，且 PM＝OB＝1； 设 M(x，－x2＋2x＋3)，则 OF＝x，MF＝－x2＋2x＋3，BF＝OF＋OB＝x＋1；……（5 分） ∵BF＝2MF，∴x＋1＝2(－x2＋2x＋3)，化简，得：2x2－3x－5＝0 解得：x1＝－1(舍去)、x2＝5 2 ∴M(5 2 ，7 4)、N(3 2 ，15 4 )．………………………………… （7 分） ③设⊙Q 与直线 CD 的切点为 G，连接 QG，过 C 作 CH⊥QD 于 H，如下图； ∵C(0，3)、D(1，4)，∴CH＝DH＝1，即△CHD 是等腰直角三角形， ∴△QGD 也是等腰直角三角形，即：QD2＝2QG2；…………………………………… （8 分） 设 Q(1，b)，则 QD＝4－b，QG2＝QB2＝b2＋4； 得：(4－b)2＝2(b2＋4)，化简，得：b2＋8b－8＝0， 解得：b＝－4±2 6； 即点 Q 的坐标为(1，－4＋2 6)或(1，－4－2 6)．……………………………………（10 分） 中考数学试卷 一、选择题（本大题共 10 小题，每小题 3 分，共 30 分） 1．﹣5 的倒数是（ ） A． B．±5 C．5 D．﹣ 2．函数 y= 中自变量 x 的取值范围是（ ） A．x≠2 B．x≥2 C．x≤2 D．x＞2 3．下列运算正确的是（ ） A．（a2）3=a5 B．（ab）2=ab2 C．a6÷a3=a2 D．a2•a3=a5 4．下列图形中，是中心对称图形的是（ ） A． B． C． D． 5．若 a﹣b=2，b﹣c=﹣3，则 a﹣c 等于（ ） A．1 B．﹣1 C．5 D．﹣5 6．“表 1”为初三（1）班全部 43 名同学某次数学测验成绩的统计结果，则下 列说法正确的是（ ） 成绩（分） 70 80 90 男生（人） 5 10 7 女生（人） 4 13 4 A．男生的平均成绩大于女生的平均成绩 B．男生的平均成绩小于女生的平均成绩 C．男生成绩的中位数大于女生成绩的中位数 D．男生成绩的中位数小于女生成绩的中位数 7．某商店今年 1 月份的销售额是 2 万元，3 月份的销售额是 4.5 万元，从 1 月 份到 3 月份，该店销售额平均每月的增长率是（ ） A．20% B．25% C．50% D．62.5% 8．对于命题“若 a2＞b2，则 a＞b”，下面四组关于 a，b 的值中，能说明这个命 题是假命题的是（ ） A．a=3，b=2 B．a=﹣3，b=2 C．a=3，b=﹣1 D．a=﹣1，b=3 9．如图，菱形 ABCD 的边 AB=20，面积为 320，∠BAD＜90°，⊙O 与边 AB，AD 都 相切，AO=10，则⊙O 的半径长等于（ ） A．5 B．6 C．2 D．3 10．如图，△ABC 中，∠BAC=90°，AB=3，AC=4，点 D 是 BC 的中点，将△ABD 沿 AD 翻折得到△AED，连 CE，则线段 CE 的长等于（ ） A．2 B． C． D． 二、填空题（本大题共 8 小题，每小题 2 分，共 16 分） 11．计算 × 的值是 ． 12．分解因式：3a2﹣6a+3= ． 13．贵州 FAST 望远镜是目前世界第一大单口径射电望远镜，反射面总面积约 250000m2，这个数据用科学记数法可表示为 ． 14．如图是我市某连续 7 天的最高气温与最低气温的变化图，根据图中信息可知， 这 7 天中最大的日温差是 ℃． 15．若反比例函数 y= 的图象经过点（﹣1，﹣2），则 k 的值为 ． 16．若圆锥的底面半径为 3cm，母线长是 5cm，则它的侧面展开图的面积为 cm2． 17．如图，已知矩形 ABCD 中，AB=3，AD=2，分别以边 AD，BC 为直径在矩形 ABCD 的内部作半圆 O1 和半圆 O2，一平行于 AB 的直线 EF 与这两个半圆分别交于点 E、 点 F，且 EF=2（EF 与 AB 在圆心 O1 和 O2 的同侧），则由 ，EF， ，AB 所围成图 形（图中阴影部分）的面积等于 ． 18．在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A，B，C，D 都在格点处，AB 与 CD 相交于 O，则 tan∠BOD 的值等于 ． 三、解答题（本大题共 10 小题，共 84 分） 19．计算： （1）|﹣6|+（﹣2）3+（ ）0； （2）（a+b）（a﹣b）﹣a（a﹣b） 20．（1）解不等式组： （2）解方程： = ． 21．已知，如图，平行四边形 ABCD 中，E 是 BC 边的中点，连 DE 并延长交 AB 的 延长线于点 F，求证：AB=BF． 22．甲、乙、丙、丁四人玩扑克牌游戏，他们先取出两张红心和两张黑桃共四张 扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色的即为 游戏搭档，现甲、乙两人各抽取了一张，求两人恰好成为游戏搭档的概率．（请 用“画树状图”或“列表”等方法写出分析过程） 23．某数学学习网站为吸引更多人注册加入，举行了一个为期 5 天的推广活动， 在活动期间，加入该网站的人数变化情况如下表所示： 时间 第 1 天 第 2 天 第 3 天 第 4 天 第 5 天 新加入人数（人） 153 550 653 b 725 累计总人数（人） 3353 3903 a 5156 5881 （1）表格中 a= ，b= ； （2）请把下面的条形统计图补充完整； （3）根据以上信息，下列说法正确的是 （只要填写正确说法前的序号）． ①在活动之前，该网站已有 3200 人加入； ②在活动期间，每天新加入人数逐天递增； ③在活动期间，该网站新加入的总人数为 2528 人． 24．如图，已知等边△ABC，请用直尺（不带刻度）和圆规，按下列要求作图（不 要求写作法，但要保留作图痕迹）： （1）作△ABC 的外心 O； （2）设 D 是 AB 边上一点，在图中作出一个正六边形 DEFGHI，使点 F，点 H 分别 在边 BC 和 AC 上． 25．操作：“如图 1，P 是平面直角坐标系中一点（x 轴上的点除外），过点 P 作 PC⊥x 轴于点 C，点 C 绕点 P 逆时针旋转 60°得到点 Q．”我们将此由点 P 得到点 Q 的操作称为点的 T 变换． （1）点 P（a，b）经过 T 变换后得到的点 Q 的坐标为 ；若点 M 经过 T 变 换后得到点 N（6，﹣ ），则点 M 的坐标为 ． （2）A 是函数 y= x 图象上异于原点 O 的任意一点，经过 T 变换后得到点 B． ①求经过点 O，点 B 的直线的函数表达式； ②如图 2，直线 AB 交 y 轴于点 D，求△OAB 的面积与△OAD 的面积之比． 26．某地新建的一个企业，每月将生产 1960 吨污水，为保护环境，该企业计划 购置污水处理器，并在如下两个型号种选择： 污水处理器型号 A 型 B 型 处理污水能力（吨/月） 240 180 已知商家售出的 2 台 A 型、3 台 B 型污水处理器的总价为 44 万元，售出的 1 台 A 型、4 台 B 型污水处理器的总价为 42 万元． （1）求每台 A 型、B 型污水处理器的价格； （2）为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器， 那么他们至少要支付多少钱？ 27．如图，以原点 O 为圆心，3 为半径的圆与 x 轴分别交于 A，B 两点（点 B 在 点 A 的右边），P 是半径 OB 上一点，过 P 且垂直于 AB 的直线与⊙O 分别交于 C， D 两点（点 C 在点 D 的上方），直线 AC，DB 交于点 E．若 AC：CE=1：2． （1）求点 P 的坐标； （2）求过点 A 和点 E，且顶点在直线 CD 上的抛物线的函数表达式． 28．如图，已知矩形 ABCD 中，AB=4，AD=m，动点 P 从点 D 出发，在边 DA 上以每 秒 1 个单位的速度向点 A 运动，连接 CP，作点 D 关于直线 PC 的对称点 E，设点 P 的运动时间为 t（s）． （1）若 m=6，求当 P，E，B 三点在同一直线上时对应的 t 的值． （2）已知 m 满足：在动点 P 从点 D 到点 A 的整个运动过程中，有且只有一个时 刻 t，使点 E 到直线 BC 的距离等于 3，求所有这样的 m 的取值范围． 参考答案与试题解析 一、选择题（本大题共 10 小题，每小题 3 分，共 30 分） 1．﹣5 的倒数是（ ） A． B．±5 C．5 D．﹣ 【考点】17：倒数． 【分析】根据倒数的定义，即可求出﹣5 的倒数． 【解答】解：∵﹣5×（﹣ ）=1， ∴﹣5 的倒数是﹣ ． 故选 D． 2．函数 y= 中自变量 x 的取值范围是（ ） A．x≠2 B．x≥2 C．x≤2 D．x＞2 【考点】E4：函数自变量的取值范围． 【分析】根据分式的意义的条件，分母不等于 0，可以求出 x 的范围．x k b 1 . c o m 【解答】解：根据题意得：2﹣x≠0， 解得：x≠2． 故函数 y= 中自变量 x 的取值范围是 x≠2． 故选 A． 3．下列运算正确的是（ ） A．（a2）3=a5 B．（ab）2=ab2 C．a6÷a3=a2 D．a2•a3=a5 【考点】48：同底数幂的除法；46：同底数幂的乘法；47：幂的乘方与积的乘方． 【分析】利用幂的运算性质直接计算后即可确定正确的选项． 【解答】解：A、（a2）3=a6，故错误，不符合题意； B、（ab）2=a2b2，故错误，不符合题意； C、a6÷a3=a3，故错误，不符合题意； D、a2•a3=a5，正确，符合题意， 故选 D． 4．下列图形中，是中心对称图形的是（ ） A． B． C． D． 【考点】R5：中心对称图形． 【分析】根据中心对称图形的定义逐个判断即可． 【解答】解：A、不是中心对称图形，故本选项不符合题意； B、不是中心对称图形，故本选项不符合题意；w w w .x k b 1.c o m C、是中心对称图形，故本选项符合题意； D、不是中心对称图形，故本选项不符合题意； 故选 C． 5．若 a﹣b=2，b﹣c=﹣3，则 a﹣c 等于（ ） A．1 B．﹣1 C．5 D．﹣5 【考点】44：整式的加减． 【分析】根据题中等式确定出所求即可． 【解答】解：∵a﹣b=2，b﹣c=﹣3， ∴a﹣c=（a﹣b）+（b﹣c）=2﹣3=﹣1， 故选 B 6．“表 1”为初三（1）班全部 43 名同学某次数学测验成绩的统计结果，则下 列说法正确的是（ ） 成绩（分） 70 80 90 男生（人） 5 10 7 女生（人） 4 13 4 A．男生的平均成绩大于女生的平均成绩 B．男生的平均成绩小于女生的平均成绩 C．男生成绩的中位数大于女生成绩的中位数 D．男生成绩的中位数小于女生成绩的中位数 【考点】W4：中位数；W1：算术平均数． 【分析】根据平均数的定义分别求出男生与女生的平均成绩，再根据中位数的定 义分别求出男生与女生成绩的中位数即可求解． 【解答】解：∵男生的平均成绩是：（70×5+80×10+90×7）÷22=1780÷22=80 ， 女生的平均成绩是：（70×4+80×13+90×4）÷21=1680÷21=80， ∴男生的平均成绩大于女生的平均成绩． ∵男生一共 22 人，位于中间的两个数都是 80，所以中位数是（80+80）÷2=80， 女生一共 21 人，位于最中间的一个数是 80，所以中位数是 80， ∴男生成绩的中位数等于女生成绩的中位数． 故选 A． 7．某商店今年 1 月份的销售额是 2 万元，3 月份的销售额是 4.5 万元，从 1 月 份到 3 月份，该店销售额平均每月的增长率是（ ） A．20% B．25% C．50% D．62.5% 【考点】AD：一元 二次方程的应用． 【分析】设每月增长率为 x，据题意可知：三月份销售额为 2（1+x）2 万元，依 此等量关系列出方程，求解即可． 【解答】解：设该店销售额平均每月的增长率为 x，则二月份销售额为 2（1+x） 万元，三月份销售额为 2（1+x）2 万元， 由题意可得：2（1+x）2=4.5， 解得：x1=0.5=50%，x2=﹣2.5（不合题意舍去）， 答即该店销售额平均每月的增长率为 50%； 故选：C． 8．对于命题“若 a2＞b2，则 a＞b”，下面四组关于 a，b 的值中，能说明这个命 题是假命题的是（ ） A．a=3，b=2 B．a=﹣3，b=2 C．a=3，b=﹣1 D．a=﹣1，b=3 【考点】O1：命题与定理． 【分析】说明命题为假命题，即 a、b 的值满足 a2＞b2，但 a＞b 不成立，把四个 选项中的 a、b 的值分别难度验证即可． 【解答】解： 在 A 中，a2=9，b2=4，且 3＞2，满足“若 a2＞b2，则 a＞b”，故 A 选项中 a、b 的值不能说明命题为假命题； 在 B 中，a2=9，b2=4，且﹣3＜2，此时虽然满足 a2＞b2，但 a＞b 不成立，故 B 选 项中 a、b 的值可以说明命题为假命题； 在 C 中，a2=9，b2=1，且 3＞﹣1，满足“若 a2＞b2，则 a＞b”，故 C 选项中 a、b 的值不能说明命题为假命题； 在 D 中，a2=1，b2=9，且﹣1＜3，此时满足 a2＜b2，得出 a＜b，即意味着命题“若 a2＞b2，则 a＞b”成立，故 D 选项中 a、b 的值不能说明命题为假命题； 故选 B．w w w .x k b 1.c o m 9．如图，菱形 ABCD 的边 AB=20，面积为 320，∠BAD＜90°，⊙O 与边 AB，AD 都 相切，AO=10，则⊙O 的半径长等于（ ） A．5 B．6 C．2 D．3 【考点】MC：切线的性质；L8：菱形的性质． 【分析】如图作 DH⊥AB 于 H，连接 BD，延长 AO 交 BD 于 E．利用菱形的面积公 式求出 DH，再利用勾股定理求出 AH，BD，由△AOF∽△DBH，可得 = ，延长 即可解决问题． 【解答】解：如图作 DH⊥AB 于 H，连接 BD，延长 AO 交 BD 于 E． ∵菱形 ABCD 的边 AB=20，面积为 320， ∴AB•DH=32O， ∴DH=16， 在 Rt△ADH 中，AH= =12， ∴HB=AB﹣AH=8， 在 Rt△BDH 中，BD= =8 ， 设⊙O 与 AB 相切于 F，连接 AF． ∵AD=AB，OA 平分∠DAB， ∴AE⊥BD， ∵∠OAF+∠ABE=90°，∠ABE+∠BDH=90°， ∴∠OAF=∠BDH，∵∠AFO=∠DHB=90°， ∴△AOF∽△DBH， ∴ = ， ∴ = ， ∴OF=2 ． 故选 C． 10．如图，△ABC 中，∠BAC=90°，AB=3，AC=4，点 D 是 BC 的中点，将△ABD 沿 AD 翻折得到△AED，连 CE，则线段 CE 的长等于（ ） A．2 B． C． D． 【考点】PB：翻折变换（折叠问题）；KP：直角三角形斜边上的中线；KQ：勾股 定理． 【分析】如图连接 BE 交 AD 于 O，作 AH⊥BC 于 H．首先证明 AD 垂直平分线段 BE， △BCE 是直角三角形，求出 BC、BE 在 Rt△BCE 中，利用勾股定理即可解决问题． 【解答】解：如图连接 BE 交 AD 于 O，作 AH⊥BC 于 H． 在 Rt△ABC 中，∵AC=4，AB=3， ∴BC= =5， ∵CD=DB， ∴AD=DC=DB= ， ∵ •BC•AH= •AB•AC， ∴AH= ， ∵AE=AB，DE=DB=DC， ∴AD 垂直平分线段 BE，△BCE 是直角三角形， ∵ •AD•BO= •BD•AH， ∴OB= ， ∴BE=2OB= ， 在 Rt△BCE 中，EC= = = ， 故选 D． 二、填空题（本大题共 8 小题，每小题 2 分，共 16 分） 11．计算 × 的值是 6 ． 【考点】75：二次根式的乘除法． 【分析】根据 • = （a≥0，b≥0）进行计算即可得出答案． 【解答】解： × = = =6； 故答案为：6． 12．分解因式：3a2﹣6a+3= 3（a﹣1）2 ． 【考点】55：提公因式法与公式法的综合运用． 【分析】首先提取公因式 3，进而利用完全平方公式分解因式得出答案． 【解答】解：原式=3（a2﹣2a+1）=3（a﹣1）2． 故答案为：3（a﹣1）2． 13．贵州 FA ST 望远镜是目前世界第一大单口径射电望远镜，反射面总面积约 250000m2，这个数据用科学记数法可表示为 2.5×105 ． 【考点】1I：科学记数法—表示较大的数． 【分析】科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确 定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点 移动的位数相同．当原数绝对值＞1 时，n 是正数；当原数的绝对值＜1 时，n 是负数． 【解答】解：将 250000 用科学记数法表示为：2.5×105． 故答案为：2.5×105． 14．如图是我市某连续 7 天的最高气温与最低气温的变化图，根据图中信息可知， 这 7 天中最大的日温差是 11 ℃． 【考点】18：有理数大小比较；1A：有理数的减法． 【分析】求出每天的最高气温与最低气温的差，再比较大小即可． 【解答】解：∵由折线统计图可知，周一的日温差=8℃+1℃=9℃；周二的日温差 =7℃+1℃=8℃；周三的日温差=8℃+1℃=9℃；周四的日温差=9℃；周五的日温差 =13℃﹣5℃=8℃；周六的日温差=15℃﹣71℃=8℃；周日的日温差=16℃﹣ 5℃=11℃， ∴这 7 天中最大的日温差是 11℃． 故答案为：11． 15．若反比例函数 y= 的图象经过点（﹣1，﹣2），则 k 的值为 2 ． 【考点】G7：待定系数法求反比例函数解析式． 【分析】由一个已知点来求反比例函数解析式，只要把已知点的坐标代入解析式 就可求出比例系数． 【解答】解：把点（﹣1，﹣2）代入解析式可得 k=2． 16．若圆锥的底面半径为 3cm，母线长是 5cm，则它的侧面展开图的面积为 15π cm2． 【考点】MP：圆锥的计算． 【分析】圆锥的侧面积=底面周长×母线长÷2． 【解答】解：底面半径为 3cm，则底面周长=6πcm，侧面面积= ×6π×5=15πcm2． 17．如图，已知矩形 ABCD 中，AB=3，AD=2，分别以边 AD，BC 为直径在矩形 ABCD 的内部作半圆 O1 和半圆 O2，一平行于 AB 的直线 EF 与这两个半圆分别交于点 E、 点 F，且 EF=2（EF 与 AB 在圆心 O1 和 O2 的同侧），则由 ，EF， ，AB 所围成图 形（图中阴影部分）的面积等于 3﹣ ﹣ ． 【考点】MO：扇形面积的计算；LB：矩形的性质． 【分析】连接 O1O2，O1E，O2F，过 E 作 EG⊥O1O2，过 F⊥O1O2，得到四边形 EGHF 是 矩形，根据矩形的性质得到 GH=EF=2，求得 O1G= ，得到∠O1EG=30°，根据三角 形、梯形、扇形的面积公式即可得到结论． 【解答】解：连接 O1O2，O1E，O2F， 则四边形 O1O2FE 是等腰梯形， 过 E 作 EG⊥O1O2，过 F⊥O1O2， ∴四边形 EGHF 是矩形， ∴GH=EF=2， ∴O1G= ， ∵O1E=1， ∴GE= ， ∴ = ； ∴∠O1EG=30°， ∴∠AO1E=30°， 同理∠BO2F=30°， ∴ 阴 影 部 分 的 面 积 =S ﹣ 2S ﹣ S =3 × 1 ﹣ 2 × ﹣ （2+3）× =3﹣ ﹣ ． 故答案为：3﹣ ﹣ ． 18．在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A，B，C，D 都在格点处，AB 与 CD 相交于 O，则 tan∠BOD 的值等于 3 ． 【考点】T7：解直角三角形． 【分析】根据平移的性质和锐角三角函数以及勾股定理，通过转化的数学思想可 以求得 tan∠BOD 的值．，本题得以解决 【解答】解：平移 CD 到 C′D′交 AB 于 O′，如右图所示， 则∠BO′D′=∠BOD， ∴tan∠BOD=tan∠BO′D′， 设每个小正方形的边长为 a， 则 O′B= ，O′D′= ，BD′=3a， 作 BE⊥O′D′于点 E， 则 BE= ， ∴O′E= = ， ∴tanBO′E= ， ∴tan∠BOD=3， 故答案为：3． 三、解答题（本大题共 10 小题，共 84 分） 19．计算： （1）|﹣6|+（﹣2）3+（ ）0； （2）（a+b）（a﹣b）﹣a（a﹣b） 【考点】4F：平方差公式；2C：实数的运算；4A：单项式乘多项式；6E：零指数 幂． 【分析】（1）根据零指数幂的意义以及绝对值的意义即可求出答案； （2）根据平方差公式以及单项式乘以多项式法则即可求出答案． 【解答】解：（1）原式=6﹣8+1=﹣1 （2）原式=a2﹣b2﹣a2+ab=ab﹣b2 20．（1）解不等式组： （2）解方程： = ． 【考点】B3：解分式方程；CB：解一元一次不等式组． 【分析】（1）分别解不等式，进而得出不等式组的解集； （2）直接利用分式的性质求出 x 的值，进而得出答案． 【解答】解：（1）解①得：x＞﹣1，新$课$标$第$一$网 解②得：x≤6， 故不等式组的解集为：﹣1＜x≤6； （2）由题意可得：5（x+2）=3（2x﹣1）， 解得：x=13， 检验：当 x=13 时，（x+2）≠0，2x﹣1≠0， 故 x=13 是原方程的解． 21．已知，如图，平行四边形 ABCD 中，E 是 BC 边的中点，连 DE 并延长交 AB 的 延长线于点 F，求证：AB=BF． 【考点】L5：平行四边形的性质；KD：全等三角形的判定与性质． 【分析】根据线段中点的定义可得 CE=BE，根据平行四边形的对边平行且相等可 得 AB∥CD，AB=CD，再根据两直线平行，内错角相等可得∠DCB=∠FBE，然后利 用“角边角”证明△CED 和△BEF 全等，根据全等三角形对应边相等可得 CD=BF， 从而得证． 【解答】证明：∵E 是 BC 的中点， ∴CE=BE， ∵四边形 ABCD 是平行四边形， ∴AB∥CD，AB=CD， ∴∠DCB=∠FBE， 在△CED 和△BEF 中， ， ∴△CED≌△BEF（ASA）， ∴CD=BF， ∴AB=BF． 22．甲、乙、丙、丁四人玩扑克牌游戏，他们先取出两张红心和两张黑桃共四张 扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色的即为 游戏搭档，现甲、乙两人各抽取了一张，求两人恰好成为游戏搭档的概率．（请 用“画树状图”或“列表”等方法写出分析过程） 【考点】X6：列表法与树状图法． 【分析】利用列举法即可列举出所有各种可能的情况，然后利用概率公式即可求 解． 【解答】解：根据题意画图如下： 共有 12 中情况，从 4 张牌中任意摸出 2 张牌花色相同颜色 4 种可能，所以两人 恰好成为游戏搭档的概率= = ． 23．某数学学习网站为吸引更多人注册加入，举行了一个为期 5 天的推广活动， 在活动期间，加入该网站的人数变化情况如下表所示： 时间 第 1 天 第 2 天 第 3 天 第 4 天 第 5 天 新加入人数（人） 153 550 653 b 725 累计总人数（人） 3353 3903 a 5156 5881 （1）表格中 a= 4556 ，b= 600 ； （2）请把下面的条形统计图补充完整； （3）根据以上信息，下列说法正确的是 ① （只要填写正确说法前的序号）． ①在活动之前，该网站已有 3200 人加入； ②在活动期间，每天新加入人数逐天递增； ③在活动期间，该网站新加入的总人数为 2528 人． 【考点】VC：条形统计图． 【分析】（1）观察表格中的数据即可解决问题； （2）根据第 4 天的人数 600，画出条形图即可； （3）根据题意一一判断即可； 【解答】解：（1）由题意 a=3903+653=4556，b=5156﹣4556=600． 故答案为 4556，600． （2）统计图如图所示， （3）①正确．3353﹣153=3200．故正确． ②错误．第 4 天增加的人数 600＜第 3 天 653，故错误． ③错误．增加的人数=153+550+653+600+725=2681，故错误． 故答案为① 24．如图，已知等边△ABC，请用直尺（不带刻度）和圆规，按下列要求作图（不 要求写作法，但要保留作图痕迹）： （1）作△ABC 的外心 O； （2）设 D 是 AB 边上一点，在图中作出一个正六边形 DEFGHI，使点 F，点 H 分别 在边 BC 和 AC 上． 【考点】N3：作图—复杂作图；KK：等边三角形的性质；MA：三角形的外接圆与 外心． 【分析】（1）根据垂直平分线的作法作出 AB，AC 的垂直平分线交于点 O 即为所 求； （2）过 D 点作 DI∥BC 交 AC 于 I，分别以 D，I 为圆心，DI 长为半径作圆弧交 AB 于 E，交 AC 于 H，过 E 点作 EF∥AC 交 BC 于 F，过 H 点作 HG∥AB 交 BC 于 G， 六边形 DEFGHI 即为所求正六边形． 【解答】解：（1）如图所示：点 O 即为所求． （2）如图所示：六边形 DEFGHI 即为所求正六边形． 25．操作：“如图 1，P 是平面直角坐标系中一点（x 轴上的点除外），过点 P 作 PC⊥x 轴于点 C，点 C 绕点 P 逆时针旋转 60°得到点 Q．”我们将此由点 P 得到点 Q 的操作称为点的 T 变换． （1）点 P（a，b）经过 T 变换后得到的点 Q 的坐标为 （a+ b， b） ；若 点 M 经过 T 变换后得到点 N（6，﹣ ），则点 M 的坐标为 （9，﹣2 ） ． （2）A 是函数 y= x 图象上异于原点 O 的任意一点，经过 T 变换后得到点 B． ①求经过点 O，点 B 的直线的函数表达式； ②如图 2，直线 AB 交 y 轴于点 D，求△OAB 的面积与△OAD 的面积之比． 【考点】FI：一次函数综合题． 【分析】（1）连接 CQ 可知△PCQ 为等边三角形，过 Q 作 QD⊥PC，利用等边三角 形的性质可求得 CD 和 QD 的长，则可求得 Q 点坐标；设出 M 点的坐标，利用 P、 Q 坐标之间的关系可得到点 M 的方程，可求得 M 点的坐标； （2）①可取 A（2， ），利用 T 变换可求得 B 点坐标，利用待定系数示可求得 直线 OB 的函数表达式；②由待定系数示可求得直线 AB 的解析式，可求得 D 点坐 标，则可求得 AB、AD 的长，可求得△OAB 的面积与△OAD 的面积之比． 【解答】解： （1）如图 1，连接 CQ，过 Q 作 QD⊥PC 于点 D， 由旋转的性质可得 PC=PQ，且∠CPQ=60°， ∴△PCQ 为等边三角形， ∵P（a，b）， ∴OC=a，PC=b， ∴CD= PC= b，DQ= PQ= b， ∴Q（a+ b， b）； 设 M（x，y），则 N 点坐标为（x+ y， y）， ∵N（6，﹣ ）， ∴ ，解得 ， ∴M（9，﹣2 ）； 故答案为：（a+ b， b）；（9，﹣2 ）； （2）①∵A 是函数 y= x 图象上异于原点 O 的任意一点， ∴可取 A（2， ）， ∴2+ × = ， × = ， ∴B（ ， ）， 设直线 OB 的函数表达式为 y=kx，则 k= ，解得 k= ， ∴直线 OB 的函数表达式为 y= x； ②设直线 AB 解析式为 y=k′x+b， 把 A、B 坐标代入可得 ，解得 ， ∴直线 AB 解析式为 y=﹣ x+ ， ∴D（0， ），且 A（2， ），B（ ， ）， ∴AB= = ，AD= = ， ∴ = = = ． 26．某地新建的一个企业，每月将生产 1960 吨污水，为保护环境，该企业计划 购置污水处理器，并在如下两个型号种选择： 污水处理器型号 A 型 B 型 处理污水能力（吨/月） 240 180 已知商家售出的 2 台 A 型、3 台 B 型污水处理器的总价为 44 万元，售出的 1 台 A 型、4 台 B 型污水处理器的总价为 42 万元． （1）求每台 A 型、B 型污水处理器的价格； （2）为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器， 那么他们至少要支付多少钱？ 【考点】C9：一元一次不等式的应用；9A：二元一次方程组的应用． 【分析】（1）可设每台 A 型污水处理器的价格是 x 万元，每台 B 型污水处理器的 价格是 y 万元，根据等量关系：①2 台 A 型、3 台 B 型污水处理器的总价为 44 万元，②1 台 A 型、4 台 B 型污水处理器的总价为 42 万元，列出方程组求解即 可； （2）由于求至少要支付的钱数，可知购买 6 台 A 型污水处理器、3 台 B 型污水 处理器，费用最少，进而求解即可． 【解答】解：（1）可设每台 A 型污水处理器的价格是 x 万元，每台 B 型污水处理 器的价格是 y 万元，依题意有 ， 解得 ． 答：设每台 A 型污水处理器的价格是 10 万元，每台 B 型污水处理器的价格是 8 万元； （2）购买 6 台 A 型污水处理器、3 台 B 型污水处理器，费用最少， 10×6+8×3 =60+24 =84（万元）． 答：他们至少要支付 84 万元钱． 27．如图，以原点 O 为圆心，3 为半径的圆与 x 轴分别交于 A，B 两点（点 B 在 点 A 的右边），P 是半径 OB 上一点，过 P 且垂直于 AB 的直线与⊙O 分别交于 C， D 两点（点 C 在点 D 的上方），直线 AC，DB 交于点 E．若 AC：CE=1：2． （1）求点 P 的坐标； （2）求过点 A 和点 E，且顶点在直线 CD 上的抛物线的函数表达式． 【考点】MR：圆的综合题． 【分析】（1）如图，作 EF⊥y 轴于 F，DC 的延长线交 EF 于 H．设 H（m，n），则 P（m，0），PA=m+3，PB=3﹣m．首先证明△ACP∽△ECH，推出 = = = ，推 出 CH=2n，EH=2m=6，再证明△DPB∽△DHE，推出 = = = ，可得 = ， 求出 m 即可解决问题； （2）由题意设抛 物线的解析式为 y=a（x+3）（x﹣5），求出 E 点坐标代入即可解 决问题； 【解答】解：（1）如图，作 EF⊥y 轴于 F，DC 的延长线交 EF 于 H．设 H（m，n）， 则 P（m，0），PA=m+3，PB=3﹣m． ∵EH∥AP， ∴△ACP∽△ECH， ∴ = = = ， ∴CH=2n，EH=2m=6， ∵CD⊥AB， ∴PC=PD=n， ∵PB∥HE， ∴△DPB∽△DHE， ∴ = = = ， ∴ = ， ∴m=1， ∴P（1，0）．[来源:学§科§网] （2）由（1）可知，PA=4，HE=8，EF=9， 连接 OP，在 Rt△OCP 中，PC= =2 ， ∴CH=2PC=4 ，PH=6 ， ∴E（9，6 ）， ∵抛物线的对称轴为 CD， ∴（﹣3，0）和（5，0）在抛物线上，设抛物线的解析式为 y=a（x+3）（x﹣5）， 把 E（9，6 ）代入得到 a= ， ∴抛物线的解析式为 y= （x+3）（x﹣5），即 y= x2﹣ x﹣ ． 28．如图，已知矩形 ABCD 中，AB=4，AD=m，动点 P 从点 D 出发，在边 DA 上以每 秒 1 个单位的速度向点 A 运动，连接 CP，作点 D 关于直线 PC 的对称点 E，设点 P 的运动时间为 t（s）． （1）若 m=6，求当 P，E，B 三点在同一直线上时对应的 t 的值． （2）已知 m 满足：在动点 P 从点 D 到点 A 的整个运动过程中，有且只有一个时 刻 t，使点 E 到直线 BC 的距离等于 3，求所有这样的 m 的取值范围． 【考点】LO：四边形综合题． 【分析】（1）只要证明△ABD∽△DPC，可得 = ，由此求出 PD 即可解决问题； （2）分两种情形求出 AD 的值即可解决问题：①如图 2 中，当点 P 与 A 重合时， 点 E 在 BC 的下方，点 E 到 BC 的距离为 3．②如图 3 中，当点 P 与 A 重合时，点 E 在 BC 的上方，点 E 到 BC 的距离为 3； 【解答】解：（1）如图 1 中， ∵四边形 ABCD 是矩形， ∴∠ADC=∠A=90°， ∴∠DCP+∠CPD=90°， ∵∠CPD+∠ADB=90°， ∴∠ADB=∠PCD， ∵∠A=∠CDP=90°， ∴△ABD∽△DPC， ∴ = ， ∴ = ， ∴PD= ， ∴t= s 时，B、E、D 共线． （2）如图 2 中，当点 P 与 A 重合时，点 E 在 BC 的下方，点 E 到 BC 的距离为 3． 作 EQ⊥BC 于 Q，EM⊥DC 于 M．则 EQ=3，CE=DC=4 易证四边形 EMCQ 是矩形， ∴CM=EQ=3，∠M=90°， ∴EM= = = ， ∵∠DAC=∠EDM，∠ADC=∠M， ∴△ADC∽△DME， = ， ∴ = ， ∴AD=4 ， 如图 3 中，当点 P 与 A 重合时，点 E 在 BC 的上方，点 E 到 BC 的距离为 3． 作 EQ⊥BC 于 Q，延长 QE 交 AD 于 M．则 EQ=3，CE=DC=4 在 Rt△ECQ 中，QC=DM= = ， 由△DME∽△CDA， ∴ = ， ∴ = ， ∴AD= ， 综上所述，在动点 P 从点 D 到点 A 的整个运动过程中，有且只有一个时刻 t，使 点 E 到直线 BC 的距离等于 3，这样的 m 的取值范围 ≤m＜4 ． 中考数学试题 亲爱的同学，在你答题前，请认真阅读下面以及“答卷”上的注意事项： 1．本试卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分组成．全卷共 6 页，三大题，满 分 l20 分．考试用时 120 分钟．矚慫润厲钐瘗睞枥庑赖。 2．答题前，请将你的姓名、准考证号填写在“答卷”相应位置，并在“答卷”背面左 上角填写姓名和准考证号后两位．聞創沟燴鐺險爱氇谴净。 3．答第Ⅰ卷(选择题)时，选出每小题答案后，用 2B 铅笔把“答卷”上对应题目的答案 标号涂黑．如需改动，用橡皮擦干净后。再选涂其他答案．不得答在“试卷”上．残骛楼諍锩 瀨濟溆塹籟。 4．第Ⅱ卷(非选择题)用 0.5 毫米黑色笔迹签字笔书写在“答卷”上，答在“试卷”上无 效． 预祝你取得优异成绩! 第Ⅰ卷（选择题，共 36 分） 一、选择题（共 12 小题。每小题 3 分。共 36 分） 下列各题中均有四个备选答案，其中有且只有一个正确，请在答卷上将正确答案的代号涂黑． 1．有理数－2 的相反数是（） （A）2 （B）－2 （C） 1 2 （D）－ 1 2 2．函数 1y x  中自变量 x 的取值范围是（） (A)x≥1．(B)x≥－1． (C)x≤1．(D)x≤－1． 3．如图，数轴上表示的是某不等式组的解集，则这个不等式组可能是（） （A）x＞－1，x＞2 （B）x＞－1，x＜2 （C）x＜－1，x＜2 （D）x＜－1，x＞2 4．下列说法：①“掷一枚质地均匀的硬币一定是正面朝上”；②“从一副普通扑克牌中任意 抽取一张，点数一定是 6”．酽锕极額閉镇桧猪訣锥。 (A)①②都正确．(B)只有①正确．(C)只有②正确．(D)①②都正确． 5．2010 年上海世博会开园第一个月共售出门票 664 万张，664 万用科学计数法表示为( ) (A)664×104 (B)66.4×l05 (C)6.64×106 (D)0.664×l07 彈贸摄尔霁毙攬砖卤庑。 6．如图，△ABC 内有一点 D，且 DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC 的大小是（）謀荞抟箧飆鐸怼类蒋薔。 (A)100° (B)80° (C)70° (D)50° 7．若 x1，x2 是方程 x2=4 的两根，则 x1+x2 的值是( ) (A)8．(B)4． (C)2．(D)0． 8．如图所示，李老师办公桌上放着一个圆柱形茶叶盒 和一个正方体的墨水盒，小芳从上面看，看到的图 形是 (A) (B) (C) (D) 9．如图，所有正方形的中心均在坐标原点，且各边与 x 轴或 y 轴平行．从内到外，它们的 边长依次为 2，4，6，8，…，顶点依次用 A1，A2，A3，A4，…表示，则顶点 A55 的坐 标是（）厦礴恳蹒骈時盡继價骚。 (A)（13，13） (B)（―13，―13） (C)（14，14） (D)（－14，－14）茕桢广 鳓鯡选块网羈泪。 10．如图，⊙O 的直径 AB 的长为 10，弦 AC 长为 6，∠AC'B 的平分线交⊙O 于 D，则 CD 长为（） (A) 7 (B) 7 2 (C) 8 2 (D) 9 11．随着经济的发展，人们的生活水平不断提高．下图分别是某景点 2007—2009 年游客总 人数和旅游收入年增长率统计图．已知该景点 2008 年旅游收入 4500 万元．鹅娅尽損鹌惨 歷茏鴛賴。 下列说法：①三年中该景点 2009 年旅游收入最高；②与 2007 年相比，该景点 2009 年的旅游收入增加[4500×(1+29%)－4500×(1－33%)]万元；③若按 2009 年游客人数的 年增长率计算，2010 年该景点游客总人数将达到 280 255280 (1 )255   万人次。其中正 确的个数是（）籟丛妈羥为贍偾蛏练淨。 (A)0 (B)1 (C)2 (D)3 12．如图，在直角梯形 ABCD 中，AD∥BC，∠ABC=90°，BD⊥DC，BE=DC，CE 平分 ∠BCD，交 AB 于点 E，交 BD 于点 H，EN∥DC 交 BD 于点 N．下列结论：預頌圣鉉儐 歲龈讶骅籴。 ①BH=DH；②CH= ( 2 1)EH ；③ ENH EBH S EH S EC   ． H N E C A D B 其中正确的是（） (A)①②③ (B)只有②③ (C)只有② (D)只有③ 第Ⅱ卷（非选择题，共 84 分) 二、填空题（共 4 小题，每小题 3 分，共 12 分)． 下列各题不需要写出解答过程，请将结果宣接填写在答卷指定的位置． 13．计算：sin30°=_________，(－3a2) 2=_________， 2( 5) =_________．渗釤呛俨匀谔鱉调 硯錦。 14．某校八年级(2)班四名女生的体重(单位：kg)分别是：35，36，38，40．这组数据的中位 数是_________．铙誅卧泻噦圣骋贶頂廡。 15．如图，直线 y1=kx+b 过点 A（0，2），且与直线 y2=mx 交于点 P（1，m），则不等式组 mx＞kx+b＞mx－2 的解集是______________. （第 15 题图）（第 16 题图） 16．如图，直线 3 3y x b   与 y 轴交于点 A，与双曲线 ky x  在第一象限交于 B、C 两 点，且 AB·AC=4，则 k=_________．擁締凤袜备訊顎轮烂蔷。 三、解答题(共 9 小题，共 72 分) 下列各题需要在答卷指定位置写出文字说明、证明过程、演算步骤或画出图形． 17．(本题满分 6 分)解方程：x2+x－1=0． 18．(本题满分 6 分)先化简，再求值： 5 3( 2 )2 2 4 xx x x     ，其中 2 3x   ． 19．(本题满分 6 分)如图。点 B，F，C，E 在同一条直线上，点 A，D 在直线 BE 的两侧， AB∥DE，AC∥DF，BF=CE．求证：AC=DF．贓熱俣阃歲匱阊邺镓騷。 D B E A F C 20．(本题满分 7 分)小伟和小欣玩一种抽卡片游戏：将背面完全相同，正面分别写有 1，2， 3，4 的四张卡片混合后，小伟从中随机抽取一张。记下数字后放回，混合后小欣再随 机抽取一张，记下数字．如果所记的两数字之和大于 4，则小伟胜；如果所记的两数字 之和不大于 4，则小欣胜。坛摶乡囂忏蒌鍥铃氈淚。 (1)请用列表或画树形图的方法。分别求出小伟，小欣获胜的概率； (2)若小伟抽取的卡片数字是 1，问两人谁获胜的可能性大?为什么? 21．(本题满分 7 分)(1)在平面直角坐标系中，将点 A（－3，4）向右平移 5 个单位到点 A1， 再将点 A1 绕坐标原点顺时针旋转 90°到点 A2．直接写出点 A1，A2 的坐标；蜡變黲癟報 伥铉锚鈰赘。 (2)在平面直角坐标系中，将第二象限内的点 B（a，b）向右平移 m 个单位到第一象限 点 B1，再将点 B1 绕坐标原点顺时针旋转 90°到点 B2，直接写出点 B1，B2 的坐标； 買鲷鴯譖昙膚遙闫撷凄。 (3)在平面直角坐标系中。将点 P（c，d）沿水平方向平移 n 个单位到点 P1，再将点 P1 绕坐标原点顺时针旋转 90°到点 P2，直接写出点 P2 的坐标．綾镝鯛駕櫬鹕踪韦辚糴。 22．(本题满分 8 分)如图，点 O 在∠APB 的平分线上，⊙O 与 PA 相切于点 C． (1)求证：直线 PB 与⊙O 相切； (2)PO 的延长线与⊙O 交于点 E．若⊙O 的半径为 3，PC=4．求弦 CE 的长． 23．(本题满分 10 分)某宾馆有 50 个房间供游客住宿，当每个房间的房价为每天 l80 元时， 房间会全部住满．当每个房间每天的房价每增加 10 元时，就会有一个房间空闲．宾馆 需对游客居住的每个房间每天支出 20 元的各种费用．根据规定，每个房间每天的房价 不得高于 340 元．设每个房间的房价每天增加 x 元(x 为 10 的正整数倍)．驅踬髏彦浃绥譎 饴憂锦。 (1)设一天订住的房间数为 y，直接写出 y 与 x 的函数关系式及自变量 x 的取值范围； (2)设宾馆一天的利润为 w 元，求 w 与 x 的函数关系式； (3)一天订住多少个房间时，宾馆的利润最大?最大利润是多少元? 24．(本题满分 10 分)已知：线段 OA⊥OB，点 C 为 OB 中点，D 为线段 OA 上一点。连结 AC，BD 交于点 P．猫虿驢绘燈鮒诛髅貺庑。 (1)如图 1，当 OA=OB，且 D 为 OA 中点时，求 AP PC 的值； (2)如图 2，当 OA=OB，且 AD 1 AO 4  时，求 tan∠BPC 的值． (3)如图 3，当 AD∶AO∶OB=1∶n∶ 2 n 时，直接写出 tan∠BPC 的值． （图 1）（图 2）（图 3） 25．(本题满分 12 分)如图．抛物线 2 1 2y ax ax b   经过 A（－1，0），C（2， 3 2 ）两点， 与 x 轴交于另一点 B． (1)求此地物线的解析式； (2)若抛物线的顶点为 M，点 P 为线段 OB 上一动点(不与点 B 重合)，点 Q 在线段 MB 上移动，且∠MPQ=45°，设线段 OP=x，MQ= 2 2 2 y ，求 y2 与 x 的函数关系式， 并直接写出自变量 x 的取值范围；锹籁饗迳琐筆襖鸥娅薔。 (3)在同一平面直角坐标系中，两条直线 x=m，x=n 分别与抛物线交于点 E，G，与(2) 中的函数图象交于点 F，H．问四边形 EFHG 能否为平行四边形?若能，求 m，n 之 间的数量关系；若不能，请说明理由．構氽頑黉碩饨荠龈话骛。 备用图 2010 湖北武汉市中考数学解答 一、选择题： 1.A，2. A，3. B，4. D，5. C，6. A，7. D，8. A，9. C，10. B，11. C，12. B，輒峄 陽檉簖疖網儂號泶。 二、填空题 13. 2 1 ，9a4，5， 14. 37， 15. 1