2009年广东省汕头市初中毕业生学业考试 10页

‎★机密·启用前 ‎2009年广东省汕头市初中毕业生学业考试 数 学 说明:‎ ‎1.全卷共4页，考试用时100分钟，满分为150分.‎ ‎2.答题前，考生必须将自己的姓名、准考证号、学校按要求填写在答卷密封线左边的空格内；并填写答卷右上角的座位号，将姓名、准考证号用2B铅笔写、涂在答题卡指定的位置上。‎ ‎3.选择题的答题必须用2B铅笔将答题卡对应小题所选的选项涂黑．‎ ‎4．非选择题可用黑色或蓝色字迹的钢笔、签字笔按各题要求写在答卷上，不能用铅笔和红笔．写在试卷上的答案无效．姓名 ‎5．必须保持答卷的清洁．考试结束时，将试题、答卷、答题卡交回。‎ 一、选择题（本大题8小题，每小题4分，共32分）在每小题列出的四个选项中，只有一个是正确的，请将答题卡上对应的小题所选的选项涂黑．‎ ‎1．的算术平方根是（ ）‎ A． B． C． D． ‎ ‎2．计算结果是（ ）‎ A． B． C． D．‎ ‎3．如图所示几何体的主（正）视图是（ ）‎ A． B． 　　　　 C． D． ‎ ‎4．《广东省2009年重点建设项目计划（草案）》显示，港珠澳大桥工程估算总投资726亿元，用科学记数法表示正确的是（ ）‎ A． 元 B．元 C．元 D．元 ‎ ‎5.满足2（x-1）≤x+2的正整数x有多少个（ ）‎ A．3 B‎.4 C.5 D.6‎ ‎6.数据3,3,4,5,4,3,6的众数和中位数分别是( )‎ A.3,3 B.4,‎4 C.4，3 D.3，4‎ ‎7.已知菱形ABCD的边长为8,∠A=120°，则对角线BD长是多少（ ）‎ A．12 B‎.12‎ C.8 D.8‎ ‎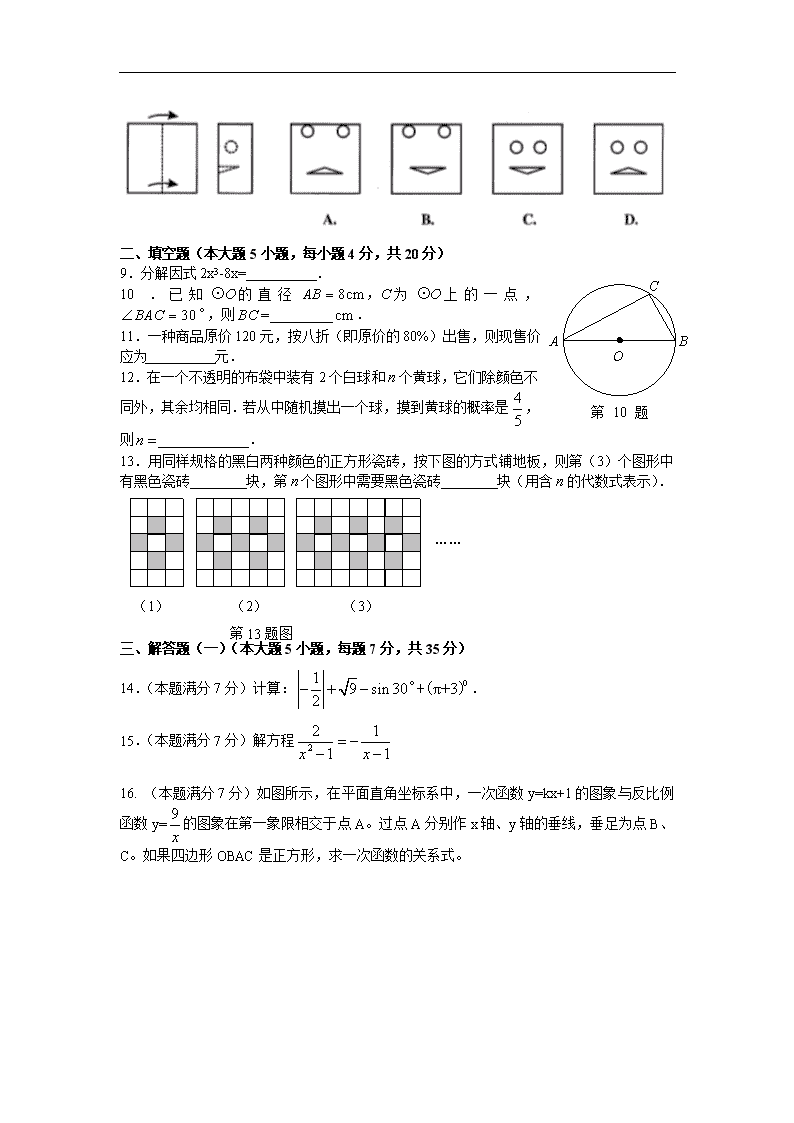8.如图所示的矩形纸片，先沿虚线按箭头方向向右对折，接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形，然后将纸片打开是下列图中的哪一个 二、填空题（本大题5小题，每小题4分，共20分）‎ ‎9．分解因式2x3-8x= ．‎ 第10题图 A C B O ‎10．已知的直径为上的一点，，则= ．‎ ‎11．一种商品原价120元，按八折（即原价的80%）出售，则现售价应为 元．‎ ‎12．在一个不透明的布袋中装有2个白球和个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，摸到黄球的概率是，则_____________．‎ ‎13．用同样规格的黑白两种颜色的正方形瓷砖，按下图的方式铺地板，则第（3）个图形中有黑色瓷砖 块，第个图形中需要黑色瓷砖________块（用含的代数式表示）．‎ 第13题图 ‎ ……‎ ‎（1） （2） （3）‎ 三、解答题（一）（本大题5小题，每题7分，共35分）‎ ‎14．（本题满分7分）计算：．‎ ‎15．（本题满分7分）解方程 ‎ ‎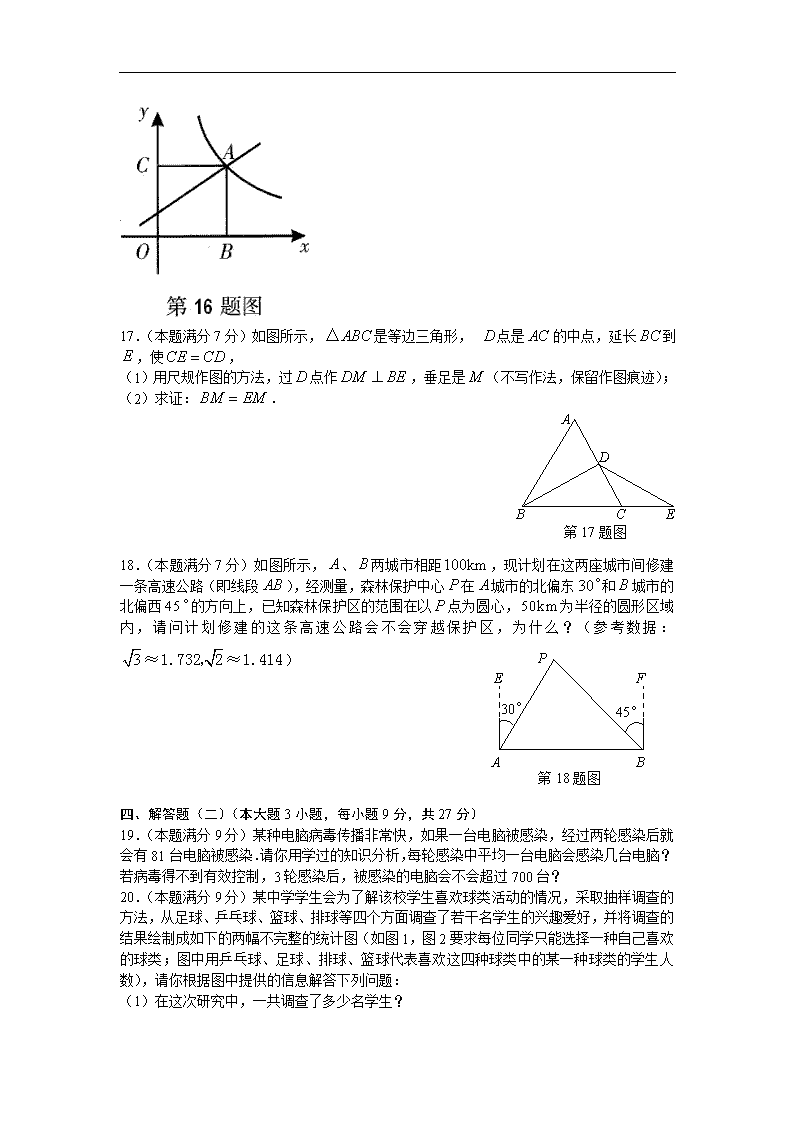16. （本题满分7分）如图所示，在平面直角坐标系中，一次函数y=kx+1的图象与反比例函数y=的图象在第一象限相交于点A。过点A分别作x轴、y轴的垂线，垂足为点B、C。如果四边形OBAC是正方形，求一次函数的关系式。‎ ‎17．（本题满分7分）如图所示，是等边三角形， 点是的中点，延长到，使，‎ ‎（1）用尺规作图的方法，过点作，垂足是（不写作法，保留作图痕迹）；‎ ‎（2）求证：．‎ A C B D E 第17题图 ‎30°‎ A B F E P ‎45°‎ 第18题图 ‎18．（本题满分7分）如图所示，、两城市相距，现计划在这两座城市间修建一条高速公路（即线段），经测量，森林保护中心在城市的北偏东和城市的北偏西的方向上，已知森林保护区的范围在以点为圆心，为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据：）‎ 四、解答题（二）（本大题3小题，每小题9分，共27分）‎ ‎19．（本题满分9分）某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染．请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？‎ ‎20．（本题满分9分）某中学学生会为了解该校学生喜欢球类活动的情况，采取抽样调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好，并将调查的结果绘制成如下的两幅不完整的统计图（如图1，图2要求每位同学只能选择一种自己喜欢的球类；图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数），请你根据图中提供的信息解答下列问题：‎ ‎（1）在这次研究中，一共调查了多少名学生？‎ ‎（2）喜欢排球的人数在扇形统计图中所占的圆心角是多少度？‎ ‎（3）补全频数分布折线统计图．‎ 图2‎ 人数 乒乓球 ‎20%‎ 足球 排球 篮球 ‎40%‎ ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ O 项目 足球 乒乓球 篮球 排球 图1‎ 第20题图 ‎21．（本题满分9分）如图所示，在矩形中，，两条对角线相交于点．以、为邻边作第1个平行四边形，对角线相交于点，再以、为邻边作第2个平行四边形，对角线相交于点；再以、为邻边作第3个平行四边形……依次类推．‎ ‎（1）求矩形的面积；‎ A1‎ O1‎ A2‎ B2‎ B1‎ C1‎ B C2‎ A O D 第21题图 C ‎（2）求第1个平行四边形、第2个平行四边形和第6个平行四边形的面积．‎ 五、解答题（三）（本大题3小题，每小题12分，共36分）‎ ‎22、（本题满分12分）‎ 第22题图 A E O G F B C D A E O B C D 图1‎ 图2‎ ‎（1）如图1，圆心接中，，、为的半径，于点，于点 求证：阴影部分四边形的面积是的面积的．‎ ‎（2）如图2，若保持角度不变，‎ 求证：当绕着点旋转时，由两条半径和的两条边围成的图形（图中阴影部分）面积始终是的面积的．‎ ‎23．（本题满分12分）小明用下面的方法求出方程的解，请你仿照他的方法求出下面另外两个方程的解，并把你的解答过程填写在下面的表格中．‎ 方程 换元法得新方程 解新方程 检验 求原方程的解 令 则 所以 N D A CD B M 第24题图 ‎24．（本题满分12分）正方形边长为4，、分别是、上的两个动点，当点在上运动时，保持和垂直，‎ ‎（1）证明：；‎ ‎（2）设，梯形的面积为，求与之间的函数关系式；当点运动到什么位置时，四边形面积最大，并求出最大面积；‎ ‎（3）当点运动到什么位置时，求的值．‎ ‎2009年广东省汕头市初中毕业生学业考试 数学试题参考答案及评分建议 一、选择题（本大题8小题，每小题4分，共32分）‎ ‎1．B 2．A 3．B 4．A 5.C 6.D 7.D 8．C 二、填空题（本大题5小题，每小题4分，共20分）‎ ‎9．2x（x+2）（x-2） 10．4 11．96 12．8 13．10，‎ 三、解答题（一）（本大题5小题，每题7分，共35分）‎ ‎14．解：原式= 4分 ‎=4． 7分 ‎15．解：方程两边同时乘以， 2分 ‎， 4分 ‎， 5分 经检验：是方程的解． 7分 ‎16.依题意可得：xy=9=OB·OC，……………………2分 又四边形ABCD为正方形，所以 OC=OB=3‎ 所以有 A（3，3）， ……………………3分 直线y＝kx＋1过点A，所以得3＝3k＋1，‎ 所以 k＝ ……………………5分 故有直线 y＝ x＋1 ……………………7分 ‎17．解：（1）作图见答案17题图，‎ 答案17题图 A C B D E M ‎ 2分 ‎（2）是等边三角形，是的中点，‎ 平分（三线合一），‎ ‎． 4分 ‎，‎ ‎．‎ 又，‎ ‎． 5分 又，‎ ‎，‎ ‎，‎ ‎．‎ 又，‎ ‎． 7分 答案18题图 A B F E P C ‎18．解：过点作，是垂足，‎ 则，， 2分 ‎，，‎ ‎， 4分 ‎，‎ ‎， 6分 ‎，‎ 答：森林保护区的中心与直线的距离大于保护区的半径，所以计划修筑的这条高速公路不会穿越保护区． 7分 四、解答题（二）（本大题3小题，每小题9分，共27分）‎ ‎19．解：设每轮感染中平均每一台电脑会感染台电脑， 1分 依题意得：， 4分 ‎，‎ 或，‎ ‎（舍去）， 6分 ‎． 8分 答：每轮感染中平均每一台电脑会感染8台电脑，3轮感染后，被感染的电脑会超过700台． 9分 ‎20．解：（1）（人）． 1分 ‎（2）， 2分 ‎，‎ ‎． 4分 ‎（3）喜欢篮球的人数：（人）， 5分 喜欢排球的人数：（人）． 7分 答案20题图 人数 ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ O 项目 足球 乒乓球 篮球 排球 ‎ 9分 ‎21．解：（1）在中，‎ ‎，‎ ‎． 2分 ‎（2）矩形，对角线相交于点，‎ ‎． 4分 四边形是平行四边形，‎ ‎，‎ ‎．‎ 又，‎ ‎，‎ ‎， 6分 同理，， 8分 第6个平行四边形的面积为． 9分 答案22题图（1）‎ A E O G F B C D 五、解答题（三）（本大题3小题，每小题12分，共36分）‎ ‎22．证明：（1）如图1，连结，‎ 因为点是等边三角形的外心，‎ 所以． 2分 ‎，‎ 因为，‎ 所以． 5分 ‎（2）解法一：‎ 答案22题图（2）‎ A E O G F B C D ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 连结和，则，， 6分 不妨设交于点，交于点，‎ ‎，‎ ‎． 8分 在和中，‎ ‎， 10分 答案第22题图（3）‎ A E O G F B C D ‎1‎ ‎3‎ ‎2‎ H K ‎． 12分 解法二：‎ 不妨设交于点，交于点，‎ 作，垂足分别为， 6分 在四边形中，，‎ ‎， 8分 即．‎ 又，‎ ‎． 8分 ‎，‎ ‎，‎ ‎， 10分 ‎． 12分 ‎23．解：‎ 方程 换元法得新方程 解新方程 检验 求原方程的解 令，则 ‎……1分 ‎……2分 ‎（舍去）‎ ‎……3分 ‎，所以．‎ ‎……4分 令，则 ‎……6分 ‎……8分 ‎（舍去）‎ ‎……10分 ‎，所以．‎ ‎……12分 ‎24．解：（1）在正方形中，，‎ N D A CD B M 答案24题图 ‎，‎ ‎，‎ ‎．‎ 在中，，‎ ‎，‎ ‎． 3分 ‎（2），‎ ‎，‎ ‎， 5分 ‎，‎ 当时，取最大值，最大值为10． 7分 ‎（3），‎ 要使，必须有， 9分 由（1）知，‎ ‎，‎ 当点运动到的中点时，，此时． 12分 ‎（其它正确的解法，参照评分建议按步给分）‎