2018年浙江省衢州市中考数学试卷含答案 18页

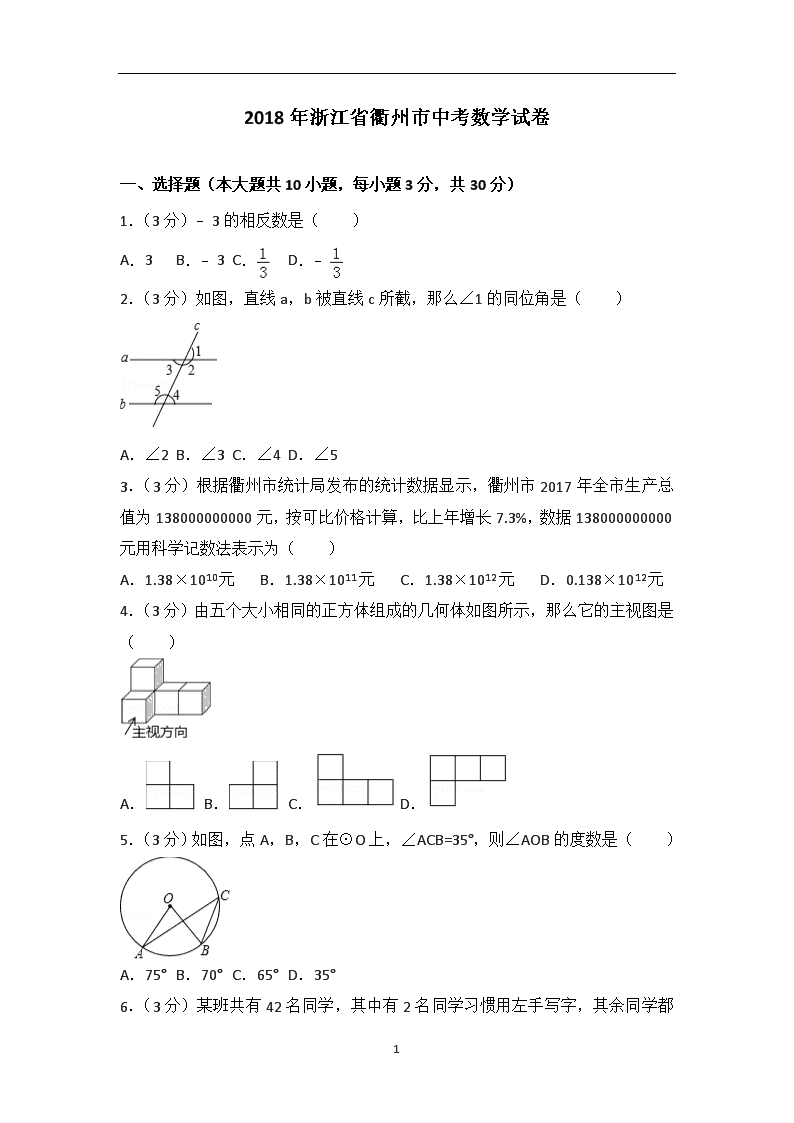
‎2018年浙江省衢州市中考数学试卷 ‎　‎ 一、选择题（本大题共10小题，每小题3分，共30分）‎ ‎1．（3分）﹣3的相反数是（　　）‎ A．3 B．﹣3 C． D．﹣‎ ‎2．（3分）如图，直线a，b被直线c所截，那么∠1的同位角是（　　）‎ A．∠2 B．∠3 C．∠4 D．∠5‎ ‎3．（3分）根据衢州市统计局发布的统计数据显示，衢州市2017年全市生产总值为138000000000元，按可比价格计算，比上年增长7.3%，数据138000000000元用科学记数法表示为（　　）‎ A．1.38×1010元 B．1.38×1011元 C．1.38×1012元 D．0.138×1012元 ‎4．（3分）由五个大小相同的正方体组成的几何体如图所示，那么它的主视图是（　　）‎ A． B． C． D．‎ ‎5．（3分）如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（　　）‎ A．75° B．70° C．65° D．35°‎ 18‎ ‎6．（3分）某班共有42名同学，其中有2名同学习惯用左手写字，其余同学都习惯用右手写字，老师随机请1名同学解答问题，习惯用左手写字的同学被选中的概率是（　　）‎ A．0 B． C． D．1‎ ‎7．（3分）不等式3x+2≥5的解集是（　　）‎ A．x≥1 B．x≥ C．x≤1 D．x≤﹣1‎ ‎8．（3分）如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE=32°，则∠GHC等于（　　）‎ A．112° B．110° C．108° D．106°‎ ‎9．（3分）如图，AB是圆锥的母线，BC为底面半径，已知BC=6cm，圆锥的侧面积为15πcm2，则sin∠ABC的值为（　　）‎ A． B． C． D．‎ ‎10．（3分）如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（　　）‎ A．3cm B．cm C．2.5cm D．cm ‎　‎ 二、填空题（本大题共6小题，每小题4分，共24分）‎ 18‎ ‎11．（4分）分解因式：x2﹣9=　 　．‎ ‎12．（4分）数据5，5，4，2，3，7，6的中位数是　 　．‎ ‎13．（4分）如图，在△ABC和△DEF中，点B，F，C，E在同一直线上，BF=CE，AB∥DE，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是　 　（只需写一个，不添加辅助线）．‎ ‎14．（4分）星期天，小明上午8：00从家里出发，骑车到图书馆去借书，再骑车回到家．他离家的距离y（千米）与时间t（分钟）的关系如图所示，则上午8：45小明离家的距离是　 　千米．‎ ‎15．（4分）如图，点A，B是反比例函数y=（x＞0）图象上的两点，过点A，B分别作AC⊥x轴于点C，BD⊥x轴于点D，连接OA，BC，已知点C（2，0），BD=2，S△BCD=3，则S△AOC=　 　．‎ ‎16．（4分）定义：在平面直角坐标系中，一个图形先向右平移a个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫作图形的γ（a，θ）变换．‎ 如图，等边△ABC的边长为1，点A在第一象限，点B与原点O重合，点C在x轴的正半轴上．△A1B1C1就是△ABC经γ（1，180°）变换后所得的图形．‎ 18‎ 若△ABC经γ（1，180°）变换后得△A1B1C1，△A1B1C1经γ（2，180°）变换后得△A2B2C2，△A2B2C2经γ（3，180°）变换后得△A3B3C3，依此类推……‎ ‎△An﹣1Bn﹣1Cn﹣1经γ（n，180°）变换后得△AnBnCn，则点A1的坐标是　 　，点A2018的坐标是　 　．‎ ‎　‎ 三、解答题（本大题共8小题，第17-19小题每小题6分，第20-21小题每小题6分，第22-23小题每小题6分，第24小题12分，共66分）‎ ‎17．（6分）计算：|﹣2|﹣+23﹣（1﹣π）0．‎ ‎18．（6分）如图，在▱ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F，求证：AE=CF．‎ ‎19．（6分）有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：‎ 小明发现这三种方案都能验证公式：a2+2ab+b2=（a+b）2，‎ 对于方案一，小明是这样验证的：‎ a2+ab+ab+b2=a2+2ab+b2=（a+b）2‎ 18‎ 请你根据方案二、方案三，写出公式的验证过程．‎ 方案二：‎ 方案三：‎ ‎20．（8分）“五•一”期间，小明到小陈家所在的美丽乡村游玩，在村头A处小明接到小陈发来的定位，发现小陈家C在自己的北偏东45°方向，于是沿河边笔直的绿道l步行200米到达B处，这时定位显示小陈家C在自己的北偏东30°方向，如图所示，根据以上信息和下面的对话，请你帮小明算一算他还需沿绿道继续直走多少米才能到达桥头D处（精确到1米）（备用数据：≈1.414，≈1.732）‎ ‎21．（8分）为响应“学雷锋、树新风、做文明中学生”号召，某校开展了志愿者服务活动，活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项，活动期间，随机抽取了部分学生对志愿者服务情况进行调查，结果发现，被调查的每名学生都参与了活动，最少的参与了1项，最多的参与了5项，根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图．‎ ‎（1）被随机抽取的学生共有多少名？‎ 18‎ ‎（2）在扇形统计图中，求活动数为3项的学生所对应的扇形圆心角的度数，并补全折线统计图；‎ ‎（3）该校共有学生2000人，估计其中参与了4项或5项活动的学生共有多少人？‎ ‎22．（10分）如图，已知AB为⊙O直径，AC是⊙O的切线，连接BC交⊙O于点F，取的中点D，连接AD交BC于点E，过点E作EH⊥AB于H．‎ ‎（1）求证：△HBE∽△ABC；‎ ‎（2）若CF=4，BF=5，求AC和EH的长．‎ ‎23．（10分）某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．‎ ‎（1）求水柱所在抛物线（第一象限部分）的函数表达式；‎ ‎（2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？‎ ‎（3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．‎ ‎24．（12分）如图，Rt△‎ 18‎ OAB的直角边OA在x轴上，顶点B的坐标为（6，8），直线CD交AB于点D（6，3），交x轴于点C（12，0）．‎ ‎（1）求直线CD的函数表达式；‎ ‎（2）动点P在x轴上从点（﹣10，0）出发，以每秒1个单位的速度向x轴正方向运动，过点P作直线l垂直于x轴，设运动时间为t．‎ ‎①点P在运动过程中，是否存在某个位置，使得∠PDA=∠B？若存在，请求出点P的坐标；若不存在，请说明理由；‎ ‎②请探索当t为何值时，在直线l上存在点M，在直线CD上存在点Q，使得以OB为一边，O，B，M，Q为顶点的四边形为菱形，并求出此时t的值．‎ ‎　‎ 18‎ ‎2018年浙江省衢州市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共10小题，每小题3分，共30分）‎ ‎1．‎ ‎【解答】解：﹣3的相反数是3，‎ 故选：A．‎ ‎　‎ ‎2．‎ ‎【解答】解：由同位角的定义可知，‎ ‎∠1的同位角是∠4，‎ 故选：C．‎ ‎　‎ ‎3．‎ ‎【解答】解：将138000000000用科学记数法表示为：1.38×1011．‎ 故选：B．‎ ‎　‎ ‎4．‎ ‎【解答】解：从正面看得到3列正方形的个数依次为2，1，1，‎ 故选：C．‎ ‎　‎ ‎5．‎ ‎【解答】解：∵∠ACB=35°，‎ ‎∴∠AOB=2∠ACB=70°．‎ 故选：B．‎ ‎　‎ ‎6．‎ ‎【解答】解：∵‎ 18‎ 某班共有42名同学，其中有2名同学习惯用左手写字，其余同学都习惯用右手写字，‎ ‎∴老师随机请1名同学解答问题，习惯用左手写字的同学被选中的概率是：=．‎ 故选：B．‎ ‎　‎ ‎7．‎ ‎【解答】解：3x≥3‎ x≥1‎ 故选：A．‎ ‎　‎ ‎8．‎ ‎【解答】解：∵∠AGE=32°，‎ ‎∴∠DGE=148°，‎ 由折叠可得，∠DGH=∠DGE=74°，‎ ‎∵AD∥BC，‎ ‎∴∠GHC=180°﹣∠DGH=106°，‎ 故选：D．‎ ‎　‎ ‎9．‎ ‎【解答】解：设圆锥的母线长为R，由题意得 ‎15π=π×3×R，‎ 解得R=5．‎ ‎∴圆锥的高为4，‎ ‎∴sin∠ABC==，‎ 故选：C．‎ ‎　‎ ‎10．‎ 18‎ ‎【解答】解：连接OB，‎ ‎∵AC是⊙O的直径，弦BD⊥AO于E，BD=8cm，AE=2cm，‎ 在Rt△OEB中，OE2+BE2=OB2，‎ 即OE2+42=（OE+2）2‎ 解得：OE=3，‎ ‎∴OB=3+2=5，‎ ‎∴EC=5+3=8，‎ 在Rt△EBC中，BC=，‎ ‎∵OF⊥BC，‎ ‎∴∠OFC=∠CEB=90°，‎ ‎∵∠C=∠C，‎ ‎∴△OFC∽△BEC，‎ ‎∴，‎ 即，‎ 解得：OF=，‎ 故选：D．‎ ‎　‎ 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎11．‎ ‎【解答】解：x2﹣9=（x+3）（x﹣3）．‎ 故答案为：（x+3）（x﹣3）．‎ ‎　‎ ‎12．‎ 18‎ ‎【解答】解：从小到大排列此数据为：2、3、4、5、5、6、7，‎ 一共7个数据，其中5处在第4位为中位数．‎ 故答案为：5．‎ ‎　‎ ‎13．‎ ‎【解答】解：添加AB=ED，‎ ‎∵BF=CE，‎ ‎∴BF+FC=CE+FC，‎ 即BC=EF，‎ ‎∵AB∥DE，‎ ‎∴∠B=∠E，‎ 在△ABC和△DEF中，‎ ‎∴△ABC≌△DEF（SAS），‎ 故答案为：AB=ED．‎ ‎　‎ ‎14．‎ ‎【解答】解：设当40≤t≤60时，距离y（千米）与时间t（分钟）的函数关系为y=kt+b，‎ ‎∵图象经过（40，2）（60，0），‎ ‎∴，‎ 解得：，‎ ‎∴y与t的函数关系式为y=﹣x+6，‎ 当t=45时，y=﹣×45+6=1.5，‎ 故答案为：1.5．‎ ‎　‎ ‎15．‎ 18‎ ‎【解答】解：∵BD⊥CD，BD=2，‎ ‎∴S△BCD=BD•CD=3，即CD=3，‎ ‎∵C（2，0），即OC=2，‎ ‎∴OD=OC+CD=2+3=5，‎ ‎∴B（5，2），‎ 代入反比例解析式得：k=10，即y=，‎ 则S△AOC=5，‎ 故答案为：5‎ ‎　‎ ‎16．‎ ‎【解答】解：根据图形的γ（a，θ）变换的定义可知：‎ 对图形γ（n，180°）变换，就是先进行向右平移n个单位变换，再进行关于原点作中心对称变换．‎ ‎△ABC经γ（1，180°）变换后得△A1B1C1，A1 坐标（﹣，﹣）‎ ‎△A1B1C1经γ（2，180°）变换后得△A2B2C2，A2坐标（﹣，）‎ ‎△A2B2C2经γ（3，180°）变换后得△A3B3C3，A3坐标（﹣，﹣）‎ ‎△A3B3C3经γ（3，180°）变换后得△A4B4C4，A4坐标（﹣，）‎ 依此类推……‎ 可以发现规律：An横坐标存在周期性，每3次变换为一个周期，纵坐标为 当n=2018时，有2018÷3=672余2‎ 所以，A2018横坐标是﹣，纵坐标为 故答案为：（﹣，﹣），（﹣，）．‎ ‎　‎ 三、解答题（本大题共8小题，第17-19小题每小题6分，第20-21小题每小题6分，第22-23小题每小题6分，第24小题12分，共66分）‎ 18‎ ‎17．‎ ‎【解答】解：原式=2﹣3+8﹣1=6．‎ ‎　‎ ‎18．‎ ‎【解答】证明：如图，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AB=CD，AB∥CD，‎ ‎∴∠BAE=∠DCF．‎ 又BE⊥AC，DF⊥AC，‎ ‎∴∠AEB=∠CFD=90°．‎ 在△ABE与△CDF中，‎ ‎，‎ ‎∴得△ABE≌△CDF（AAS），‎ ‎∴AE=CF．‎ ‎　‎ ‎19．‎ ‎【解答】解：由题意可得，‎ 方案二：a2+ab+（a+b）b=a2+ab+ab+b2=a2+2ab+b2=（a+b）2，‎ 方案三：a2+==a2+2ab+b2=（a+b）2．‎ ‎　‎ ‎20．‎ ‎【解答】解：如图所示：可得：∠CAD=45°，∠CBD=60°，AB=200m，‎ 则设BD=x，故DC=x，‎ 18‎ ‎∵AD=DC，‎ ‎∴200+x=x，‎ 解得：x=100（+1）≈273，‎ 答：小明还需沿绿道继续直走273米才能到达桥头D处．‎ ‎　‎ ‎21．‎ ‎【解答】解：（1）被随机抽取的学生共有14÷28%=50（人）；‎ ‎（2）活动数为3项的学生所对应的扇形圆心角=×360°=72°，‎ 活动数为5项的学生为：50﹣8﹣14﹣10﹣12=6，‎ 如图所示：‎ ‎（3）参与了4项或5项活动的学生共有×2000=720（人）．‎ ‎　‎ ‎22．‎ ‎【解答】解：（1）∵AC是⊙O的切线，‎ ‎∴CA⊥AB，∵EH⊥AB，‎ ‎∴∠EHB=∠CAB，∵∠EBH=∠CBA，‎ ‎∴△HBE∽△ABC．‎ ‎（2）连接AF．‎ 18‎ ‎∵AB是直径，‎ ‎∴∠AFB=90°，‎ ‎∵∠C=∠C，∠CAB=∠AFC，‎ ‎∴△CAF∽△CBA，‎ ‎∴CA2=CF•CB=36，‎ ‎∴CA=6，AB==3，AF==2，‎ ‎∵=，‎ ‎∴∠EAF=∠EAH，∵EF⊥AF，EH⊥AB，‎ ‎∴EF=EH，∵AE=AE，‎ ‎∴Rt△AEF≌Rt△AEH，‎ ‎∴AF=AH=2，设EF=EH=x，‎ 在Rt△EHB中，（5﹣x）2=x2+（）2，‎ ‎∴x=2，‎ ‎∴EH=2．‎ ‎　‎ ‎23．‎ ‎【解答】解：（1）设水柱所在抛物线（第一象限部分）的函数表达式为y=a（x﹣3）2+5（a≠0），‎ 将（8，0）代入y=a（x﹣3）2+5，得：25a+5=0，‎ 解得：a=﹣，‎ ‎∴水柱所在抛物线（第一象限部分）的函数表达式为y=﹣（x﹣3）2+5（0＜x＜8）．‎ 18‎ ‎（2）当y=1.8时，有﹣（x﹣3）2+5=1.8，‎ 解得：x1=﹣1，x2=7，‎ ‎∴为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心7米以内．‎ ‎（3）当x=0时，y=﹣（x﹣3）2+5=．‎ 设改造后水柱所在抛物线（第一象限部分）的函数表达式为y=﹣x2+bx+，‎ ‎∵该函数图象过点（16，0），‎ ‎∴0=﹣×162+16b+，解得：b=3，‎ ‎∴改造后水柱所在抛物线（第一象限部分）的函数表达式为y=﹣x2+3x+=﹣（x﹣）2+．‎ ‎∴扩建改造后喷水池水柱的最大高度为米．‎ ‎　‎ ‎24．‎ ‎【解答】解：（1）设直线CD的解析式为y=kx+b，则有，‎ 解得，‎ ‎∴直线CD的解析式为y=﹣x+6．‎ ‎（2）①如图1中，作DP∥OB，则∠PDA=∠B．‎ ‎∵DP∥OB，‎ ‎∴=，‎ ‎∴=，‎ 18‎ ‎∴PA=，‎ ‎∴OP=6﹣=，‎ ‎∴P（，0），根据对称性可知，当AP=AP′时，P′（，0），‎ ‎∴满足条件的点P坐标为（，0）或（，0）．‎ ‎②如图2中，当OP=OB=10时，作PQ∥OB交CD于Q．‎ ‎∵直线OB的解析式为y=x，‎ ‎∴直线PQ的解析式为y=x+，‎ 由，解得，‎ ‎∴Q（﹣4，8），‎ ‎∴PQ==10，‎ ‎∴PQ=OB，∵PQ∥OB，‎ ‎∴四边形OBQP是平行四边形，‎ ‎∵OB=OP，‎ ‎∴四边形OBQP是菱形，此时点M与的Q重合，满足条件，t=0．‎ 如图3中，当OQ=OB时，设Q（m，﹣m+6），‎ 18‎ 则有m2+（﹣m+6）2=102，‎ 解得m=，‎ ‎∴点Q 的横坐标为或，设点M的横坐标为a，‎ 则有：=或=，‎ ‎∴a=或，‎ ‎∴满足条件的t的值为或．‎ 如图4中，当点Q与C重合时，M点的横坐标为6，此时t=16，‎ 综上所述，满足条件的t的值为0或16或或．‎ ‎　‎ 18‎