人教版九年级上册数学期末考试经典复习题五 15页

C O A B P 初三上学期数学期末考试经典复习题五 考生 须知 1. 本试卷为闭卷考试，满分为 120 分，考试时间为 120 分钟． 2. 本试卷共 8 页，各题答案均答在本题规定的位置． 题号 一 二 三 四 五 六 七 八 九 总分 分数 一、选择题（本题共 8 个小题，每小题 4 分，共 32 分） 在每个小题给出的四个备选答案中，只有一个是符合题目要求的，请把所选答案的字母填在题后的括 号内 . 1 ．若 : 2:3x y  ，则下列各式中正确的式子是（） A．3 2x y B . 2 3x y C . 3 2 x y D . 1 3 x y y   2 ．在 △ ABC 中， ∠ C =90° ， 3sin 5A  ，那么cos B 的值等于（） A． 3 5 B . 4 5 C . 3 4 D . 4 3 3 ．如图，反比例函数的图象过点 M，则此反比例函数的解析式为（） A． 2y x  B . 2y x   C . 1 2y x  D . 1 2y x   4. 如图，等边△ABC 内接与 ⊙ O，动点 P 在圆周的劣弧 AB 上， 且不与 A、B 重合，则∠BPC 等于 ( )A .30° B . 60° C . 90° D . 45° 5 ．已知函数 2y ax ax  与函数 ( 0)ay ax   ，则它们在同一坐标系中的大致图象是（） 第 3 题图 第 4 题图 M F E D B A C 第 13 题图 ABCD 6 ．已知⊙ 1O 的半径为 2 cm，⊙ 2O 的半径为 4 cm，圆心距 1O 2O 为 3 cm，则⊙ 1O 与⊙ 2O 的位置关系 是（） A . 外离 B . 外切 C . 相交 D . 内切 7．把二次函数 22y x 的图象向右平移 2 个单位，再向上平移 3 个单位后，得到的图象的函数解析式为() A. 22( 2) 3y x   B. 22( 2) 3y x   C. 22( 2) 3y x   D. 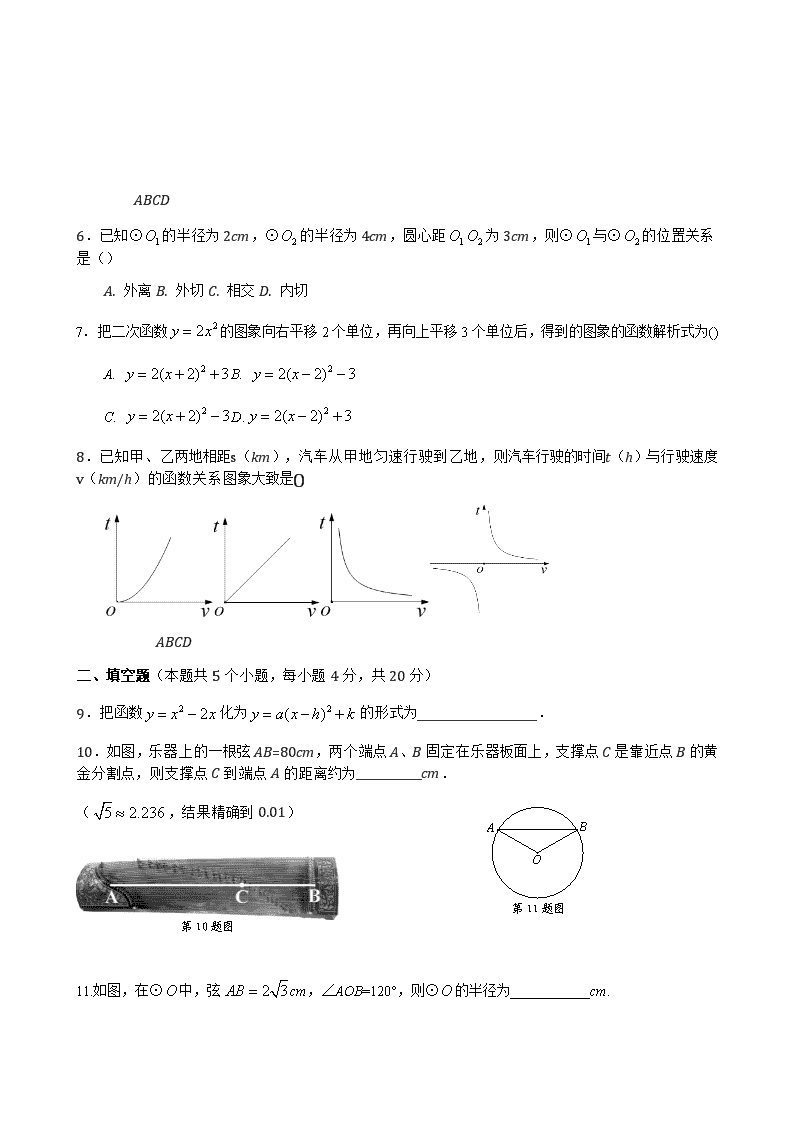22( 2) 3y x   8 ．已知甲、乙两地相距 s （km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t（h）与行驶速度 v （km / h）的函数关系图象大致是 () ABCD 二、填空题（本题共 5 个小题，每小题 4 分，共 20 分） 9 ．把函数 2 2y x x  化为 2( )y a x h k   的形式为 ______________________ ． 10 ．如图，乐器上的一根弦 AB =80 cm，两个端点 A、B 固定在乐器板面上，支撑点 C 是靠近点 B 的黄 金分割点，则支撑点 C 到端点 A 的距离约为 ____________ cm． （ 5 2.236 ，结果精确到 0.01 ） 11.如图，在⊙O 中，弦 2 3AB  cm，∠AOB=120°，则⊙O 的半径为__________cm. 12.若两个相似多边形的周长分别为 40cm 和 70cm，面积的和为 65cm2，则较小 A O B 第 11 题图 第 10 题图 A E B C D 多边形的面积为____________cm2. 13. 如图，  ABCD 中，BC =6 ，BC 边上高为 4 ，M 为 BC 中点，若分别以 B、C 为圆心，BM 长为半径 画弧，交 AB、CD 于 E、F 两点，则图中阴影部分面积是 ________. 三、解答题（本题共 5 个小题，每小题 5 分，共 25 分） 14 ．计算： 4cos60 tan 45 2sin 60    ． 解： 15 ．二次函数的图象经过点（ 1 ， 2 ）和（ 0 ， -1 ）且对称轴为 x =2 ，求二次函数解析式． 解： 16 ．如图，在 △ ABC 中，DE ∥ BC，AD =4 ，DB =3 ，AC =10 ，求 AE 的长． 解： P O B A 第 17 题图 17 ．如图，PA、PB 是 ⊙ O 的切线，切点分别是 A、B，若 ∠ APB =60° ，PA =4 ． 求 ⊙ O 的半径． 18 ．把三张完全相同的长方形卡片分别标上数字 1 、 2 、 3 ，洗匀后将标有数字的一面朝下，放在桌面 上 .（ 1 ）如果从中随机抽取一张卡片，求卡片上的数字为 2 的概率 .（ 2 ）如果先从卡片中随机抽取一张，记下卡片上的数字后放回，洗匀后将标有数字的一面朝下，再 从中随即抽取一张，记下第二张卡片上的数字，请你画出树状图并求出前后两张卡片上所标的数字不 相同的概率 .解： 第 19 题图 A C O E B 第 20 题图 A C B D 四、解答题（本题共 2 个小题，每小题 5 分，共 10 分） 19 ．如图，AB 是 ⊙ O 的弦，OC⊥OA 交 AB 于点 C，过 B 的直线交 OC 的延长线于点 E，当 CE = BE 时， 直线 BE 与 ⊙ O 有怎样的位置？请说明理由 . 20 ．已知：如图，在 △ ABC 中， ∠ C =90° ， ∠ B =30° ，AD 是 ∠ BAC 的平分线，且 AB = 4 3 ，求：AD 的长 及 ADBS ． 解： 第 22 题图 五、解答题（本题 6 分） 21 ．在平面直角坐标系 xoy 中， 二次函数 1C ： 2y ax bx c   的图象与 2C ： 22 4 3y x x   的图象关于 y 轴对称，且 1C 与直线 2y mx  交与点 A（n， 1 ） . 试确定 m 的值 .解： 六、解答题（本题 6 分） 22 ．如图，河对岸有铁塔 AB，在 C 处测得塔顶 A 的仰角为 30° ，向塔前进 14 米到达 D 处，在 D 处测 得 A 的仰角为 45° ，求铁塔 AB 的高（结果可以带根号） .解： 七、解答题（本题 6 分） 23 ．某商场以每件 30 元的价格购进一种商品，试销中发现，这种商品每天的销售量 m（件）与每件 销售价 x（元）满足一次函数 m =162-3 x (30< x <54).（ 1 ）写出商场卖这种商品每天的销售利润 y ( 元 ) 与每件的售价 x ( 元 ) 之间的函数解析式 .（ 2 ）如果商场要想每天获得最大的销售利润，每件商品的售价定为多少元合适？ 最大利润是多少元？ 解： G F E D C O B A 第 24 题图 八、解答题（本题共 7 分） 24 ．如图，等腰 △ ABC 中，AB = AC =13 ，BC =10 ，以 AC 为直径作 ⊙ O 交 BC 于点 D，交 AB 于点 G，过 点 D 作 ⊙ O 的切线交 AB 于点 E，交 AC 的延长线与点 F .（ 1 ）求证：EF⊥AB； （ 2 ）求 co s∠ F 的值 .解： 九、解答题（本题 8 分） 25 ．在平面直角坐标系 xoy 中，已知关于 x 的二次函数 2 ( 1) 2 1y x k x k     的图象与 x 轴交于 A、 B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C（ 0 ， -3 ） .（ 1 ）求这个二次函数的解析式及 A、B 两点的坐标； （ 2 ）若直线 l： ( 0)y kx k  与线段 BC 交于点 D（点 D 与 B、C 不重合），则是否存在这样的直线 l， 使得以 B、O、D 为顶点的三角形与 △ ABC 相似？若存在，求出该直线的函数解析式及点 D 的坐标；若 不存在，求说明理由 .解： 参考答案 阅卷须知： 1．一律用红钢笔或红圆珠笔批阅． 2．为了阅卷方便，解答题中的推倒步骤写得较为详细，考生只要写明主要过程即可．若考生的解法 与本解法不同，正确者可参照平分参考给分，解答右端所注分数，表示考生正确做到这一步应得的累 加分数． 一、选择题（共 8 个小题，每小题 4 分，共 32 分） 题 号 1 2 3 4 5 6 7 8答 案 A A B B B C D C 二、填空题（共 5 个小题，每小题 4 分，共 20 分） 9 ． 2( 1) 1y x   ； 10 ． 49.44 ； 11 ． 2 ； 12 ． 16 ； 13 ． 924 2  三、解答题（共 5 个小题，每小题 5 分，共 25 分） 14. 解： 4cos60 tan 45 2sin 60    A E B C D 第 16 题图 = 14 12 32 2    …………………………………………………………………………… 3 分 = 1 3 …………………………………………………………………………… 4 分 = 3 3 ………………………………………………………………………………… 5 分 15. 解：设二次函数的解析式为 2y ax bx c   ∵二次函数的图象对称轴为 x=2 且图象过点（1，2），（0，-1） ∴ 2 1 22 a b c c b a             …………………………………………………………………… 3 分 解得 1 4 1 a b c        ……………………………………………………………………… 4 分 ∴二次函数的解析式为： 2 4 1y x x    ……………………………………… 5 分 16. 解：∵DE∥BC ∴ AD AE AB AC  ……………………………………… 2 分 设 AE = x ∴ 4 3 4 10 x ……………………………………… 4 分 解得： 40 7x  …………………………………… 5 分 答：AE 的长为 40 7 17. 解：联结 OA、OP…………………………………… 1 分 ∵PA、PB 是 ⊙ O 的切线 ∴∠OAP=90°，∠APO= 1 2 ∠APB=30°……………… 3 分 P O B A 第 17 题图 R t △OAP 中，∵ t an∠APO = OA PA …………………… 4 分 ∴OA = PA t an 30 △ = 3 44 33 3   ………………… 5 分 18. （ 1 ）P（抽到数字是 2 的卡片） = 1 3 ……………………………………………… 2 分 （ 2 ）如图： ………………………… 4 分 ∵所有可能出现的结果共 9 种，其中前后不同的有 6 种 ∴P（前后两张卡片数字不相同）= 6 2 9 3  ……………………………………… 5 分 四、解答题（本题共 2 个小题，每小题 5 分，共 10 分） 19. 答：直线 BE 与 ⊙ O 相切 证明：联结 OB ∵OB = OA∴∠ 1= ∠A……………………………… 1 分 ∴CE = BE ∴∠ 2= ∠ 3 …………………………………………… 2 分 ∵∠ 3= ∠ 4∴∠ 2= ∠ 4 …………………………………………… 3 分 ∵OA⊥OC∴∠A + ∠ 4=90 ° ∴∠ 1+ ∠ 2=90 °……………………………………… 4 分 ∴OB⊥BE ∴直线 BE 与 ⊙ O 相切……………………………… 5 分 20. 解： ∵∠C =90 °，∠B =30 ° ∴∠BAC =60 °…………………………………… 1 分 3 2 1 3 2 1 1 2 3 2 3 1 3 第 19 题图 A C O E B1 2 4 第 20 题图 A C B D 12 ∵AB = 4 3 ∴AC = 1 2 AB= 1 2  4 3 = 2 3 …………………… 2 分 ∵AD 平分∠BAC ∴∠ 1= ∠ 2=30 °，∴∠ 1= ∠B 在 R t △ACD 中，c os ∠ 2= AC AD ∴AD = 2 3 4cos 2 3 2 AC   …………………………………… 3 分 ∵∠ 1= ∠B ∴BD = AD =4∴ 1 1 4 2 3 4 32 2ABDS BD AC      ………………… 4 分 ∴AD 的长为 4 ，△ABD 的面积为 4 3 . …………………… 5 分 五、解答题（本题 6 分） 21. 解： ∵二次函数 1C ： 2y ax bx c   的图象与 2C ： 22 4 3y x x   的图象关于 y 轴对称 ∴由对称性可知， 1C ： 22 4 3y x x   ………………………………………… 2 分 ∵ 1C 与直线 2y mx  交与点 A（n， 1 ） ∴ 22 4 3 1n n   得 1 2 1n n   ……………………………………………………………………… 4 分 ∴A（- 1 ， 1 ） ∵A（- 1 ， 1 ）在直线 2y mx  上 ∴ 1= - 1  m +2 ………………………………………………………………………… 5 分 第 21 题图 ∴m =1 ……………………………………………………………………………… 6 分 六、解答题（本题 6 分） 22. 解 ∵在 R t △ADB 中，∠ADB =45 ° ∴AB = DB 设 AB = x，则 DB = AB = x ∵CD =14 ∴CB =14+ x 在 R t △ACB 中， t an∠ACB = AB CB ∵∠ACD =30 ° ∴ t an 30 °B = 14 x x  ∴ 3 3 = 14 x x  解得 x =7 3 +7 经检验，x =7 3 +7 是所列方程的解 ∴铁塔 AB 的高为（ 7 3 +7) 米． 七、解答题（本题 6 分） 23. 解： （ 1 ）由题意得， 2( 30) ( 30)(162 3 ) 3 252 4860y x m x x x x         …… 2 分 （ 2 ）∵a = - 3<0 ∴y 有最大值………………………………………………………… 3 分 ∴当 422 bx a    时………………………………………………………………… 4 分 24 4324 ac by a  最大值 …………………………………………………………… 5 分 ∴当每件商品的售价为 42 元时，y 有最大利润为 432 元………………………… 6 分 八、解答题（本题满分 7 分） 24. 证明： （ 1 ）联结 OD…………………………………………… 1 分 ∵OC = OD∴∠ODC = ∠OCD 又∵AB = AC∴∠OCD = ∠B ∴∠ODC = ∠B∴OD∥AB……………………… 2 分 ∵ED 是 ⊙ O 的切线，OD 是 ⊙ O 的半径 ∴OD⊥EF∴AB⊥EF……………………… 3 分 （ 2 ）联结 AD、CG ∵AD 是 ⊙ O 的直径 ∴∠ADC = ∠AGC =90 ° ∵AB⊥EF∴DE∥CG ∴∠F = ∠GCA…………………………………………… 4 分 ∵AB = AC ∴DC = 1 2 BC =5 R t △ADC 中， 2 2 12AD AC CD   …………………………………………… 5 分 ∵AD BC = AB CG ∴CG = 120 13 AD BC AB  ……………………………………………………………… 6 分 R t △CGA 中，c os ∠GCA = 120 169 GC AC  ∴c os ∠F = 120 169 ………………………………………………………………………… 7 分 九、解答题（本题满分 8 分） G F E D C O B A 第 24 题图 G F E D C O B A 25. 解：（ 1 ）∵二次函数的图象过点 C（ 0 ，- 3 ） ∴ 2 k- 1= - 3解得：k = - 1 ……………………………………………………………………………… 1 分 ∴此二次函数的解析式为： 2 2 3y x x   令 y =0 得 1 1x   ， 2 3x  ∵点 A 在点 B 的左侧 ∴A（- 1 ， 0 ），B（ 3 ， 0 ）…………………………………………………………… 3 分 （ 2 ）假设满足条件的直线 l 存在 过点 D 做 DE⊥x 轴于点 E ∵点 A 的坐标为（- 1 ， 0 ），点 B 的坐标为（ 3 ， 0 ），点 C 的坐标为（ 0 ，- 3 ） ∴AB =4 ，OB = OC =3 ，∠OBC =45 ° ∴BC = 3 2 要使以 B、O、D 为顶点的三角形与△ABC 相似，以为已有∠OBD = ∠ABC， 则只需 OB DB AB BC  ①，或 OB DB BC AB  ②成立即可 ①当 OB DB AB BC  时 有 BD= 9 2 4 OB BC AB  …………………………………… 4 分 在 R t △BDE 中， DE = BD si n 45 ° = 9 4 ，BE = BD c os45 ° = 9 4 ∴OE = OB-BE =3 - 9 4 = 3 4 ∵点 D 在 x 轴的下方， ∴点 D 的坐标为（ 3 4 ， 9 4  ）……………………………………………………… 5 分 将点 D 的坐标代入 ( 0)y kx k  中，求得 k = - 3∴满足条件的直线 l 的函数解析式为 3y x  …………………………………… 6 分 图① [或求出直线 AC 的函数解析式为 3 3y x   ，则与直线 AC 平行的直线 l 的函数解析式为 3y x  ， 此时△BOD∽△BAC，再求出直线 BC 的函数解析式为 3y x  ，联立 3 3 y x y x      ，求得点 D 的坐标为 （ 3 4 ， 9 4  ），酌情给分] ②当 OB DB BC AB  时 有 BD= 2 2OB AB BC  …………………………………… 7 分 同理可得：BE = DE =2 ，OE = OB-BE =3 - 2=1∵点 D 在 x 轴下方 ∴点 D 的坐标为（ 1 ，- 2 ） 将点 D 的坐标代入 ( 0)y kx k  中，求得 k = - 2∴满足条件的直线 l 的函数解析式为 2y x  ………… 8 分 ∴综上所述满足条件的直线 l 的解析式是： 3y x  或 2y x  ； 点 D 的坐标为（ 3 4 ， 9 4  ）或（ 1 ，- 2 ） 图②