2019-2020学年山东省济南市章丘区九年级（上）期中数学试卷 15页

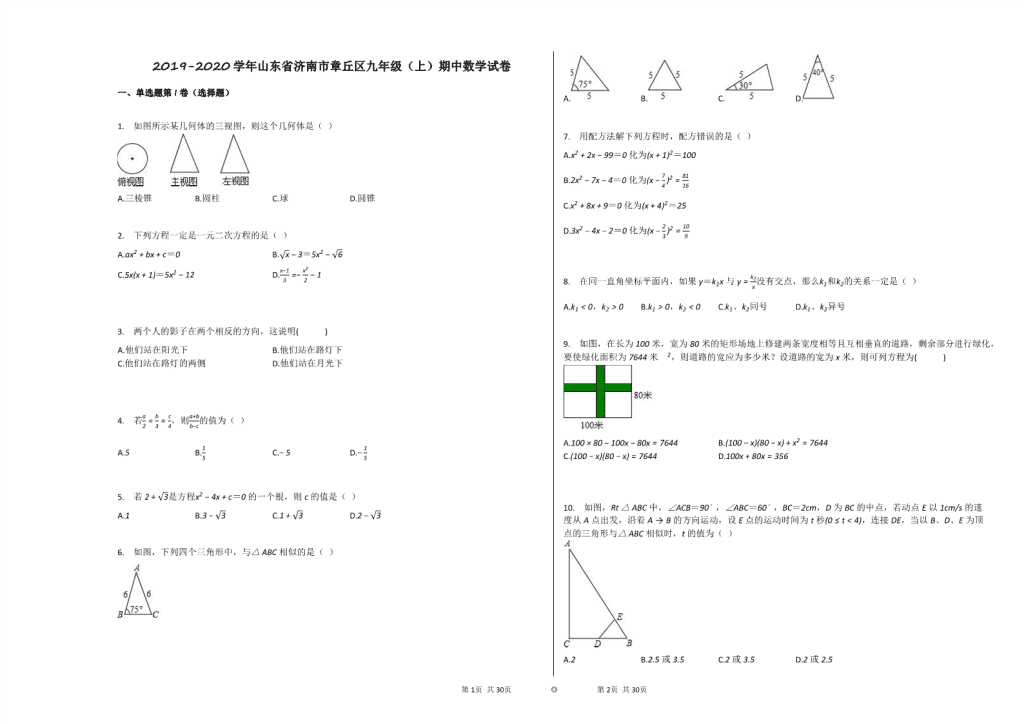
‎2019-2020学年山东省济南市章丘区九年级（上）期中数学试卷 一、单选题第I卷（选择题）‎ ‎ ‎ ‎1. 如图所示某几何体的三视图，则这个几何体是（ ） ‎ A.三棱锥 B.圆柱 C.球 D.圆锥 ‎ ‎ ‎2. 下列方程一定是一元二次方程的是（ ） ‎ A.ax‎2‎+bx+c＝‎0‎ B.x‎−3‎＝‎5x‎2‎−‎‎6‎ C.‎5x(x+1)‎＝‎5x‎2‎−12‎ D.x−1‎‎3‎‎=−x‎2‎‎2‎−1‎ ‎ ‎ ‎ ‎3. 两个人的影子在两个相反的方向，这说明(        ) ‎ A.他们站在阳光下 B.他们站在路灯下 C.他们站在路灯的两侧 D.他们站在月光下 ‎ ‎ ‎ ‎4. 若a‎2‎‎=b‎3‎=‎c‎4‎，则a+bb−c的值为（ ） ‎ A.‎5‎ B.‎1‎‎5‎ C.‎−5‎ D.‎‎−‎‎1‎‎5‎ ‎ ‎ ‎5. 若‎2+‎‎3‎是方程x‎2‎‎−4x+c＝‎0‎的一个根，则c的值是（ ） ‎ A.‎1‎ B.‎3−‎‎3‎ C.‎1+‎‎3‎ D.‎‎2−‎‎3‎ ‎ ‎ ‎6. 如图，下列四个三角形中，与‎△ABC相似的是（ ） ‎ A. B. C. D.‎ ‎ ‎ ‎7. 用配方法解下列方程时，配方错误的是（ ） ‎ A.x‎2‎‎+2x−99‎＝‎0‎化为‎(x+1‎‎)‎‎2‎＝‎‎100‎ B.‎2x‎2‎−7x−4‎＝‎0‎化为‎(x−‎7‎‎4‎)‎‎2‎‎=‎‎81‎‎16‎ C.x‎2‎‎+8x+9‎＝‎0‎化为‎(x+4‎‎)‎‎2‎＝‎‎25‎ D.‎3x‎2‎−4x−2‎＝‎0‎化为‎(x−‎2‎‎3‎)‎‎2‎‎=‎‎10‎‎9‎ ‎ ‎ ‎8. 在同一直角坐标平面内，如果y＝k‎1‎x与y=‎k‎2‎x没有交点，那么k‎1‎和k‎2‎的关系一定是（ ） ‎ A.k‎1‎‎<0‎，k‎2‎‎>0‎ B.k‎1‎‎>0‎，k‎2‎‎<0‎ C.k‎1‎、k‎2‎同号 D.k‎1‎、k‎2‎异号 ‎ ‎ ‎9. 如图，在长为‎100‎米，宽为‎80‎米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为‎7644‎米‎​‎‎2‎，则道路的宽应为多少米？设道路的宽为x米，则可列方程为(        ) ‎ A.‎100×80−100x−80x=7644‎ B.‎(100−x)(80−x)+x‎2‎=7644‎ C.‎(100−x)(80−x)=7644‎ D.‎100x+80x=356‎ ‎ ‎ ‎ ‎10. 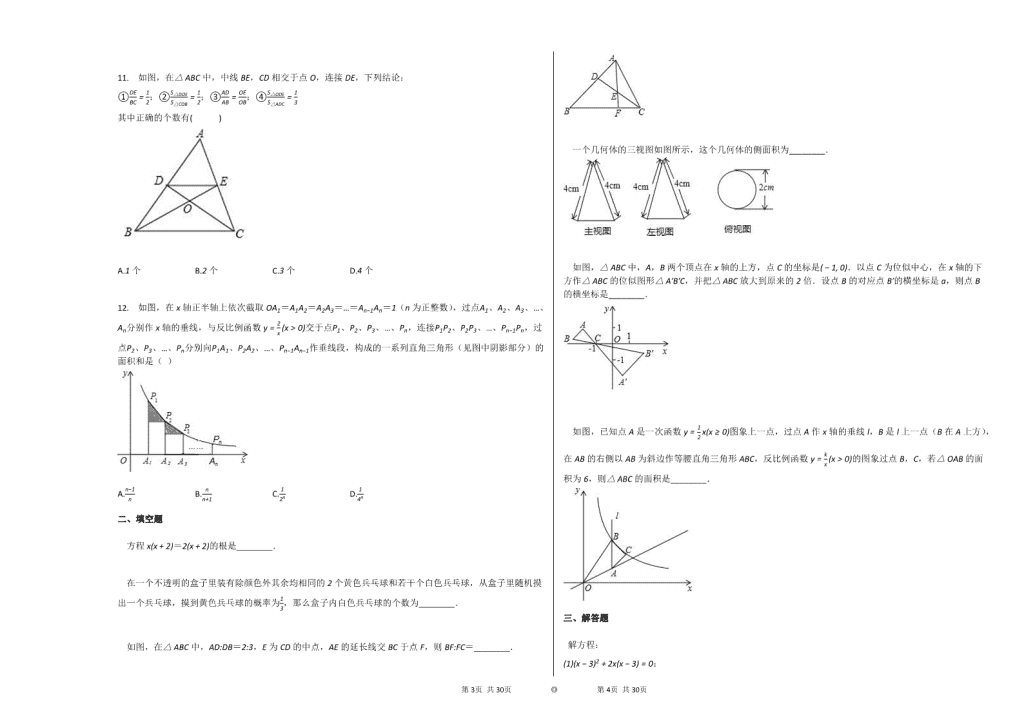如图，Rt△ABC中，‎∠ACB＝‎90‎‎∘‎，‎∠ABC＝‎60‎‎∘‎，BC＝‎2cm，D为BC的中点，若动点E以‎1cm/s的速度从A点出发，沿着A→B的方向运动，设E点的运动时间为t秒‎(0≤t<4)‎，连接DE，当以B、D、E为顶点的三角形与‎△ABC相似时，t的值为（ ） ‎ A.‎2‎ B.‎2.5‎或‎3.5‎ C.‎2‎或‎3.5‎ D.‎2‎或‎2.5‎ 第29页 共30页 ◎ 第30页 共30页 ‎ ‎ ‎11. 如图，在‎△ABC中，中线BE，CD相交于点O，连接DE，下列结论： ①DEBC‎=‎‎1‎‎2‎；②S‎△DOES‎△COB‎=‎‎1‎‎2‎；③ADAB‎=‎OEOB；④S‎△ODES‎△ADC‎=‎‎1‎‎3‎ 其中正确的个数有(        ) ‎ A.‎1‎个 B.‎2‎个 C.‎3‎个 D.‎4‎个 ‎ ‎ ‎12. 如图，在x轴正半轴上依次截取OA‎1‎＝A‎1‎A‎2‎＝A‎2‎A‎3‎＝…＝An−1‎An＝‎1‎（n为正整数），过点A‎1‎、A‎2‎、A‎3‎、…、An分别作x轴的垂线，与反比例函数y=‎2‎x(x>0)‎交于点P‎1‎、P‎2‎、P‎3‎、…、Pn，连接P‎1‎P‎2‎、P‎2‎P‎3‎、…、Pn−1‎Pn，过点P‎2‎、P‎3‎、…、Pn分别向P‎1‎A‎1‎、P‎2‎A‎2‎、…、Pn−1‎An−1‎作垂线段，构成的一系列直角三角形（见图中阴影部分）的面积和是（ ） ‎ A.n−1‎n B.nn+1‎ C.‎1‎‎2‎n D.‎‎1‎‎4‎n 二、填空题 ‎ ‎ ‎ 方程x(x+2)‎＝‎2(x+2)‎的根是________． ‎ ‎ ‎ ‎ 在一个不透明的盒子里装有除颜色外其余均相同的‎2‎个黄色兵乓球和若干个白色兵乓球，从盒子里随机摸出一个兵乓球，摸到黄色兵乓球的概率为‎1‎‎3‎，那么盒子内白色兵乓球的个数为________． ‎ ‎ ‎ ‎ 如图，在‎△ABC中，AD:DB＝‎2:3‎，E为CD的中点，AE的延长线交BC于点F，则BF:FC＝________． ‎ ‎ ‎ ‎ 一个几何体的三视图如图所示，这个几何体的侧面积为________． ‎ ‎ ‎ ‎ 如图，‎△ABC中，A，B两个顶点在x轴的上方，点C的坐标是‎(−1, 0)‎．以点C为位似中心，在x轴的下方作‎△ABC的位似图形‎△A′B′C，并把‎△ABC放大到原来的‎2‎倍．设点B的对应点B′‎的横坐标是a，则点B的横坐标是________． ‎ ‎ ‎ ‎ 如图，已知点A是一次函数y=‎1‎‎2‎x(x≥0)‎图象上一点，过点A作x轴的垂线l，B是l上一点（B在A上方），在AB的右侧以AB为斜边作等腰直角三角形ABC，反比例函数y=kx(x>0)‎的图象过点B，C，若‎△OAB的面积为‎6‎，则‎△ABC的面积是________． ‎ 三、解答题 ‎ ‎ ‎ 解方程： ‎ ‎(1)(x−3‎)‎‎2‎+2x(x−3)=0‎‎；‎ 第29页 共30页 ◎ 第30页 共30页 ‎ ‎ ‎(2)‎‎4x‎2‎−8x−1=0‎‎（用配方法解）．‎ ‎ ‎ ‎ 如图，BD，CE是‎△ABC的高．求证：BA⋅AE＝AC⋅AD． ‎ ‎ ‎ ‎ 已知关于x的一元二次方程mx‎2‎−(m+1)x+1‎＝‎0‎． ‎ ‎（1）求证：此方程总有两个实数根；‎ ‎ ‎ ‎（2）若m为整数，当此方程的两个实数根都是整数时，求m的值．‎ ‎ ‎ ‎ 已知，如图在Rt△ABC中，‎∠B＝‎90‎‎∘‎，AB＝‎6cm，BC＝‎8cm，点P由点A出发沿AB方向向终点点B匀速移动，速度为‎1cm/s，点Q由点B出发沿BC方向向终点点C匀速移动，速度为‎2cm/s．如果动点P，Q同时从A，B出发，当P或Q到达终点时运动停止．几秒后，以Q，B，P为顶点的三角形与‎△ABC相似？ ‎ ‎ ‎ ‎ 某商场销售某种冰箱，每台进货价为‎2500‎元，标价为‎3000‎， ‎ ‎（1）若商场连续两次降价，每次降价的百分率相同，最后以‎2430‎元售出，求每次降价的百分率；‎ ‎ ‎ ‎（2）市场调研表明：当每台售价为‎2900‎元时，平均每天能售出‎8‎台，当每台售价每降‎50‎元时，平均每天就能多售出‎4‎台，若商场要想使这种冰箱的销售利润平均每天达到‎5000‎元，则每台冰箱的定价应为多少元？‎ ‎ ‎ ‎ 如图所示，网格纸中的每个小方格都是边长为‎1‎的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的‎△ABC是格点三角形．在建立平面直角坐标系后，点B的坐标为‎(−1, −1)‎． ‎ ‎（1）把‎△ABC向下平移‎5‎格后得到‎△‎A‎1‎B‎1‎C‎1‎，写出点A‎1‎，B‎1‎，C‎1‎的坐标，并画出‎△‎A‎1‎B‎1‎C‎1‎；‎ ‎ ‎ ‎（2）把‎△ABC绕点O按顺时针方向旋转‎180‎‎∘‎后得到‎△‎A‎2‎B‎2‎C‎2‎，写出点A‎2‎，B‎2‎，C‎2‎的坐标，并画出‎△‎A‎2‎B‎2‎C‎2‎；‎ ‎ ‎ ‎（3）把‎△ABC以点O为位似中心放大得到‎△‎A‎3‎B‎3‎C‎3‎，使放大前后对应线段的比为‎1:2‎，写出点A‎3‎，B‎3‎，C‎3‎的坐标，并画出‎△‎A‎3‎B‎3‎C‎3‎． ‎ ‎ ‎ ‎ 某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况，进行了统计调查．随机调查了某班所有同学最喜欢的节目（每名学生必选且只能选择四类节目中的一类）并将调查结果绘成如下不完整的统计图．根据两图提供的信息，回答下列问题： ‎ ‎（1）最喜欢娱乐类节目的有________人，图中x＝________；‎ ‎ ‎ ‎（2）请补全条形统计图；‎ ‎ ‎ ‎（3）根据抽样调查结果，若该校有‎1800‎名学生，请你估计该校有多少名学生最喜欢娱乐类节目；‎ ‎ ‎ ‎（4）在全班同学中，有甲、乙、丙、丁等同学最喜欢体育类节目，班主任打算从甲、乙、丙、丁‎4‎名同学中选取‎2‎人参加学校组织的体育知识竞赛，请用列表法或树状图求同时选中甲、乙两同学的概率．‎ ‎ ‎ ‎ 提出问题 ‎ ‎(1)‎如图‎1‎，在等边‎△ABC中，点M是BC上任意一点（不含端点B，C），连接AM，以AM为边作等边‎△AMN，连接CN，求证：‎∠ABC=‎‎∠ACN；‎ ‎ ‎ 第29页 共30页 ◎ 第30页 共30页 类比探究 ‎(2)‎如图‎2‎，在等边‎△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，‎(1)‎中的结论‎∠ABC=‎‎∠ACN还成立吗？请说明理由；‎ ‎ ‎ 拓展延伸 ‎(3)‎如图‎3‎，在等腰‎△ABC中，BA=‎BC，点M是BC上的任意一点（不含端点B，C），连结AM，以AM为边作等腰‎△AMN，使顶角‎∠AMN=‎‎∠ABC，连接CN，试探究‎∠ABC与‎∠ACN的数量关系，并说明理由． ‎ ‎ ‎ ‎ 如图‎1‎，已知直线y＝‎3x分别与双曲线y=‎‎12‎x、y=kx(x>0)‎交于P、Q两点，且OP＝‎2OQ． ‎ ‎（1）求k的值．‎ ‎ ‎ ‎（2）如图‎2‎，若点A是双曲线y=‎‎12‎x上的动点，AB // x轴，AC // y轴，分别交双曲线y=kx(x>0)‎于点B、C，连接BC．请你探索在点A运动过程中，‎△ABC的面积是否变化？若不变，请求出‎△ABC的面积；若改变，请说明理由；‎ ‎ ‎ ‎（3）如图‎3‎，若点D是直线y＝‎3x上的一点，请你进一步探索在点A运动过程中，以点A、B、C、D为顶点的四边形能否为平行四边形？若能，求出此时点A的坐标；若不能，请说明理由．‎ 第29页 共30页 ◎ 第30页 共30页 参考答案与试题解析 ‎2019-2020学年山东省济南市章丘区九年级（上）期中数学试卷 一、单选题第I卷（选择题）‎ ‎1.‎ ‎【答案】‎ D ‎【考点】‎ 由三视图判断几何体 ‎【解析】‎ 根据一个空间几何体的主视图和俯视图都是三角形，可判断该几何体是锥体，再根据左视图的形状，即可得出答案．‎ ‎【解答】‎ ‎∵ 几何体的主视图和俯视图都是三角形， ∴ 该几何体是一个锥体， ∵ 俯视图是一个圆， ∴ 该几何体是一个圆锥；‎ ‎2.‎ ‎【答案】‎ D ‎【考点】‎ 一元二次方程的定义 ‎【解析】‎ 根据一元二次方程的定义：未知数的最高次数是‎2‎；二次项系数不为‎0‎；是整式方程；含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．‎ ‎【解答】‎ B‎、x‎−3‎＝‎5x‎2‎−‎‎6‎不是一元二次方程，故选项B不合题意（1）C、‎5x(x+1)‎＝‎5x‎2‎−12‎化简为‎5x+12‎＝‎0‎，是一元一次方程，故选项C不合题意（2）D、x−1‎‎3‎‎=−x‎2‎‎2‎−1‎是一元二次方程，故选项D符合题意（3）故选：D．‎ ‎3.‎ ‎【答案】‎ C ‎【考点】‎ 平行投影 中心投影 ‎【解析】‎ 本题考查中心投影的特点．‎ ‎【解答】‎ 解：根据两个人的影子在两个相反的方向，则一定是中心投影；且两人同在光源两侧． 故选C. ‎ ‎4.‎ ‎【答案】‎ C ‎【考点】‎ 比例的性质 ‎【解析】‎ 设a‎2‎‎=b‎3‎=c‎4‎=k，则a＝‎2k，b＝‎3k，c＝‎4k，然后代入求值即可．‎ ‎【解答】‎ 解：设a‎2‎‎=b‎3‎=c‎4‎=k， 则a‎=‎‎2k，b‎=‎‎3k，c‎=‎‎4k， a+bb−c‎=‎2k+3k‎3k−4k=‎5k‎−k=−5‎. 故选C. ‎ ‎5.‎ ‎【答案】‎ A ‎【考点】‎ 一元二次方程的解 ‎【解析】‎ 把‎2+‎‎3‎代入方程x‎2‎‎−4x+c＝‎0‎就得到关于c的方程，就可以解得c的值．‎ ‎【解答】‎ 把‎2+‎‎3‎代入方程x‎2‎‎−4x+c＝‎0‎，得‎(2+‎3‎‎)‎‎2‎−4(2+‎3‎)+c＝‎0‎， 解得c＝‎1‎；‎ ‎6.‎ ‎【答案】‎ C ‎【考点】‎ 相似三角形的判定 ‎【解析】‎ ‎△ABC是等腰三角形，底角是‎75‎‎∘‎，则顶角是‎30‎‎∘‎，结合各选项是否符合相似的条件即可．‎ ‎【解答】‎ ‎∵ 由图可知，AB＝AC＝‎6‎，‎∠B＝‎75‎‎∘‎， ∴ ‎∠C＝‎75‎‎∘‎，‎∠A＝‎30‎‎∘‎， A、三角形各角的度数分别为‎75‎‎∘‎，‎52.5‎‎∘‎，‎52.5‎‎∘‎， B、三角形各角的度数都是‎60‎‎∘‎， C、三角形各角的度数分别为‎75‎‎∘‎，‎30‎‎∘‎，‎75‎‎∘‎， D、三角形各角的度数分别为‎40‎‎∘‎，‎70‎‎∘‎，‎70‎‎∘‎， ∴ 只有C选项中三角形各角的度数与题干中三角形各角的度数相等，‎ ‎7.‎ ‎【答案】‎ C ‎【考点】‎ 解一元二次方程-配方法 ‎【解析】‎ 第29页 共30页 ◎ 第30页 共30页 根据配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为‎1‎；（3）等式两边同时加上一次项系数一半的平方分别进行配方，即可求出答案．‎ ‎【解答】‎ A‎、由原方程，得x‎2‎‎+2x＝‎99‎， 等式的两边同时加上一次项系数‎2‎的一半的平方‎1‎，得 ‎(x+1‎‎)‎‎2‎＝‎100‎； 故本选项正确； B、由原方程，得 ‎2x‎2‎−7x＝‎4‎， 等式的两边同时加上一次项系数‎−7‎的一半的平方，得， ‎(x−‎7‎‎4‎‎)‎‎2‎=‎‎81‎‎16‎， 故本选项正确； C、由原方程，得 x‎2‎‎+8x＝‎−9‎， 等式的两边同时加上一次项系数‎8‎的一半的平方‎16‎，得 ‎(x+4‎‎)‎‎2‎＝‎7‎； 故本选项错误； D、由原方程，得 ‎3x‎2‎−4x＝‎2‎， 化二次项系数为‎1‎，得 x‎2‎‎−‎4‎‎3‎x=‎‎2‎‎3‎ 等式的两边同时加上一次项系数‎−‎‎4‎‎3‎的一半的平方‎16‎‎9‎，得 ‎(x−‎2‎‎3‎)‎‎2‎‎=‎‎10‎‎9‎； 故本选项正确．‎ ‎8.‎ ‎【答案】‎ D ‎【考点】‎ 反比例函数与一次函数的综合 ‎【解析】‎ 如果直线y＝k‎1‎x与双曲线y=‎k‎2‎x没有交点，则k‎1‎x=‎k‎2‎x无解，即k‎2‎k‎1‎‎<0‎．‎ ‎【解答】‎ ‎∵ 直线y＝k‎1‎x与双曲线y=‎k‎2‎x没有交点， ∴ k‎1‎x=‎k‎2‎x无解， ∴ x‎2‎‎=‎k‎2‎k‎1‎无解， ∴ k‎2‎k‎1‎‎<0‎．即k‎1‎和k‎2‎异号．‎ ‎9.‎ ‎【答案】‎ C ‎【考点】‎ 由实际问题抽象出一元二次方程 一元二次方程的应用--几何图形面积问题 ‎【解析】‎ 把所修的两条道路分别平移到矩形的最上边和最左边，则剩下的草坪是一个长方形，根据长方形的面积公式列方程．‎ ‎【解答】‎ 解：设道路的宽应为x米，由题意有 ‎(100−x)(80−x)=7644‎， 故选C．‎ ‎10.‎ ‎【答案】‎ C ‎【考点】‎ 相似三角形的判定 ‎【解析】‎ 求出AB＝‎2BC＝‎4cm，分两种情况：①当‎∠EDB＝‎∠ACB＝‎90‎‎∘‎时，DE // AC，‎△EBD∽△ABC，得出AE＝BE=‎1‎‎2‎AB＝‎2cm，即可得出t＝‎2s；②当‎∠DEB＝‎∠ACB＝‎90‎‎∘‎时，证出‎△DBE∽△ABC，得出‎∠BDE＝‎∠A＝‎30‎‎∘‎，因此BE=‎1‎‎2‎BD=‎1‎‎2‎cm，得出AE＝‎3.5cm，t＝‎3.5s；即可得出结果．‎ ‎【解答】‎ ‎∵ ，‎∠ACB＝‎90‎‎∘‎，‎∠ABC＝‎60‎‎∘‎， ∴ ‎∠A＝‎30‎‎∘‎， ∴ AB＝‎2BC＝‎4cm， 分两种情况： ①当‎∠EDB＝‎∠ACB＝‎90‎‎∘‎时， DE // AC，‎△EBD∽△ABC， ∵ D为BC的中点， ∴ BD＝CD=‎1‎‎2‎BC＝‎1cm，E为AB的中点，AE＝BE=‎1‎‎2‎AB＝‎2cm， ∴ t＝‎2s； ②当‎∠DEB＝‎∠ACB＝‎90‎‎∘‎时， ∵ ‎∠B＝‎∠B， ∴ ‎△DBE∽△ABC， ∴ ‎∠BDE＝‎∠A＝‎30‎‎∘‎， ∴ BE=‎1‎‎2‎BD=‎1‎‎2‎cm， ∴ AE＝‎3.5cm， ∴ t＝‎3.5s； 综上所述：当以B、D、E为顶点的三角形与‎△ABC相似时，t的值为‎2‎或‎3.5‎；‎ ‎11.‎ ‎【答案】‎ 第29页 共30页 ◎ 第30页 共30页 B ‎【考点】‎ 相似三角形的性质与判定 三角形的重心 ‎【解析】‎ BE‎、CD是‎△ABC的中线，即D、E是AB和AC的中点，即DE是‎△ABC的中位线，则DE // BC，‎△ODE∽△OCB，根据相似三角形的性质即可判断．‎ ‎【解答】‎ 解：∵ BE、CD是‎△ABC的中线，即D、E是AB和AC的中点， ∴ DE是‎△ABC的中位线， ∴ DE=‎1‎‎2‎BC，即DEBC‎=‎‎1‎‎2‎， DE // BC， ∴ ‎△DOE∽△COB， ∴ S‎△DOES‎△COB‎=(DEBC‎)‎‎2‎=(‎1‎‎2‎‎)‎‎2‎=‎‎1‎‎4‎， OEOB‎=DEBC=ADAB=‎‎1‎‎2‎， 故①正确，②错误，③正确； 设‎△ABC的BC边上的高AF，则S‎△ABC‎=‎1‎‎2‎BC⋅AF，S‎△ACD‎=‎1‎‎2‎S‎△ABC=‎1‎‎4‎BC⋅AF， ∵ ‎△ODE中，DE=‎1‎‎2‎BC，DE边上的高是‎1‎‎2‎‎×‎1‎‎3‎AF=‎1‎‎6‎AF， ∴ S‎△ODE‎=‎1‎‎2‎×‎1‎‎2‎BC×‎1‎‎6‎AF=‎1‎‎24‎BC⋅AF， ∴ S‎△ODES‎△ADC‎=‎1‎‎24‎BC⋅AF‎1‎‎4‎BC⋅AF=‎‎1‎‎6‎，故④错误． 故正确的是①③． 故选B．‎ ‎12.‎ ‎【答案】‎ A ‎【考点】‎ 反比例函数系数k的几何意义 ‎【解析】‎ 由OA‎1‎＝A‎1‎A‎2‎＝A‎2‎A‎3‎＝…＝An−1‎An＝‎1‎可知P‎1‎点的坐标为‎(1, y‎1‎)‎，P‎2‎点的坐标为‎(2, y‎2‎)‎，P‎3‎点的坐标为‎(3, y‎3‎)‎…Pn点的坐标为‎(n, yn)‎，把x＝‎1‎，x＝‎2‎，x＝‎3‎代入反比例函数的解析式即可求出y‎1‎、y‎2‎、y‎3‎的值，再由三角形的面积公式可得出S‎1‎、S‎2‎、S‎3‎‎...‎Sn−1‎的值，故可得出结论．‎ ‎【解答】‎ ‎∴ S‎1‎‎=‎1‎‎2‎(1)(3)‎∵ S‎1‎‎=‎1‎‎2‎×1×(y‎1‎−y‎2‎)=‎1‎‎2‎×1×(2−‎2‎‎2‎)‎＝‎1−‎1‎‎2‎(2)‎∴ S‎2‎‎=‎1‎‎2‎×1×(y‎2‎−y‎3‎)=‎1‎‎2‎−‎1‎‎3‎(3)S‎3‎=‎1‎‎2‎×1×(y‎3‎−y‎4‎)=‎1‎‎2‎×(‎2‎‎3‎−‎2‎‎4‎)=‎1‎‎3‎−‎1‎‎4‎(4)‎… ∴ Sn−1‎‎=‎1‎n−1‎−‎‎1‎n， ∴ S‎1‎‎+S‎2‎+S‎3‎+...+Sn−1‎=1−‎1‎‎2‎+‎1‎‎2‎−‎1‎‎3‎+‎1‎‎3‎−‎1‎‎4‎+⋯‎1‎n−1‎−‎1‎n=‎n−1‎n． 故选：A．‎ 二、填空题 ‎【答案】‎ x‎1‎‎＝‎−2‎，x‎2‎＝‎‎2‎ ‎【考点】‎ 解一元二次方程-因式分解法 ‎【解析】‎ 利用提取公因式法，将原式因式分解为‎(x−2)(x+2)‎＝‎0‎，求出即可．‎ ‎【解答】‎ x(x+2)‎‎＝‎2(x+2)‎， ‎(x−2)(x+2)‎＝‎0‎， x−2‎＝‎0‎或x+2‎＝‎0‎， ∴ x‎1‎＝‎2‎，x‎2‎＝‎−2‎；‎ ‎【答案】‎ ‎4‎ ‎【考点】‎ 概率公式 ‎【解析】‎ 先求出盒子内乒乓球的总个数为，然后用总个数减去黄球个数得到据摸到白色乒乓球的个数．‎ ‎【解答】‎ 盒子内乒乓球的个数为‎2÷‎1‎‎3‎=6‎（个）， 白色兵乓球的个数‎6−2‎＝‎4‎（个）‎ ‎【答案】‎ ‎5‎‎2‎ ‎【考点】‎ 平行线分线段成比例 ‎【解析】‎ 根据题意作辅助线，根据已知条件可证明‎△DGE≅△CFE，所以DG＝FC，根据比例关系得知DG // FC，最后根据三角形平行线段成比例关系即可得出答案．‎ ‎【解答】‎ 在AE上取点G，使EG＝EF， ∵ E为CD的中点， ∴ DE＝CE， 又∵ EG＝EF，‎∠DEG＝‎∠CEF， ∴ ‎△DGE≅△CFE， ∴ DG＝FC， 根据比例关系可知：DG // FC， ∵ AD:DB＝‎2:3‎， ∴ ‎ 第29页 共30页 ◎ 第30页 共30页 ‎ BFFC‎=BFDG=ABAD=‎‎5‎‎2‎．‎ ‎【答案】‎ ‎4πcm‎2‎ ‎【考点】‎ 由三视图判断几何体 ‎【解析】‎ 俯视图为圆的只有圆锥，圆柱，球，根据主视图和左视图都是三角形可得到此几何体为圆锥，那么侧面积＝底面周长‎×‎母线长‎÷2‎．‎ ‎【解答】‎ 此几何体为圆锥； ∵ 直径为‎2cm，母线长为‎4cm， ∴ 侧面积＝‎2π×4÷2‎＝‎4π(cm‎2‎)‎．‎ ‎【答案】‎ ‎−‎1‎‎2‎(a+3)‎ ‎【考点】‎ 坐标与图形性质 作图-位似变换 ‎【解析】‎ 设点B的横坐标为x，然后表示出BC、B′C的横坐标的距离，再根据位似比列式计算即可得解．‎ ‎【解答】‎ 设点B的横坐标为x， 则B、C间的横坐标的长度为‎−1−x，B′‎、C间的横坐标的长度为a+1‎， ∵ ‎△ABC放大到原来的‎2‎倍得到‎△A′B′C， ∴ ‎2(−1−x)‎＝a+1‎， 解得x=−‎1‎‎2‎(a+3)‎．‎ ‎【答案】‎ ‎3‎ ‎【考点】‎ 反比例函数系数k的几何意义 等腰直角三角形 反比例函数图象上点的坐标特征 ‎【解析】‎ 本题介绍两种解法： 解法一：设A(t, t‎2‎)‎、B(t, kt)‎，根据反比例函数关于y=x对称可得C(kt, t)‎，得：CE=‎t‎2‎，则DE=t=2CE，则发现‎△ABC和‎△ABO两个三角形是同底边，根据高的倍数可得：S‎△ABO‎=2‎S‎△ABC，可得结论； 解法二：作辅助线，构建直角三角形，设AB=2a，根据直角三角形斜边中线是斜边一半得：BE=AE=CE=a，设A(x, ‎1‎‎2‎x)‎，则B(x, ‎1‎‎2‎x+2a)‎，C(x+a, ‎1‎‎2‎x+a)‎，因为B、C都在反比例函数的图象上，列方程可得结论．‎ ‎【解答】‎ 解法一：设A(t, t‎2‎)‎、B(t, kt)‎， ∵ ‎△ABC是等腰直角三角形，且AB⊥x轴， ∴ 直线BC与y轴夹角为‎45‎度角， 所以根据双曲线的对称性可得，C(kt, t)‎， 过C作CE垂直AB于E，交y轴于D， ∴ AE=yC−yA=t−‎1‎‎2‎t=‎1‎‎2‎t， ∵ ‎△AEC是等腰直角三角形， ∴ CE=AE=‎t‎2‎，则DE=t=2CE， 则S‎△ABO‎=2‎S‎△ABC， ∵ ‎△OAB的面积为‎6‎， ∴ S‎△ABC‎=3‎； 解法二：如图，过C作CD⊥y轴于D，交AB于E， ∵ AB⊥x轴， ∴ CD⊥AB， ∵ ‎△ABC是等腰直角三角形， ∴ BE=AE=CE， 设AB=2a，则BE=AE=CE=a， 设A(x, ‎1‎‎2‎x)‎，则B(x, ‎1‎‎2‎x+2a)‎，C(x+a, ‎1‎‎2‎x+a)‎， ∵ B，C在反比例函数的图象上， ∴ x(‎1‎‎2‎x+2a)=(x+a)(‎1‎‎2‎x+a)‎， x=2a， ∵ S‎△OAB‎=‎1‎‎2‎AB⋅DE=‎1‎‎2‎⋅2a⋅x=6‎， ∴ ax=6‎， ∴ ‎2a‎2‎=6‎， a‎2‎‎=3‎， ∵ S‎△ABC‎=‎1‎‎2‎AB⋅CE=‎1‎‎2‎⋅2a⋅a=a‎2‎=3‎．‎ 三、解答题 ‎【答案】‎ 解：‎(1)(x−3)(x−3+2x)=0‎， 即‎(x−3)(3x−3)=0‎， ∴ x−3=0‎或‎3x−3=0‎， 解得：x=3‎或x=1‎；‎ 第29页 共30页 ◎ 第30页 共30页 ‎(2)‎‎4x‎2‎−8x=1‎‎， x‎2‎‎−2x=‎‎1‎‎4‎， x‎2‎‎−2x+1=‎1‎‎4‎+1‎，即‎(x−1‎)‎‎2‎=‎‎5‎‎4‎， ∴ x−1=±‎‎5‎‎2‎， ∴ x=1±‎‎5‎‎2‎．‎ ‎【考点】‎ 解一元二次方程-因式分解法 解一元二次方程-配方法 ‎【解析】‎ ‎（1）因式分解法求解可得；‎ ‎（2）配方法求解可得．‎ ‎【解答】‎ 解：‎(1)(x−3)(x−3+2x)=0‎， 即‎(x−3)(3x−3)=0‎， ∴ x−3=0‎或‎3x−3=0‎， 解得：x=3‎或x=1‎；‎ ‎(2)‎‎4x‎2‎−8x=1‎‎， x‎2‎‎−2x=‎‎1‎‎4‎， x‎2‎‎−2x+1=‎1‎‎4‎+1‎，即‎(x−1‎)‎‎2‎=‎‎5‎‎4‎， ∴ x−1=±‎‎5‎‎2‎， ∴ x=1±‎‎5‎‎2‎．‎ ‎【答案】‎ ‎∵ BD，CE是‎△ABC的高 ∴ ‎∠ADB＝‎∠AEC＝‎90‎‎∘‎ 又∵ ‎∠A＝‎∠A ∴ ‎△ADB∽△AEC ∴ ADAE‎=‎ABAC ∴ AD⋅AC＝AE⋅AB 即BA⋅AE＝AC⋅AD．‎ ‎【考点】‎ 相似三角形的性质与判定 ‎【解析】‎ 根据有两个角相等的三角形是相似三角形，判定‎△ADB∽△AEC，再根据相似三角形的性质得出比例式，再将比例式写成乘积形式即可得证．‎ ‎【解答】‎ ‎∵ BD，CE是‎△ABC的高 ∴ ‎∠ADB＝‎∠AEC＝‎90‎‎∘‎ 又∵ ‎∠A＝‎∠A ∴ ‎△ADB∽△AEC ∴ ADAE‎=‎ABAC ∴ AD⋅AC＝AE⋅AB 即BA⋅AE＝AC⋅AD．‎ ‎【答案】‎ 证明：‎△‎＝‎[−(m+1)‎]‎‎2‎−4m＝‎(m−1‎‎)‎‎2‎． ∵ ‎(m−1‎)‎‎2‎≥0‎， ∴ ‎△≥0‎． ∴ 该方程总有两个实数根；‎ x=‎‎(m+1)±‎‎(m−1‎‎)‎‎2‎‎2m‎． ∴ x‎1‎＝‎1‎，x‎2‎‎=‎‎1‎m． 当m为整数‎1‎或‎−1‎时，x‎2‎为整数，即该方程的两个实数根都是整数， ∴ m的值为‎1‎或‎−1‎．‎ ‎【考点】‎ 根的判别式 解一元二次方程-公式法 ‎【解析】‎ ‎（1）表示出一元二次方程根的判别式，利用配方化成完全平方式，可判定其不小于‎0‎，可得出结论； （2）可先用求根公式表示出两根，再根据方程的根都是整数，可求得m的值．‎ ‎【解答】‎ 证明：‎△‎＝‎[−(m+1)‎]‎‎2‎−4m＝‎(m−1‎‎)‎‎2‎． ∵ ‎(m−1‎)‎‎2‎≥0‎， ∴ ‎△≥0‎． ∴ 该方程总有两个实数根；‎ x=‎‎(m+1)±‎‎(m−1‎‎)‎‎2‎‎2m‎． ∴ x‎1‎＝‎1‎，x‎2‎‎=‎‎1‎m． 当m为整数‎1‎或‎−1‎时，x‎2‎为整数，即该方程的两个实数根都是整数， ∴ m的值为‎1‎或‎−1‎．‎ ‎【答案】‎ 设t秒后，以Q，B，P为顶点的三角形与‎△ABC相似； 则PB＝‎(6−t)cm，BQ＝‎2tcm， ∵ ‎∠B＝‎90‎‎∘‎， ∴ 分两种情况： ①当PBAB‎=‎BQBC时， 即‎6−t‎6‎‎=‎‎2t‎8‎， 解得：t＝‎2.4‎； ②当PBBC‎=‎BQAB时， 即‎6−t‎8‎‎=‎‎2t‎6‎， 解得：t=‎‎18‎‎11‎； 综上所述：‎2.4‎秒或‎18‎‎11‎秒时，以Q，B，‎P 第29页 共30页 ◎ 第30页 共30页 为顶点的三角形与‎△ABC相似．‎ ‎【考点】‎ 相似三角形的判定 ‎【解析】‎ 设t秒后，以Q，B，P为顶点的三角形与‎△ABC相似；则PB＝‎(6−t)cm，BQ＝‎2tcm，分两种情况：①当PBAB‎=‎BQBC时；②当PBBC‎=‎BQAB时；分别解方程即可得出结果．‎ ‎【解答】‎ 设t秒后，以Q，B，P为顶点的三角形与‎△ABC相似； 则PB＝‎(6−t)cm，BQ＝‎2tcm， ∵ ‎∠B＝‎90‎‎∘‎， ∴ 分两种情况： ①当PBAB‎=‎BQBC时， 即‎6−t‎6‎‎=‎‎2t‎8‎， 解得：t＝‎2.4‎； ②当PBBC‎=‎BQAB时， 即‎6−t‎8‎‎=‎‎2t‎6‎， 解得：t=‎‎18‎‎11‎； 综上所述：‎2.4‎秒或‎18‎‎11‎秒时，以Q，B，P为顶点的三角形与‎△ABC相似．‎ ‎【答案】‎ 设每次降价的百分率为x， 依题意得：‎3000(1−x‎)‎‎2‎＝‎2430‎， 解得x‎1‎＝‎0.1‎＝‎10%‎，x‎2‎＝‎1.9‎（不合题意，舍去） 答：每次降价的百分率是‎10%‎；‎ 假设下调a个‎50‎元，依题意得：‎5000‎＝‎(400−50a)(8+4a)‎． 解得a＝‎3‎． 所以下调‎150‎元，因此定价为‎2750‎元．‎ ‎【考点】‎ 一元二次方程的应用 ‎【解析】‎ ‎（1）设每次降价的百分率为x，根据降价后的价格＝降价前的价格（‎1−‎降价的百分率），则第一次降价后的价格是‎60(1−x)‎元，第二次后的价格是‎60(1−x‎)‎‎2‎元，据此即可列方程求解； （2）假设下调a个‎50‎元，销售利润＝一台冰箱的利润‎×‎销售冰箱数量，一台冰箱的利润＝售价-进价，降低售价的同时，销售量就会提高，“一减一加”，根据每台的盈利‎×‎销售的件数＝‎5000‎元，即可列方程求解．‎ ‎【解答】‎ 设每次降价的百分率为x， 依题意得：‎3000(1−x‎)‎‎2‎＝‎2430‎， 解得x‎1‎＝‎0.1‎＝‎10%‎，x‎2‎＝‎1.9‎（不合题意，舍去） 答：每次降价的百分率是‎10%‎；‎ 假设下调a个‎50‎元，依题意得：‎5000‎＝‎(400−50a)(8+4a)‎． 解得a＝‎3‎． 所以下调‎150‎元，因此定价为‎2750‎元．‎ ‎【答案】‎ 如图所示，‎△‎A‎1‎B‎1‎C‎1‎即为所求： 点A‎1‎，B‎1‎，C‎1‎的坐标分别为‎(3, −2)‎，‎(−1, −6)‎，‎‎(5, −6)‎ 如图所示‎△‎A‎2‎B‎2‎C‎2‎即为所求： 点A‎2‎，B‎2‎，C‎2‎的坐标分别为‎(−3, −3)‎，‎(1, 1)‎，‎(−5, 1)‎；‎ 如图所示‎△‎A‎3‎B‎3‎C‎3‎即为所求： 点A‎3‎，B‎3‎，C‎3‎的坐标分别为‎(6, 6)‎，‎(−2, −2)‎，‎(10, −2)‎或‎(−6, −6)‎，‎(2, 2)‎，‎(−10, 2)‎．‎ ‎【考点】‎ 作图-位似变换 作图-旋转变换 作图－平移变换 ‎【解析】‎ ‎（1）直接利用平移的性质得出对应点位置进而得出答案； （2）直接利用旋转的性质得出对应点位置进而得出答案； （3）直接利用位似图形的性质得出对应点位置进而得出答案．‎ ‎【解答】‎ 如图所示，‎△‎A‎1‎B‎1‎C‎1‎即为所求： 点A‎1‎，B‎1‎，C‎1‎的坐标分别为‎(3, −2)‎，‎(−1, −6)‎，‎‎(5, −6)‎ 第29页 共30页 ◎ 第30页 共30页 如图所示‎△‎A‎2‎B‎2‎C‎2‎即为所求： 点A‎2‎，B‎2‎，C‎2‎的坐标分别为‎(−3, −3)‎，‎(1, 1)‎，‎(−5, 1)‎；‎ 如图所示‎△‎A‎3‎B‎3‎C‎3‎即为所求： 点A‎3‎，B‎3‎，C‎3‎的坐标分别为‎(6, 6)‎，‎(−2, −2)‎，‎(10, −2)‎或‎(−6, −6)‎，‎(2, 2)‎，‎(−10, 2)‎．‎ ‎【答案】‎ ‎20‎‎,‎‎18‎ 补全条形图如下： ‎ 估计该校最喜欢娱乐类节目的学生有‎1800×‎20‎‎50‎=720‎（人）；‎ 画树状图得： ∵ 共有‎12‎种等可能的结果，恰好同时选中甲、乙两位同学的有‎2‎种情况， ∴ 恰好同时选中甲、乙两位同学的概率为‎2‎‎12‎‎=‎‎1‎‎6‎．‎ ‎【考点】‎ 用样本估计总体 条形统计图 列表法与树状图法 ‎【解析】‎ ‎（1）先根据“新闻”类人数及其所占百分比求得总人数，再用总人数减去其他三个类型人数即可求得“娱乐”类人数，用“动画”类人数除以总人数可得x的值； （2）根据（1）中所求结果即可补全条形图； （3）总人数乘以样本中“娱乐”类节目人数所占比例； （4）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好同时选中甲、乙两位同学的情况，然后利用概率公式求解即可求得答案．‎ ‎【解答】‎ ‎∵ 被调查的总人数为‎6÷12%‎＝‎50‎人， ∴ 最喜欢娱乐类节目的有‎50−(6+15+9)‎＝‎20‎，x%=‎9‎‎50‎×100%‎＝‎18%‎，即x＝‎18‎， 故答案为：‎20‎、‎18‎；‎ 补全条形图如下： ‎ 估计该校最喜欢娱乐类节目的学生有‎1800×‎20‎‎50‎=720‎（人）；‎ 画树状图得： ∵ 共有‎12‎种等可能的结果，恰好同时选中甲、乙两位同学的有‎2‎种情况， ∴ 恰好同时选中甲、乙两位同学的概率为‎2‎‎12‎‎=‎‎1‎‎6‎．‎ ‎【答案】‎ ‎(1)‎证明：∵ ‎△ABC，‎△AMN是等边三角形， ∴ AB=‎AC，AM=‎AN，‎∠BAC=‎‎∠MAN=‎‎60‎‎∘‎， ∴ ‎∠BAM=‎‎∠CAN. ∵ 在‎△BAM和‎△CAN中， AB=AC，‎‎∠BAM=∠CAN，‎AM=AN，‎‎ ‎ ∴ ‎△BAM≅△CAN(SAS)‎， ∴ ‎∠ABC=‎‎∠ACN．‎ ‎(2)‎解：结论‎∠ABC=‎‎∠ACN仍成立，理由如下： ∵ ‎△ABC，‎△AMN是等边三角形， ∴ AB=‎AC，AM=‎AN，‎∠BAC=‎‎∠MAN=‎‎60‎‎∘‎， ∴ ‎∠BAM＝‎∠CAN. ∵ 在‎△BAM和‎△CAN中， AB=AC，‎‎∠BAM=∠CAN，‎AM=AN，‎‎ ‎ ∴ ‎△BAM≅△CAN(SAS)‎， ∴ ‎∠ABC=‎‎∠ACN．‎ ‎(3)‎解：‎∠ABC=‎‎∠ACN. 理由如下：∵ BA=‎BC，MA=‎MN， 顶角‎∠ABC=‎‎∠AMN， ∴ 底角‎∠BAC=‎‎∠MAN， ∴ ‎△ABC∼△AMN， ∴ ABAC‎=‎AMAN. 又∵ ‎∠BAM=‎‎∠BAC−∠MAC， ‎∠CAN=‎‎∠MAN−∠MAC， ∴ ‎∠BAM=‎‎∠CAN， ∴ ‎△BAM∼△CAN， ∴ ‎ 第29页 共30页 ◎ 第30页 共30页 ‎ ‎∠ABC=‎‎∠ACN．‎ ‎【考点】‎ 相似三角形的性质与判定 全等三角形的性质与判定 等边三角形的性质 ‎【解析】‎ ‎（1）利用SAS可证明‎△BAM≅△CAN，继而得出结论； （2）也可以通过证明‎△BAM≅△CAN，得出结论，和（1）的思路完全一样． （3）首先得出‎∠BAC＝‎∠MAN，从而判定‎△ABC∽△AMN，得到ABAM‎=‎ACAN，根据‎∠BAM＝‎∠BAC−∠MAC，‎∠CAN＝‎∠MAN−∠MAC，得到‎∠BAM＝‎∠CAN，从而判定‎△BAM∽△CAN，得出结论．‎ ‎【解答】‎ ‎(1)‎证明：∵ ‎△ABC，‎△AMN是等边三角形， ∴ AB=‎AC，AM=‎AN，‎∠BAC=‎‎∠MAN=‎‎60‎‎∘‎， ∴ ‎∠BAM=‎‎∠CAN. ∵ 在‎△BAM和‎△CAN中， AB=AC，‎‎∠BAM=∠CAN，‎AM=AN，‎‎ ‎ ∴ ‎△BAM≅△CAN(SAS)‎， ∴ ‎∠ABC=‎‎∠ACN．‎ ‎(2)‎解：结论‎∠ABC=‎‎∠ACN仍成立，理由如下： ∵ ‎△ABC，‎△AMN是等边三角形， ∴ AB=‎AC，AM=‎AN，‎∠BAC=‎‎∠MAN=‎‎60‎‎∘‎， ∴ ‎∠BAM＝‎∠CAN. ∵ 在‎△BAM和‎△CAN中， AB=AC，‎‎∠BAM=∠CAN，‎AM=AN，‎‎ ‎ ∴ ‎△BAM≅△CAN(SAS)‎， ∴ ‎∠ABC=‎‎∠ACN．‎ ‎(3)‎解：‎∠ABC=‎‎∠ACN. 理由如下：∵ BA=‎BC，MA=‎MN， 顶角‎∠ABC=‎‎∠AMN， ∴ 底角‎∠BAC=‎‎∠MAN， ∴ ‎△ABC∼△AMN， ∴ ABAC‎=‎AMAN. 又∵ ‎∠BAM=‎‎∠BAC−∠MAC， ‎∠CAN=‎‎∠MAN−∠MAC， ∴ ‎∠BAM=‎‎∠CAN， ∴ ‎△BAM∼△CAN， ∴ ‎∠ABC=‎‎∠ACN．‎ ‎【答案】‎ 过点Q作QE⊥x轴，垂足为E，过点P作PF⊥x轴，垂足为F，如图‎1‎， 联立y=3xy=‎‎12‎x‎ ‎， 解得：x=−2‎y=−6‎‎ ‎或x=2‎y=6‎‎ ‎， ∵ x>0‎， ∴ 点P的坐标为‎(2, 6)‎， ∴ OF＝‎2‎，PF＝‎6‎， ∵ QE⊥x轴，PF⊥x轴， ∴ QE // PF， ∴ ‎△OEQ∽△OFP， ∴ OEOF‎=EQFP=‎OQOP， ∵ OP＝‎2OQ， ∴ OF＝‎2OE＝‎2‎，PF＝‎2EQ＝‎6‎， ∴ OE＝‎1‎，EQ＝‎3‎， ∴ 点Q的坐标为‎(1, 3)‎， ∵ 点Q(1, 3)‎在双曲线y=‎kx上， ∴ k＝‎1×3‎＝‎3‎， ∴ k的值为；‎ 第29页 共30页 ◎ 第30页 共30页 如图‎2‎， 设点A的坐标为‎(a, b)‎， ∵ 点A(a, b)‎在双曲线y=‎‎12‎x上， ∴ b=‎‎12‎a． ∵ ．AB // x轴，AC // y轴， ∴ xC＝xA＝a，yB＝yA＝b=‎‎12‎a． ∵ 点B、C在双曲线y=‎‎3‎x上， ∴ xB‎=‎3‎‎12‎a=‎a‎4‎，yC‎=‎‎3‎a． ∴ 点B的坐标为‎(a‎4‎, ‎12‎a)‎，点C的坐标为‎(a, ‎3‎a)‎． ∴ AB＝a−a‎4‎=‎‎3a‎4‎，AC=‎12‎a−‎3‎a=‎‎9‎a． ∴ S‎△ABC‎=‎1‎‎2‎AB⋅AC ‎=‎1‎‎2‎×‎3a‎4‎×‎‎9‎a ‎=‎‎27‎‎8‎． ∴ 在点A运动过程中，‎△ABC的面积不变，始终等于‎27‎‎8‎；‎ 第29页 共30页 ◎ 第30页 共30页 ‎①AC为平行四边形的一边， Ⅰ．当点B在点Q的右边时，如图‎3‎， ∵ 四边形ACBD是平行四边形， ∴ AC // BD，AC＝BD． ∴ xD＝xB‎=‎a‎4‎． ∴ yD＝‎3xD=‎‎3a‎4‎ ∴ DB=‎3a‎4‎−‎‎12‎a， ∵ AC=‎12‎a−‎2‎a=‎‎10‎a， ∴ ‎10‎a‎=a‎2‎−‎‎12‎a． 解得：a＝‎±2 ‎‎7‎． 经检验：a＝‎±2 ‎‎7‎是该方程的解． ∵ a>0‎， ∴ a＝‎2 ‎‎7‎． ∴ b=‎12‎a=‎‎6‎‎7‎‎7‎． ∴ 点A的坐标为‎(2 ‎7‎, ‎6‎‎7‎‎7‎)‎； Ⅱ．当点B在点Q的左边且点C在点Q的右边时，如图‎4‎， ∵ 四边形ACDB是平行四边形， ∴ AC // BD，AC＝BD， ∴ xD＝xB‎=‎a‎4‎． ∴ yD＝‎3xD=‎‎3a‎4‎， ∴ DB=‎12‎a−‎‎3a‎4‎， ∵ AC=‎‎9‎a， ∴ ‎9‎a‎=‎3a‎4‎−‎‎12‎a， 解得：a＝‎±2‎． 经检验：a＝‎±2‎是该方程的解． ∵ a>0‎， ∴ a＝‎2‎． ∴ b=‎12‎a=6‎， ∴ 点A的坐标为‎(2, 6)‎， ②AC为平行四边形的对角线， 此时点B、点C都在点Q的左边，如图‎5‎， ∵ 四边形ABCD是平行四边形， ∴ AB // CD，AB＝CD． ∴ yD＝yC‎=‎‎3‎a ∴ xD‎=yD‎3‎=‎‎1‎a． ∴ CD=‎1‎a−a． ∵ AB＝a−a‎4‎=‎‎3a‎4‎， ∴ ‎3a‎4‎‎=‎1‎a−a． 解得：a＝‎±‎‎2‎‎7‎‎7‎． 经检验：a＝‎±‎‎2‎‎7‎‎7‎是该方程的解． ∵ a>0‎， ∴ a=‎‎2‎‎7‎‎7‎， ∴ b=‎12‎a=6‎‎7‎， ∴ 点A的坐标为‎( ‎2‎‎7‎‎7‎, 6‎7‎)‎． 综上所述：当点A、B、C、D为顶点的四边形为平行四边形时，此时点A的坐标为‎(2 ‎7‎, ‎6‎‎7‎‎7‎)‎或‎(2, 6)‎或‎( ‎2‎‎7‎‎7‎, 6‎7‎)‎． ‎ ‎【考点】‎ 反比例函数综合题 ‎【解析】‎ ‎（1）先求出点P的坐标，再从条件OP＝‎2OQ出发，构造相似三角形，求出点Q的坐标，就可求出k的值． （2）设点A的坐标为‎(a, b)‎，易得b=‎‎12‎a，结合条件可用a的代数式表示点B、点C的坐标，进而表示出线段AB、AC的长，就可算出‎△BAC的面积是一个定值． （3）以点A、B、C、D为顶点的四边形为平行四边形可分成两类：①AC为平行四边形的一边，②AC为平行四边形的对角线；然后利用平行四边形的性质建立关于a的方程，即可求出a的值，从而求出点A的坐标．‎ ‎【解答】‎ 过点Q作QE⊥x轴，垂足为E，过点P作PF⊥x轴，垂足为F，如图‎1‎， 联立y=3xy=‎‎12‎x‎ ‎， 解得：x=−2‎y=−6‎‎ ‎或x=2‎y=6‎‎ ‎， ∵ x>0‎， ∴ 点P的坐标为‎(2, 6)‎， ∴ OF＝‎2‎，PF＝‎6‎， ∵ QE⊥x轴，PF⊥x轴， ∴ QE // PF， ∴ ‎△OEQ∽△OFP， ∴ OEOF‎=EQFP=‎OQOP， ∵ OP＝‎2OQ， ∴ OF＝‎2OE＝‎2‎，PF＝‎2EQ＝‎6‎， ∴ OE＝‎1‎，EQ＝‎3‎， ∴ 点Q的坐标为‎(1, 3)‎， ∵ 点Q(1, 3)‎在双曲线y=‎kx上， ∴ k＝‎1×3‎＝‎3‎， ∴ k的值为；‎ 如图‎2‎， 设点A的坐标为‎(a, b)‎， ∵ 点A(a, b)‎在双曲线y=‎‎12‎x上， ∴ b=‎‎12‎a． ∵ ．AB // x轴，AC // y轴， ∴ xC＝xA＝a，yB＝yA＝b=‎‎12‎a． ∵ 点B、C在双曲线y=‎‎3‎x上， ∴ xB‎=‎3‎‎12‎a=‎a‎4‎，yC‎=‎‎3‎a． ∴ 点B的坐标为‎(a‎4‎, ‎12‎a)‎，点C的坐标为‎(a, ‎3‎a)‎． ∴ AB＝a−a‎4‎=‎‎3a‎4‎，AC=‎12‎a−‎3‎a=‎‎9‎a． ∴ S‎△ABC‎=‎1‎‎2‎AB⋅AC ‎=‎1‎‎2‎×‎3a‎4‎×‎‎9‎a ‎=‎‎27‎‎8‎． ∴ 在点A运动过程中，‎△ABC的面积不变，始终等于‎27‎‎8‎；‎ ‎①AC为平行四边形的一边， Ⅰ．当点B在点Q的右边时，如图‎3‎， ∵ 四边形ACBD是平行四边形， ∴ AC // BD，AC＝BD． ∴ xD＝xB‎=‎a‎4‎． ∴ yD＝‎3xD=‎‎3a‎4‎ ∴ DB=‎3a‎4‎−‎‎12‎a， ∵ AC=‎12‎a−‎2‎a=‎‎10‎a， ∴ ‎10‎a‎=a‎2‎−‎‎12‎a． 解得：a＝‎±2 ‎‎7‎． 经检验：a＝‎±2 ‎‎7‎是该方程的解． ∵ a>0‎， ∴ a＝‎2 ‎‎7‎． ∴ b=‎12‎a=‎‎6‎‎7‎‎7‎． ∴ 点A的坐标为‎(2 ‎7‎, ‎6‎‎7‎‎7‎)‎； Ⅱ．当点B在点Q的左边且点C在点Q的右边时，如图‎4‎， ∵ 四边形ACDB是平行四边形， ∴ AC // BD，AC＝BD， ∴ xD＝xB‎=‎a‎4‎． ∴ yD＝‎3xD=‎‎3a‎4‎， ∴ DB=‎12‎a−‎‎3a‎4‎， ∵ ‎ 第29页 共30页 ◎ 第30页 共30页 ‎ AC=‎‎9‎a， ∴ ‎9‎a‎=‎3a‎4‎−‎‎12‎a， 解得：a＝‎±2‎． 经检验：a＝‎±2‎是该方程的解． ∵ a>0‎， ∴ a＝‎2‎． ∴ b=‎12‎a=6‎， ∴ 点A的坐标为‎(2, 6)‎， ②AC为平行四边形的对角线， 此时点B、点C都在点Q的左边，如图‎5‎， ∵ 四边形ABCD是平行四边形， ∴ AB // CD，AB＝CD． ∴ yD＝yC‎=‎‎3‎a ∴ xD‎=yD‎3‎=‎‎1‎a． ∴ CD=‎1‎a−a． ∵ AB＝a−a‎4‎=‎‎3a‎4‎， ∴ ‎3a‎4‎‎=‎1‎a−a． 解得：a＝‎±‎‎2‎‎7‎‎7‎． 经检验：a＝‎±‎‎2‎‎7‎‎7‎是该方程的解． ∵ a>0‎， ∴ a=‎‎2‎‎7‎‎7‎， ∴ b=‎12‎a=6‎‎7‎， ∴ 点A的坐标为‎( ‎2‎‎7‎‎7‎, 6‎7‎)‎． 综上所述：当点A、B、C、D为顶点的四边形为平行四边形时，此时点A的坐标为‎(2 ‎7‎, ‎6‎‎7‎‎7‎)‎或‎(2, 6)‎或‎( ‎2‎‎7‎‎7‎, 6‎7‎)‎． ‎ 第29页 共30页 ◎ 第30页 共30页