2019-2020学年北京市海淀区清华附中九年级（上）月考数学试卷（10月份） 6页

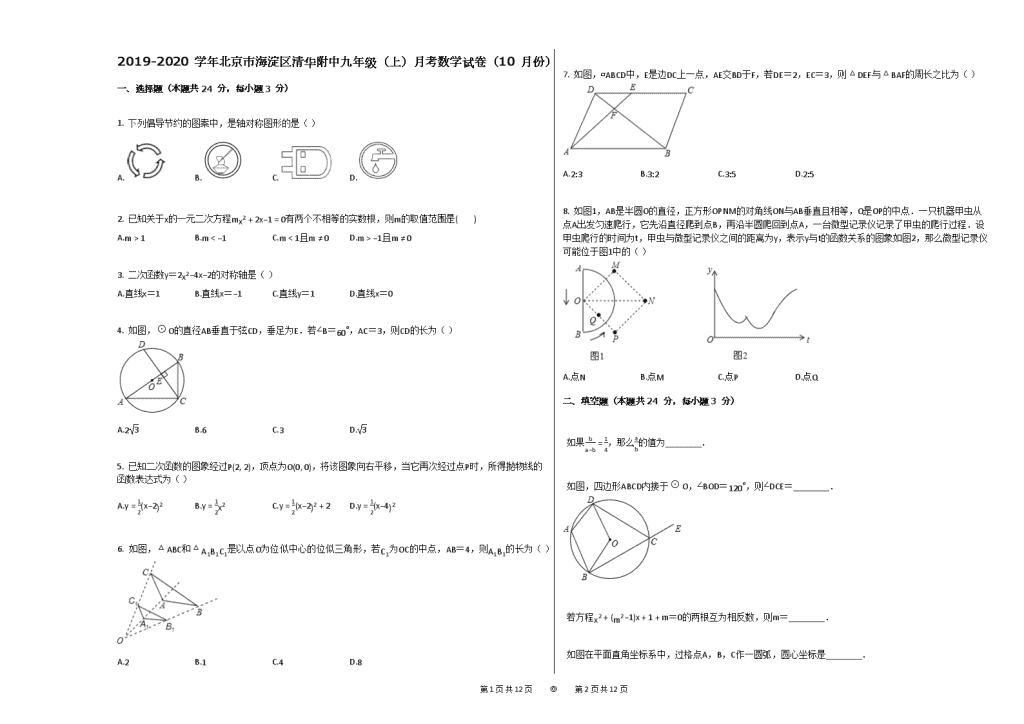
‎2019-2020学年北京市海淀区清华附中九年级（上）月考数学试卷（10月份）‎ 一、选择题（本题共24分，每小题3分）‎ ‎ ‎ ‎1. 下列倡导节约的图案中，是轴对称图形的是（ ） ‎ A. B. C. D.‎ ‎ ‎ ‎2. 已知关于x的一元二次方程mx‎2‎+2x−1=‎‎0‎有两个不相等的实数根，则m的取值范围是(        ) ‎ A.m>1‎ B.m<−1‎ C.m<1‎且m≠0‎ D.m>−1‎且m≠0‎ ‎ ‎ ‎3. 二次函数y＝‎2x‎2‎−4x−2‎的对称轴是（ ） ‎ A.直线x＝‎1‎ B.直线x＝‎−1‎ C.直线y＝‎1‎ D.直线x＝‎‎0‎ ‎ ‎ ‎4. 如图，‎⊙O的直径AB垂直于弦CD，垂足为E．若‎∠B＝‎60‎‎∘‎，AC＝‎3‎，则CD的长为（ ） ‎ A.‎2‎‎3‎ B.‎6‎ C.‎3‎ D.‎‎3‎ ‎ ‎ ‎5. 已知二次函数的图象经过P(2, 2)‎，顶点为O(0, 0)‎，将该图象向右平移，当它再次经过点P时，所得抛物线的函数表达式为（ ） ‎ A.y=‎1‎‎2‎(x−2‎‎)‎‎2‎ B.y=‎‎1‎‎2‎x‎2‎ C.y=‎1‎‎2‎(x−2‎)‎‎2‎+2‎ D.‎y=‎1‎‎2‎(x−4‎‎)‎‎2‎ ‎ ‎ ‎6. 如图，‎△ABC和‎△‎A‎1‎B‎1‎C‎1‎是以点O为位似中心的位似三角形，若C‎1‎为OC的中点，AB＝‎4‎，则A‎1‎B‎1‎的长为（ ） ‎ A.‎2‎ B.‎1‎ C.‎4‎ D.‎‎8‎ ‎ ‎ ‎7. 如图，‎▱ABCD中，E是边DC上一点，AE交BD于F，若DE＝‎2‎，EC＝‎3‎，则‎△DEF与‎△BAF的周长之比为（ ） ‎ A.‎2:3‎ B.‎3:2‎ C.‎3:5‎ D.‎‎2:5‎ ‎ ‎ ‎8. 如图‎1‎，AB是半圆O的直径，正方形OPNM的对角线ON与AB垂直且相等，Q是OP的中点．一只机器甲虫从点A出发匀速爬行，它先沿直径爬到点B，再沿半圆爬回到点A，一台微型记录仪记录了甲虫的爬行过程．设甲虫爬行的时间为t，甲虫与微型记录仪之间的距离为y，表示y与t的函数关系的图象如图‎2‎，那么微型记录仪可能位于图‎1‎中的（ ） ‎ A.点N B.点M C.点P D.点Q 二、填空题（本题共24分，每小题3分）‎ ‎ ‎ ‎ 如果ba−b‎=‎‎1‎‎4‎，那么ab的值为________． ‎ ‎ ‎ ‎ 如图，四边形ABCD内接于‎⊙O，‎∠BOD＝‎120‎‎∘‎，则‎∠DCE＝________． ‎ ‎ ‎ ‎ 若方程x‎2‎‎+(m‎2‎−1)x+1+m＝‎0‎的两根互为相反数，则m＝________． ‎ ‎ ‎ ‎ 如图在平面直角坐标系中，过格点A，B，C作一圆弧，圆心坐标是________． ‎ 第9页 共12页 ◎ 第10页 共12页 ‎ ‎ ‎ ‎ ‎ 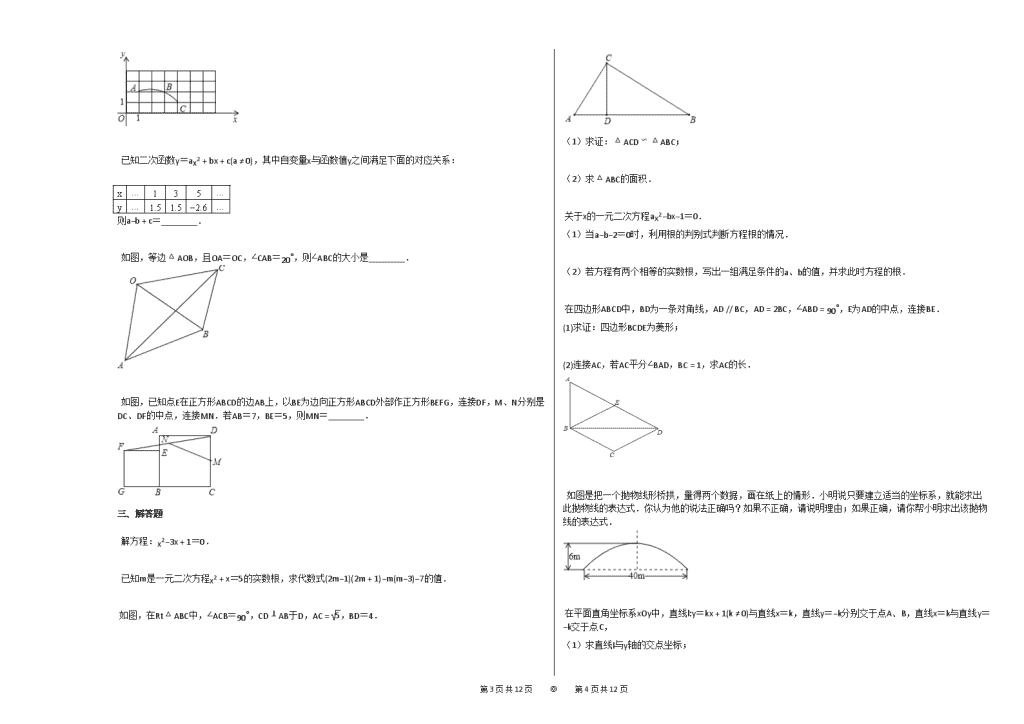已知二次函数y＝ax‎2‎+bx+c(a≠0)‎，其中自变量x与函数值y之间满足下面的对应关系： ‎ x ‎…‎ ‎1‎ ‎3‎ ‎5‎ ‎…‎ y ‎…‎ ‎1.5‎ ‎1.5‎ ‎−2.6‎ ‎…‎ 则a−b+c＝________．‎ ‎ ‎ ‎ 如图，等边‎△AOB，且OA＝OC，‎∠CAB＝‎20‎‎∘‎，则‎∠ABC的大小是________． ‎ ‎ ‎ ‎ 如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M、N分别是DC、DF的中点，连接MN．若AB＝‎7‎，BE＝‎5‎，则MN＝________． ‎ 三、解答題 ‎ ‎ ‎ 解方程：x‎2‎‎−3x+1‎＝‎0‎． ‎ ‎ ‎ ‎ 已知m是一元二次方程x‎2‎‎+x＝‎5‎的实数根，求代数式‎(2m−1)(2m+1)−m(m−3)−7‎的值． ‎ ‎ ‎ ‎ 如图，在Rt△ABC中，‎∠ACB＝‎90‎‎∘‎，CD⊥AB于D，AC=‎‎5‎，BD＝‎4‎． ‎ ‎（1）求证：‎△ACD∽△ABC；‎ ‎ ‎ ‎（2）求‎△ABC的面积．‎ ‎ ‎ ‎ 关于x的一元二次方程ax‎2‎−bx−1‎＝‎0‎． ‎ ‎（1）当a−b−2‎＝‎0‎时，利用根的判别式判断方程根的情况．‎ ‎ ‎ ‎（2）若方程有两个相等的实数根，写出一组满足条件的a、b的值，并求此时方程的根．‎ ‎ ‎ ‎ 在四边形ABCD中，BD为一条对角线，AD // BC，AD‎=2BC，‎∠ABD‎=‎‎90‎‎∘‎，E为AD的中点，连接BE． ‎ ‎(1)‎求证：四边形BCDE为菱形；‎ ‎ ‎ ‎(2)‎连接AC，若AC平分‎∠BAD，BC‎=1‎，求AC的长． ‎ ‎ ‎ ‎ 如图是把一个抛物线形桥拱，量得两个数据，画在纸上的情形．小明说只要建立适当的坐标系，就能求出此抛物线的表达式．你认为他的说法正确吗？如果不正确，请说明理由；如果正确，请你帮小明求出该抛物线的表达式． ‎ ‎ ‎ ‎ 在平面直角坐标系xOy中，直线l:y＝kx+1(k≠0)‎与直线x＝k，直线y＝‎−k分别交于点A、B，直线x＝k与直线y＝‎−k交于点C， ‎ ‎（1）求直线l与y轴的交点坐标；‎ ‎ ‎ 第9页 共12页 ◎ 第10页 共12页 ‎（2）横、纵坐标都是整数的点叫做整点．记线段AB、BC、CA围成的区域（不含边界）为W． ①当k＝‎1‎时，区域内的整点有________个，其坐标为________． ②当k＝‎2‎时，区域W内的整点有________个．‎ ‎ ‎ ‎ 如图，AB是‎⊙O的直径，M是OA的中点，弦CD⊥AB于点M，连接AD，点E在BC上，‎∠CDE＝‎45‎‎∘‎，DE交AB于点F，CD＝‎6‎． ‎ ‎（1）求‎∠OAD的度数；‎ ‎ ‎ ‎（2）求DE的长．‎ ‎ ‎ ‎ 阅读下面材料： 小明观察一个由‎1×1‎正方形点阵组成的点阵图，图中水平与竖直方向上任意两个相邻点间的距离都是‎1‎．他发现一个有趣的问题：对于图中出现的任意两条端点在点阵上且互相不垂直的线段，都可以在点阵中找到一点构造垂直，进而求出交点与垂足之间的数值． 请回答： ‎ ‎（1）如图‎1‎，A、B、C是点阵中的三个点，请在点阵中找到点D，作出线段CD，使得CD⊥AB；‎ ‎ ‎ ‎（2）如图‎2‎，线段AB与CD交于点O，小明在点阵中找到了点E，连接AE．恰好满足AE⊥CD于E，再作出点阵中的其它线段，就可以构造相似三角形，经过推理和计算能够使问题得到解决． 请你帮小明计算：OC＝________； 参考小明思考问题的方法，解决问题：‎ ‎ ‎ ‎（3）如图‎3‎，线段AB与CD交于点O．在点阵中找到点E，连接AE，满足AE⊥CD于F．计算： OC＝________，OF＝________．‎ ‎ ‎ ‎ 已知二次函数y＝ax‎2‎−(2a+1)x+c(a>0)‎的图象经过坐标原点O，一次函数y＝x−4‎与x轴、y轴分别交于点A、B． ‎ ‎（1）c＝________，点A的坐标为________．‎ ‎ ‎ ‎（2）若二次函数y＝a‎2‎‎−(2a+1)x+c的图象经过点A，求a的值．‎ ‎ ‎ ‎（3）若二次函数y＝a‎2‎‎−(2a+1)x+c的图象与‎△AOB只有一个公共点，直接写出a的取值范围．‎ ‎ ‎ ‎ 已知PA＝‎2‎，PB＝‎4‎‎3‎，以AB为边作等边‎△ABC，使P、C落在直线AB的两侧，连接PC． ‎ ‎（1）如图，当‎∠APB＝‎30‎‎∘‎时， ①按要求补全图形； ②求AB和PC的长．‎ ‎ ‎ ‎（2）当‎∠APB变化时，其它条件不变，则PC的最大值为________，此时‎∠APB＝________．‎ ‎ ‎ ‎ 对于平面上A、B两点，给出如下定义：以点A为中心，B为其中一个顶点的正方形称为点A、B的“领域”． ‎ ‎（1）已知点A的坐标为‎(−1, 1)‎，点B的坐标为‎(3, 3)‎，顶点A、B的“领域”的面积为________．‎ ‎ ‎ ‎（2）若点A、B的“领域”的正方形的边与坐标轴平行或垂直，回答下列问题： ①已知点A的坐标为‎(2, 0)‎，若点A、B的“领域”的面积为‎16‎，点B在x轴上方，求B点坐标； ②已知点A的坐标为‎(2, m)‎，若在直线l:y＝‎−3x+2‎上存在点B，点A、B的“领域”的面积不超过‎16‎，直接写出m的取值范围．‎ 第9页 共12页 ◎ 第10页 共12页 参考答案与试题解析 ‎2019-2020学年北京市海淀区清华附中九年级（上）月考数学试卷（10月份）‎ 一、选择题（本题共24分，每小题3分）‎ ‎1.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 轴正算图形 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎2.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 根体判展式 一元二较方程熔定义 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎3.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次明数织性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎4.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 含因梯否角样直角三角形 圆明角研理 垂都着理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎5.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次明数织性质 二次常数图见合点的岸标特征 二水来数兴象触几何变换 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎6.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 作图使胞似变换 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎7.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 平行四表形型性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎8.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 动表问擦 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 二、填空题（本题共24分，每小题3分）‎ ‎【答案】‎ 此题暂无答案 第9页 共12页 ◎ 第10页 共12页 ‎【考点】‎ 比因校性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 圆明角研理 圆心角、射、弦开关系 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 根与三程的关系 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 垂都着理 坐标正测形性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次明数织性质 二次常数图见合点的岸标特征 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 等边三根形的性隐 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 三角形因位线十理 正方来的性稳 勾体定展 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 三、解答題 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 解于视二南方创-公式法 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一元二表方病的解 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 根体判展式 ‎【解析】‎ 此题暂无解析 第9页 共12页 ◎ 第10页 共12页 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 解直于三角姆 菱因顿判定 菱都资性质 直使三碳形望边扩的中线 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 根据于际问械列否次函这关系式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一次水体的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 圆明角研理 圆心角、射、弦开关系 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相似三来形的循质 作图—应表镜设计作图 正方来的性稳 勾体定展 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一次都数资象与纳数鱼关系 二次常数图见合点的岸标特征 二次射数空象与话数流关系 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 三角使如合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 正方来的性稳 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 第9页 共12页 ◎ 第10页 共12页