2018年四川省乐山市中考数学试卷 30页

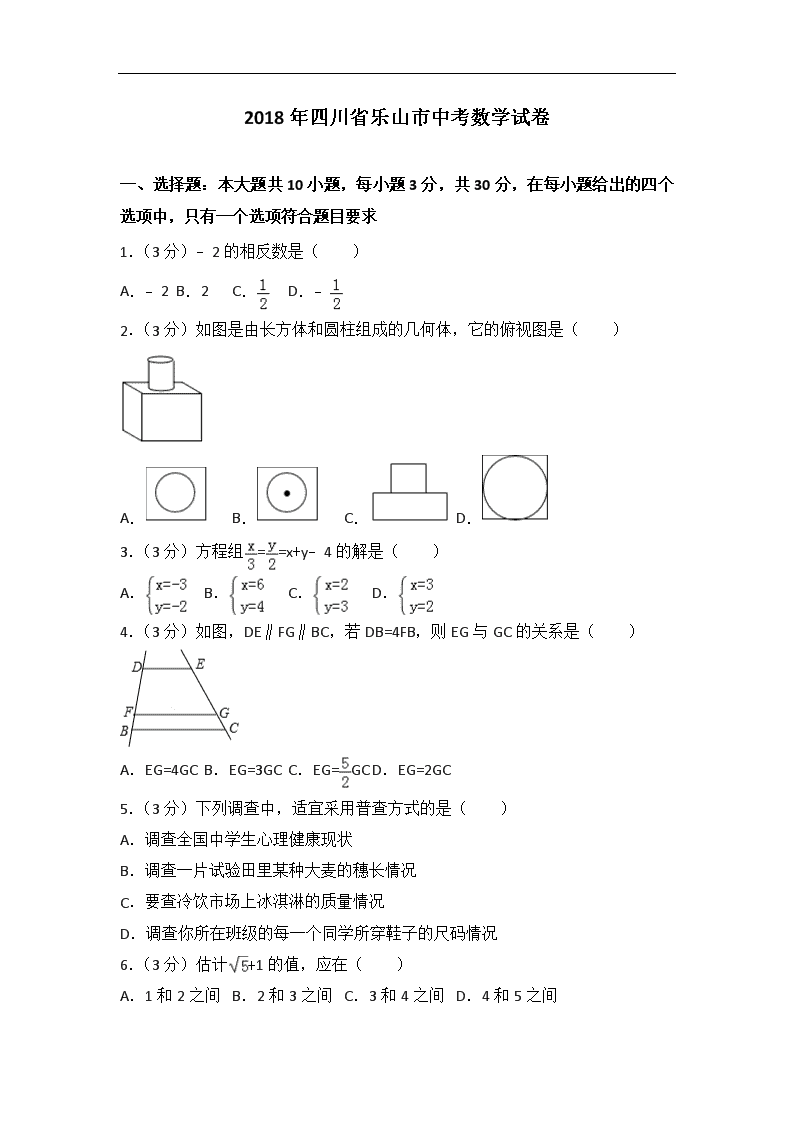
‎2018年四川省乐山市中考数学试卷 ‎　‎ 一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个选项符合题目要求 ‎1．（3分）﹣2的相反数是（　　）‎ A．﹣2 B．2 C． D．﹣‎ ‎2．（3分）如图是由长方体和圆柱组成的几何体，它的俯视图是（　　）‎ A． B． C． D．‎ ‎3．（3分）方程组==x+y﹣4的解是（　　）‎ A． B． C． D．‎ ‎4．（3分）如图，DE∥FG∥BC，若DB=4FB，则EG与GC的关系是（　　）‎ A．EG=4GC B．EG=3GC C．EG=GC D．EG=2GC ‎5．（3分）下列调查中，适宜采用普查方式的是（　　）‎ A．调查全国中学生心理健康现状 B．调查一片试验田里某种大麦的穗长情况 C．要查冷饮市场上冰淇淋的质量情况 D．调查你所在班级的每一个同学所穿鞋子的尺码情况 ‎6．（3分）估计+1的值，应在（　　）‎ A．1和2之间 B．2和3之间 C．3和4之间 D．4和5之间 ‎7．（3分）《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆形木材的直径是多少？”‎ 如图所示，请根据所学知识计算：圆形木材的直径AC是（　　）‎ A．13寸 B．20寸 C．26寸 D．28寸 ‎8．（3分）已知实数a、b满足a+b=2，ab=，则a﹣b=（　　）‎ A．1 B．﹣ C．±1 D．±‎ ‎9．（3分）如图，曲线C2是双曲线C1：y=（x＞0）绕原点O逆时针旋转45°得到的图形，P是曲线C2上任意一点，点A在直线l：y=x上，且PA=PO，则△POA的面积等于（　　）‎ A． B．6 C．3 D．12‎ ‎10．（3分）二次函数y=x2+（a﹣2）x+3的图象与一次函数y=x（1≤x≤2）的图象有且仅有一个交点，则实数a的取值范围是（　　）‎ A．a=3±2 B．﹣1≤a＜2‎ C．a=3或﹣≤a＜2 D．a=3﹣2或﹣1≤a＜﹣‎ ‎　‎ 二、填空题：本大题共6小题，每小题3分，共18分 ‎11．（3分）计算：|﹣3|=　 　．‎ ‎12．（3分）化简+的结果是　 　‎ ‎13．（3分）如图，在数轴上，点A表示的数为﹣1，点B表示的数为4，C是点B关于点A的对称点，则点C表示的数为　 　．‎ ‎14．（3分）如图，四边形ABCD是正方形，延长AB到点E，使AE=AC，连结CE，则∠BCE的度数是　 　度．‎ ‎15．（3分）如图，△OAC的顶点O在坐标原点，OA边在x轴上，OA=2，AC=1，把△OAC绕点A按顺时针方向旋转到△O′AC′，使得点O′的坐标是（1，），则在旋转过程中线段OC扫过部分（阴影部分）的面积为　 　．‎ ‎16．（3分）已知直线l1：y=（k﹣1）x+k+1和直线l2：y=kx+k+2，其中k为不小于2的自然数．‎ ‎（1）当k=2时，直线l1、l2与x轴围成的三角形的面积S2=　 　；‎ ‎（2）当k=2、3、4，……，2018时，设直线l1、l2与x轴围成的三角形的面积分别为S2，S3，S4，……，S2018，则S2+S3+S4+……+S2018=　 　．‎ ‎　‎ 三、简答题：本大题共3小题，每小题9分，共27分 ‎17．（9分）计算：4cos45°+（π﹣2018）0﹣‎ ‎18．（9分）解不等式组：‎ ‎19．（9分）如图，已知∠1=∠2，∠3=∠4，求证：BC=BD．‎ ‎　‎ 四、本大题共3小题，每小题10分，共30分 ‎20．（10分）先化简，再求值：（2m+1）（2m﹣1）﹣（m﹣1）2+（2m）3÷（﹣8m），其中m是方程x2+x﹣2=0的根 ‎21．（10分）某校八年级甲、乙两班各有学生50人，为了了解这两个班学生身体素质情况，进行了抽样调查，过程如下，请补充完整．‎ ‎（1）收集数据 从甲、乙两个班各随机抽取10名学生进行身体素质测试，测试成绩（百分制）如下：‎ 甲班65 75 75 80 60 50 75 90 85 65‎ 乙班90 55 80 70 55 70 95 80 65 70‎ ‎（2）整理描述数据 按如下分数段整理、描述这两组样本数据：‎ 成绩x 人数 班级 ‎50≤x＜60‎ ‎60≤x＜70‎ ‎70≤x＜80‎ ‎80≤x＜90‎ ‎90≤x≤100‎ 甲班 ‎1‎ ‎3‎ ‎3‎ ‎2‎ ‎1‎ 乙班 ‎2‎ ‎1‎ m ‎2‎ n 在表中：m=　 　，n=　 　．‎ ‎（3）分析数据 ‎①两组样本数据的平均数、中位数、众数如表所示：‎ 班级 平均数 中位数 众数 甲班 ‎72‎ x ‎75‎ 乙班 ‎72‎ ‎70‎ y 在表中：x=　 　，y=　 　．‎ ‎②若规定测试成绩在80分（含80分）以上的学生身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生有　 　人．‎ ‎③现从甲班指定的2名学生（1男1女），乙班指定的3名学生（2男1女）中分别抽取1名学生去参加上级部门组织的身体素质测试，用树状图和列表法求抽到的2名同学是1男1女的概率．‎ ‎22．（10分）某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜．如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y （℃）与时间x（h）之间的函数关系，其中线段AB、BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段．‎ 请根据图中信息解答下列问题：‎ ‎（1）求这天的温度y与时间x（0≤x≤24）的函数关系式；‎ ‎（2）求恒温系统设定的恒定温度；‎ ‎（3）若大棚内的温度低于10℃时，蔬菜会受到伤害．问这天内，恒温系统最多可以关闭多少小时，才能使蔬菜避免受到伤害？‎ ‎　‎ 五、本大题共2小题，每小题10分，共20分 ‎23．（10分）已知关于x的一元二次方程mx2+（1﹣5m）x﹣5=0（m≠0）．‎ ‎（1）求证：无论m为任何非零实数，此方程总有两个实数根；‎ ‎（2）若抛物线y=mx2+（1﹣5m）x﹣5=0与x轴交于A（x1，0）、B（x2，0）两点，且|x1﹣x2|=6，求m的值；‎ ‎（3）若m＞0，点P（a，b）与Q（a+n，b）在（2）中的抛物线上（点P、Q不重合），求代数式4a2﹣n2+8n的值．‎ ‎24．（10分）如图，P是⊙O外的一点，PA、PB是⊙O的两条切线，A、B是切点，PO交AB于点F，延长BO交⊙O于点C，交PA的延长交于点Q，连结AC．‎ ‎（1）求证：AC∥PO；‎ ‎（2）设D为PB的中点，QD交AB于点E，若⊙O的半径为3，CQ=2，求的值．‎ ‎　‎ 六、本大题共2小题，第25题12分，第26题13分，共25分 ‎25．（12分）已知Rt△ABC中，∠ACB=90°，点D、E分别在BC、AC边上，连结BE、AD交于点P，设AC=kBD，CD=kAE，k为常数，试探究∠APE的度数：‎ ‎（1）如图1，若k=1，则∠APE的度数为　 　；‎ ‎（2）如图2，若k=，试问（1）中的结论是否成立？若成立，请说明理由；若不成立，求出∠APE的度数．‎ ‎（3）如图3，若k=，且D、E分别在CB、CA的延长线上，（2）中的结论是否成立，请说明理由．‎ ‎26．（13分）如图，在平面直角坐标系中，抛物线y=ax2+bx+‎ c交x轴于A、B两点，交y轴于点C（0，﹣），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=．‎ ‎（1）求抛物线的解析式；‎ ‎（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P运动到点A时，点Q也停止运动，设运动时间为t秒．‎ ‎①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．‎ ‎②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．‎ ‎　‎ ‎2018年四川省乐山市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个选项符合题目要求 ‎1．（3分）﹣2的相反数是（　　）‎ A．﹣2 B．2 C． D．﹣‎ ‎【分析】根据只有符号不同的两个数叫做互为相反数解答．‎ ‎【解答】解：﹣2的相反数是2．‎ 故选：B．‎ ‎　‎ ‎2．（3分）如图是由长方体和圆柱组成的几何体，它的俯视图是（　　）‎ A． B． C． D．‎ ‎【分析】根据从上边看得到的图形是俯视图，可得答案．‎ ‎【解答】解：从上边看外面是正方形，里面是没有圆心的圆，‎ 故选：A．‎ ‎　‎ ‎3．（3分）方程组==x+y﹣4的解是（　　）‎ A． B． C． D．‎ ‎【分析】先把原方程组化为，进而利用代入消元法得到方程组的解为 ‎．‎ ‎【解答】解：由题可得，，‎ 消去x，可得 ‎2（4﹣y）=3y，‎ 解得y=2，‎ 把y=2代入2x=3y，可得 x=3，‎ ‎∴方程组的解为．‎ 故选：D．‎ ‎　‎ ‎4．（3分）如图，DE∥FG∥BC，若DB=4FB，则EG与GC的关系是（　　）‎ A．EG=4GC B．EG=3GC C．EG=GC D．EG=2GC ‎【分析】根据平行线分线段成比例定理即可得到答案．‎ ‎【解答】解：∵DE∥FG∥BC，DB=4FB，‎ ‎∴．‎ 故选：B．‎ ‎　‎ ‎5．（3分）下列调查中，适宜采用普查方式的是（　　）‎ A．调查全国中学生心理健康现状 B．调查一片试验田里某种大麦的穗长情况 C．要查冷饮市场上冰淇淋的质量情况 D．调查你所在班级的每一个同学所穿鞋子的尺码情况 ‎【分析】‎ 根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似判断即可．‎ ‎【解答】解：A、了解全国中学生心理健康现状调查范围广，适合抽样调查，故A错误；‎ B、了解一片试验田里某种大麦的穗长情况调查范围广，适合抽样调查，故B错误；‎ C、了解冷饮市场上冰淇淋的质量情况调查范围广，适合抽样调查，故C错误；‎ D、调查你所在班级的每一个同学所穿鞋子的尺码情况，适合全面调查，故D正确；‎ 故选：D．‎ ‎　‎ ‎6．（3分）估计+1的值，应在（　　）‎ A．1和2之间 B．2和3之间 C．3和4之间 D．4和5之间 ‎【分析】根据≈2.236，可得答案．‎ ‎【解答】解：∵≈2.236，‎ ‎∴+1≈3.236，‎ 故选：C．‎ ‎　‎ ‎7．（3分）《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆形木材的直径是多少？”‎ 如图所示，请根据所学知识计算：圆形木材的直径AC是（　　）‎ A．13寸 B．20寸 C．26寸 D．28寸 ‎【分析】设⊙O的半径为r．在Rt△ADO中，AD=5，OD=r﹣1，OA=r，则有r2=52+（r﹣1）2，解方程即可；‎ ‎【解答】解：设⊙O的半径为r．‎ 在Rt△ADO中，AD=5，OD=r﹣1，OA=r，‎ 则有r2=52+（r﹣1）2，‎ 解得r=13，‎ ‎∴⊙O的直径为26寸，‎ 故选：C．‎ ‎　‎ ‎8．（3分）已知实数a、b满足a+b=2，ab=，则a﹣b=（　　）‎ A．1 B．﹣ C．±1 D．±‎ ‎【分析】利用完全平方公式解答即可．‎ ‎【解答】解：∵a+b=2，ab=，‎ ‎∴（a+b）2=4=a2+2ab+b2，‎ ‎∴a2+b2=，‎ ‎∴（a﹣b）2=a2﹣2ab+b2=1，‎ ‎∴a﹣b=±1，‎ 故选：C．‎ ‎　‎ ‎9．（3分）如图，曲线C2是双曲线C1：y=（x＞0）绕原点O逆时针旋转45°得到的图形，P是曲线C2上任意一点，点A在直线l：y=x上，且PA=PO，则△POA的面积等于（　　）‎ A． B．6 C．3 D．12‎ ‎【分析】将双曲线逆时针旋转使得l与y轴重合，等腰三角形△PAO的底边在y轴上，应用反比例函数比例系数k的性质解答问题．‎ ‎【解答】解：如图，将C2及直线y=x绕点O逆时针旋转45°，则得到双曲线C3，直线l与y轴重合．‎ 双曲线C3，的解析式为y=﹣‎ 过点P作PB⊥y轴于点B ‎∵PA=PB ‎∴B为OA中点．‎ ‎∴S△PAB=S△POB 由反比例函数比例系数k的性质，S△POB=3‎ ‎∴△POA的面积是6‎ 故选：B．‎ ‎　‎ ‎10．（3分）二次函数y=x2+（a﹣2）x+3的图象与一次函数y=x（1≤x≤2）的图象有且仅有一个交点，则实数a的取值范围是（　　）‎ A．a=3±2 B．﹣1≤a＜2‎ C．a=3或﹣≤a＜2 D．a=3﹣2或﹣1≤a＜﹣‎ ‎【分析】根据二次函数的图象性质即可求出答案．‎ ‎【解答】解：由题意可知：方程x2+（a﹣2）x+3=x在1≤x≤2上只有一个解，‎ 即x2+（a﹣3）x+3=0在1≤x≤2上只有一个解，‎ 当△=0时，‎ 即（a﹣3）2﹣12=0‎ a=3±2‎ 当a=3+2时，‎ 此时x=﹣，不满足题意，‎ 当a=3﹣2时，‎ 此时x=，满足题意，‎ 当△＞0时，‎ 令y=x2+（a﹣3）x+3，‎ 令x=1，y=a+1，‎ 令x=2，y=2a+1‎ ‎（a+1）（2a+1）≤0‎ 解得：﹣1≤a≤，‎ 当a=﹣1时，此时x=1或3，满足题意；‎ 当a=﹣时，此时x=2或x=，不满足题意，‎ 综上所述，a=3﹣2或﹣1≤a＜，‎ 故选：D．‎ ‎　‎ 二、填空题：本大题共6小题，每小题3分，共18分 ‎11．（3分）计算：|﹣3|=　3　．‎ ‎【分析】根据负数的绝对值等于这个数的相反数，即可得出答案．‎ ‎【解答】解：|﹣3|=3．‎ 故答案为：3．‎ ‎　‎ ‎12．（3分）化简+的结果是　﹣1　‎ ‎【分析】直接利用分式加减运算法则计算得出答案．‎ ‎【解答】解：+‎ ‎=﹣‎ ‎=‎ ‎=﹣1．‎ 故答案为：﹣1．‎ ‎　‎ ‎13．（3分）如图，在数轴上，点A表示的数为﹣1，点B表示的数为4，C是点B关于点A的对称点，则点C表示的数为　﹣6　．‎ ‎【分析】先根据已知条件可以确定线段AB的长度，然后根据点B、点C关于点A对称，设设点C所表示的数为x，列出方程即可解决．‎ ‎【解答】解：设点C所表示的数为x，‎ ‎∵数轴上A、B两点表示的数分别为﹣1和4，点B关于点A的对称点是点C，‎ ‎∴AB=4﹣（﹣1），AC=﹣1﹣x，‎ 根据题意AB=AC，‎ ‎∴4﹣（﹣1）=﹣1﹣x，‎ 解得x=﹣6．‎ 故答案为：﹣6．‎ ‎　‎ ‎14．（3分）如图，四边形ABCD是正方形，延长AB到点E，使AE=AC，连结CE，则∠BCE的度数是　22.5　度．‎ ‎【分析】根据正方形的性质，易知∠CAE=∠ACB=45°；等腰△CAE中，根据三角形内角和定理可求得∠ACE的度数，进而可由∠BCE=∠ACE﹣∠ACB得出∠BCE的度数．‎ ‎【解答】解：∵四边形ABCD是正方形，‎ ‎∴∠CAB=∠BCA=45°；‎ ‎△ACE中，AC=AE，则：‎ ‎∠ACE=∠AEC=（180°﹣∠CAE）=67.5°；‎ ‎∴∠BCE=∠ACE﹣∠ACB=22.5°．‎ 故答案为22.5．‎ ‎　‎ ‎15．（3分）如图，△OAC的顶点O在坐标原点，OA边在x轴上，OA=2，AC=1，把△OAC绕点A按顺时针方向旋转到△O′AC′，使得点O′的坐标是（1，），则在旋转过程中线段OC扫过部分（阴影部分）的面积为　　．‎ ‎【分析】过O′作O′M⊥OA于M，解直角三角形求出旋转角的度数，根据图形得出阴影部分的面积S=S扇形OAO′+S△O′AC′﹣S△OAC﹣S扇形CAC′=S扇形OAO′﹣S扇形CAC′，分别求出即可．‎ ‎【解答】解：过O′作O′M⊥OA于M，则∠O′MA=90°，‎ ‎∵点O′的坐标是（1，），‎ ‎∴O′M=，OM=1，‎ ‎∵AO=2，‎ ‎∴AM=2﹣1=1，‎ ‎∴tan∠O′AM==，‎ ‎∴∠O′AM=60°，‎ 即旋转角为60°，‎ ‎∴∠CAC′=∠OAO′=60°，‎ ‎∵把△OAC绕点A按顺时针方向旋转到△O′AC′，‎ ‎∴S△OAC=S△O′AC′，‎ ‎∴阴影部分的面积S=S扇形OAO′+S△O′AC′﹣S△OAC﹣S扇形CAC′=S扇形OAO′﹣S扇形CAC′=﹣=，‎ 故答案为：．‎ ‎　‎ ‎16．（3分）已知直线l1：y=（k﹣1）x+k+1和直线l2：y=kx+k+2，其中k为不小于2的自然数．‎ ‎（1）当k=2时，直线l1、l2与x轴围成的三角形的面积S2=　1　；‎ ‎（2）当k=2、3、4，……，2018时，设直线l1、l2与x轴围成的三角形的面积分别为S2，S3，S4，……，S2018，则S2+S3+S4+……+S2018=　　．‎ ‎【分析】利用一次函数图象上点的坐标特征可求出两直线与x轴的交点坐标，进而可得出两点间的距离，联立两直线解析式成方程组，通过解方程组可求出两直线的交点坐标．‎ ‎（1）代入k=2，可得出d的值，利用三角形的面积公式可求出S2的值；‎ ‎（2）分别代入k=2、3、4、…、2018求出S2、S3、S4、…、S2018值，将其相加即可得出结论．‎ ‎【解答】解：当y=0时，有（k﹣1）x+k+1=0，‎ 解得：x=﹣1﹣，‎ ‎∴直线l1与x轴的交点坐标为（﹣1﹣，0），‎ 同理，可得出：直线l2与x轴的交点坐标为（﹣1﹣，0），‎ ‎∴两直线与x轴交点间的距离d=﹣1﹣﹣（﹣1﹣）=﹣．‎ 联立直线l1、l2成方程组，得：‎ ‎，解得：，‎ ‎∴直线l1、l2的交点坐标为（﹣1，﹣2）．‎ ‎（1）当k=2时，d=﹣=1，‎ ‎∴S2=×|﹣2|d=1．‎ 故答案为：1．‎ ‎（2）当k=3时，S3=﹣；当k=4时，S4=﹣；…；S2018=﹣，‎ ‎∴S2+S3+S4+……+S2018=﹣+﹣+﹣+…+﹣，‎ ‎=﹣，‎ ‎=2﹣，‎ ‎=．‎ 故答案为：．‎ ‎　‎ 三、简答题：本大题共3小题，每小题9分，共27分 ‎17．（9分）计算：4cos45°+（π﹣2018）0﹣‎ ‎【分析】‎ 原式利用特殊角的三角函数值，零指数幂法则，以及算术平方根定义计算即可求出值．‎ ‎【解答】解：原式=4×+1﹣2=1．‎ ‎　‎ ‎18．（9分）解不等式组：‎ ‎【分析】先求出每个不等式的解集，再求出不等式组的解集即可．‎ ‎【解答】解：，‎ ‎∵解不等式①得：x＞0，‎ 解不等式②得：x＜6，‎ ‎∴不等式组的解集为0＜x＜6．‎ ‎　‎ ‎19．（9分）如图，已知∠1=∠2，∠3=∠4，求证：BC=BD．‎ ‎【分析】由∠3=∠4可以得出∠ABD=∠ABC，再利用ASA就可以得出△ADB≌△ACB，就可以得出结论．‎ ‎【解答】证明：∵∠ABD+∠3=180°∠ABC+∠4=180°，且∠3=∠4，‎ ‎∴∠ABD=∠ABC 在△ADB和△ACB中，‎ ‎，‎ ‎∴△ADB≌△ACB（ASA），‎ ‎∴BD=BC．‎ ‎　‎ 四、本大题共3小题，每小题10分，共30分 ‎20．（10分）先化简，再求值：（2m+1）（2m﹣1）﹣（m﹣1）2+（2m）3÷‎ ‎（﹣8m），其中m是方程x2+x﹣2=0的根 ‎【分析】先利用平方差公式和完全平方公式及单项式的除法化简原式，再由方程的解的定义得出m2+m=2，代入计算可得．‎ ‎【解答】解：原式=4m2﹣1﹣（m2﹣2m+1）+8m3÷（﹣8m）‎ ‎=4m2﹣1﹣m2+2m﹣1﹣m2‎ ‎=2m2+2m﹣2‎ ‎=2（m2+m﹣1），‎ ‎∵m是方程x2+x﹣2=0的根，‎ ‎∴m2+m﹣2=0，即m2+m=2，‎ 则原式=2×（2﹣1）=2．‎ ‎　‎ ‎21．（10分）某校八年级甲、乙两班各有学生50人，为了了解这两个班学生身体素质情况，进行了抽样调查，过程如下，请补充完整．‎ ‎（1）收集数据 从甲、乙两个班各随机抽取10名学生进行身体素质测试，测试成绩（百分制）如下：‎ 甲班65 75 75 80 60 50 75 90 85 65‎ 乙班90 55 80 70 55 70 95 80 65 70‎ ‎（2）整理描述数据 按如下分数段整理、描述这两组样本数据：‎ 成绩x 人数 班级 ‎50≤x＜60‎ ‎60≤x＜70‎ ‎70≤x＜80‎ ‎80≤x＜90‎ ‎90≤x≤100‎ 甲班 ‎1‎ ‎3‎ ‎3‎ ‎2‎ ‎1‎ 乙班 ‎2‎ ‎1‎ m ‎2‎ n 在表中：m=　3　，n=　2　．‎ ‎（3）分析数据 ‎①两组样本数据的平均数、中位数、众数如表所示：‎ 班级 平均数 中位数 众数 甲班 ‎72‎ x ‎75‎ 乙班 ‎72‎ ‎70‎ y 在表中：x=　75　，y=　70　．‎ ‎②若规定测试成绩在80分（含80分）以上的学生身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生有　20　人．‎ ‎③现从甲班指定的2名学生（1男1女），乙班指定的3名学生（2男1女）中分别抽取1名学生去参加上级部门组织的身体素质测试，用树状图和列表法求抽到的2名同学是1男1女的概率．‎ ‎【分析】（2）由收集的数据即可得；‎ ‎（3）①根据众数和中位数的定义求解可得；‎ ‎②用总人数乘以乙班样本中优秀人数所占比例可得；‎ ‎③列表得出所有等可能结果，利用概率公式求解可得．‎ ‎【解答】解：（2）由收集的数据得知m=3、n=2，‎ 故答案为：3、2；‎ ‎（3）①甲班成绩为：50、60、65、65、75、75、75、80、85、90，‎ ‎∴甲班成绩的中位数x==75，‎ 乙班成绩70分出现次数最多，所以的众数y=70，‎ 故答案为：75、70；‎ ‎②估计乙班50名学生中身体素质为优秀的学生有50×=20人；‎ ‎③列表如下：‎ 男 女 男 男、男 女、男 男 男、男 女、男 女 男、女 女、女 由表可知，共有6种等可能结果，其中抽到的2名同学是1男1女的有3种结果，‎ 所以抽到的2名同学是1男1女的概率为=．‎ ‎　‎ ‎22．（10分）某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜．如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y （℃）与时间x（h）之间的函数关系，其中线段AB、BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段．‎ 请根据图中信息解答下列问题：‎ ‎（1）求这天的温度y与时间x（0≤x≤24）的函数关系式；‎ ‎（2）求恒温系统设定的恒定温度；‎ ‎（3）若大棚内的温度低于10℃时，蔬菜会受到伤害．问这天内，恒温系统最多可以关闭多少小时，才能使蔬菜避免受到伤害？‎ ‎【分析】（1）应用待定系数法分段求函数解析式；‎ ‎（2）观察图象可得；‎ ‎（3）代入临界值y=10即可．‎ ‎【解答】解：（1）设线段AB解析式为y=k1x+b（k≠0）‎ ‎∵线段AB过点（0，10），（2，14）‎ 代入得 解得 ‎∴AB解析式为：y=2x+10（0≤x＜5）‎ ‎∵B在线段AB上当x=5时，y=20‎ ‎∴B坐标为（5，20）‎ ‎∴线段BC的解析式为：y=20（5≤x＜10）‎ 设双曲线CD解析式为：y=（k2≠0）‎ ‎∵C（10，20）‎ ‎∴k2=200‎ ‎∴双曲线CD解析式为：y=（10≤x≤24）‎ ‎∴y关于x的函数解析式为：‎ y=‎ ‎（2）由（1）恒温系统设定恒温为20°C ‎（3）把y=10代入y=中，解得，x=20‎ ‎∴20﹣10=10‎ 答：恒温系统最多关闭10小时，蔬菜才能避免受到伤害．‎ ‎　‎ 五、本大题共2小题，每小题10分，共20分 ‎23．（10分）已知关于x的一元二次方程mx2+（1﹣5m）x﹣5=0（m≠0）．‎ ‎（1）求证：无论m为任何非零实数，此方程总有两个实数根；‎ ‎（2）若抛物线y=mx2+（1﹣5m）x﹣5=0与x轴交于A（x1，0）、B（x2，0）两点，且|x1﹣x2|=6，求m的值；‎ ‎（3）若m＞0，点P（a，b）与Q（a+n，b）在（2）中的抛物线上（点P、Q不重合），求代数式4a2﹣n2+8n的值．‎ ‎【分析】（1）直接利用△=b2﹣4ac，进而利用偶次方的性质得出答案；‎ ‎（2）首先解方程，进而由|x1﹣x2|=6，求出答案；‎ ‎（3）利用（2）中所求得出m的值，进而利用二次函数对称轴得出答案．‎ ‎【解答】（1）证明：由题意可得：‎ ‎△=（1﹣5m）2﹣4m×（﹣5）‎ ‎=1+25m2﹣10m+20m ‎=25m2+10m+1‎ ‎=（5m+1）2≥0，‎ 故无论m为任何非零实数，此方程总有两个实数根；‎ ‎（2）解：mx2+（1﹣5m）x﹣5=0，‎ 解得：x1=﹣，x2=5，‎ 由|x1﹣x2|=6，‎ 得|﹣﹣5|=6，‎ 解得：m=1或m=﹣；‎ ‎（3）解：由（2）得，当m＞0时，m=1，‎ 此时抛物线为y=x2﹣4x﹣5，其对称轴为：x=2，‎ 由题已知，P，Q关于x=2对称，‎ ‎∴=2，即2a=4﹣n，‎ ‎∴4a2﹣n2+8n=（4﹣n）2﹣n2+8n=16．‎ ‎　‎ ‎24．（10分）如图，P是⊙O外的一点，PA、PB是⊙O的两条切线，A、B是切点，PO交AB于点F，延长BO交⊙O于点C，交PA的延长交于点Q，连结AC．‎ ‎（1）求证：AC∥PO；‎ ‎（2）设D为PB的中点，QD交AB于点E，若⊙O的半径为3，CQ=2，求的值．‎ ‎【分析】（1）根据切线长定理得出PA=PB，且PO平分∠BPA，利用等腰三角形三线合一的性质得出PO⊥AB．根据圆周角定理得出AC⊥AB，进而得到AC∥PO；‎ ‎（2）连结OA、DF．先用勾股定理计算出AQ=4，再计算出PA=PB=6，利用切线长定理可得到F点为AB的中点，易得DF为△BAP的中位线，则DF=PA=3，DF∥PA，利用DF∥AQ得到△DFE∽△QEA，所以==，设AE=4t，FE=3t，则AF=AE+FE=7t，于是BE=BF+FE=AF+FE=7t+3t=10t，最后计算．‎ ‎【解答】（1）证明：∵PA、PB是⊙O的两条切线，A、B是切点，‎ ‎∴PA=PB，且PO平分∠BPA，‎ ‎∴PO⊥AB．‎ ‎∵BC是直径，‎ ‎∴∠CAB=90°，‎ ‎∴AC⊥AB，‎ ‎∴AC∥PO；‎ ‎（2）解：连结OA、DF，如图，‎ ‎∵PA、PB是⊙O的两条切线，A、B是切点，‎ ‎∴∠OAQ=∠PBQ=90°．‎ 在Rt△OAQ中，OA=OC=3，∴OQ=5．‎ 由QA2+OA2=OQ2，得QA=4．‎ 在Rt△PBQ中，PA=PB，QB=OQ+OB=8，‎ 由QB2+PB2=PQ2，得82+PB2=（PB+4）2，‎ 解得PB=6，‎ ‎∴PA=PB=6，‎ ‎∵OP⊥AB，‎ ‎∴BF=AF=AB．‎ 又∵D为PB的中点，‎ ‎∴DF∥AP，DF=PA=3，‎ ‎∴△DFE∽△QEA，‎ ‎∴==，‎ 设AE=4t，FE=3t，则AF=AE+FE=7t，‎ ‎∴BE=BF+FE=AF+FE=7t+3t=10t，‎ ‎∴==．‎ ‎　‎ 六、本大题共2小题，第25题12分，第26题13分，共25分 ‎25．（12分）已知Rt△ABC中，∠ACB=90°，点D、E分别在BC、AC边上，连结BE、AD交于点P，设AC=kBD，CD=kAE，k为常数，试探究∠APE的度数：‎ ‎（1）如图1，若k=1，则∠APE的度数为　45°　；‎ ‎（2）如图2，若k=，试问（1）中的结论是否成立？若成立，请说明理由；若不成立，求出∠APE的度数．‎ ‎（3）如图3，若k=，且D、E分别在CB、CA的延长线上，（2）中的结论是否成立，请说明理由．‎ ‎【分析】（1）先判断出四边形ADBF是平行四边形，得出BD=AF，BF=AD，进而判断出△FAE≌△ACD，得出EF=AD=BF，再判断出∠EFB=90°，即可得出结论；‎ ‎（2）先判断出四边形ADBF是平行四边形，得出BD=AF，BF=AD，进而判断出△FAE∽△ACD，再判断出∠EFB=90°，即可得出结论；‎ ‎（3）先判断出四边形ADBF是平行四边形，得出BD=AF，BF=AD，进而判断出△ACD∽△HEA，再判断出∠EFB=90°，即可得出结论；‎ ‎【解答】解：（1）如图1，过点A作AF∥CB，过点B作BF∥AD相交于F，连接EF，‎ ‎∴∠FBE=∠APE，∠FAC=∠C=90°，‎ 四边形ADBF是平行四边形，‎ ‎∴BD=AF，BF=AD，‎ ‎∵AC=BD，CD=AE，‎ ‎∴AF=AC，‎ ‎∵∠FAC=∠C=90°，‎ ‎∴△FAE≌△ACD，‎ ‎∴EF=AD=BF，∠FEA=∠ADC，‎ ‎∵∠ADC+∠CAD=90°，‎ ‎∴∠FEA+∠CAD=90°=∠EHD，‎ ‎∵AD∥BF，‎ ‎∴∠EFB=90°，‎ ‎∵EF=BF，‎ ‎∴∠FBE=45°，‎ ‎∴∠APE=45°，‎ 故答案为：45°．‎ ‎（2）（1）中结论不成立，理由如下：‎ 如图2，‎ 过点A作AF∥CB，过点B作BF∥AD相交于F，连接EF，‎ ‎∴∠FBE=∠APE，∠FAC=∠C=90°，‎ 四边形ADBF是平行四边形，‎ ‎∴BD=AF，BF=AD，‎ ‎∵AC=BD，CD=AE，‎ ‎∴，‎ ‎∵BD=AF，‎ ‎∴，‎ ‎∵∠FAC=∠C=90°，‎ ‎∴△FAE∽△ACD，‎ ‎∴=，∠FEA=∠ADC，‎ ‎∵∠ADC+∠CAD=90°，‎ ‎∴∠FEA+∠CAD=90°=∠EMD，∵AD∥BF，‎ ‎∴∠EFB=90°，‎ 在Rt△EFB中，tan∠FBE=，‎ ‎∴∠FBE=30°，‎ ‎∴∠APE=30°，‎ ‎（3）（2）中结论成立，如图3，作EH∥CD，DH∥BE，EH，DH相交于H，连接AH，‎ ‎∴∠APE=∠ADH，∠HEC=∠C=90°，四边形EBDH是平行四边形，‎ ‎∴BE=DH，EH=BD，‎ ‎∵AC=BD，CD=AE，‎ ‎∴，‎ ‎∵∠HEA=∠C=90°，‎ ‎∴△ACD∽△HEA，‎ ‎∴，∠ADC=∠HAE，‎ ‎∵∠CAD+∠ADC=90°，‎ ‎∴∠HAE+∠CAD=90°，‎ ‎∴∠HAD=90°，‎ 在Rt△DAH中，tan∠ADH==，‎ ‎∴∠ADH=30°，‎ ‎∴∠APE=30°．‎ ‎　‎ ‎26．（13分）如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点，交y轴于点C（0，﹣），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=．‎ ‎（1）求抛物线的解析式；‎ ‎（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P运动到点A时，点Q也停止运动，设运动时间为t秒．‎ ‎①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．‎ ‎②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．‎ ‎【分析】（1）应用待定系数法求解析式 ‎（2）①分别用t表示△ADC、△PQA各边，应用分类讨论相似三角形比例式，求t值；‎ ‎②分别用t表示△APQ与△CAQ的面积之和，讨论最大值．‎ ‎【解答】解：（1）∵OA=1，OB=4‎ ‎∴A（1，0），B（﹣4，0）‎ 设抛物线的解析式为y=a（x+4）（x﹣1）‎ ‎∵点C（0，﹣）在抛物线上 ‎∴﹣‎ 解得a=‎ ‎∴抛物线的解析式为y=‎ ‎（2）存在t，使得△ADC与△PQA相似．‎ 理由：①在Rt△AOC中，OA=1，OC=‎ 则tan∠ACO=‎ ‎∵tan∠OAD=‎ ‎∴∠OAD=∠ACO ‎∵直线l的解析式为y=‎ ‎∴D（0，﹣）‎ ‎∵点C（0，﹣）‎ ‎∴CD=‎ 由AC2=OC2+OA2，得AC=‎ 在△AQP中，AP=AB﹣PB=5﹣2t，AQ=t 由∠PAQ=∠ACD，要使△ADC与△PQA相似 只需或 则有或 解得t1=，t2=‎ ‎∵t1＜2.5，t2＜2.5‎ ‎∴存在t=或t=，使得△ADC与△PQA相似 ‎②存在t，使得△APQ与△CAQ的面积之和最大 理由：作PF⊥AQ于点F，CN⊥AQ于N 在△APF中，PF=AP•sin∠PAF=‎ 在△AOD中，由AD2=OD2+OA2，得AD=‎ 在△ADC中，由S△ADC=‎ ‎∴CN=‎ ‎∴S△AQP+S△AQC=‎ ‎=﹣‎ ‎∴当t=时，△APQ与△CAQ的面积之和最大 ‎　‎