浙江中考数学专题训练——选择题3 13页

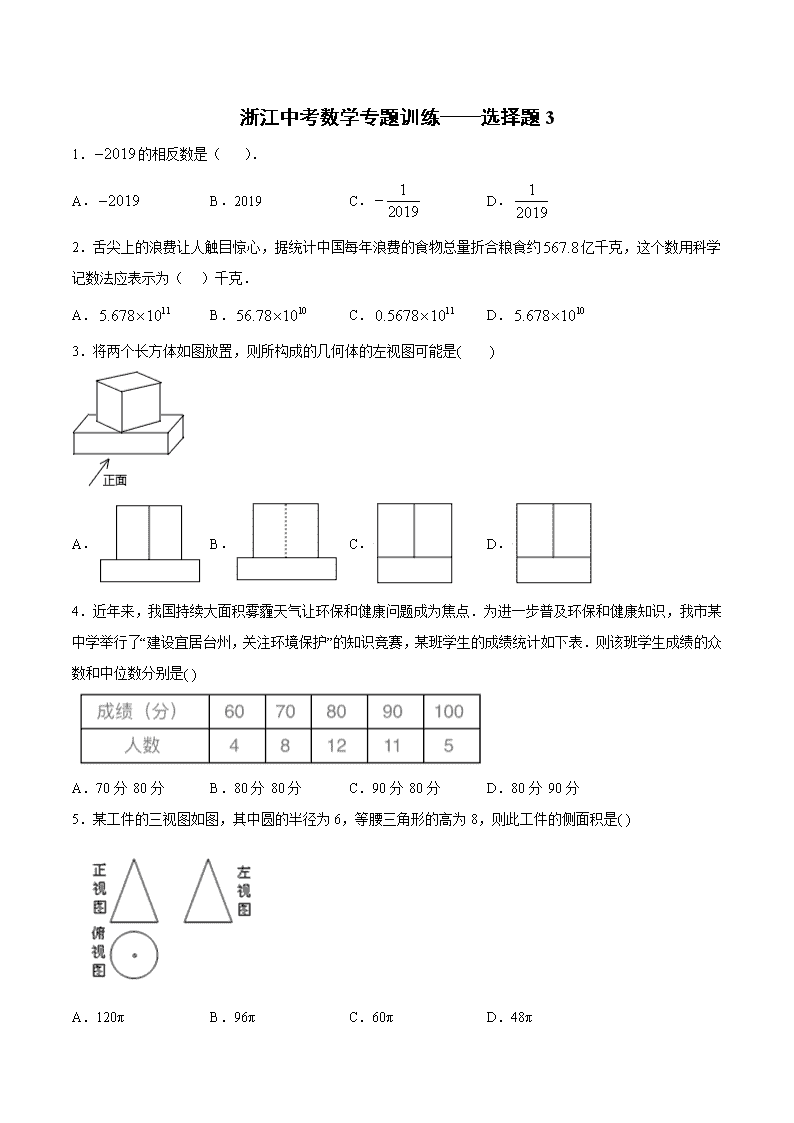
浙江中考数学专题训练——选择题3‎ ‎1．的相反数是（ ）．‎ A． B．2019 C． D．‎ ‎2．舌尖上的浪费让人触目惊心，据统计中国每年浪费的食物总量折合粮食约亿千克，这个数用科学记数法应表示为（ ）千克．‎ A． B． C． D．‎ ‎3．将两个长方体如图放置，则所构成的几何体的左视图可能是(　　)‎ A． B． C． D．‎ ‎4．近年来，我国持续大面积雾霾天气让环保和健康问题成为焦点．为进一步普及环保和健康知识，我市某中学举行了“建设宜居台州，关注环境保护”的知识竞赛，某班学生的成绩统计如下表．则该班学生成绩的众数和中位数分别是( )‎ A．70分 80分 B．80分 80分 C．90分 80分 D．80分 90分 ‎5．某工件的三视图如图，其中圆的半径为6，等腰三角形的高为8，则此工件的侧面积是( ) ‎ A．120π B．96π C．60π D．48π ‎6．2018年宁波的GDP达到了10746亿元人民币，用科学计数法表示10746亿为（ ）‎ A．1.0746×10-4 B．1.0746×104 C．1.0746×10-12 D．1.0746×1012‎ ‎7．温州某生态示范园计划种植一批桔树，原计划总产值为20万千克，为满足市场需求，现决定改良种植技术，改良后平均每亩产量是原来的1.5倍，总产量比原计划增加了4万千克，种植亩数减少了10亩，则原来平均每亩产量是多少万千克？设原来平均每亩产量为x万千克，根据题意列方程为（　　）‎ A． B．‎ C． D．‎ ‎8．如图，在中，，，、分别是的高线与中线，点是线段的中点，连接．若，则（ ）‎ A．10 B．11 C．12 D．13‎ ‎9．如图，∠AOB为锐角，在射线OA上依次截取A1A2＝A2A3＝A3A4＝…＝AnAn+1，在射线OB上依次截取B1B2＝B2B3＝B3B4＝…＝BnBn+1，记Sn为△AnBnBn+1的面积（n为正整数），若S3＝7，S4＝10，则S2019＝（　　）‎ A．4039 B．4041 C．6055 D．6058‎ ‎10．如图，圆内接四边形ABCD的边AB过圆心O，过点C的切线与边AD所在直线垂直于点M，若∠ABC=55°，则∠ACD等于（ ）‎ A．20° B．35° C．40° D．55°‎ ‎11．如图，中，，，，则的长为（ ）‎ A． B． C．5 D．‎ ‎12．对于实数，定义运算“*”；关于的方程恰好有三个不相等的实数根，则的取值范围是（ ）‎ A． B．‎ C． D．‎ ‎13．在平面直角坐标系中，先将抛物线y＝2x2﹣4x关于y轴作轴对称变换，再将所得的抛物线，绕它的顶点旋转180°，那么经两次变换后所得的新抛物线的函数表达式为（　　）‎ A．y＝﹣2x﹣4x B．y＝﹣2x+4x C．y＝﹣2x﹣4x﹣4 D．y＝﹣2x+4x+4‎ ‎14．如图，在4×4的网格中，每一个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点，以O为坐标原点建立如图所示的平面直角坐标系．若抛物线y＝x2+bx+c的图象至少经过图中（4×4的网格中）的三个格点，并且至少一个格点在x轴上，则符合要求的抛物线一定不经过的格点坐标为（　　）‎ A．（1，3） B．（2，3） C．（1，4） D．（2，4）‎ 二、填空题 ‎15．函数的图象向右平移2个单位后解析式变为 （ ）‎ A． B． C． D．‎ 参考答案 ‎1．B ‎【解析】‎ ‎【分析】‎ 根据相反数知识直接写出即可.‎ ‎【详解】‎ 解：的相反数是2019，‎ 故选B.‎ ‎【点睛】‎ 本题是对相反数的考查，熟练掌握相反数知识是解决本题的关键.‎ ‎2．D ‎【解析】‎ ‎【分析】‎ 先将亿改写为56780000000，再根据科学记数法的形式为，其中，n是原数的整数位数减1，即可得出答案．‎ ‎【详解】‎ 亿=56780000000=，‎ 故选D．‎ ‎【点睛】‎ 本题考查科学记数法，其形式为，其中，n是整数，关键是确定和n的值．‎ ‎3．C ‎【解析】‎ 根据原几何体的特征及放置位置，可以判断选项C符合左视图的特征，故选C．‎ ‎4．B ‎【解析】‎ ‎【分析】‎ 根据中位数的定义与众数的定义，结合图表信息解答．‎ ‎【详解】‎ 由题中的数据可知，80出现的次数最多，所以众数为80(分)；‎ 这组数据的个数是，中间的第20和第21个数都是80，则中位数是80(分)；‎ 故选：B．‎ ‎【点睛】‎ 本题考查了众数和中位数，掌握众数和中位数的概念是解题的关键，众数是一组数据中出现次数最多的数，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）．‎ ‎5．C ‎【解析】‎ ‎【分析】‎ 根据三视图可知，此工件为圆锥，求出圆锥的母线长及圆锥的底面圆周长即可求出圆锥的侧面积．‎ ‎【详解】‎ 如图：∵AO=8，CO=6，‎ ‎ ∴,‎ ‎⊙O周长为，‎ ‎∴此工件侧面积为 故选：C．‎ ‎【点睛】‎ 本题考查了圆锥的计算和由三视图判断几何体，根据三视图判断出几何体的形状是解题的关键一步，另外要熟悉扇形的侧面展开图及扇形的面积公式．‎ ‎6．D ‎【解析】‎ ‎【分析】‎ 用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，据此判断即可．‎ ‎【详解】‎ ‎10746亿=10746×108=1.0746×1012‎ 故选：D ‎【点睛】‎ 此题主要考查了用科学记数法表示较大的数，一般形式为a×10n，其中1≤|a|＜10，确定a与n的值是解题的关键．‎ ‎7．B ‎【解析】‎ ‎【分析】‎ 根据题意可得等量关系：原计划种植的亩数﹣改良后种植的亩数＝10亩，根据等量关系列出方程即可．‎ ‎【详解】‎ 解：设原来平均每亩产量为x万千克，则改良后平均每亩产量为1.5x万千克，‎ 根据题意列方程为： ‎ 故选：B．‎ ‎【点睛】‎ 本题考查了分式方程的实际应用，找到合适的等量关系是解题的关键．‎ ‎8．A ‎【解析】‎ ‎【分析】‎ 连接DE，根据直角三角形的性质得到AB=2DE，根据线段垂直平分线的性质得到DE=DC，得到AB=2CD，根据勾股定理列式计算得到得到答案．‎ ‎【详解】‎ 解：连接DE，∵AD⊥BC，点E是AB的中点，‎ ‎ ∴AB=2DE， ∵DF⊥CE，点F是线段CE的中点，‎ ‎ ∴DE=DC， ∴AB=2CD， ‎ 在Rt△ABD中，， ‎ 在Rt△ACD中，，‎ ‎ ∴，‎ 即，‎ ‎ 解得，CD=5， ∴AB=2CD=10，‎ ‎ 故选：A．‎ ‎【点睛】‎ 本题考查的是勾股定理、直角三角形的性质，熟练掌握定理是关键．‎ ‎9．C ‎【解析】‎ ‎【分析】‎ 过A3作A3C⊥OB于C，过A4作A4D⊥OB于D，过A2019作A2019E⊥OB于E，则△OA3C∽△OA4D∽△OA2019E，设OA1＝a，A1A2＝A2A3＝A3A4＝…＝AnAn+1＝1个单位，由等底的三角形面积比等于三角形的高之比，得出，即，可得a＝，由相似三角形的性质得出，即可求出S2019＝6055．‎ ‎【详解】‎ 解：过A3作A3C⊥OB于C，过A4作A4D⊥OB于D，过A2019作A2019E⊥OB于E，‎ 则△OA3C∽△OA4D∽△OA2019E，‎ 设OA1＝a，A1A2＝A2A3＝A3A4＝…＝AnAn+1＝1个单位，‎ ‎∵S3＝7，S4＝10，B1B2＝B2B3＝B3B4＝…＝BnBn+1，‎ ‎∴，‎ 即，‎ 解得：a＝，‎ ‎∴，‎ ‎∴，‎ ‎∴S2019＝6055，‎ 故选：C．‎ ‎【点睛】‎ 本题考查了图形类的规律题问题，掌握相似三角形的性质以及判定定理是解题的关键．‎ ‎10．A ‎【解析】‎ 试题解析：∵圆内接四边形ABCD的边AB过圆心O，∴∠ADC+∠ABC=180°，∠ACB=90°，∴∠ADC=180°﹣∠ABC=125°，∠BAC=90°﹣∠ABC=35°，∵过点C的切线与边AD所在直线垂直于点M，∴∠MCA=∠ABC=55°，∠AMC=90°，∵∠ADC=∠AMC+∠DCM，∴∠DCM=∠ADC﹣∠AMC=35°，∴∠ACD=∠MCA﹣∠DCM=55°﹣35°=20°．故选A．‎ ‎11．C ‎【解析】‎ ‎【分析】‎ 过C作CD⊥AB于D，根据含30度角的直角三角形求出CD，解直角三角形求出AD，在△BDC 中解直角三角形求出BD，相加即可求出答案．‎ ‎【详解】‎ 过C作CD⊥AB于D，‎ 则∠ADC=∠BDC=90，‎ ‎∵∠A=30,AC=，‎ ‎∴CD=AC=,由勾股定理得：AD=CD=3，‎ ‎∵tanB==，‎ ‎∴BD=2，‎ ‎∴AB=2+3=5，‎ 故选C.‎ ‎【点睛】‎ 本题考查解直角三角形.‎ ‎12．C ‎【解析】‎ ‎【分析】‎ 设，根据定义得到函数解析式，由方程的有三个不同的解去掉函数图象与直线y=t的交点有三个，即可确定t的取值范围.‎ ‎【详解】‎ 设，由定义得到 ‎，‎ ‎∵方程恰好有三个不相等的实数根，‎ ‎∴函数的图象与直线y=t有三个不同的交点，‎ ‎∵的最大值是 ‎∴若方程恰好有三个不相等的实数根，则t的取值范围是，‎ 故选：C.‎ ‎【点睛】‎ 此题考查新定义的公式，抛物线与直线的交点与方程的解的关系，正确理解抛物线与直线的交点与方程的解的关系是解题的关键.‎ ‎13．C ‎【解析】‎ ‎【分析】‎ 若抛物线关于y轴作轴对称变换，则图象上所有的点纵坐标不变横坐标互为相反数；将其绕顶点旋转180°后，开口大小和顶点坐标都没有变化，变化的只是开口方向，可据此得出所求的结论．‎ ‎【详解】‎ 解：抛物线y＝2x2﹣4x关于y轴作轴对称变换，‎ 所得抛物线为y＝2（﹣x）2﹣4（﹣x）＝2x2+4x；‎ ‎∵y＝2x2+4x＝2（x+1）2﹣2，‎ ‎∴绕顶点旋转180°后，得：y＝﹣2（x+1）2﹣2＝﹣2x2﹣4x﹣4，‎ 故选：C．‎ ‎【点睛】‎ 此题考查了二次函数图象的几何变换，在绕抛物线顶点旋转过程中，二次函数的开口大小和顶点坐标都没有变化．‎ ‎14．B ‎【解析】‎ ‎【分析】‎ 二次项系数为1，该抛物线开口向上，根据二次函数的图象和性质进行分析：若过（1，3），则可过点（2，0），此时抛物线解析式为：y＝x2-6x+8，过另一个点（4，0），故A不符合题意；同理，可计算B，C，D选项中的格点是否符合题意.‎ ‎【详解】‎ 解：∵二次项系数为1，‎ ‎∴该抛物线开口向上 选项A：若过（1，3），则可过点（2，0），此时抛物线解析式为：y＝x2-6x+8，过另一个点（4，0），故A不符合题意；‎ 选项B：若过（2，3），则可过点（3，1），此时抛物线解析式为：y＝x2﹣7x+13，若同时过x轴上的可能的格点（4，0），此时x＝4时，y＝1，故B符合题意；‎ 选项C：若过（1，4），则可过点（3，0），此时抛物线解析式为：y＝x2-6x+9，过另一个点（4，1），故C不符合题意；‎ 选项D：若过（2，4），则可过点（4，0），此时抛物线解析式为：y＝x2-8x+16，过另一个点（3，1），故D不符合题意；‎ 故选：B．‎ ‎【点睛】‎ 本题考查的是二次函数的图象和性质，难点在于根据函数的解析式去分析可过哪些点，由于题目计算量大，本题可采取排除法求解．‎ ‎15．C ‎【解析】‎ 根据二次函数图象平移规律:上加下减,左加右减,因此二次函数的图象向右平移2个 单位后解析式是,故选C.‎