人教版九年级上册数学同步练习课件-第22章 二次函数-22二次函数与一元二次方程(一课时) 16页

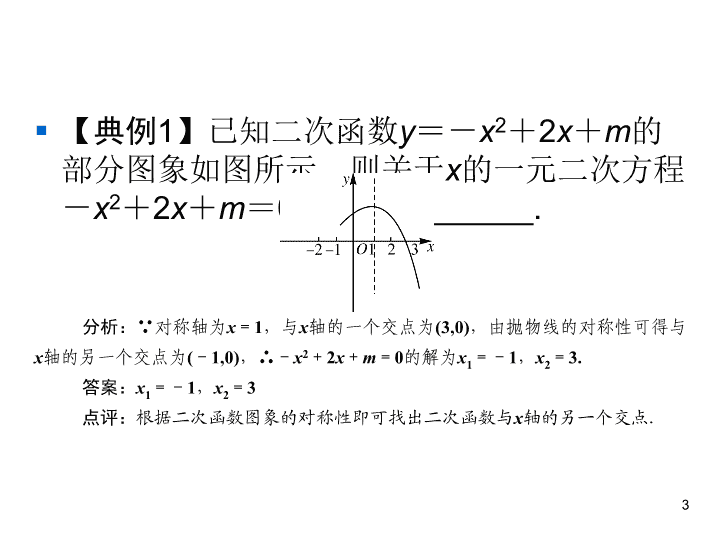
第二十二章　二次函数 22.2　二次函数与一元二次方程(一课时) § 知识点1　二次函数与一元二次方程 § (1)如果抛物线y＝ax2＋bx＋c与x轴有公共点， 那么公共点的横坐标就是方程ax2＋bx＋c＝0 的根． § (2)抛物线y＝ax2＋bx＋c与x轴的位置关系有 三种：没有公共点、有一个公共点、有两个 公共点，它们分别对应着一元二次方程ax2＋ bx＋c＝0的实数根的三种情况：没有实数根、 有两个相等的实数根、有两个不相等的实数 根． 2 § 【典例1】已知二次函数y＝－x2＋2x＋m的 部分图象如图所示，则关于x的一元二次方程 －x2＋2x＋m＝0的解为________. 3 分析：∵对称轴为x＝1，与x轴的一个交点为(3,0)，由抛物线的对称性可得与 x轴的另一个交点为(－1,0)，∴－x2＋2x＋m＝0的解为x1＝－1，x2＝3. 答案：x1＝－1，x2＝3 点评：根据二次函数图象的对称性即可找出二次函数与x轴的另一个交点． 4 § 分析：ax2＋bx＋c＝0的解就是函数y＝ax2＋ bx＋c的函数值为0时自变量x的值．从表中 可知，当6.18＜x＜6.19时，－0.01＜y＜ 0.02，即这个范围内必有一个x使y＝0. § 答案：C 5 6 C　 C　 § 3．如图，二次函数y＝ax2＋bx＋c的图象与x 轴相交于(－2,0)和(4,0)两点，当函数值y＞0 时，自变量x的取值范围是 (　　) § A．x＜－2　 § B．－2＜x＜4　 § C．x＞0　 § D．x＞4 7 B　 § 4．如图，以(1，－4)为顶点的二次函数y＝ ax2＋bx＋c的图象与x轴交于点A，则一元二 次方程ax2＋bx＋c＝0的正数解的范围是 (　　) § A．2＜x＜3　 § B．3＜x＜4　 § C．4＜x＜5　 § D．5＜x＜6 8 C　 § 5．对于二次函数y＝x2－2mx－3，下列结论 错误的是 (　　) § A．它的图象与x轴有两个交点 § B．方程x2－2mx＝3的两根之积为－3 § C．它的图象的对称轴在y轴的右侧 § D．x＜m时，y随x的增大而减小 9 C　 10 C　 11 D　 § 8．【2018·四川自贡中考】若函数y＝x2＋ 2x－m的图象与x轴有且只有一个交点，则m 的值为_______. § 9．已知抛物线y＝ax2＋bx＋c(a≠0)与x轴交 于A、B两点，若点A的坐标为(－2,0)，抛物 线的对称轴为x＝2，则线段AB的长为_____. § 10．如图，二次函数y＝ax2＋bx＋3的图象 经过点A(－1,0)、B(3,0)，那么一元二次方程 ax2＋bx＝0的根是________________. 12 －1　 8　 x1＝0，x2＝2　 § 11．利用函数的图象，求方程x2＋ 2x－3＝0的解． § 解：图象略．方程x2＋2x－3＝0的 解为x1＝－3，x2＝1. § 12．二次函数y＝ax2＋bx的图象如 图，若一元二次方程ax2＋bx＋m ＝0有实数根，求m的最大值． 13 § 13．如图，抛物线y＝ax2＋2ax＋1与x轴仅 有一个公共点A，经过点A的直线交该抛物线 于点B，交y轴于点C，且点C是线段AB的中 点． § (1)求这条抛物线的函数解析式； § (2)求直线AB的函数解析式． § 解：(1)抛物线的解析式为y＝x2＋2x＋1. § (2)直线AB的解析式为y＝2x＋2. 14 § 14．画出函数y＝x2－2x－3的图象，根据图 象回答下列问题． § (1)求图象与x轴、y轴的交点坐标； § (2)当x取何值时，y＝0？这里x的取值与方程 x2－2x－3＝0有什么关系？ § (3)x的取值在什么范围时，函数值y大于0？x 的取值在什么范围时，函数值y小于0? 15 § 解：图象如图所示：(1)图象与x轴的交点坐 标为(－1,0)，(3,0)，与y轴的交点坐标为(0， －3)．　(2)当x＝－1或x＝3时，y＝0.x的取 值与方程x2－2x－3＝0的解相同．　(3)当x ＜－1或x＞3时，y＞0；当 －1＜x＜3时，y ＜0. 16