2013年四川省达州市中考数学试卷及答案(解析版) 13页

达州市2013年高中阶段教育学校招生统一考试 数 学 本试卷分为第I卷（选择题）和第II卷（非选择题）两部分。第I卷1至2页，第II卷3至10页。考试时间120分钟，满分120分。‎ 第I卷（选择题，共30分）‎ 温馨提示：‎ ‎1、答第I卷前，请考生务必将姓名、准考证号、考试科目等按要求填涂在机读卡上。‎ ‎2、每小题选出正确答案后，请用2B铅笔把机读卡上对应题号的答案标号涂黑。‎ ‎3、考试结束后，请将本试卷和机读卡一并交回。‎ 一．选择题：（本题10个小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．－2013的绝对值是（ ）‎ A．2013 B．‎-2013 C．±2013 D．‎ 答案：A 解析：负数的绝对值是它的相反数，故选A。‎ ‎2．某中学在芦山地震捐款活动中，共捐款二十一万三千元。这一数据用科学记数法表示为（ ）‎ A．元 B．元 C．元 D．元 答案：C 解析：科学记数法写成：形式，其中，二十一万三千元＝213000＝元 ‎3．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）‎ 答案：D 解析：A、C只是轴对称图形，不是中心对称图形；B是中心对称图形，不是轴对称轴图形，只有D符合。‎ ‎4．甲、乙、丙三家超市为了促销一种定价相同的商品，甲超市先降价20%，后又降价10%；乙超市连续两次降价15%；丙超市一次降价30%。那么顾客到哪家超市购买这种商品更合算（　）‎ A．甲 B．乙 C．丙 D．一样 答案：C 解析：设原价a元，则降价后，甲为：a（1－20%）（1－10%）＝0.72a元，‎ 乙为：（1－15%）2a＝0.7225a元，丙为：（1－30%）a＝0.7a元，所以，丙最便宜。‎ ‎5．下面是一天中四个不同时刻两座建筑物的影子，将它们按时间先后顺序正确的是（　）‎ A．（3）（1）（4）（2） B．（3）（2）（1）（4） ‎ C．（3）（4）（1）（2） D．（2）（4）（1）（3）‎ 答案：C 解析：因为太阳从东边出来，右边是东，所以，早上的投影在左边，（3）最先，下午的投影在右边，（2）最后，选C。‎ ‎6．若方程有两个不相等的实数根，则m的取值范围在数轴上表示正确的是（　）‎ 答案：B 解析：因为方程有两个不相等的实数根，所以，△＝36－12m＞0，得m＜3，故选B。‎ ‎7．下列说法正确的是（　 ）‎ A．一个游戏中奖的概率是，则做100次这样的游戏一定会中奖 B．为了了解全国中学生的心理健康状况，应采用普查的方式 C．一组数据0，1，2，1，1的众数和中位数都是1‎ D．若甲组数据的方差，乙组数据的方差，则乙组数据比甲组数据稳定 答案：C 解析：由概率的意义，知A错；全国中学生较多，应采用抽样调查，故B也错；经验证C正确；方差小的稳定，在D中，应该是甲较稳定，故D错。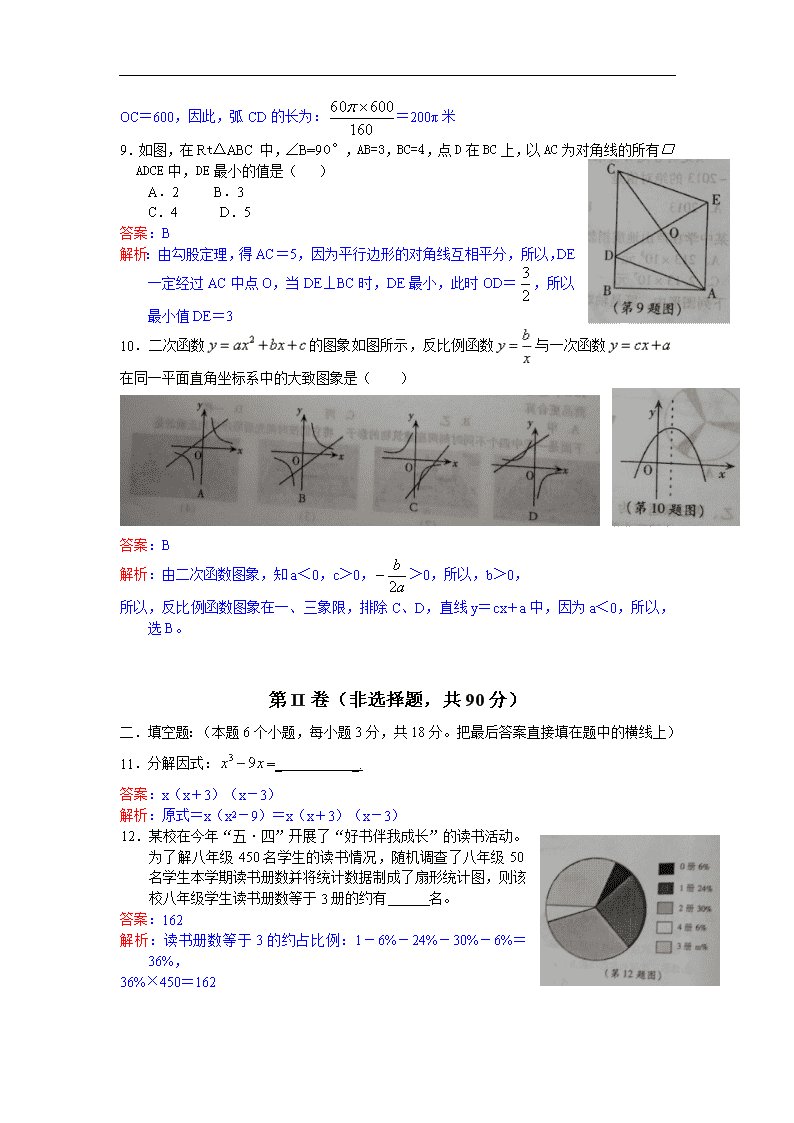‎ ‎8．如图，一条公路的转变处是一段圆弧（即图中弧CD，点O是弧CD的圆心），其中CD=‎600米，E为弧CD上一点，且OE⊥CD，垂足为F，OF=米，则这段弯路的长度为（　）‎ A．200π米 B．100π米 C．400π米 D．300π米 答案：A 解析：CF＝300，OF＝，所以，∠COF＝30°，∠COD＝60°，‎ OC＝600，因此，弧CD的长为：＝200π米 ‎9．如图，在Rt△ABC中，∠B=90°，AB=3，BC=4，点D在BC上，以AC为对角线的所有□ADCE中，DE最小的值是（　 ）‎ A．2 B．3‎ C．4 D．5‎ 答案：B 解析：由勾股定理，得AC＝5，因为平行边形的对角线互相平分，所以，DE一定经过AC中点O，当DE⊥BC时，DE最小，此时OD＝，所以最小值DE＝3‎ ‎10．二次函数的图象如图所示，反比例函数与一次函数在同一平面直角坐标系中的大致图象是（ 　 ）‎ 答案：B 解析：由二次函数图象，知a＜0，c＞0，＞0，所以，b＞0，‎ 所以，反比例函数图象在一、三象限，排除C、D，直线y＝cx＋a中，因为a＜0，所以，选B。‎ 第II卷（非选择题，共90分）‎ 二．填空题：（本题6个小题，每小题3分，共18分。把最后答案直接填在题中的横线上）‎ ‎11．分解因式：=_　　　　　_.‎ 答案：x（x＋3）（x－3）‎ 解析：原式＝x（x2－9）＝x（x＋3）（x－3）‎ ‎12．某校在今年“五·四”开展了“好书伴我成长”的读书活动。为了解八年级450名学生的读书情况，随机调查了八年级50名学生本学期读书册数，并将统计数据制成了扇形统计图，则该校八年级学生读书册数等于3册的约有　　　名。‎ 答案：162‎ 解析：读书册数等于3的约占比例：1－6%－24%－30%－6%＝36%，‎ ‎36%×450＝162‎ ‎13．点、在反比例函数的图象上，当时，,则k的取值可以是___　_（只填一个符合条件的k的值）.‎ 答案：－1‎ 解析：由题知，y随x的增大而增大，故k是负数，此题答案不唯一。‎ ‎14．如果实数x满足，那么代数式的值为_　　_.‎ 答案：5‎ 解析：由知，得＝3，原式＝＝5。‎ ‎15．如图，折叠矩形纸片ABCD，使B点落在AD上一点E处，折痕的两端点分别在AB、BC上（含端点），且AB=6，BC=10。设AE=x，则x 的取值范围是　　　　.‎ 答案：2≤x≤6‎ 解析：如图，设AG＝y，则BG＝6－y，在Rt△GAE中，‎ x2＋y2＝（6－y）2，即（，当y＝0时，x取最大值为6；当y＝时,x取最小值2，故有2≤x≤6‎ ‎16．如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2012BC和∠A2012CD的平分线交于点A2013，则∠A2013=　　　　度。‎ ‎ ‎ 答案：‎ 解析：∵A1B、A1C分别平分∠ABC和∠ACD， ∴∠ACD=k∠A1CD，∠ABC=2∠A1BC， 而∠A1CD=∠A1+∠A1BC，∠ACD=∠ABC+∠A， ‎ ‎∴∠A=2∠A1，∴∠A1=， 同理可得∠A1=2∠A2，即∠A=22∠A2，∴∠A2=，‎ 所以，猜想：∠A2013=‎ 三．解答题（72分，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎（一）（本题2个小题，共13分）‎ ‎17．（6分）计算：‎ 解析：原式＝1＋2－＋9＝10＋‎ ‎18．（7分）钓鱼岛自古以来就是中国领土。中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测。如图，E、F为钓鱼岛东西两端。某日，中国一艘海监船从A点向正北方向巡航，其航线距离钓鱼岛最近距离CF=公里，在A点测得钓鱼岛最西端F在最东端E的东北方向（C、F、E在同一直线上）。求钓鱼岛东西两端的距离。（，，结果精确到0.1）‎ 解析：‎ 由题知，在Rt△ACF中，∠ACF=90°,‎ ‎∠A=30°，CF=20公里.‎ ‎∴cot30°=.‎ 解得，AC=60（公里）.………………………(2分)‎ 又∵E在B的东北方向，且∠ACF=90°‎ ‎∴∠E=∠CBE=45°，‎ ‎∴CE=CB.………………………………………………(4分)‎ 又∵CB=AC-AB=60-22=38(公里)，‎ ‎∴CE=38公里.………………………(5分)‎ ‎∴EF=CE-CF=38-20≈3.4（公里）………………………(6分)‎ 答：钓鱼岛东西两端的距离约为3.4公里.………………………(7分)‎ ‎（二）（本题2个小题，共14分）‎ ‎19．（7分）已知，则 ‎……‎ 已知，求n的值。‎ 解析：由题知 f(1)+f(2)+f(3)+…+f(n)‎ ‎=+++…+‎ ‎=1-+-+-+…+-‎ ‎=1-………………………(4分）‎ ‎=.………………………(4分）‎ 又∵f(1)+f(2)+f(3)+…+f(n)=,‎ ‎∴=.‎ 解得n=14.………………………(6分）‎ 经检验，n=14是上述方程的解.‎ 故n的值为14.………………………(7分）‎ ‎20．（7分）某中学举行“中国梦·我的梦”演讲比赛。志远班的班长和学习委员都想去，于是老师制作了四张标有算式的卡片，背面朝上洗匀后，先由班长抽一张，再由学习委员在余下三张中抽一张。如果两张卡片上的算式都正确，班长去；如果两张卡片上的算式都错误，学习委员去；如果两张卡片上的算式一个正确一处错误，则都放回去，背面朝上洗匀后再抽。‎ 这个游戏公平吗？请用树状图或列表的方法，结合概率予以说明。‎ 解析：公平.………………………(1分)‎ 用列表法或树状图列出该事件的等可能情况如下：‎ 由此可知该事件共有12种等可能结果.………………………(4分)‎ ‎∵四张卡片中，A、B中的算式错误，C、D中的算式正确，‎ ‎∴都正确的有CD、DC两种，都错误的有AB、BA两种.………………………(5分)‎ ‎∴班长去的概率P（班长去）==，‎ 学习委员去的概率P（学习委员去）==，‎ P（班长去）=P（学习委员去)‎ ‎∴这个游戏公平.………………………(7分)‎ ‎（三）（本题2个小题，共16分）‎ ‎21．（8分）已知反比例函数的图象与一次函数的图象交于A、B两点，连结AO。‎ ‎（1）求反比例函数和一次函数的表达式；‎ ‎（2）设点C在y轴上，且与点A、O构成等腰三角形，请直接写出点C的坐标。‎ 解析：‎ ‎(1)∵y=的图像过点（，-3），‎ ‎∴k1=3xy=3××(-3)=-3.‎ ‎∴反比例函数为y.………………………(1分）‎ ‎∴a==1，‎ ‎∴A（-1,1）.………………………(2分）‎ ‎∴‎ 解得 ‎∴一次函数为y=-3x-2.………………………(4分）‎ 16、 C(0,)、………………………(5分）‎ 或（0，-）、………………………(6分）‎ 或（0,1）、………………………(7分）‎ 或（0，2）.………………………(8分）‎ ‎22．（8分）选取二次三项式中的两项，配成完全平方式的过程叫配方。例如 ①选取二次项和一次项配方：； ②选取二次项和常数项配方：， 或 ③选取一次项和常数项配方： 根据上述材料，解决下面问题： （1）写出的两种不同形式的配方；‎ ‎（2）已知，求的值。‎ 解析：：（1）＝x2-8x+16-16+4=(x-4)2-12‎ 或＝（x-2）2-4x ‎(2) ‎ X=-1,y=2.因此xy=(-1)2=1‎ ‎（四）（本题2个小题，共17分）‎ ‎23．（8分）今年，‎6月12日为端午节。在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况。请根据小丽提供的信息，解答小华和小明提出的问题。‎ ‎（1）小华的问题解答：‎ 解析：（1）解：设实现每天800元利润的定价为x元/个，根据题意，得 ‎（x-2)（500-×10）=800 .………………………(2分）‎ 整理得：x2-10x+24=0.‎ 解之得：x1=4,x2=6.………………………(3分）‎ ‎∵物价局规定，售价不能超过进价的240%，即2×240%=4.8（元）.‎ ‎∴x2=6不合题意,舍去,得x=4.‎ 答：应定价4元/个，才可获得800元的利润.………………………(4分）‎ ‎（2）解：设每天利润为W元，定价为x元/个，得 W=（x-2)(500-×10)‎ ‎=-100x2+1000x-1600‎ ‎=-100(x-5)2+900.………………………(6分）‎ ‎∵x≤5时W随x的增大而增大,且x≤4.8，‎ ‎∴当x=4.8 时，W最大，‎ W最大=-100×（4.8-5)2+900=896＞800 .………………………(7分）‎ 故800元不是最大利润.当定价为4.8元/个时，每天利润最大.………………………(8分）‎ ‎24．（9分）通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的。下面是一个案例，请补充完整。‎ FF 原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由。‎ ‎（1）思路梳理 ∵AB=CD， ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合。 ∵∠ADC=∠B=90°， ∴∠FDG=180°，点F、D、G共线。 根据__SAS__________，易证△AFG≌_△AFE_______，得EF=BE+DF。‎ ‎（2）类比引申 如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°。若∠B、∠D都不是直角，则当∠B与∠D满足等量关系_互补___时，仍有EF=BE+DF。‎ ‎（3）联想拓展 如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°。猜想BD、DE、EC应满足的等量关系，并写出推理过程。‎ ‎ 解：BD2+EC2=DE2‎ 解析：(1)SAS………………………(1分）‎ ‎ △AFE………………………(2分）‎ ‎(2)∠B+∠D=180°………………………(4分）‎ ‎(3)解：BD2+EC2=DE2.………………………(5分）‎ ‎∵AB=AC，‎ ‎∴把△ABD绕A点逆时针旋转90°至△ACG，可使AB与AC重合.‎ ‎∵△ABC中，∠BAC=90°.‎ ‎∴∠ACB+∠ACG=∠ACB+∠B=90°,即∠ECG=90°.‎ ‎∴EC2+CG2=EG2.………………………(7分）‎ 在△AEG与△AED中,‎ ‎∠EAG=∠EAC+∠CAG=∠EAC+∠BAD=90°-∠EAD=45°=∠EAD,‎ 又∵AD=AG，AE=AE，‎ ‎∴△AEG≌△AED.‎ ‎∴DE=EG.又∵CG=BD,‎ ‎∴BD2+EC2=DE2.………………………(9分）‎ ‎（五）（本题12分）‎ ‎25．如图，在直角体系中，直线AB交x轴于点A（5，0），交y轴于点B，AO是⊙M的直径，其半圆交AB于点C，且AC=3。取BO的中点D，连接CD、MD和OC。 （1）求证：CD是⊙M的切线；‎ ‎（2）二次函数的图象经过点D、M、A，其对称轴上有一动点P，连接PD、PM，求△PDM的周长最小时点P的坐标；‎ ‎（3）在（2）的条件下，当△PDM的周长最小时，抛物线上是否存在点Q，使？若存在，求出点Q的坐标；若不存在，请说明理由。‎ 解析：（1）证明：连结CM.‎ ‎∵OA 为⊙M直径,‎ ‎∴∠OCA=90°.‎ ‎∴∠OCB=90°.‎ ‎∵D为OB中点,‎ ‎∴DC=DO.‎ ‎∴∠DCO=∠DOC.………………………(1分）‎ ‎∵MO=MC,‎ ‎∴∠MCO=∠MOC.………………………(2分）‎ ‎∴∠DCM=∠DCO+∠MCO=∠DOC+∠MOC=∠DOM=90°.………………………(3分）‎ 又∵点C在⊙M上，‎ ‎ ∴DC是⊙M的切线.………………………(4分）‎ ‎（2）解：在Rt△ACO中,有OC=.‎ 又∵A点坐标（5，0）, AC=3,‎ ‎∴OC==4.‎ ‎∴tan∠OAC=.‎ ‎∴.解得 OB=.‎ 又∵D为OB中点，∴OD=. ‎ D点坐标为（0，).………………………(5分）‎ 连接AD，设直线AD的解析式为y=kx+b,则有 j解得 ‎∴直线AD为y=-x+.‎ ‎∵二次函数的图象过M（,0)、A(5,0)，‎ ‎∴抛物线对称轴x=.………………………(6分）‎ ‎∵点M、A关于直线x=对称，设直线AD与直线x=交于点P,‎ ‎∴PD+PM为最小.‎ 又∵DM为定长，‎ ‎∴满足条件的点P为直线AD与直线x=的交点.………………………(7分）‎ 当x=时,y=-+=.‎ 故P点的坐标为（，）.………………………(8分）‎ ‎（3）解：存在.‎ ‎∵S△PDM=S△DAM-S△PAM ‎=AM·yD-AM·yP ‎=AM(yD-yp).‎ S△QAM=AM·,由（2）知D（0，),P(，）,‎ ‎∴×（-）=yQ 解得yQ=±………………………(9分）‎ ‎∵二次函数的图像过M(0，)、A(5，0），‎ ‎∴设二次函数解析式为y=a(x-)（x-5).‎ 又∵该图象过点D（0，)，‎ a×(-）×(-5)=，a=.‎ ‎∴y=(x-)(x-5).………………………(10分）‎ 又∵C点在抛物线上，且yQ=±，‎ ‎∴(x-)(x-5)=±.‎ 解之，得x1=，x2=，x3=.‎ ‎∴点Q的坐标为（，)，或（，)，或（，-）.…………(12分）‎