2012年辽宁省锦州市中考数学试题（含答案） 14页

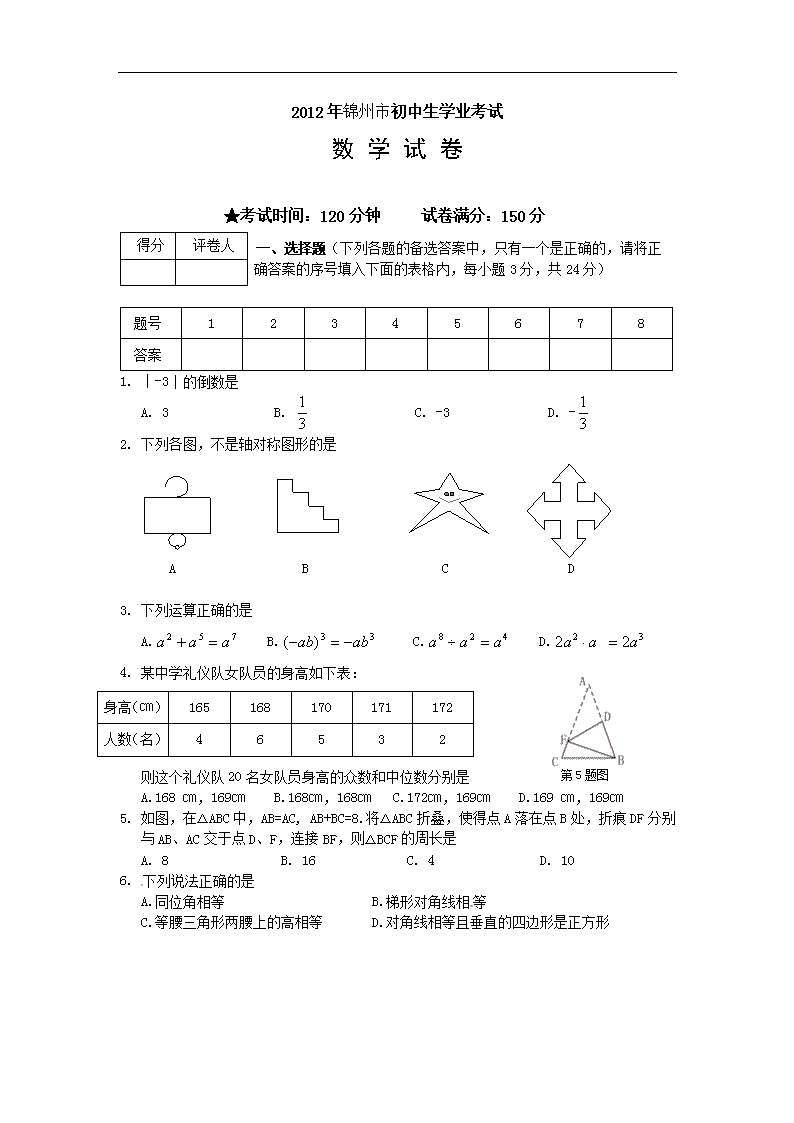
‎2012年锦州市初中生学业考试 数 学 试 卷 ‎★考试时间：120分钟 试卷满分：150分 得分 评卷人 一、选择题（下列各题的备选答案中，只有一个是正确的，请将正确答案的序号填入下面的表格内，每小题3分，共24分）[来源:学科网][来源:学.科.网][来源:学科网]‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 ‎1. ∣-3∣的倒数是 A. 3 B. C. -3 D. -‎ ‎2. 下列各图，不是轴对称图形的是 A B C D ‎3. 下列运算正确的是 A. B. C. D.‎ 第5题图 ‎4. 某中学礼仪队女队员的身高如下表：‎ 身高（㎝）‎ ‎165‎ ‎168‎ ‎170‎ ‎171‎ ‎172‎ 人数（名）‎ ‎4‎ ‎6‎ ‎5‎ ‎3‎ ‎2‎ ‎ 则这个礼仪队20名女队员身高的众数和中位数分别是 A.168 ㎝，169㎝ B.168㎝，168㎝ C.172㎝，169㎝ D.169 ㎝，169㎝ ‎5. 如图，在△ABC中，AB=AC, AB+BC=8.将△ABC折叠，使得点A落在点B处，折痕DF分别与AB、AC交于点D、F，连接BF，则△BCF的周长是 A. 8 B. 16 C. 4 D. 10‎ ‎6. 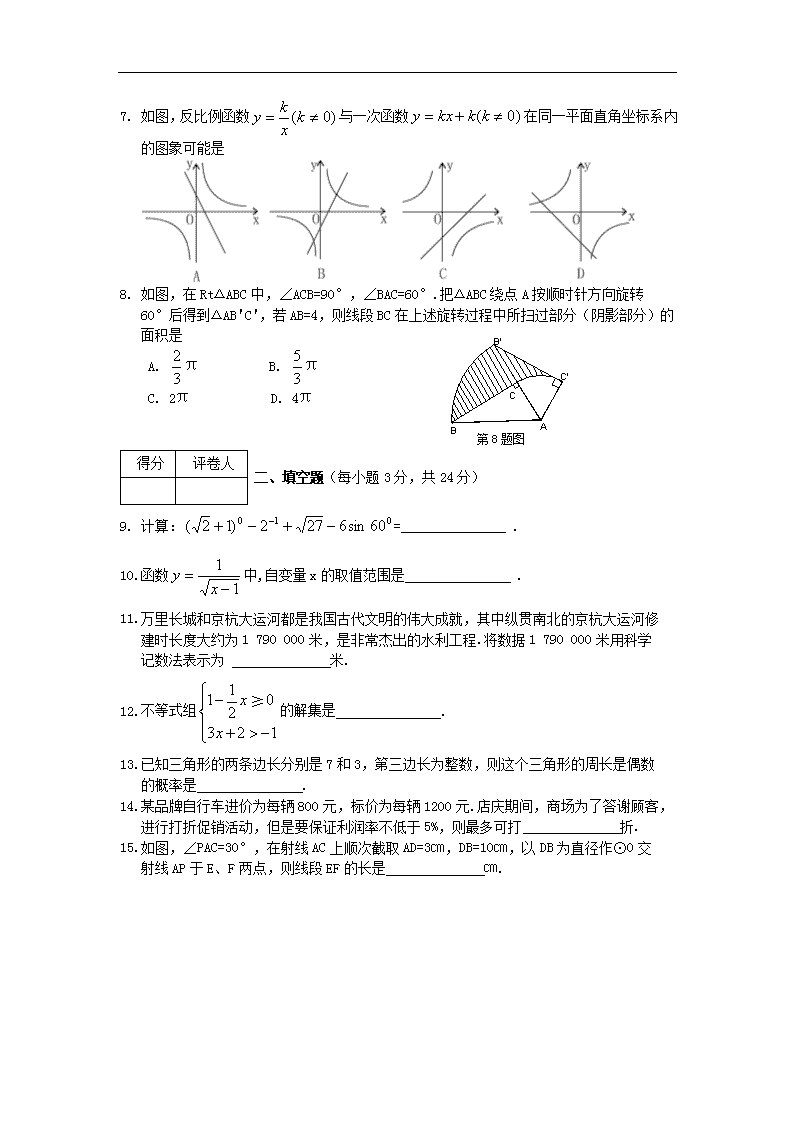下列说法正确的是 ‎ A.同位角相等 B.梯形对角线相等 C.等腰三角形两腰上的高相等 D.对角线相等且垂直的四边形是正方形 7. 如图，反比例函数与一次函数在同一平面直角坐标系内的图象可能是 ‎8. 如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°.把△ABC绕点A按顺时针方向旋转 第8题图 ‎60°后得到△AB＇C ＇，若AB=4，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是 A. π B. π C. 2π D. 4π 得分 评卷人 二、填空题（每小题3分，共24分）‎ ‎9. 计算：= .‎ ‎10.函数中,自变量x的取值范围是 .‎ ‎11.万里长城和京杭大运河都是我国古代文明的伟大成就，其中纵贯南北的京杭大运河修 建时长度大约为1 790 000米，是非常杰出的水利工程.将数据1 790 000米用科学 记数法表示为 米. ‎ ‎≥‎ ‎12.不等式组的解集是 .‎ ‎13.已知三角形的两条边长分别是7和3，第三边长为整数，则这个三角形的周长是偶数 的概率是 .‎ ‎14.某品牌自行车进价为每辆800元，标价为每辆1200元.店庆期间，商场为了答谢顾客，‎ 进行打折促销活动，但是要保证利润率不低于5%，则最多可打 折. 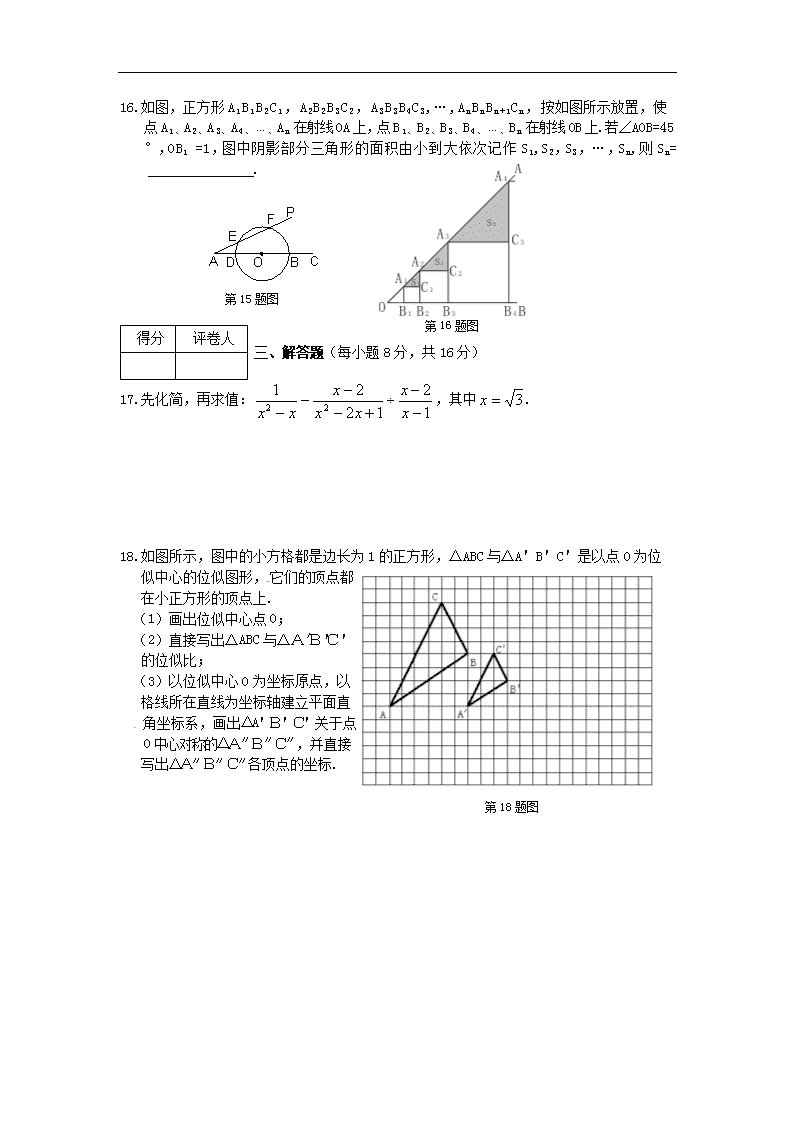‎ ‎15.如图，∠PAC=30°，在射线AC上顺次截取AD=3㎝，DB=10㎝，以DB为直径作⊙O交 射线AP于E、F两点，则线段EF的长是 ㎝.‎ 第16题图 ‎16.如图，正方形A1B1B2C1，A2B2B3C2，A3B3B4C3,…,AnBnBn+1Cn，按如图所示放置，使点A1、A2、A3、A4、…、An在射线OA上，点B1、B2、B3、B4、…、Bn在射线OB上.若∠AOB=45°，OB1 =1，图中阴影部分三角形的面积由小到大依次记作S1,S2，S3，…，Sn,则Sn=‎ ‎ .‎ 第15题图 得分 评卷人 三、解答题（每小题8分，共16分）‎ 17. 先化简，再求值：，其中.‎ ‎18.如图所示，图中的小方格都是边长为1的正方形，△ABC与△A＇B＇C＇是以点O第18题图 为位 ‎ 似中心的位似图形，它们的顶点都 ‎ 在小正方形的顶点上.‎ ‎（1）画出位似中心点O；‎ ‎（2）直接写出△ABC与△Ａ′Ｂ＇Ｃ＇‎ ‎ 的位似比；‎ ‎（3）以位似中心O为坐标原点，以 ‎ 格线所在直线为坐标轴建立平面直 ‎ 角坐标系，画出△A＇Ｂ＇Ｃ＇关于点 ‎ O中心对称的△Ａ″Ｂ″Ｃ″，并直接 ‎ 写出△Ａ″Ｂ″Ｃ″各顶点的坐标.‎ 得分 评卷人 四、解答题（每小题10分，共20分）‎ ‎19.随着人们生活水平的提高，城市家庭私家车的拥有量越来越多.私家车给人们的生活 带来很多方便，同时也给城市的道路交通带来了很大的压力,尤其是节假日期间交通 拥堵现象非常严重.为了缓解交通堵塞，尽量保持道路通畅，某市有关部门号召市民 ‎“在节假日期间选择公共交通工具出行”.为了了解市民的意见和态度，有关部门随 机抽取了若干市民进行了调查.经过统计、整理，制作统计图如下.请回答下列问题：‎ ‎ （1）这次抽查的市民总人数是多少？‎ ‎ （2）分别求出持“赞成”态度、“无所谓”态度的市民人数以及持“无所谓”态度的 ‎ 人数占总人数的百分比，并补全条形统计图和扇形统计图;‎ ‎ （3）若该市约有18万人，请估计对这一问题持“赞成”态度的人数约是多少？‎ 第19题图 ‎ ‎ ‎20.某部队要进行一次急行军训练，路程为32km.大部队先行，出发1小时后，由特种兵组成的突击小队才出发，结果比大部队提前20分钟到达目的地.已知突击小队的行进速度是大部队的1.5倍，求大部队的行进速度. （列方程解应用题）‎ 得分 评卷人 五、解答题（每小题10分，共20分）‎ ‎21.如图，有一个可以自由转动的转盘被平均分成五个扇形，五个扇形内部分别标有数字 ‎ 1、-2、3、-4、5.若将转盘转动两次，每一次停止转动后，指针指向的扇形内的数字 ‎ 分别记为m,n（当指针指在边界线时视为无效，重转），从而确定一个点的坐标为A（m,n）.‎ ‎ 请用列表或者画树状图的方法求出所有可能得到的点A的坐标，并求出点A在第一象 第21题图 ‎ 限内的概率.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎22.如图，大楼AB高16米，远处有一塔CD，某人在楼底B处测得塔顶的仰角为38.5°，‎ 爬到楼顶A处测得塔顶的仰角为22°，求塔高CD及大楼与塔之间的距离BD的长.‎ 第22 题图 ‎ (参考数据：sin22°≈0.37， cos22°≈0.93, tan22°≈0.40， sin38.5°≈0.62，cos38.5°≈0.78, tan38.5°≈0.80 )‎ 得分 评卷人 六、解答题（每小题10分，共20分）‎ 23. 如图：在△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D做直线DE垂直BC ‎ 于F，且交BA的延长线于点E.‎ ‎ （1）求证：直线DE是⊙O的切线；‎ ‎ （2）若cos∠BAC=，⊙O的半径为6，求线段CD的长. ‎ 第23题图 ‎ ‎ ‎ ‎ ‎ ‎ ‎24.某商店经营儿童益智玩具，已知成批购进时的单价是20元.调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件玩具售价不能高于40元. 设每件玩具的销售单价上涨了x元时（x为正整数），月销售利润为y元.‎ ‎ （1）求y与x的函数关系式并直接写出自变量x的取值范围.‎ ‎ （2）每件玩具的售价定为多少元时，月销售利润恰为2520元？‎ ‎ （3）每件玩具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？‎ 得分 评卷人 七、解答题（本题12分）‎ ‎25.已知：在△ABC中，∠BAC=90°,AB=AC，点D为直线BC上一动点（点D不与B、C重合）.以AD为边作正方形ADEF，连接CF. ‎ ‎(1)如图1，当点D在线段BC上时，求证：① BD⊥CF. ② CF=BC-CD.‎ ‎(2)如图2，当点D在线段BC的延长线上时，其它条件不变，请直接写出CF、BC、CD三条线段之间的关系；‎ ‎(3)如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状，并说明理由.‎ 第25题图 图2‎ 图3‎ 图1‎ 得分 评卷人 八、解答题（本题14分）‎ 26. 如图，抛物线交y轴于点C，直线 l为抛物线的对称轴，点P在第 ‎ 三象限且为抛物线的顶点.P到x轴的距离为，到y轴的距离为1.点C关于直线 ‎ l的对称点为A，连接AC交直线 l于B.‎ ‎ （1）求抛物线的表达式； ‎ ‎ （2）直线与抛物线在第一象限内交于点D，与y轴交于点F,连接BD交y轴于点E，且DE:BE=4:1.求直线的表达式；‎ ‎ （3）若N为平面直角坐标系内的点，在直线上是否存在点M，使得以点O、F、M、N为顶点的四边形是菱形？若存在，直接写出点M的坐标；若不存在，请说明理由.‎ 第26题图 ‎2012年锦州市数学试卷参考答案及评分标准 说明：此答案仅供参考，阅卷之前请做答案，答题中出现其他正确答案也可以得分。‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 B A D A A C D C 一、选择题 二、填空题 ‎9. 10. ＞1 11. 1.79×106 12. 13. ‎ ‎14. 七（写成数字“7”也正确） 15. 6 16. （，符合题意的答案即可）‎ 三、解答题 ‎17. 解：原式= ………………………2分 ‎ = ………………………3分 ‎ = ………………………5分 ‎ = ………………………6分 ‎ 当时，原式== ………………………8分 ‎18. （1）图中点O为所求（可以不写出结论，在图中画出 点O的正确位置即可） ………………2分 ‎（2）△ABC与△A＇B＇C＇的位似比等于2:1 ；‎ ‎………………3分 ‎（3）△A＇＇B＇＇C＇＇为所求（可以不写出结论，在图中画出 ‎△A＇＇B＇＇C＇＇即可）； ………………5分 A＇＇（6，0）； B＇＇（3，-2）； C＇＇（4，-4）.……………8分 四、解答题 ‎19. 解：‎ ‎（1）150÷30%=500（人）‎ ‎ 答：这次抽查的市民总人数是500人. ………2分 ‎(2) 持“赞成”态度的市民人数有：500×25%=125（人） ……3分 持“无所谓”态度的市民人数有：500-150-125=225（人）…4分 持“无所谓”态度的人数占总人数的百分比是：‎ ‎225÷500=45% . ……5分 统计图补充如图示. ……6分 ‎（3）180 000×25%=45 000（人）‎ 答：估计对这一问题持“赞成”态度的人数约为45 000人. …10分 ‎20. 解：设大部队的行进速度是x千米/小时.根据题意，得 …………… 1分 ‎1小时20分钟=小时 ‎ …………… 5分 解得 …………… 8分 经检验：是所列方程的解 …………… 9分 答：大部队的行进速度是8千米/小时. ……………10分 五、解答题 ‎21. 方法一：由题意可列表得：‎ ‎ 第一次(m)‎ 第二次(n)‎ ‎1‎ ‎-2‎ ‎3‎ ‎-4‎ ‎5‎ ‎1‎ ‎（1, 1）‎ ‎（-2， 1）‎ ‎（3， 1）‎ ‎（-4， 1）‎ ‎（5， 1）‎ ‎-2‎ ‎（1，-2）‎ ‎（-2，-2）‎ ‎（3，-2）‎ ‎（-4，-2）‎ ‎（5，-2）‎ ‎3‎ ‎（1, 3）‎ ‎（-2， 3）‎ ‎（3， 3）‎ ‎（-4， 3）‎ ‎（5， 3）‎ ‎-4‎ ‎（1，-4）‎ ‎（-2，-4）‎ ‎（3，-4）‎ ‎（-4，-4）‎ ‎（5，-4）‎ ‎5‎ ‎（1， 5）‎ ‎（-2， 5）‎ ‎（3， 5）‎ ‎（-4， 5）‎ ‎（5， 5）‎ ‎……………………… 7分 由表可知所有可能得到的点A的坐标共有25种，且每种结果发生的可能性相同，其中在第一象限内的结果有9种. ……………………… 8分 所以，P（点A在第一象限内）=. ………………………10分 方法二：根据题意画树状图如下：‎ ‎(3, 1)‎ ‎(3,-2)‎ ‎(3, 3)‎ ‎(3,-4)‎ ‎(3, 5)‎ ‎3‎ ‎(-4, 1)‎ ‎(-4,-2)‎ ‎(-4, 3)‎ ‎(-4,-4)‎ ‎(-4, 5)‎ ‎-4‎ ‎(5, 1)‎ ‎(5,-2)‎ ‎(5, 3)‎ ‎(5,-4)‎ ‎(5, 5)‎ ‎5‎ ‎(1, 1)‎ ‎(1,-2)‎ ‎(1, 3)‎ ‎(1,-4)‎ ‎(1, 5)‎ ‎1‎ ‎(-2, 1)‎ ‎(-2,-2)‎ ‎(-2, 3)‎ ‎(-2,-4)‎ ‎(-2, 5)‎ ‎-2‎ ‎……………………… 7分 由树状图可知所有可能得到的点A的坐标共有25种，且每种结果发生的可能性相同，其中在第一象限内的结果有9种. ………………8分 所以，P（点A在第一象限内）=. …………10分 ‎22.解：过点A作AE⊥CD于点E,由题意可知：∠CAE=22°，∠CBD=38.5°，ED=AB=16米 ‎ ‎ ‎ 设大楼与塔之间的距离BD的长为x米，则AE=BD=x(不设未知数x也可以) ……………………1分 ‎ ‎ ∵在Rt△BCD中,tan ∠CBD=‎ ‎∴CD=BD tan 38.5°≈0.8x………………………3分 ‎ ∵在Rt△ACE中,tan ∠CAE=‎ ‎∴CE=AE tan 22°≈0.4x（此处用“=” 不扣分）‎ ‎………………………5分 ‎∵CD-CE=DE ‎∴0.8x-0.4x=16 ………………………7分 ‎∴x=40‎ 即BD=40(米) ………………………8分 CD=0.8×40=32(米) ………………………9分 答：塔高CD是32米，大楼与塔之间的距离BD的长为40米. …………………10分 六、解答题 ‎23.方法一：（1）证明：连接BD、OD ‎ ∵AB是⊙O的直径 ‎∴∠ADB=90°则BD⊥AC ‎ ‎∵BA=BC ‎ ‎ ∴D为AC中点 ‎ ∵O是AB中点 ‎∴OD为△ABC的中位线 ‎∴OD∥BC ………3分 ‎∴∠BFE=∠ODE ‎∵DE⊥BC ‎∴∠BFE=90°‎ ‎∴∠ODE=90°‎ ‎∴OD⊥DE ‎∴直线DE是⊙O的切线 ……6分 ‎（2）解：∵⊙O的半径为6‎ ‎∴AB=12 ………7分 在Rt△ABD中 ‎∵cos∠BAC=‎ ‎∴AD=4 …………8分 由(1)知BD是△ABC的中线 ……9分 ‎∴CD=AD=4 …………10分 方法二：（1）证明：连接OD ‎∵OA=OD ‎∴∠OAD=∠ODA ‎∵AB=BC ‎∴∠BAC=∠ACB ‎∴∠ODA=∠ACB ‎∴OD∥BC ……………………3分 ‎∴∠ODE=∠BFE ‎∵DE⊥BC ‎∴∠BFE=90°‎ ‎∴∠ODE=90°‎ ‎∴OD⊥DE ‎∴直线DE是⊙O的切线 …………………………………………6分 ‎ (2)解：连接BD ‎ ∵⊙O的半径为6‎ ‎∴AB=12‎ ‎∵AB是⊙O的直径 ‎∴∠ADB=90° …………………………………………………7分 在Rt△ABD中 ‎∵cos∠BAC=‎ ‎∴AD=4 …………………………………………………8分 ‎∵∠ADB=90°‎ ‎∴BD⊥AC 又∵AB=BC ‎∴BD是△ABC的中线 ………………………………………………9分 ‎∴CD=AD=4 ……………………………………………10分 ‎24.解：（1）依题意得 ‎ ………………………2分 自变量x的取值范围是：0＜x≤10(1≤x≤10也正确)且x为正整数 ‎ ………………………3分 ‎（2）当y=2520时，得（元） ……………5分 ‎ 解得x1=2,x2=11（不合题意，舍去） ………6分 ‎ 当x=2时，30+x=32（元） ‎ ‎ 所以，每件玩具的售价定为32元时，月销售利润恰为2520元. ………7分 ‎ （3） ……………8分 ‎ ‎ ∵a=-10＜0 ∴当x=6.5时，y有最大值为2722.5 ……………9分 ‎∵0＜x≤10(1≤x≤10也正确)且x为正整数 ‎∴当x=6时，30+x=36,y=2720（元） 当x=7时，30+x=37,y=2720（元）‎ 所以，每件玩具的售价定为36元或37元时，每个月可获得最大利润.最大的月利润是2720元. …10分 七、解答题 ‎25. （1）①∵∠BAC=90°，AB=AC ‎∴∠ABC=∠ACB=45°‎ ‎∵四边形ADEF是正方形 ‎∴AD=AF，∠DAF=90°‎ ‎∵∠BAD=∠BAC-∠DAC ‎ ∠CAF=∠DAF-∠DAC ‎∴∠BAD=∠CAF ‎∴△BAD≌△CAF ………………………………3分 ‎∴∠ACF=∠ABD=45°，‎ ‎∴∠ACF+∠ACB=90° ‎ ‎∴BD⊥CF ………………………………4分 ‎ ② 由①△BAD≌△CAF可得BD= CF ‎∵BD=BC-CD ‎∴CF=BC-CD ………………………………6分 ‎ （2）CF=BC+CD ………………………………7分 ‎ （3）①CF=CD-BC ………………………………8分 ‎②∵∠BAC=90°，AB=AC ‎∴∠ABC=∠ACB=45°则∠ABD=180°-45°=135°‎ ‎∵四边形ADEF是正方形 ‎∴AD=AF，∠DAF=90°‎ ‎∵∠BAD=∠DAF -∠BAF ‎ ∠CAF=∠BAC -∠BAF ‎∴∠BAD=∠CAF ‎∴△BAD≌△CAF …………………………………9分 ‎∴∠ACF=∠ABD=180°-45°=135°‎ ‎∴∠FCD=∠ACF -∠ACB =90°则△FCD为直角三角形 ‎∵正方形ADEF中，O为DF中点 ‎∴OC=DF ………………………………10分 ‎∵在正方形ADEF中，OA=AE ，AE=DF ‎∴OC= OA ………………………………11分 ‎∴△AOC是等腰三角形 ……………………………12分 八、解答题 ‎26.解：（1）∵抛物线交y轴于点C ‎∴ C（0，-3）则 OC=3 ……………1分 ‎∵P到x轴的距离为，P到y轴的距离是1‎ ‎ 且在第三象限 ‎∴P（-1，-） ……………2分 ‎∵C关于直线l的对称点为A ‎∴A（-2，-3） ……………3分 将点A（-2，-3），P（-1，-）代入 有解得 ………………………5分 ‎∴抛物线的表达式为 ………………………6分 ‎（2）过点D做DG⊥y 轴于G，则∠DGE=∠BCE=90°‎ ‎∵∠DEG=∠BEC ‎∴△DEG∽△BEC ‎∵DE:BE=4:1‎ ‎∴ 则DG=4 ………………………7分 将x=4代入，得y=5‎ 则 D（4,5） ………………………8分 ‎∵过点D（4,5）‎ ‎∴ 则 m=2 ………………………9分 ‎∴所求直线的表达式为 ………………10分 ‎（3）存在 M1 M2 M3 M4…14分