- 248.97 KB
- 2021-11-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
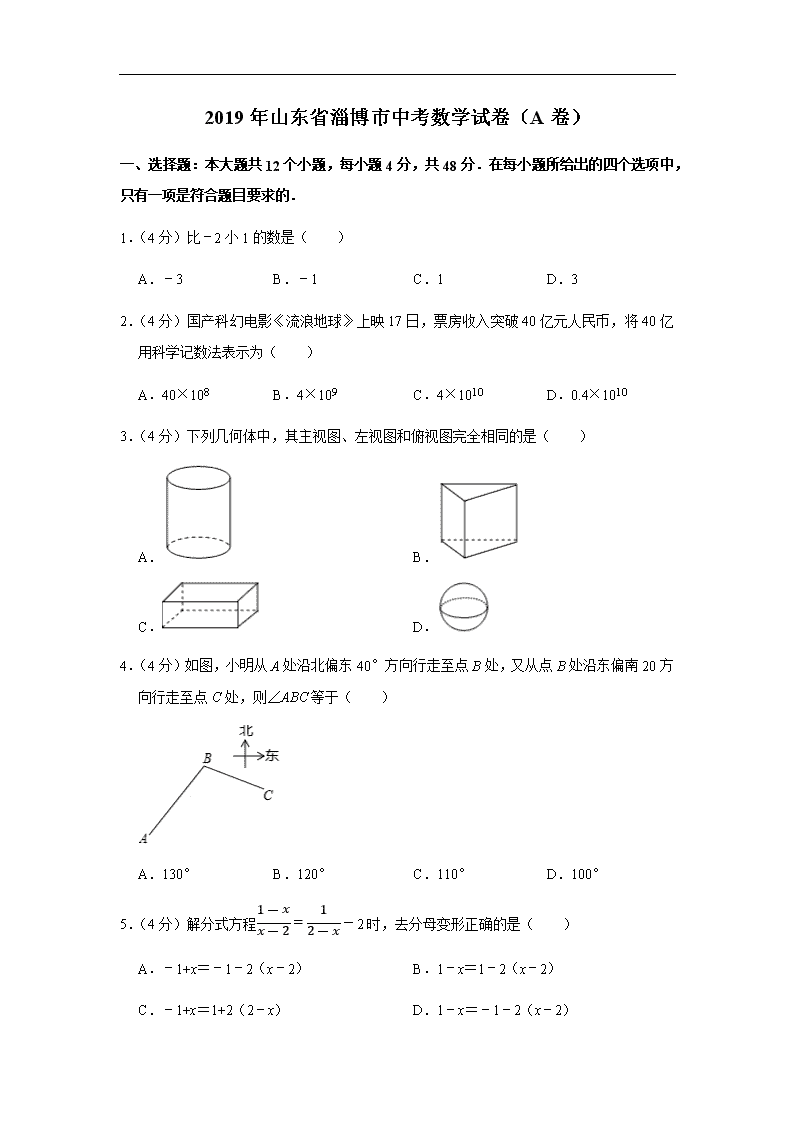
2019年山东省淄博市中考数学试卷(A卷)
一、选择题:本大题共12个小题,每小题4分,共48分.在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(4分)比﹣2小1的数是( )
A.﹣3 B.﹣1 C.1 D.3
2.(4分)国产科幻电影《流浪地球》上映17日,票房收入突破40亿元人民币,将40亿用科学记数法表示为( )
A.40×108 B.4×109 C.4×1010 D.0.4×1010
3.(4分)下列几何体中,其主视图、左视图和俯视图完全相同的是( )
A. B.
C. D.
4.(4分)如图,小明从A处沿北偏东40°方向行走至点B处,又从点B处沿东偏南20方向行走至点C处,则∠ABC等于( )
A.130° B.120° C.110° D.100°
5.(4分)解分式方程1-xx-2=12-x-2时,去分母变形正确的是( )
A.﹣1+x=﹣1﹣2(x﹣2) B.1﹣x=1﹣2(x﹣2)
C.﹣1+x=1+2(2﹣x) D.1﹣x=﹣1﹣2(x﹣2)
6.(4分)与下面科学计算器的按键顺序:
对应的计算任务是( )
A.0.6×65+124 B.0.6×56+124
C.0.6×5÷6+412 D.0.6×65+412
7.(4分)如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )
A.2 B.2 C.22 D.6
8.(4分)如图,在△ABC中,AC=2,BC=4,D为BC边上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为( )
A.2a B.52a C.3a D.72a
9.(4分)若x1+x2=3,x12+x22=5,则以x1,x2为根的一元二次方程是( )
A.x2﹣3x+2=0 B.x2+3x﹣2=0 C.x2+3x+2=0 D.x2﹣3x﹣2=0
二、填空题:本大题共5个小题,每小题4分,共20分.请直接填写最后结果.
10.(4分)单项式12a3b2的次数是 .
11.(4分)分解因式:x3+5x2+6x.
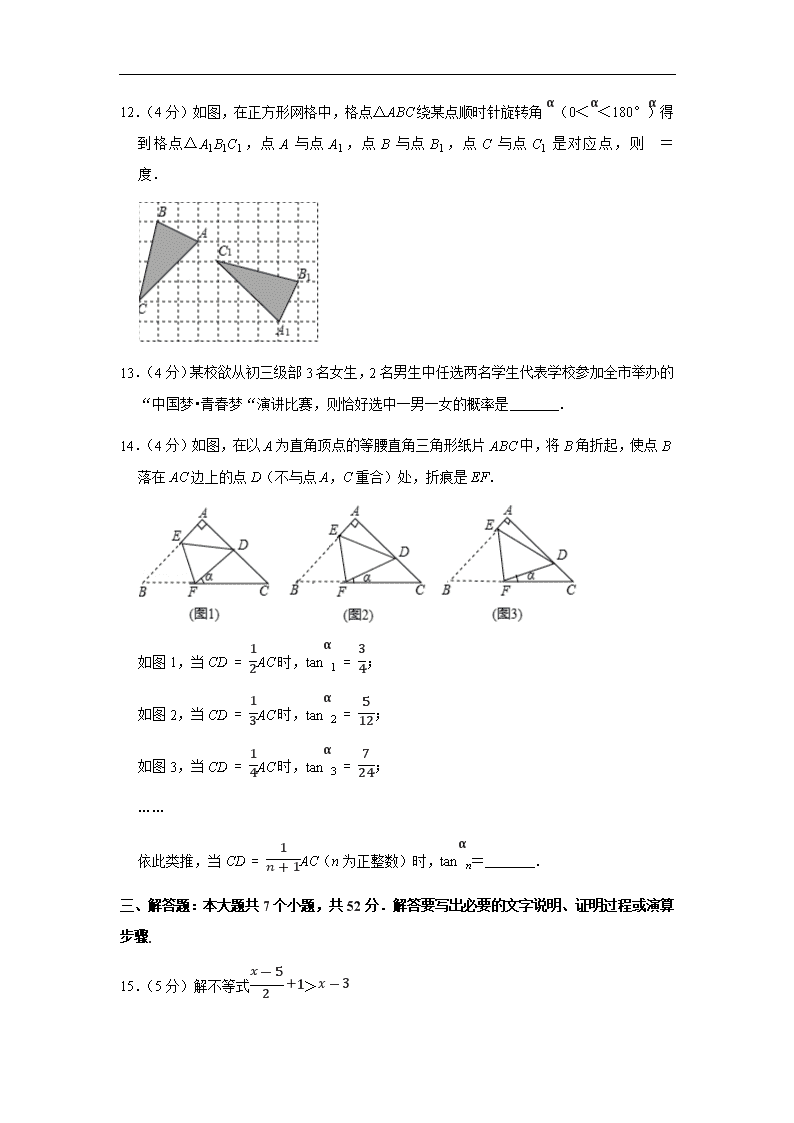
12.(4分)如图,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α= 度.
13.(4分)某校欲从初三级部3名女生,2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦“演讲比赛,则恰好选中一男一女的概率是 .
14.(4分)如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D(不与点A,C重合)处,折痕是EF.
如图1,当CD=12AC时,tanα1=34;
如图2,当CD=13AC时,tanα2=512;
如图3,当CD=14AC时,tanα3=724;
……
依此类推,当CD=1n+1AC(n为正整数)时,tanαn= .
三、解答题:本大题共7个小题,共52分.解答要写出必要的文字说明、证明过程或演算步骤.
15.(5分)解不等式x-52+1>x-3
16.(5分)已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.
17.(8分)文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别
年龄段
频数(人数)
第1组
10≤x<20
5
第2组
20≤x<30
a
第3组
30≤x<40
35
第4组
40≤x<50
20
第5组
50≤x<60
15
(1)请直接写出a= ,m=
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
18.(8分)“一带一路”促进了中欧贸易的发展,我市某机电公司生产的A,B两种产品在欧洲市场热销.今年第一季度这两种产品的销售总额为2060万元,总利润为1020万元(利润=售价﹣成本).其每件产品的成本和售价信息如下表:
A
B
成本(单位:万元/件)
2
4
售价(单位:万元/件)
5
7
问该公司这两种产品的销售件数分别是多少?
19.(8分)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.
(1)求证:①BC是⊙O的切线;
②CD2=CE•CA;
(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.
20.(9分)如图1,正方形ABDE和BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M,连接MD,MG,MB.
(1)试证明DM⊥MG,并求MBMG的值.
(2)如图2,将图1中的正方形变为菱形,设∠EAB=2α(0<α<90°),其它条件不变,问(1)中MBMG的值有变化吗?若有变化,求出该值(用含α的式子表示);若无变化,说明理由.
21.(9分)如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点D,满足DA=OA,过D作DG⊥x轴于点G,设△ADG的内心为I,试求CI的最小值.
2019年山东省淄博市中考数学试卷(A卷)
参考答案与试题解析
一、选择题:本大题共12个小题,每小题4分,共48分.在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(4分)比﹣2小1的数是( )
A.﹣3 B.﹣1 C.1 D.3
【解答】解:﹣2﹣1=﹣(1+2)=﹣3.
故选:A.
2.(4分)国产科幻电影《流浪地球》上映17日,票房收入突破40亿元人民币,将40亿用科学记数法表示为( )
A.40×108 B.4×109 C.4×1010 D.0.4×1010
【解答】解:40亿用科学记数法表示为:4×109,
故选:B.
3.(4分)下列几何体中,其主视图、左视图和俯视图完全相同的是( )
A. B.
C. D.
【解答】解:A、圆柱的主视图和左视图都是矩形,但俯视图也是一个圆形,不符合题意;
B、三棱柱的主视图和左视图、俯视图都不相同,不符合题意;
C、长方体的主视图和左视图是相同的,都为一个长方形,但是俯视图是一个不一样的长方形,不符合题意;
D、球的三视图都是大小相同的圆,符合题意.
故选:D.
4.(4分)如图,小明从A处沿北偏东40°方向行走至点B处,又从点B处沿东偏南20方向行走至点C处,则∠ABC等于( )
A.130° B.120° C.110° D.100°
【解答】解:如图:
∵小明从A处沿北偏东40°方向行走至点B处,又从点B处沿东偏南20方向行走至点C处,
∴∠DAB=40°,∠CBF=20°,
∵向北方向线是平行的,即AD∥BE,
∴∠ABE=∠DAB=40°,
∵∠EBF=90°,
∴∠EBC=90°﹣20°=70°,
∴∠ABC=∠ABE+∠EBC=40°+70°=110°,
故选:C.
5.(4分)解分式方程1-xx-2=12-x-2时,去分母变形正确的是( )
A.﹣1+x=﹣1﹣2(x﹣2) B.1﹣x=1﹣2(x﹣2)
C.﹣1+x=1+2(2﹣x) D.1﹣x=﹣1﹣2(x﹣2)
【解答】解:去分母得:1﹣x=﹣1﹣2(x﹣2),
故选:D.
6.(4分)与下面科学计算器的按键顺序:
对应的计算任务是( )
A.0.6×65+124 B.0.6×56+124
C.0.6×5÷6+412 D.0.6×65+412
【解答】解:与下面科学计算器的按键顺序对应的计算任务是0.6×56+124,
故选:B.
7.(4分)如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )
A.2 B.2 C.22 D.6
【解答】解:由题意可得,
大正方形的边长为8=22,小正方形的边长为2,
∴图中阴影部分的面积为:2×(22-2)=2,
故选:B.
8.(4分)如图,在△ABC中,AC=2,BC=4,D为BC边上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为( )
A.2a B.52a C.3a D.72a
【解答】解:∵∠CAD=∠B,∠ACD=∠BCA,
∴△ACD∽△BCA,
∴S△ACDS△BCA=(ACAB)2,即aS△BCA=14,
解得,△BCA的面积为4a,
∴△ABD的面积为:4a﹣a=3a,
故选:C.
9.(4分)若x1+x2=3,x12+x22=5,则以x1,x2为根的一元二次方程是( )
A.x2﹣3x+2=0 B.x2+3x﹣2=0 C.x2+3x+2=0 D.x2﹣3x﹣2=0
【解答】解:∵x12+x22=5,
∴(x1+x2)2﹣2x1x2=5,
而x1+x2=3,
∴9﹣2x1x2=5,
∴x1x2=2,
∴以x1,x2为根的一元二次方程为x2﹣3x+2=0.
故选:A.
二、填空题:本大题共5个小题,每小题4分,共20分.请直接填写最后结果.
10.(4分)单项式12a3b2的次数是 5 .
【解答】解:单项式12a3b2的次数是3+2=5.
故答案为5.
11.(4分)分解因式:x3+5x2+6x.
【解答】解:x3+5x2+6x,
=x(x2+5x+6),
=x(x+2)(x+3).
12.(4分)如图,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α= 90 度.
【解答】解:如图,
连接CC1,AA1,作CC1,AA1的垂直平分线交于点E,连接AE,A1E
∵CC1,AA1的垂直平分线交于点E,
∴点E是旋转中心,
∵∠AEA1=90°
∴旋转角α=90°
故答案为:90
13.(4分)某校欲从初三级部3名女生,2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦“演讲比赛,则恰好选中一男一女的概率是 35 .
【解答】解:画树状图为:
共20种等可能的结果数,其中选中一男一女的结果数为12,
∴恰好选中一男一女的概率是1220=35,
故答案为:35.
14.(4分)如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D(不与点A,C重合)处,折痕是EF.
如图1,当CD=12AC时,tanα1=34;
如图2,当CD=13AC时,tanα2=512;
如图3,当CD=14AC时,tanα3=724;
……
依此类推,当CD=1n+1AC(n为正整数)时,tanαn= 2n+12n2+2n .
【解答】解:观察可知,正切值的分子是3,5,7,9,…,2n+1,
分母与勾股数有关系,分别是勾股数3,4,5;5,12,13;7,24,25;9,40,41;…,2n+1,(2n+1)2-12,(2n+1)2+12中的中间一个.
∴tanαn=2n+1(2n+1)2-12=2n+12n2+2n.
故答案为:2n+12n2+2n.
三、解答题:本大题共7个小题,共52分.解答要写出必要的文字说明、证明过程或演算步骤.
15.(5分)解不等式x-52+1>x-3
【解答】解:将不等式x-52+1>x-3两边同乘以2得,
x﹣5+2>2x﹣6
解得x<3.
16.(5分)已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.
【解答】证明:∵∠BAE=∠DAC
∴∠BAE+∠CAE=∠DAC+∠CAE
∴∠CAB=∠EAD,且AB=AD,AC=AE
∴△ABC≌△ADE(SAS)
∴∠C=∠E
17.(8分)文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别
年龄段
频数(人数)
第1组
10≤x<20
5
第2组
20≤x<30
a
第3组
30≤x<40
35
第4组
40≤x<50
20
第5组
50≤x<60
15
(1)请直接写出a= 25 ,m= 20 ,第3组人数在扇形统计图中所对应的圆心角是 126 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
【解答】解:(1)a=100﹣5﹣35﹣20﹣15=25,
m%=(20÷100)×100%=20%,
第3组人数在扇形统计图中所对应的圆心角是:360°×35100=126°,
故答案为:25,20,126;
(2)由(1)值,20≤x<30有25人,
补全的频数分布直方图如右图所示;
(3)300×20100=60(万人),
答:40~50岁年龄段的关注本次大会的人数约有60万人.
18.(8分)“一带一路”促进了中欧贸易的发展,我市某机电公司生产的A,B两种产品在欧洲市场热销.今年第一季度这两种产品的销售总额为2060万元,总利润为1020万元(利润=售价﹣成本).其每件产品的成本和售价信息如下表:
A
B
成本(单位:万元/件)
2
4
售价(单位:万元/件)
5
7
问该公司这两种产品的销售件数分别是多少?
【解答】解:设A,B两种产品的销售件数分别为x件、y件;
由题意得:5x+7y=20602x+4y=2060-1020,
解得:x=160y=180;
答:A,B两种产品的销售件数分别为160件、180件.
19.(8分)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.
(1)求证:①BC是⊙O的切线;
②CD2=CE•CA;
(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.
【解答】解:(1)①连接OD,
∵AD是∠BAC的平分线,∴∠DAB=∠DAO,
∵OD=OA,∴∠DAO=∠ODA,
∴∠DAO=∠ADO,
∴DO∥AB,而∠B=90°,
∴∠ODB=90°,
∴BC是⊙O的切线;
②连接DE,
∵BC是⊙O的切线,∴∠CDE=∠DAC,
∠C=∠C,∴△CDE∽△CAD,
∴CD2=CE•CA;
(2)连接DE、OE,设圆的半径为R,
∵点F是劣弧AD的中点,∴是OF是DA中垂线,
∴DF=AF,∴∠FDA=∠FAD,
∵DO∥AB,∴∠PDA=∠DAF,
∴∠ADO=∠DAO=∠FDA=∠FAD,
∴AF=DF=OA=OD,
∴△OFD、△OFA是等边三角形,
∴∠C=30°,
∴OD=12OC=(OE+EC),而OE=OD,
∴CE=OE=R=3,
S阴影=S扇形DFO=60360×π×32=3π2.
20.(9分)如图1,正方形ABDE和BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M,连接MD,MG,MB.
(1)试证明DM⊥MG,并求MBMG的值.
(2)如图2,将图1中的正方形变为菱形,设∠EAB=2α(0<α<90°),其它条件不变,问(1)中MBMG的值有变化吗?若有变化,求出该值(用含α的式子表示);若无变化,说明理由.
【解答】(1)证明:如图1中,延长DM交FG的延长线于H.
∵四边形ABCD,四边形BCFG都是正方形,
∴DE∥AC∥GF,
∴∠EDM=∠FHM,
∵∠EMD=∠FMH,EM=FM,
∴△EDM≌△FHM(AAS),
∴DE=FH,DM=MH,
∵DE=2FG,BG=DG,
∴HG=DG,
∵∠DGH=∠BGF=90°,MH=DM,
∴GM⊥DM,DM=MG,
连接EB,BF,设BC=a,则AB=2a,BE=22a,BF=2a,
∵∠EBD=∠DBF=45°,
∴∠EBF=90°,
∴EF=BE2+BF2=10a,
∵EM=MF,
∴BM=12EF=102a,
∵HM=DM,GH=FG,
∴MG=12DF=22a,
∴BMMG=102a22a=5.
(2)解:(1)中MBMG的值有变化.
理由:如图2中,连接BE,AD交于点O,连接OG,CG,BF,CG交BF于O′.
∵DO=OA,DG=GB,
∴GO∥AB,OG=12AB,
∵GF∥AC,
∴O,G,F共线,
∵FG=12AB,
∴OF=AB=DF,
∵DF∥AC,AC∥OF,
∴DE∥OF,
∴OD与EF互相平分,
∵EM=MF,
∴点M在直线AD上,
∵GD=GB=GO=GF,
∴四边形OBFD是矩形,
∴∠OBF=∠ODF=∠BOD=90°,
∵OM=MD,OG=GF,
∴MG=12DF,设BC=m,则AB=2m,
易知BE=2OB=2•2m•sinα=4msinα,BF=2BO°=2m•cosα,DF=OB=2m•sinα,
∵BM=12EF=12BE2+BF2=4m2⋅sin2α+m2⋅cos2α,GM=12DF=m•sinα,
∴BMMG=4m2⋅sin2α+m2⋅cos2αm⋅sinα=4sin2α+cos2αsinα.
21.(9分)如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点D,满足DA=OA,过D作DG⊥x轴于点G,设△ADG的内心为I,试求CI的最小值.
【解答】解:(1)∵抛物线y=ax2+bx+3过点A(3,0),B(﹣1,0)
∴9a+3b+3=0a-b+3=0 解得:a=-1b=2
∴这条抛物线对应的函数表达式为y=﹣x2+2x+3
(2)在y轴上存在点P,使得△PAM为直角三角形.
∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴顶点M(1,4)
∴AM2=(3﹣1)2+42=20
设点P坐标为(0,p)
∴AP2=32+p2=9+p2,MP2=12+(4﹣p)2=17﹣8p+p2
①若∠PAM=90°,则AM2+AP2=MP2
∴20+9+p2=17﹣8p+p2
解得:p=-32
∴P(0,-32)
②若∠APM=90°,则AP2+MP2=AM2
∴9+p2+17﹣8p+p2=20
解得:p1=1,p2=3
∴P(0,1)或(0,3)
③若∠AMP=90°,则AM2+MP2=AP2
∴20+17﹣8p+p2=9+p2
解得:p=72
∴P(0,72)
综上所述,点P坐标为(0,-32)或(0,1)或(0,3)或(0,72)时,△PAM为直角三角形.
(3)如图,过点I作IE⊥x轴于点E,IF⊥AD于点F,IH⊥DG于点H
∵DG⊥x轴于点G
∴∠HGE=∠IEG=∠IHG=90°
∴四边形IEGH是矩形
∵点I为△ADG的内心
∴IE=IF=IH,AE=AF,DF=DH,EG=HG
∴矩形IEGH是正方形
设点I坐标为(m,n)
∴OE=m,HG=GE=IE=n
∴AF=AE=OA﹣OE=3﹣m
∴AG=GE+AE=n+3﹣m
∵DA=OA=3
∴DH=DF=DA﹣AF=3﹣(3﹣m)=m
∴DG=DH+HG=m+n
∵DG2+AG2=DA2
∴(m+n)2+(n+3﹣m)2=32
∴化简得:m2﹣3m+n2+3n=0
配方得:(m-32)2+(n+32)2=92
∴点I(m,n)与定点Q(32,-32)的距离为322
∴点I在以点Q(32,-32)为圆心,半径为322的圆在第一象限的弧上运动
∴当点I在线段CQ上时,CI最小
∵CQ=(32)2+(3+32)2=3102
∴CI=CQ﹣IQ=310-322
∴CI最小值为310-322.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/6/30 10:03:18;用户:中考培优辅导;邮箱:p5193@xyh.com;学号:27411521
相关文档
- 宿迁市中考数学试卷含答案解析2021-11-1023页
- 浙江省舟山市中考数学试卷含答案解2021-11-1023页
- 2019年四川省广安市中考数学试卷含2021-11-1025页
- 临沂市中考数学试卷含答案解析2021-11-1017页
- 2018年浙江省杭州市中考数学试卷含2021-11-0717页
- 2019年山东省聊城市中考数学试卷含2021-11-0730页
- 2018年上海市中考数学试卷含答案2021-11-066页
- 2018年湖北省黄冈市中考数学试卷含2021-11-0618页
- 2018年山东省潍坊市中考数学试卷含2021-11-0624页
- 2019年江苏省无锡市中考数学试卷含2021-11-0631页