2009中考数学分类汇编-猜想、探索规律型 15页

‎35．猜想、探索规律型 一、选择题 ‎1．(2009年四川省内江市)如图，小陈从O点出发，前进‎5米后向右转20O，‎ 再前进‎5米后又向右转20O，……，这样一直走下去，‎ O ‎20o ‎20o 他第一次回到出发点O时一共走了（ ）‎ A．‎60米 B．‎‎100米 C．‎90米 D．‎‎120米 ‎【答案】C.‎ ‎2．（2009年贵州黔东南州）某校生物教师李老师在生物实验室做试验时，将水稻种子分组进行发芽试验；第1组取3粒，第2组取5粒，第3组取7粒……即每组所取种子数目比该组前一组增加2粒，按此规律，那么请你推测第n组应该有种子数（ ）粒。‎ A、 B、 C、 D、‎ ‎【关键词】探索规律型 ‎【答案】A ‎3．（2009年江苏省）下面是按一定规律排列的一列数：‎ 第1个数：；‎ 第2个数：；‎ 第3个数：；‎ ‎……‎ 第个数：．‎ 那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）‎ A．第10个数 B．第11个数 C．第12个数 D．第13个数 ‎【答案】A ‎4．（2009年孝感）对于每个非零自然数n，抛物线与x轴交于An、Bn两点，以表示这两点间的距离，则的值是 A． B． C． D． ‎ ‎【答案】D ‎5．（2009年重庆）观察下列图形，则第个图形中三角形的个数是（ ）‎ ‎……‎ 第1个 第2个 第3个 A． B． C． D．‎ ‎【答案】D．‎ ‎6．(2009年河北)古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”． 从图7中可以发现，任何一个大于1‎ 的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）‎ ‎4=1+3 9=3+6 16=6+10‎ 图7‎ ‎…‎ A．13 = 3+10 B．25 = 9+16 ‎ C．36 = 15+21 D．49 = 18+31‎ ‎【答案】C 二、填空题 ‎1．(2009年四川省内江市)把一张纸片剪成4块，再从所得的纸片中任取若干块，每块又剪成4块，像这样依次地进行下去，到剪完某一次为止。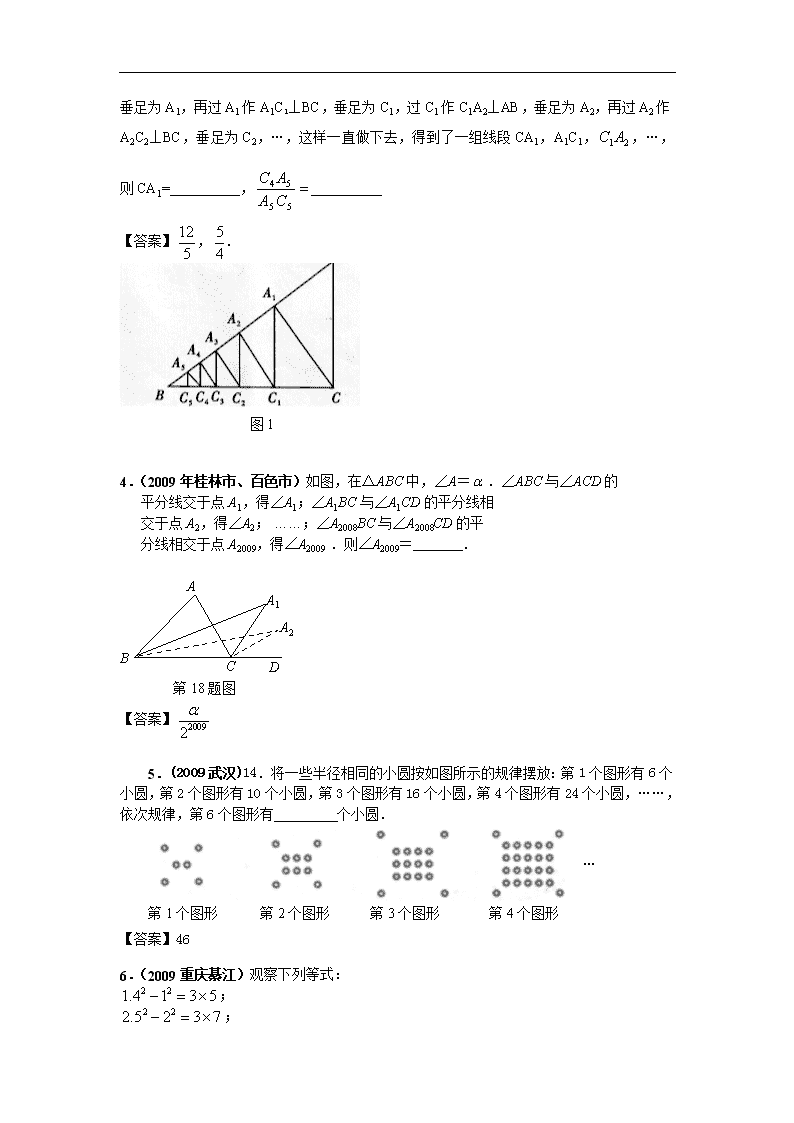那么2007，2008，2009，2010这四个数中______________可能是剪出的纸片数 ‎【答案】2008‎ ‎2．（2009仙桃）如图所示，直线y＝x＋1与y轴相交于点A1，以OA1为边作正方形OA1B‎1C1，记作第一个正方形；然后延长C1B1与直线y＝x＋1相交于点A2，再以C‎1A2为边作正方形C‎1A2B‎2C2，记作第二个正方形；同样延长C2B2与直线y＝x＋1相交于点A3，再以C‎2A3为边作正方形C‎2A3B‎3C3，记作第三个正方形；…依此类推，则第n个正方形的边长为________________．‎ ‎【答案】‎ ‎3．（2009年泸州）如图1，已知Rt△ABC中，AC=3，BC= 4，过直角顶点C作CA1⊥A B，垂足为A1，再过A1作A‎1C1⊥BC，垂足为C1，过C1作C‎1A2⊥AB，垂足为A2，再过A2作A‎2C2⊥BC，垂足为C2，…，这样一直做下去，得到了一组线段CA1，A‎1C1，，…，则CA1= ， ‎ ‎【答案】，.‎ 图1‎ ‎4．（2009年桂林市、百色市）如图，在△ABC中，∠A＝．∠ABC与∠ACD的 平分线交于点A1，得∠A1；∠A1BC与∠A1CD的平分线相 交于点A2，得∠A2； ……；∠A2008BC与∠A2008CD的平 分线相交于点A2009，得∠A2009 ．则∠A2009＝ ．‎ B A C D 第18题图 A1‎ A2‎ ‎【答案】‎ ‎5．(2009武汉)14．将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，……，依次规律，第6个图形有 个小圆．‎ 第1个图形 第2个图形 第3个图形 第4个图形 ‎…‎ ‎【答案】46 ‎ ‎6．（2009重庆綦江）观察下列等式：‎ ‎；‎ ‎；‎ ‎；‎ ‎…………‎ 则第（是正整数）个等式为________.‎ ‎【答案】‎ ‎7．(2009成都)已知，记，，…，，则通过计算推测出的表达式＝_______．‎ ‎(用含n的代数式表示)‎ ‎【答案】‎ ‎8．（2009年淄博市）如图，网格中的每个四边形都是菱形．如果格点三角形ABC的面积为S，按照如图所示方式得到的格点三角形A1B‎1C1的面积是，格点三角形A2B‎2C2的面积是19S，那么格点三角形A3B‎3C3的面积为 ．37S A A1‎ A2‎ A3‎ B3‎ B2‎ B1‎ B C1‎ C2‎ C3‎ ‎（第17题）‎ C ‎ ‎ ‎【答案】37S ‎9．（2009年娄底）王婧同学用火柴棒摆成如下的三个“中”字形图案，依此规律，第n个“中”字形图案需 根火柴棒. ‎【答案】6n+3或9+6（n-1）‎ ‎10（2009丽水市）如图，图①是一块边长为1，周长记为P1的正三角形纸板，沿图①的底边剪去一块边长为的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉正三角形纸板边长的）后，得图③，④，…，记第n(n≥3) 块纸板的周长为Pn，则Pn-Pn-1= ▲ .‎ ‎…‎ ‎① ② ③ ④ ‎ ‎【答案】‎ ‎11（2009恩施市）观察数表 ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎3‎ ‎6‎ ‎10‎ ‎15‎ ‎15‎ ‎5‎ A ‎1‎ ‎1‎ 根据表中数的排列规律，则字母所表示的数是____________．‎ ‎【答案】-10‎ ‎12．（2009年广西南宁）正整数按图8的规律排列．请写出第20行，第21列的数字 ．‎ 第一行 第二行 第三行 第四行 第五行 第一列 第二列 第三列 第四列 第五列 ‎1‎ ‎2‎ ‎5‎ ‎10‎ ‎17‎ ‎…‎ ‎4‎ ‎3‎ ‎6‎ ‎11‎ ‎18‎ ‎…‎ ‎9‎ ‎8‎ ‎7‎ ‎12‎ ‎19‎ ‎…‎ ‎16‎ ‎15‎ ‎14‎ ‎13‎ ‎20‎ ‎…‎ ‎25‎ ‎24‎ ‎23‎ ‎22‎ ‎21‎ ‎…‎ ‎……‎ 图8‎ ‎【答案】420‎ ‎13．(2009年牡丹江市)有一列数…，那么第7个数是 ．‎ ‎【答案】‎ ‎14．（2009年广州市）如图7-①，图7-②，图7-③，图7-④，…，是用围棋棋子按照某种规律摆成的一行“广”字，按照这种规律，第5个“广”字中的棋子个数是________，第个“广”字中的棋子个数是________‎ ‎【答案】‎ ‎15．（2009年益阳市）图6是一组有规律的图案，第1个 图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第(n是正整数)个图案中由 个基础图形组成．‎ 图6‎ ‎(1)‎ ‎(2)‎ ‎(3)‎ ‎……‎ ‎-‎ ‎【答案】3n+1‎ ‎16．（2009年济宁市）观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形有 个 ．‎ ‎【答案】121‎ ‎17．（2009年宜宾）如图，菱形ABCD的对角线长分别为，以菱形ABCD各边的中点为顶点作矩形A1B‎1C1D1，然后再以矩形A1B‎1C1D1的中点为顶点作菱形A2B‎2C2D2，……，如此下去，得到四边形A2009B‎2009C2009D2009的面积用含 的代数式表示为 ．‎ ‎【答案】．‎ ‎18．（2009年日照）正方形A1B‎1C1O，A2B‎2C2C1，A3B‎3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线(k＞0)和x轴上，已知点B1(1，1)，B2(3，2)， ‎ 则Bn的坐标是______________． ‎ y x O C1‎ B2‎ A2‎ C3‎ B1‎ A3‎ B3‎ A1‎ C2‎ ‎（第17题图）‎ ‎【答案】(,).‎ ‎19．（2009年广西钦州）一组按一定规律排列的式子：－，，－，，…，（a≠0）则第n个式子是_▲_（n为正整数）．‎ ‎【答案】‎ ‎20．（2009年广西梧州）图（3）是用火柴棍摆成的边长分别是1，2，3 根火柴棍时的正方形．当边长为n根火柴棍时，设摆出的正方形所用的火柴棍的根数为，则＝ ★ ． （用n的代数式表示）‎ ‎……‎ n=1‎ n=2‎ n=3‎ ‎【答案】‎ ‎21．（2009肇庆）15．观察下列各式：，，，…，根据观察计算：＝ ．（n为正整数）‎ ‎【答案】‎ ‎22．(2009年湖州) 如图，已知，是斜边的中点，过作于，连结交于；过作于，连结交于；过作于，…，如此继续，可以依次得到点，…，，分别记…，的面积为，….则=________（用含的代数式表示）.‎ B C A E1‎ E2‎ E3‎ D4‎ D1‎ D2‎ D3‎ ‎【答案】‎ ‎23．(2009年咸宁市)如图所示的运算程序中，若开始输入的值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，……第2009次输出的结果为___________．‎ ‎【答案】3‎ ‎（第1４题）‎ 输入 ‎+3‎ 输出 为偶数 为奇数 ‎24．（2009年湖北荆州）13．将四张花纹面相同的扑克牌的花纹面都朝上，两张一叠放成两堆不变．若每次可任选一堆的最上面的一张翻看（看后不放回），并全部看完，则共有 种不同的翻牌方式．‎ ‎【答案】‎ ‎25．（2009年广东省）用同样规格的黑白两种颜色的正方形瓷砖，按下图的方式铺地板，则第（3）个图形中有黑色瓷砖 __________块，第个图形中需要黑色瓷砖__________块（用含的代数式表示）．‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎【答案】10，‎ ‎26．（2009年山西省）下列图案是晋商大院窗格的一部分，其中“○”代表窗纸上所贴的剪纸，则第个图中所贴剪纸“○”的个数为 ．‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎……‎ ‎……‎ ‎【答案】‎ ‎27．（2009 黑龙江大兴安岭）如图，边长为1的菱形中，．连结对角线，以为边作第二个菱形，使 ；连结，再以为边作第三个菱形，使 ；……，按此规律所作的第个菱形的边长为 ．‎ ‎【关键词】菱形的性质与判定 ‎【答案】‎ ‎28．(2009年本溪)16．如图所示，已知：点，，在内依次作等边三角形，使一边在轴上，另一个顶点在边上，作出的等边三角形分别是第1个，第2个，第3个，…，则第个等边三角形的边长等于 ． ‎ O y x ‎(A)‎ A1‎ C ‎1‎ ‎1‎ ‎2‎ B A2‎ A3‎ B3‎ B2‎ B1‎ ‎16题图 ‎【答案】‎ ‎29．观察下表，回答问题：‎ 序号 ‎1‎ ‎2‎ ‎3‎ ‎…‎ 图形 ‎…‎ 第 个图形中“△”的个数是“○”的个数的5倍．‎ ‎【答案】20‎ ‎30．（2009年绵阳市）将正整数依次按下表规律排成四列，则根据表中的排列规律，数2009应排的位置是第 行第 列．‎ 第1列 第2列 第3列 第4列 第1行 ‎1‎ ‎2‎ ‎3‎ 第2行 ‎6‎ ‎5‎ ‎4‎ 第3行 ‎7‎ ‎8‎ ‎9‎ 第4行 ‎12‎ ‎11‎ ‎10‎ ‎……‎ ‎【答案】670，3‎ ‎31．（2009年铁岭市）如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第个图形需要黑色棋子的个数是 ．‎ 第2个图形 第1个图形 第4个图形 第3个图形 ‎1‎ ‎【答案】或或 ‎32．（2009年青海）观察下面的一列单项式：，，，，…根据你发现的规律，第7个单项式为 ；第个单项式为 ‎ ‎【答案】；‎ ‎33．（2009年龙岩）观察下列一组数：，，，，…… ，它们是按一定规律排列的． 那么这一组数的第k个数是 ．‎ ‎【答案】‎ ‎34．(2009年抚顺市)观察下列图形（每幅图中最小的三角形都是全等的），请写出第个图中最小的三角形的个数有 个．‎ 第1个图 第2个图 第3个图 第4个图 ‎35． (2009年梅州市)如图5，每一幅图中有若干个大小不同的菱形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第4幅图中有 个，第n幅图中共有 个．‎ ‎…‎ ‎…‎ 第1幅 第2幅 第3幅 第n幅 图5‎ 三、解答题 ‎1．（2009仙桃）如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE绕A点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM＝BD，EN＝CE，得到图③，请解答下列问题：‎ ‎(1)若AB＝AC，请探究下列数量关系：‎ ‎①在图②中，BD与CE的数量关系是________________；‎ ‎②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；‎ ‎(2)若AB＝k·AC(k＞1)，按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN与∠BAC的数量关系，直接写出你的猜想，不必证明．‎ ‎【答案】解：（1）①BD=CE；②AM=AN，∠MAN=∠BAC.‎ ‎（2）AM=AN，∠MAN=∠BAC.‎ ‎2．（2009年台州市）将正整数1，2，3，…从小到大按下面规律排列．若第4行第2列的数为32，则 ‎① ；②第行第列的数为 （用，表示）．‎ ‎ 　　 　　　 ‎ 第列 第列 第列 ‎…‎ 第列 第行 ‎1‎ ‎…‎ 第行 ‎…‎ 第行 ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎【答案】10，（第一空2分，第二空3分；答给3分，答给2分）‎ ‎3．（2009年杭州市）如图，在等腰梯形ABCD中，∠C=60°，AD∥BC，且AD=DC，E、F分别在AD、DC的延长线上，且DE=CF，AF、BE交于点P．‎ ‎（1）求证：AF=BE；‎ D E F P B A ‎（第22题）‎ C ‎（2）请你猜测∠BPF的度数，并证明你的结论．‎ ‎【答案】（1）BE=AF；‎ ‎（2）猜想∠BPF=120° .‎ ‎4．（2009恩施市）D A C B E F 图9‎ 宽与长之比为∶‎ 的矩形叫黄金矩形，黄金矩形令人赏心悦目，它给我们以协调，匀称的美感，如图9，如果在一个黄金矩形里画一个正方形，那么留下的矩形还是黄金矩形吗？请证明你的结论．‎ ‎【答案】解: 留下的矩形CDFE是黄金矩形 。‎ ‎5．（2009白银市）29．本试卷第19题为：若，，试不用将分数化小数的方法比较a、b的大小．‎ 观察本题中数a、b的特征，以及你比较大小的过程，直接写出你发现的一个一般结论．‎ ‎【答案】29．解：学生可能写出不同程度的一般的结论，由一般化程度不同得不同分．‎ 若m、n是任意正整数，且m＞n，则．‎ 若m、n是任意正实数，且m＞n，则．‎ 若m、n、r是任意正整数，且m＞n；或m、n是任意正整数，r是任意正实数，且m＞n，则．‎ 若m、n是任意正实数，r是任意正整数，且m＞n；或m、n、r是任意正实数，且m＞n，则．‎ ‎6．（2009年衢州）如图，AD是⊙O的直径．‎ ‎(1)　如图①，垂直于AD的两条弦B‎1C1，B‎2C2把圆周4等分，则∠B1的度数是　　　　　　，∠B2的度数是　　　　　　；‎ ‎(2)　如图②，垂直于AD的三条弦B‎1C1，B‎2C2，B‎3C3把圆周6等分，分别求∠B1，∠B2，‎ ‎∠B3的度数；‎ ‎(3)　如图③，垂直于AD的n条弦B‎1C1，B‎2C2，B‎3 C3，…，BnCn把圆周2n等分，请你用含n的代数式表示∠Bn的度数(只需直接写出答案)．‎ A O D B1‎ B2‎ C1‎ C2‎ 图①‎ O D A B1‎ C1‎ B2‎ C2‎ C3‎ B3‎ 图②‎ D Bn A O B1‎ Bn-2‎ C1‎ B2‎ C2‎ B3‎ C3‎ Cn-2‎ Bn-1‎ Cn-1‎ Cn ‎……‎ 图③‎ ‎【答案】解：(1)　22.5°，67.5° ‎ ‎(2)　 45°， 75°．‎ ‎(3)　 ．(或) ‎ ‎7．（2009年安徽）19．学校植物园沿路护栏纹饰部分设计成若干个全等菱形图案，每增加一个菱形图案，纹饰长度就增加dcm，如图所示．已知每个菱形图案的边长cm，其一个内角为60°．‎ ‎60°‎ ‎……‎ d L ‎（1）若d＝26，则该纹饰要231个菱形图案，求纹饰的长度L；‎ ‎（2）当d＝20时，若保持（1）中纹饰长度不变，则需要多少个这样的菱形图案？‎ ‎【答案】（1）‎6010 cm（2）需300个这样的菱形图案．‎