【40套试卷合集】河北省沧州沧县联考2019-2020学年数学九上期末模拟试卷含答案 10页

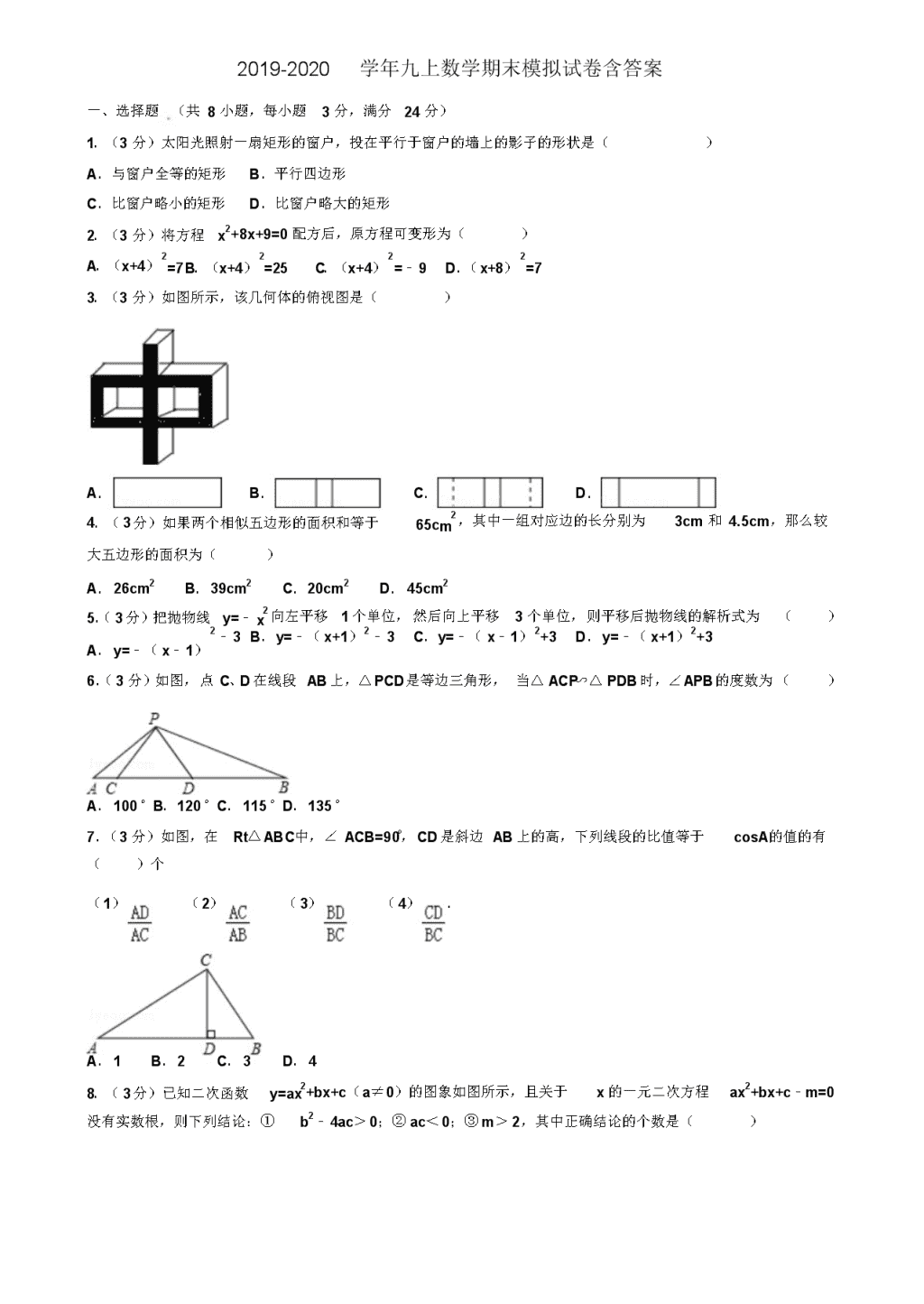
‎2019-2020 学年九上数学期末模拟试卷含答案 一、选择题 （共 8 小题，每小题 3 分，满分 24 分）‎ ‎1．（ 3 分）太阳光照射一扇矩形的窗户，投在平行于窗户的墙上的影子的形状是（ ）‎ A．与窗户全等的矩形 B．平行四边形 C．比窗户略小的矩形 D．比窗户略大的矩形 ‎2．（ 3 分）将方程 x2+8x+9=0 配方后，原方程可变形为（ ）‎ A．（ x+4）‎ ‎2‎ ‎=7 B．（ x+4）‎ ‎2‎ ‎=25 C．（ x+4）‎ ‎2 2‎ ‎=﹣ 9 D．（ x+8） =7‎ ‎3．（ 3 分）如图所示，该几何体的俯视图是（ ）‎ A． B．‎ ‎4．（ 3 分）如果两个相似五边形的面积和等于 C．‎ ‎65c D．‎ ‎2 ，其中一组对应边的长分别为 3cm 和 4.5cm，那么较 大五边形的面积为（ ）‎ ‎2 2 2‎ ‎2‎ m A． 26cm ‎B． 39cm ‎C． 20cm ‎D． 45cm x ‎5．（ 3 分）把抛物线 y=﹣ 2 向左平移 1 个单位， 然后向上平移 3 个单位， 则平移后抛物线的解析式为 （ ）‎ ‎2﹣ 3 B． y=﹣（ x+1） 2﹣ 3 C． y=﹣（ x﹣ 1） 2+3 D． y=﹣（ x+1） 2+3‎ A． y=﹣（ x﹣ 1）‎ ‎6．（ 3 分）如图，点 C、D 在线段 AB 上，△ PCD 是等边三角形， 当△ ACP∽△ PDB 时，∠ APB 的度数为 （ ）‎ A． 100 °B． 120 °C． 115 °D． 135 °‎ ‎7．（ 3 分）如图，在 Rt△ ABC中，∠ ACB=90°， CD 是斜边 AB 上的高，下列线段的比值等于 cosA的值的有 ‎（ ）个 ‎（ 1） （ 2） （ 3） （ 4） ．‎ A． 1 B． 2 C． 3 D． 4‎ ‎8．（ 3 分）已知二次函数 y=ax ‎2+bx+c（ a≠ 0）的图象如图所示，且关于 x 的一元二次方程 ax2+bx+c﹣m=0‎ 没有实数根，则下列结论：① b2﹣ 4ac＞ 0；② ac＜ 0；③ m＞ 2，其中正确结论的个数是（ ）‎ A． 0 B． 1 C． 2 D． 3‎ 二、填空题（共 6 小题，每小题 3 分，满分 18 分）‎ ‎9．（ 3 分）小明和小红在阳光下行走，小明身高 1.75 米，他的影长 2.0 米，小红比小明矮 7 厘米，此刻小 红的影长是 米．‎ ‎10 ．（ 3 分）若 ‎=2，则 ‎=‎ ‎．‎ ‎11 ．（ 3 分）某校去年对实验器材的投资为 2 万元，预计今明两年的投资总额为 8 万元，若设该校这两年 在实验器材投资上的平均增长率为 x，则可列方程： ．‎ ‎12 ．（ 3 分）如图，小明晚上由路灯 A 下的 B 处走到 C 处时，测得影长 CD 的长为 1m ，从 C处继续往前走 ‎3m 达到 E 处时， 测得影子 EF的长为 2m，已知小明的身高时 1.5m，那么路灯 A 的高度 AB 等于 m．‎ y=ax ‎13 ．（ 3 分）下表是二次函数 2+bx+c 的自变量 x 和因变量 y 的对应值表：‎ x ﹣ 3 ﹣ 2 ﹣ 1 0 1 2 3‎ y 12 5 0 ﹣ 3 ﹣ 4 ﹣ 3 0‎ 若点 A（ x1，y1）、B（ x2，y2 ）都在这个二次函数的图象上， 且 3＜ x1＜ x2 ，则 y1、y2 的大小关 系是 y1 y2，．（ 填 写 “＜ ”， “＞ ”或 “=）”‎ ‎14 ．（ 3 分）如图， 10 个边长为 1 的正方形摆放在平面直角坐标系中，经过 A（ 1， 0）点的一条直线 1 将 这 10 个正方形分成面积相等的两部分，则该直线的解析式为 ．‎ 三、解答题（共 10 小题，满分 78 分）‎ ‎15 ．（ 4 分）如图，有一块三角形的铁皮 求作：以∠ C 为一个内角的菱形 CEFG，使顶点 F 在 AB 边上 要求：尺规作图，不写作法，保留作图痕迹．‎ ‎16 ．（ 8 分）解方程 ‎（ 1） x2﹣ 2x﹣2=0‎ ‎=4（ x﹣ 1）‎ ‎（ 2）（ x+1） 2 2．‎ ‎17．（ 6 分）小明和小刚做游戏一个不透明的布袋里装有 4 个大小、质地均相同的乒乓球，球上分别标有 数字 1， 2， 3， 4，随机从布袋中摸出一个乒乓球，记下数字后放回布袋里，再随机从布袋中摸出一个乒 乓球， 若这两个乒乓球上的数字之和能被 4 整除则小明赢； 若两个乒乓球上的数字之和能被 5 整除则小刚 赢；这个一个对游戏双方公平的游戏吗？请列表格或画树状图说明理由．‎ ‎18 ．（ 6 分）小鹏学完解直角三角形知识后，给同桌小艳出了一道题： “如图所示，把一张长方形卡片 ABCD 放在每格宽度为 12mm 的横格纸中，恰好四个顶点都在横格线上，已知 α=36°，求长方形卡片的周长． ” 请你帮小艳解答这道题． （精确到 1mm）（参考数据： sin36 °≈ 0.60， cos36°≈ 0.80， tan36°≈ 0.75）‎ ‎19 ．（ 6 分）环保局对某企业排污情况进行检测，结果显示，所排污水中硫化物的浓度超标，即硫化物的 浓度超过最高允许的 1.0mg/L ，环保局要求该企业立即整改，在 15 天以内（含 15 天）排污达标，整改过 程中，所排污水中硫化物的浓度 γ（ mg/L）与时间 x（天）的变化规律如图所示，其中线段 AB 表示前 3 天的变化规律，从第 3 天起，所排污水中硫化物的浓度 γ与时间 x 成反比例关系 ‎（ 1）求整改过程中硫化物的浓度 γ与时间 x 的函数表达式（要求标注自变量 x 的取值范围）‎ ‎（ 2）该企业所排污水中硫化物的浓度，能否在 15 天以内（含 15 天）排污达标？为什么？‎ ‎20．（ 8 分）如图， C 地在 A 地的正东方向，因有大山阻隔，由 A 地到 C 地需要绕行附近的 B 地，已知 B 地位于 A 地的北偏东 67°方向，距离 A 地 520km， C 地位于 B 地南偏西 30°方向，若要打通穿山隧道建高 铁，求线段 AC的长（结果保留整数） （参考数据： ≈ 1.73， sin67 °≈ ， cos67°≈ ， tan67°≈ ）‎ ‎21 ．（ 8 分）如图，△ ABC 中， AB=AC，点 D、 O 分别为 BC、 AB 的中点，连接并延长 DO 到点 E，使 AE∥ BC．‎ ‎（ 1）求证：四边形 AEBD是矩形；‎ ‎（ 2）当△ ABC满足什么条件时，矩形 AEBD是正方形？证明你的结论．‎ ‎22 ．（ 10 分）某店尝试用单价随天数而变化的销售模式销售一种商品，利用 30 天的时间销售一种成本为 ‎10 元 / 件的商品，经过统计得到此商品单价在第 x 天（ x 为正整数）销售的相关信息，如表所示： 销售量 n（件） n=50﹣ x 销售单价 m（元 / 件） m=20+ x ‎（ 1）请计算第几天该商品单价为 25 元 / 件？‎ ‎（ 2）求店销售该商品 30 天里所获利润 y（元）关于 x（天）的函数关系式；‎ ‎（ 3）这 30 天中第几天获得的利润最大？最大利润是多少？‎ ‎23 ．（ 10 分）探究活动一：‎ 如图 1，正方形 ABCD 和正方形 QMNP，∠ M= ∠ B， M 是正方形 ABCD的对称中心， MN 交 AB 于 F， QM 交 AD 于 E，线段 ME 与线段 MF 的数量关系是 ．（不必证明，直接给出结论即可） 探究活动二：‎ 如图 2，将上题中的 “正方形 ”改为 “矩形 ”，且 AB=mBC，其他条件不变（矩形 ABCD和矩形 QMNP，∠ M=‎ ‎∠ B， M 是矩形 ABCD的对称中心， MN 交 AB 于 F，QM 交 AD 于 E），探究并证明线段 ME 与线段 MF 的数 量关系；‎ 探究活动三：‎ 根据前面的探索和图 3，平行四边形 ABCD和平行四边形 QMNP 中，若 AB=mBC，∠ M=∠ B， M 是平行四 边形 ABCD的对称中心， MN 交 AB 于 F， QM 交 AD 于 E，请探究并证明线段 ME 与线段 MF 的数量关系．‎ ‎24 ．（ 12 分）如图 1，正方形 ABCD中， AB=4cm，点 P 从点 D 出发沿 DA 向点 A 匀速运动，速度是 1cm/s， 同时，点 Q 从点 A 出发沿 AB 方向，向点 B 匀速运动，速度是 2cm/s，连接 PQ、 CP、 CQ，设运动时间为 t（ s）（ 0＜ t＜ 2）‎ ‎（ 1）是否存在某一时刻 t，使得 PQ∥ BD？若存在，求出 t 值；若不存在，说明理由 ‎（ 2）设△ PQC的面积为 s（ cm2），求 s 与 t 之间的函数关系式；‎ ‎（ 3）如图 2，连接 AC，与线段 PQ 相交于点 M ，是否存在某一时刻 t ，使 S△ QCM： S△PCM=3： 5？若存在， 求出 t 值；若不存在，说明理由．‎ 参考答案与试题解析 一、选择题（共 8 小题，每小题 3 分，满分 24 分）‎ ‎1．（ 3 分）太阳光照射一扇矩形的窗户，投在平行于窗户的墙上的影子的形状是（ ）‎ A．与窗户全等的矩形 B．平行四边形 C．比窗户略小的矩形 D．比窗户略大的矩形 ‎【解答】解：太阳光照射一扇矩形的窗户，投在平行于窗户的墙上的影子的形状是与窗户全等的矩形． 故选： A．‎ x ‎2．（ 3 分）将方程 2+8x+9=0 配方后，原方程可变形为（ ）‎ A．（ x+4）‎ ‎2‎ ‎=7 B．（ x+4）‎ ‎2‎ ‎=25 C．（ x+4）‎ ‎2 2‎ ‎=﹣ 9 D．（ x+8） =7‎ ‎【解答】解： x2+8x=﹣ 9，‎ x ‎2+8x+16=7，‎ ‎=7．‎ ‎（ x+4） 2‎ 故选： A．‎ ‎3．（ 3 分）如图所示，该几何体的俯视图是（ ）‎ A． B． C． D．‎ ‎【解答】解：从上往下看，可以看到选项 C 所示的图形． 故选： C．‎ ‎65cm ‎4．（ 3 分）如果两个相似五边形的面积和等于 2 ，其中一组对应边的长分别为 3cm 和 4.5cm，那么较 大五边形的面积为（ ）‎ ‎2‎ A． 26cm ‎2‎ B． 39cm ‎2‎ C． 20cm ‎2‎ D． 45cm ‎= ．‎ ‎【解答】解：设较大五边形与较小五边形的面积分别是 m， n．则 =（ ） 2‎ 因而 n= m．‎ 根据面积之和是 65cm2．得到 m+ m=65， 解得： m=45，‎ 即较大五边形的面积为 45cm2． 故选： D．‎ x ‎5．（ 3 分）把抛物线 y=﹣ 2 向左平移 1 个单位， 然后向上平移 3 个单位， 则平移后抛物线的解析式为 （ ）‎ ‎2﹣ 3 B． y=﹣（ x+1） 2﹣ 3 C． y=﹣（ x﹣ 1） 2+3 D． y=﹣（ x+1） 2+3‎ A． y=﹣（ x﹣ 1）‎ ‎【解答】解：当 y=﹣ x2 向左平移 1 个单位时，顶点由原来的（ 0，0）变为（﹣ 1， 0）， 当向上平移 3 个单位时，顶点变为（﹣ 1，3），‎ 则平移后抛物线的解析式为 y=﹣（ x+1） 2+3． 故选： D．‎ ‎6．（ 3 分）如图，点 C、D 在线段 AB 上，△ PCD 是等边三角形， 当△ ACP∽△ PDB 时，∠ APB 的度数为 （ ）‎ A． 100 °B． 120 °C． 115 °D． 135 °‎ ‎【解答】解：∵△ ACP∽△ PDB，‎ ‎∴∠ A=∠ BPD，‎ ‎∵△ PCD 是等边三角形，‎ ‎∴∠ PCD=∠ CPD=60°，‎ ‎∴∠ PCD=∠ A+∠ APC=6°0 ，‎ ‎∴∠ APC+∠ BPD=6°0 ，‎ ‎∴∠ APB=∠ APC+∠ CPD+∠ BPD=12°0 ．‎ 故选： B．‎ ‎7．（ 3 分）如图，在 Rt△ ABC中，∠ ACB=90°， CD 是斜边 AB 上的高，下列线段的比值等于 cosA的值的有 ‎（ ）个 ‎（ 1） （ 2） （ 3） （ 4） ．‎ A． 1 B． 2 C． 3 D． 4‎ ‎【解答】解：∵在 Rt△ ABC 中，∠ ACB=9°0 ， CD 是斜边 AB 上的高，‎ ‎∴∠ A+∠ ACD=9°0 ，∠ ACD+∠ BCD=9°0 ，‎ ‎∴∠ A=∠ BCD，‎ ‎∴ cosA= = = ，‎ 故（ 1），（ 2），（4）正确． 故选： C．‎ ‎8．（ 3 分）已知二次函数 y=ax ‎2+bx+c（ a≠ 0）的图象如图所示，且关于 x 的一元二次方程 ax2+bx+c﹣m=0‎ 没有实数根，则下列结论：① b2﹣ 4ac＞ 0；② ac＜ 0；③ m＞ 2，其中正确结论的个数是（ ）‎ A． 0 B． 1 C． 2 D． 3‎ ‎【解答】解：由二次函数 y=ax2+bx+c（ a≠ 0）的图象与 x 轴两个交点，可得 b2﹣4ac＞ 0，故①正确， 由二次函数 y=ax2+bx+c（ a≠0）的图象可知 a＜ 0， c＞ 0，则 ac＜ 0，故②正确，‎ 由二次函数 y=ax2+bx+c（ a≠0）的图象可知该函数有最大值，最大值是 y=2，‎ ‎∵关于 x 的一元二次方程 ax2+bx+c﹣ m=0 没有实数根，则 m＞ 2，故③正确， 故选： D．‎ 二、填空题（共 6 小题，每小题 3 分，满分 18 分）‎ ‎9．（ 3 分）小明和小红在阳光下行走，小明身高 1.75 米，他的影长 2.0 米，小红比小明矮 7 厘米，此刻小 红的影长是 1.92 米．‎ ‎【解答】解：根据题意知，小红的身高为 175﹣ 7=168（厘米）， 设小红的影长为 x 厘米 则 = ，‎ 解得： x=192，‎ ‎∴小红的影长为 1.92 米，‎ 故答案为： 1.92．‎ ‎10 ．（ 3 分）若 =2，则 = 2 ．‎ ‎【解答】解：两边都乘（ x﹣ y），得 x=2x﹣ 2y，‎ 两边都减 x，都加 2y，‎ 得 ‎2y=x， 两边都除以 y，得 ‎=2， 故答案为： 2．‎ ‎=8 ．‎ ‎11 ．（ 3 分）某校去年对实验器材的投资为 2 万元，预计今明两年的投资总额为 8 万元，若设该校这两年 在实验器材投资上的平均增长率为 x，则可列方程： 2（ 1+x） +2（ 1+x） 2‎ ‎【解答】解：∵去年对实验器材的投资为 2 万元，该校这两年在实验器材投资上的平均增长率为 x，‎ ‎∴今年的投资总额为 2（ 1+x）；明年的投资总额为 2（ 1+x） 2；‎ ‎∵预计今明两年的投资总额为 8 万元，‎ ‎=8．‎ ‎∴ 2（ 1+x） +2（ 1+x） 2‎ ‎12 ．（ 3 分）如图，小明晚上由路灯 A 下的 B 处走到 C 处时，测得影长 CD 的长为 1m ，从 C处继续往前走 ‎3m 达到 E 处时，测得影子 EF 的长为 2m ，已知小明的身高时 1.5m，那么路灯 A 的高度 AB 等于 6 m．‎ ‎【解答】解：如图，‎ ‎∵ = ，‎ 当小明在 CG处时， Rt△ DCG∽ Rt△ DBA，即 = ， 当小明在 EH处时， Rt△ FEH∽ Rt△ FBA，即 = = ，‎ ‎∴ = ，‎ ‎∵ CG=EH=1.5米， CD=1米， CE=3米， EF=2米， 设 AB=x， BC=y，‎ ‎∴ = ， 解得 y=3，‎ ‎∵ = ，‎ ‎∴ = ， 解得 x=6 米，‎ 即路灯 A 的高度 AB=6 米． 故答案为： 6．‎ ‎13 ．（ 3 分）下表是二次函数 y=ax2+bx+c 的自变量 x 和因变量 y 的对应值表：‎ x ﹣ 3 ﹣ 2 ﹣ 1 0 1 2 3‎ y 12 5 0 ﹣ 3 ﹣ 4 ﹣ 3 0‎ 若点 A（ x1， y1）、 B（ x2， y2）都在这个二次函数的图象上，且 3＜ x1＜ x2，则 y1、 y2 的大小关系是 y1 ＜‎ y2，．（填写 “＜ ”， “＞ ”或 “=）”‎ ‎【解答】解：∵当﹣ 3＜ x＜ 1 时，﹣ 4＜ y＜ 12， y 随 x 增大而减小；当 1＜ x＜ 3 时，﹣ 4＜ y＜ 0， y 随 x 增 大而增大，‎ ‎∴当 3＜ x1＜ x2 时， y1＜ y2， 故答案为：＜‎ ‎14 ．（ 3 分）如图， 10 个边长为 1 的正方形摆放在平面直角坐标系中，经过 A（ 1， 0）点的一条直线 1 将 这 10 个正方形分成面积相等的两部分，则该直线的解析式为 y= x﹣ ．‎ ‎【解答】解：将由图中 1 补到 2 的位置，‎ ‎∵ 10 个正方形的面积之和是 10，‎ ‎∴梯形 ABCD的面积只要等于 5 即可，‎ ‎∴设 BC=4﹣ x，则 [ （ 4﹣ x）+3] × 3÷ 2=5， 解得， x= ，‎ ‎∴点 B 的坐标为（ ，3），‎ 设过点 A 和点 B 的直线的解析式为 y=kx+b，‎ ‎，‎ 解得， ，‎ 即过点 A 和点 B 的直线的解析式为 y= ， 故答案为： y= ．‎ 三、解答题（共 10 小题，满分 78 分）‎