2020九年级数学上册 第4章 相似三角形 4 5页

‎4.6　相似多边形(见B本45页)‎ A　练就好基础　基础达标 ‎1．下列多边形一定相似的是(　D　)‎ A．两个平行四边形　　　 B．两个菱形 ‎ C．两个矩形 D．两个正六边形 ‎2．如果两个相似多边形的面积比为4：9，那么它们的周长比为(　B　)‎ A．4∶9 B．2∶3 C.∶ D．16∶81‎ ‎3．小红的妈妈做了一个矩形枕套(长、宽不等)，又在枕套四周镶上了相同宽度的花边，如图所示，关于两个矩形，下列说法中正确的是(　C　)‎ A．两个矩形相似 B．两个矩形不一定相似 C．两个矩形一定不相似 D．无法判断是否相似 第3题图 ‎　　第4题图 ‎4．如图所示，在长为8 cm、宽为4 cm的矩形中，截去一个矩形，使得留下的矩形(阴影部分)与原矩形相似，则留下矩形的面积是(　C　) ‎ A．2 cm2 B．4 cm2 C．8 cm2 D．16 cm2‎ ‎5．已知五边形ABCDE与五边形A′B′C′D′E′相似，相似比为，五边形ABCDE的周长为27 cm，则五边形A′B′C′D′E′的周长是__45__ cm .‎ ‎6．两个相似多边形的一组对应边分别为3 cm和4.5 cm，如果它们的面积之和为130 cm2，那么较小的多边形的面积是__40__cm2.‎ ‎7．如图所示，六边形ABCDEF∽六边形GHIJKL，相似比为2∶1，则下列结论正确的序号是__②③__．‎ ‎①∠B＝2∠K；‎ ‎②BC＝2HI；‎ ‎③六边形ABCDEF的周长是六边形GHIJKL的周长的2倍；‎ ‎④S六边形ABCDEF＝2S六边形GHIJKL.‎ 第7题图 第8题图 ‎8．如图所示，把矩形ABCD对折，折痕为MN，矩形DMNC与矩形ABCD相似，已知AB＝4.‎ ‎(1)求AD的长；‎ ‎(2)求矩形DMNC与矩形ABCD的相似比．‎ 解：(1)由已知，得MN＝AB，MD＝AD＝BC.‎ ‎∵矩形DMNC与矩形ABCD相似，‎ ‎∴＝.‎ ‎∵MN＝AB，DM＝AD BC＝AD，∴AD2＝AB2.‎ 由AB＝4得，AD＝4.‎ ‎(2)矩形DMNC与矩形ABCD的相似比为＝.‎ B　更上一层楼　能力提升 ‎9．如图所示，菱形ABCD的对角线AC＝4 cm，把它沿着对角线AC方向平移1 cm得到菱形EFGH，则图中阴影部分图形的面积与四边形EMCN的面积之比为(　C　)‎ A．4∶3　 B．3∶2　 C．14∶9　 D．17∶9‎ 第9题图 ‎10．如图所示，一般书本的纸张是在原纸张上进行多次对开得到的．矩形ABCD沿EF对开后，再把矩形EFCD沿MN对开，依此类推．若各种开本的矩形都相似，那么AB∶AD＝____．‎ 第10题图 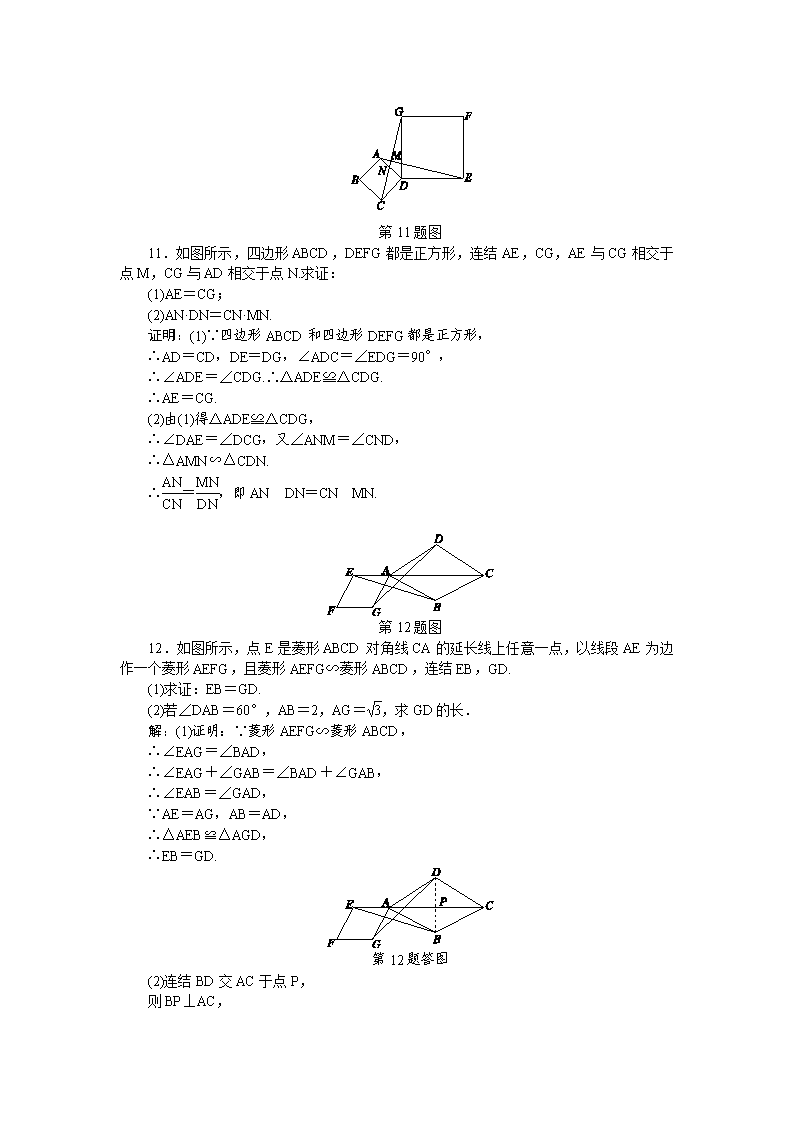第11题图 ‎11．如图所示，四边形ABCD，DEFG都是正方形，连结AE，CG，AE与CG相交于点M，CG与AD相交于点N.求证：‎ ‎(1)AE＝CG；‎ ‎(2)AN·DN＝CN·MN.‎ 证明：(1)∵四边形ABCD和四边形DEFG都是正方形，‎ ‎∴AD＝CD，DE＝DG，∠ADC＝∠EDG＝90°，‎ ‎∴∠ADE＝∠CDG.∴△ADE≌△CDG.‎ ‎∴AE＝CG.‎ ‎(2)由(1)得△ADE≌△CDG，‎ ‎∴∠DAE＝∠DCG，又∠ANM＝∠CND，‎ ‎∴△AMN∽△CDN.‎ ‎∴＝，即ANDN＝CNMN.‎ 第12题图 ‎12．如图所示，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且菱形AEFG∽菱形ABCD，连结EB，GD.‎ ‎(1)求证：EB＝GD.‎ ‎(2)若∠DAB＝60°，AB＝2，AG＝，求GD的长．‎ 解：(1)证明：∵菱形AEFG∽菱形ABCD，‎ ‎∴∠EAG＝∠BAD，‎ ‎∴∠EAG＋∠GAB＝∠BAD＋∠GAB，‎ ‎∴∠EAB＝∠GAD，‎ ‎∵AE＝AG，AB＝AD，‎ ‎∴△AEB≌△AGD，‎ ‎∴EB＝GD.‎ 第12题答图 ‎(2)连结BD交AC于点P，‎ 则BP⊥AC，‎ ‎∵∠DAB＝60°，‎ ‎∴∠PAB＝30°，‎ ‎∴BP＝AB＝1，‎ AP＝＝，AE＝AG＝，‎ ‎∴EP＝2，‎ ‎∴EB＝＝＝，‎ ‎∴GD＝.‎ C　开拓新思路　拓展创新 第13题图 ‎13．南宁中考有3个正方形如图所示放置，阴影部分的面积依次记为S1，S2，则S1∶S2等于(　D　)‎ A．1∶ B．1∶2 C．2∶3 D．4∶9‎ ‎14．如图所示，在矩形ABCD中，AD＝3，AB＝1.‎ ‎(1)若EF把矩形分成两个小的矩形，其中矩形ABEF与矩形ABCD相似．求AF∶AD的值；‎ ‎(2)若在矩形ABCD内不重叠地放两个长是宽的3倍的小长方形，且每个小长方形的每条边与矩形ABCD的边平行，求这两个小长方形周长和的最大值．‎ 第14题图 解：(1)设AF＝x, ∵矩形ABEF与矩形ABCD相似，AD＝3，AB＝1, ∴AB∶AD＝AF∶AB，即1∶3＝x∶1，解得x＝.‎ ‎∴AF∶AD＝∶3＝1∶9.‎ ‎(2)两个小矩形的放置情况有如下几种：‎ ‎①两个小矩形都“竖放”，如答图(a)，在这种放法下，周长和最大的两个小矩形，边长分别为1和， 故此时周长和的最大值为.‎ 第14题答图 ‎②两个小矩形都“横放”，如答图(b)及答图(c)所示，这时两个小矩形的周长和的最大值是2(a＋3a)＋2[1－a＋3(1－a)]＝8.‎ ‎③两个小矩形一个“横放”，一个“竖放”，如答图(d)所示，这时两个小矩形的周长和为2(a＋3a)＋2＝8＋，‎ 因为0＜3a≤1，‎ 即0＜a≤，故当a＝时，此时两个小矩形的周长和最大值为.综上，可知所求的最大值为.‎