北师大版数学九年级上册同步练习课件-第4章 图形的相似-第4章 7相似三角形的性质 16页

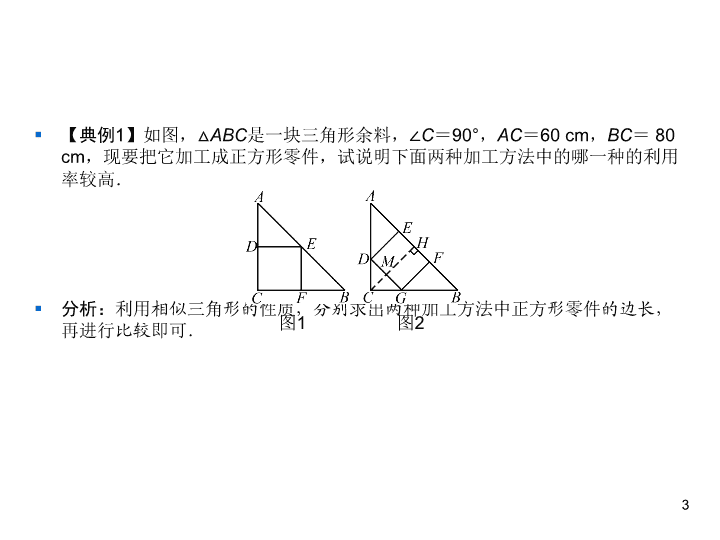
第四章　图形的相似 7　相似三角形的性质(一课时) § 知识点1　相似三角形的性质 § (1)相似三角形对应角相等，对应边成比例，且对应边之比等于相似比． § (2)相似三角形对应高的比，对应角平分线的比，对应中线的比都等于相 似比． § (3)相似三角形的周长比等于相似比，面积比等于相似比的平方． § (4)相似三角形性质的作用： § ①证明角相等，线段成比例； § ②证明线段的平方比； § ③解决相似三角形的有关运算． 2 § 【典例1】如图，△ABC是一块三角形余料，∠C＝90°，AC＝60 cm，BC＝ 80 cm，现要把它加工成正方形零件，试说明下面两种加工方法中的哪一种的利 用率较高． § 分析：利用相似三角形的性质，分别求出两种加工方法中正方形零件的边长， 再进行比较即可． 3 图1　　　　　图2 4 5 § 知识点2　相似多边形的性质 § 相似多边形具有对应角相等、对应线段(包括边、中线、高线、角平分 线等)之比等于相似比，对应面积之比等于相似比的平方等性质． § 【典例2】已知甲、乙两个多边形相似，其相似比为2∶ 3. § (1)若多边形甲的周长为24，则多边形乙的周长为________； § (2)若两个多边形的面积之和为117，则多边形甲的面积为________． 6 § 答案：(1)36　(2)36 7 § 1．【重庆中考】已知△ABC∽△DEF，且相似比为1∶ 2，则 △ABC与△DEF的面积比为(　　) § A．1∶ 4 B．4∶ 1 § C．1∶ 2 D．2∶ 1 § 2．两个相似三角形对应角平分线之比为4∶ 9，那么它们的面积 之比为(　　) § A．2∶ 3 B．4∶ 9 § C．8∶ 27 D．16∶ 81 8 A 　 D 　 § 3．【2018·贵州铜仁中考】已知 △ABC∽△DEF，相似比为2，且△ABC的 面积为16，则△DEF的面积为(　　) § A．32 B．8 § C．4 D．16 § 4．已知两个相似多边形的面积比是9∶ 16， 其中较小多边形的周长为36 cm，则较大多 边形的周长为(　　) § A．48 cm B．54 cm § C．56 cm D．64 cm 9 C 　 A 　 10 C 　 11 B 　 § 7．如图，已知E为□ABCD的AD边上一点，且AE∶ ED＝1∶ 2，若△AEF的周 长为6，则△CBF的周长为__________. § 8．【北京中考】如图，在△ABC中，M、N分别为AC、BC的中点．若S△C M N ＝1，则S四边形ABNM＝_________. 12 18　 3　 § 9．如图，△ABC中，AC＝6，AB＝4，点D与点A在直线BC的同侧，且∠ACD＝∠ABC，CD＝2，点 E是线段BC延长线上的动点，当△DCE和△ABC相似时，线段CE的长为___________. § 10．如图，若△ADE∽△ACB，AB＝8，AE＝4，DE＝3，则BC＝_________. 13 6　 14 § 12．已知两个相似多边形的一对对应边的边长分别是15 cm和12 cm. § (1)若它们的周长相差24 cm，求这两个多边形的周长； § (2)若它们的面积相差270 cm2，求这两个多边形的面积． § 解：(1)设较大多边形的周长为x cm.∵两个相似多边形的一对对应边分别是15 cm和12 cm，∴两个相似多边形的相似比是15∶12＝5∶4.又∵相似多边形的周 长的比等于相似比，∴x∶(x－24)＝5∶4，解得x＝120.则较小多边形的周长为 120－24＝96( cm)，故这两个多边形的周长分别为120 cm、96 cm. § (2)设较大多边形的面积为a cm2.由题意，得a∶(a－270)＝25∶16，解得a＝ 750.则较小多边形的面积为750－270＝480( cm2)，故这两个多边形的面积分别 为750 cm2、480 cm2. 15 § 13．某施工地在道路拓宽施工时遇到这样一个问题，马路旁边 原有一个面积为100平方米，周长为80米的三角形绿化地，由 于马路拓宽绿地被消去了一个角，即△ADE，变成了一个梯形 BCED，原绿化地一边AB的长由原来的30米缩短成BD长18米， 求被消去部分的面积有多大？它的周长是多少？ 16