2020届新苏科版九年级上期中考试数学试题（苏教版九年级数学上册期中考试测试题） 8页

苏教版九年级数学上册期中考试测试题 一、选择题(本大题共 10 小题，每小题 3 分，共 30 分．在每小题所给出的四个选项中， 只有一项是正确的，请把答案直接写在答卷上相应的位置处．．．．．．．．．) 1．下列函数关系中，y 是 x 的二次函数的是 ………………………………… ( ) A．y = 2x + 3 B．y = 1x C．y = x2 − 1 D．y = 1 x2 + 1 2．如图，已知⊙O 是正方形 ABCD 的外接圆，点 E 是︵ AD上任意一点，则∠BEC 的度数为 …………………………………………………………………………………… ( ) A．30° B. 45° C. 60° D. 90° 3．二次函数 y = −3x2 − 6x + 5 的图象的顶点坐标是 …………………………… ( ) A．(−1，8) B．(1，8) C．(−1，2) D．(1，−4) 4．已知圆锥的底面半径为 6cm，高为 8cm，则这个圆锥的母线长为 ……… ( ) A．12cm B．10cm C．8cm D．6cm 5．把抛物线 y = −x2 向左平移 1 个单位，然后向上平移 3 个单位，则平移后抛物线的解析 式为 …………………………………………………………………………… ( ) A．y = −(x − 1)2 − 3 B．y = −(x + 1)2 − 3 C．y = −(x − 1)2 + 3 D．y = −(x + 1)2 + 3 6．如图，两个同心圆的半径分别为 4cm 和 5cm，大圆的一条弦 AB 与小圆相切，则弦 AB 的长为 ………………………………………………………………………… ( ) A．3cm B．4cm C．6cm D．8cm E DA B C O 第 2 题图 第 6 题图 第 9 题图 7．已知点 A 在半径为 r 的⊙O 内，点 A 与点 O 的距离为 6，则 r 的取值范围是 ( ) A．r > 6 B．r ≥ 6 C．r < 6 D．r ≤ 6 8．已知二次函数 y = −x2 − 2x + k 的图象经过点 A(1，y1)，B( 2 ，y2)，C(−2，y3)，则下 列结论正确的是 ……………………………………………………………… ( ) A．y1 < y2 < y3 B．y2 < y1 < y3 C．y3 < y1 < y2 D．y1 < y3 < y2 9．已知二次函数 y = ax2 + bx + c (a ≠ 0)的图象如图所示，在下列五个结论中： ①2a − b < 0；②abc < 0；③a + b + c < 0；④a − b + c > 0；⑤4a + 2b + c > 0．其中错误 的有 …………………………………………………………………………… ( ) A．1 个 B．2 个 C．3 个 D．4 个 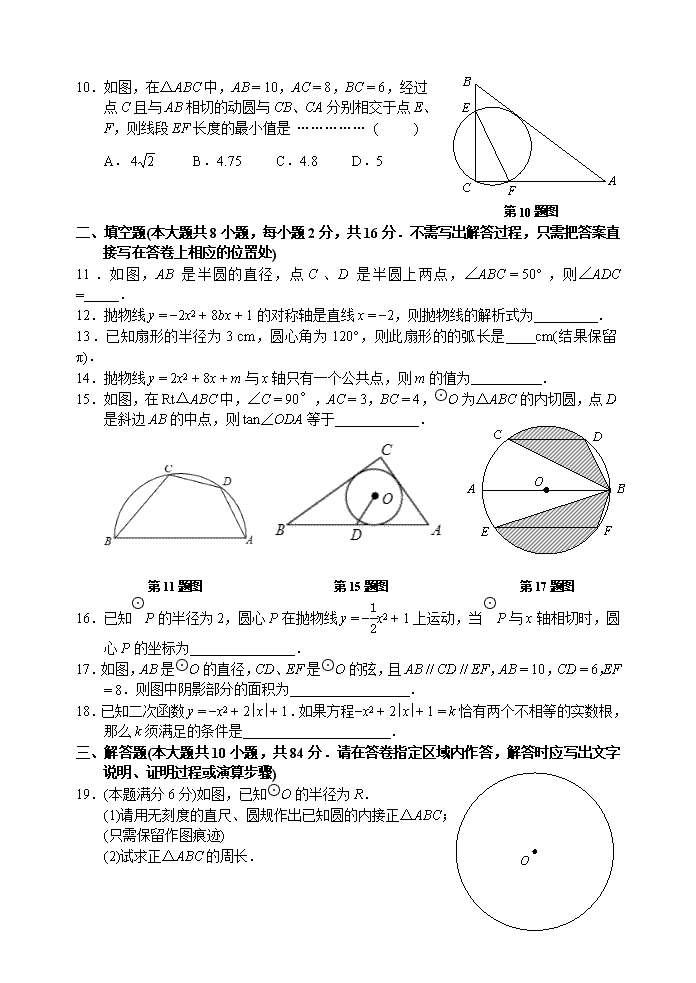10．如图，在△ABC 中，AB = 10，AC = 8，BC = 6，经过 点 C 且与 AB 相切的动圆与 CB、CA 分别相交于点 E、 F，则线段 EF 长度的最小值是 …………… ( ) A． 24 B．4.75 C．4.8 D．5 第 10 题图 二、填空题(本大题共 8 小题，每小题 2 分，共 16 分．不需写出解答过程，只需把答案直 接写在答卷上相应的位置处．．．．．．．．．) 11．如图，AB 是半圆的直径，点 C、D 是半圆上两点，∠ABC = 50°，则∠ADC = ． 12．抛物线 y = −2x2 + 8bx + 1 的对称轴是直线 x = −2，则抛物线的解析式为 ． 13．已知扇形的半径为 3 cm，圆心角为 120°，则此扇形的的弧长是 cm(结果保留π)． 14．抛物线 y = 2x2 + 8x + m 与 x 轴只有一个公共点，则 m 的值为 ． 15．如图，在 Rt△ABC 中，∠C = 90°，AC = 3，BC = 4，⊙O 为△ABC 的内切圆，点 D 是斜边 AB 的中点，则 tan∠ODA 等于 ． 第 11 题图 第 15 题图 第 17 题图 16．已知⊙P 的半径为 2，圆心 P 在抛物线 y = −1 2x2 + 1 上运动，当⊙P 与 x 轴相切时，圆 心 P 的坐标为 ． 17．如图，AB 是⊙O 的直径，CD、EF 是⊙O 的弦，且 AB // CD // EF，AB = 10，CD = 6， EF = 8．则图中阴影部分的面积为 ． 18．已知二次函数 y = −x2 + 2|x|+ 1．如果方程−x2 + 2|x|+ 1 = k 恰有两个不相等的实数根， 那么 k 须满足的条件是 ． 三、解答题(本大题共 10 小题，共 84 分．请在答卷指定区域内作答．．．．．．．．．，解答时应写出文字 说明、证明过程或演算步骤) 19．(本题满分 6 分)如图，已知⊙O 的半径为 R． (1)请用无刻度的直尺、圆规作出已知圆的内接正△ABC； (只需保留作图痕迹) (2)试求正△ABC 的周长． 第 19 题图 C A B E F A BO C D E F O 20．(本题满分 8 分)如图，已知二次函数 y = ax2 − 4x + c 的图象经过点 A 和点 B． (1)求该二次函数的表达式； (2)写出该抛物线的对称轴及顶点坐标； (3)若点 P(m，m)在该函数图象上，求 m 的值． 第 20 题图 21．(本题满分 7 分)如图，AB 为⊙O 的直径，点 C 在⊙O 上，延长 BC 至点 D，使 DC = CB． 延长 DA 与⊙O 的另一个交点为 E，连结 AC，CE． (1)求证：∠B =∠D；(2)若⊙O 的半径为 2，AC = 2，求 CE 的长． A BCD E O 第 21 题图 22．(本题满分 6 分)如图，已知 AB 是⊙O 的弦，OB = 2，∠B = 30°，点 C 是弦 AB 上任意 一点(不与点 A、B 重合)，连接 CO 并延长 CO 交⊙O 于点 D，连接 AD． (1)求弦 AB 的长；(2)当∠D = 20°时，求∠BOD 的度数． O A BC D 第 22 题图 23．(本题满分 8 分)如图，已知抛物 y = x2 + bx + c 与 x 轴交于点 A、B，AB = 2，与 y 轴交 于点 C，对称轴为直线 x = 2． (1)求抛物线的函数表述式； (2)设 P 为对称轴上一动点，求△APC 周长的最小值； 第 23 题图 24．(本题满分 8 分)如图，AB 是⊙O 的直径，BC 为⊙O 的切线，D 为⊙O 上的一点， CD = CB，延长 CD 交 BA 的延长线于点 E． (1)求证：CD 为⊙O 的切线；(2)若 OF⊥BD 于点 F，且 OF = 1，∠ABD = 30°，求图 中阴影部分的面积．(结果保留π) 第 24 题图 25．(本题满分 9 分)某公司在固定线路上运输，拟用运营指数 Q 量化考核司机的工作业绩． Q = W + 100，而 W 的大小与运输次数 n 及平均速度 x (km/h)有关(不考虑其他因素)， W 由两部分的和组成：一部分与 x 的平方成正比，另一部分与 x 的 n 倍成正比．试行 中得到了表中的数据． (1)用含 x 和 n 的式子表示 Q； (2)若 n = 3，要使 Q 最大，确定 x 的值； (3)设 n = 2，x = 40，能否在 n 增加 m% (m > 0)同时 x 减少 m%的情况下，而 Q 的值仍为 420，若能，求出 m 的值；若不 能，请说明理由． 次数 n 2 1 速度 x 40 60 指数 Q 420 100 26．(本题满分 10 分)已知抛物线的顶点为(0，4)且与 x 轴交于(−2，0)，(2，0)． (1)直接写出抛物线解析式； (2)如图，将抛物线向右平移 k 个单位，设平移后抛物线的顶点为 D，与 x 轴的交点为 A、B，与原抛物线的交点为 P． ①当直线 OD 与以 AB 为直径的圆相切于点 E 时，求此时 k 的值； ②是否存在这样的 k 的值，使得点 O、P、D 三点恰好在同一直线上？若存在，求出 k 的值；若不存在，请说明理由． 第 26 题图 备用图 27．(本题满分 12 分)如图，在平面直角坐标系中，四边形 OABC 是边长为 2 的正方形，二 次函数 y = ax2 + bx + c 的图象经过点 A，B，与 x 轴分别交于点 E，F，且点 E 的坐标( 3 2 ， 0)，以 OC 为直径作半圆，圆心为 D． (1)求二次函数的解析式； (2)求证：直线 BE 是⊙D 的切线； (3)若直线 BE 与抛物线的对称轴交点为 P，M 是线段 CB 上的一个动点(点 M 与点 B， C 不重合），过点 M 作 MN // BE 交 x 轴于点 N，连结 PM，PN，设 CM 的长为 t，△PMN 的面积为 S，求 S 与 t 的函数关系式，并写出自变量 t 的取值范围．问 S 是否存在最大 值？若存在，求出最大值；若不存在，请说明理由． 第 27 题图 备用图 28．(本题满分 10 分)在半径为 2 的扇形 AOB 中，∠AOB = 90°，P 是 OA 延长线上一点， 过线段 OP 的中点 H 作 OP 的垂线交弧 AB 于点 C，射线 PC 交弧 AB 于点 D，联结 OD． (1)如图，当︵ AC = ︵ CD时，求弦 CD 的长； (2)如图，当点 C 在︵ AD上时，设 PA = x，CD = y，求 y 与 x 的函数关系式，并写出 x 的取值范围； AO B D C H P AO B 第 28 题图 备用图