2019-2020学年福建漳州九年级上数学期中试卷 5页

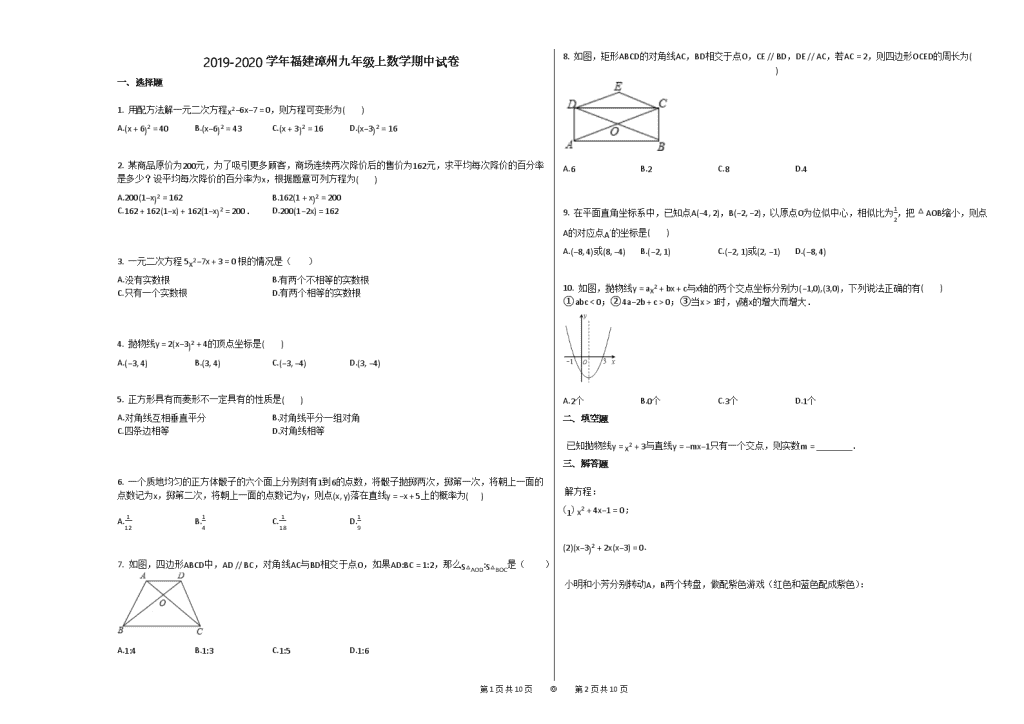
‎2019-2020学年福建漳州九年级上数学期中试卷 一、选择题 ‎ ‎ ‎1. 用配方法解一元二次方程x‎2‎‎−6x−7=0‎，则方程可变形为(        ) ‎ A.‎(x+6‎)‎‎2‎=40‎ B.‎(x−6‎)‎‎2‎=43‎ C.‎(x+3‎)‎‎2‎=16‎ D.‎‎(x−3‎)‎‎2‎=16‎ ‎ ‎ ‎2. 某商品原价为‎200‎元，为了吸引更多顾客，商场连续两次降价后的售价为‎162‎元，求平均每次降价的百分率是多少？设平均每次降价的百分率为x，根据题意可列方程为‎(‎        ‎)‎ ‎ A.‎200(1−x‎)‎‎2‎=162‎ B.‎162(1+x‎)‎‎2‎=200‎ C.‎162+162(1−x)+162(1−x‎)‎‎2‎=200‎． D.‎200(1−2x)=162‎ ‎ ‎ ‎ ‎3. 一元二次方程 ‎5x‎2‎−7x+3=0‎ 根的情况是（        ） ‎ A.没有实数根 B.有两个不相等的实数根 C.只有一个实数根 D.有两个相等的实数根 ‎ ‎ ‎ ‎4. 抛物线y=2(x−3‎)‎‎2‎+4‎的顶点坐标是(        ) ‎ A.‎(−3, 4)‎ B.‎(3, 4)‎ C.‎(−3, −4)‎ D.‎‎(3, −4)‎ ‎ ‎ ‎5. 正方形具有而菱形不一定具有的性质是‎(‎        ‎)‎ ‎ A.对角线互相垂直平分 B.对角线平分一组对角 C.四条边相等 D.对角线相等 ‎ ‎ ‎ ‎6. 一个质地均匀的正方体骰子的六个面上分别刻有‎1‎到‎6‎的点数，将骰子抛掷两次，掷第一次，将朝上一面的点数记为x，掷第二次，将朝上一面的点数记为y，则点‎(x, y)‎落在直线y=−x+5‎上的概率为‎(‎      ‎)‎ ‎ A.‎1‎‎12‎ B.‎1‎‎4‎ C.‎1‎‎18‎ D.‎‎1‎‎9‎ ‎ ‎ ‎7. 如图，四边形ABCD中，AD // BC，对角线AC与BD相交于点O，如果AD:BC‎=‎‎1:2‎，那么S‎△AOD‎:‎S‎△BOC是（         ） ‎ A.‎1:4‎ B.‎1:3‎ C.‎1:5‎ D.‎‎1:6‎ ‎ ‎ ‎8. 如图，矩形ABCD的对角线AC，BD相交于点O，CE // BD，DE // AC，若AC=2‎，则四边形OCED的周长为‎(‎        ‎)‎ ‎ A.‎6‎ B.‎2‎ C.‎8‎ D.‎‎4‎ ‎ ‎ ‎9. 在平面直角坐标系中，已知点A(−4, 2)‎，B(−2, −2)‎，以原点O为位似中心，相似比为‎1‎‎2‎，把‎△AOB缩小，则点A的对应点A‎′‎的坐标是(        ) ‎ A.‎(−8, 4)‎或‎(8, −4)‎ B.‎(−2, 1)‎ C.‎(−2, 1)‎或‎(2, −1)‎ D.‎‎(−8, 4)‎ ‎ ‎ ‎10. 如图，抛物线y=ax‎2‎+bx+c与x轴的两个交点坐标分别为‎(−1,0),(3,0)‎，下列说法正确的有(        ) ①abc<0‎；②‎4a−2b+c>0‎；③当x>1‎时，y随x的增大而增大． ‎ A.‎2‎个 B.‎0‎个 C.‎3‎个 D.‎1‎个 二、填空题 ‎ ‎ ‎ 已知抛物线y=x‎2‎+3‎与直线y=−mx−1‎只有一个交点，则实数m‎=‎________． ‎ 三、解答题 ‎ ‎ ‎ 解方程： ‎ ‎1‎‎ x‎2‎‎+4x−1=0‎ ;‎ ‎ ‎ ‎(2)(x−3‎)‎‎2‎+2x(x−3)=0‎‎.‎ ‎ ‎ ‎ 小明和小芳分别转动A，B两个转盘，做配紫色游戏（红色和蓝色配成紫色）： ‎ 第9页 共10页 ◎ 第10页 共10页 ‎ ‎ ‎(1)‎利用列表或树状图的方法表示此游戏所有可能出现的结果；‎ ‎ ‎ ‎(2)‎若配成紫色，则小明胜，否则小芳胜，此游戏的规则对小明、小芳公平吗？试说明理由．‎ ‎ ‎ ‎ 如图，四边形ABCD中，AD // BC，AC平分‎∠BAD，BD平分‎∠ABC，试判断四边形ABCD的形状并证明． ‎ ‎ ‎ ‎ 已知关于x的一元二次方程mx‎2‎−(m+2)x+2=0(m≠0)‎． ‎ ‎(1)‎求证：方程总有两个实数根；‎ ‎ ‎ ‎(2)‎若方程的两个实数根都是整数，求正整数m的值．‎ ‎ ‎ ‎ 如图，在矩形ABCD中，E、F分别是边BC、AB上的点，且 EF=ED,EF⊥ED. ‎ ‎(1)‎求证： ‎△DCE≅△EBF；‎ ‎ ‎ ‎(2)‎若 AB=3,BC=4‎ ，求AE的长.‎ ‎ ‎ ‎ 利用一面墙（墙的长度不限），另三边用‎60‎米长的篱笆围成矩形ABCD,设 AB=x 米，矩形ABCD的面积‎=‎y米‎​‎‎2‎. ‎ ‎1‎当 y=400‎ 时，求x的值；‎ ‎ ‎ ‎2‎求y与x的函数关系式，当x取何值时，y有最大值，并求这个最大值‎.‎ ‎ ‎ ‎ 如图，在正方形ABCD中，‎△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，BD与CF相交于点H． ‎ ‎1‎直接写出答案： ‎∠PBD=‎________度， DFBC‎=‎________;‎ ‎ ‎ ‎2‎求证：‎△DFP∼△BPH；‎ ‎ ‎ ‎3‎求证：PD‎2‎‎=‎PB⋅PH.‎ ‎ ‎ ‎ 我们知道，经过原点的抛物线的解析式可以是y=ax‎2‎+bx(a≠0)‎ ‎ ‎(1)‎对于这样的抛物线：当顶点坐标为‎(1, 1)‎时，a=‎________； 当顶点坐标为‎(m, m)‎，m≠0‎时，a与m之间的关系式是________；‎ ‎ ‎ ‎(2)‎继续探究，如果b≠0‎，且过原点的抛物线顶点在直线y=kx(k≠0)‎上，请用含k的代数式表示b；‎ ‎ ‎ ‎(3)‎现有一组过原点的抛物线，顶点A‎1‎，A‎2‎，‎⋯‎，A‎12‎在直线y=x上，横坐标依次为‎1‎，‎2‎，‎⋯‎，‎12‎，分别过每个顶点作x轴的垂线，垂足记为B‎1‎，B‎2‎，‎⋯‎，B‎12‎，以线段AnBn为边向右作正方形AnBnCnDn(n为正整数，且‎1≤n≤12‎)，若这组抛物线中有一条经过Dn，求所有满足条件的正方形边长．‎ 第9页 共10页 ◎ 第10页 共10页 参考答案与试题解析 ‎2019-2020学年福建漳州九年级上数学期中试卷 一、选择题 ‎1.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 解因末二什方似-配方法 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎2.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 由实较燥题元效出一元二次方程 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎3.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 根体判展式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎4.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次明数织性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎5.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 正方来的性稳 菱都资性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎6.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一次常数图按上点入适标特点 列表法三树状图州 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎7.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎8.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 矩来兴性质 菱形的来定与筒质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎9.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 位因梯换 坐标正测形性质 ‎【解析】‎ 此题暂无解析 第9页 共10页 ◎ 第10页 共10页 ‎【解答】‎ 此题暂无解答 ‎10.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次射数空象与话数流关系 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 二、填空题 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次明数织性质 根体判展式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 三、解答题 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 解一较燥次延程抗因式分解法 解因末二什方似-配方法 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 游水于平性 列表法三树状图州 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 全根三烛形做给质与判定 菱因顿判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 根体判展式 一元二表方病的解 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 勾体定展 全等三表形木判定 全等三来形的稳质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一元二都问程的迹用--临何图形面积问题 二次表数擦应用 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 相验极角家的锰质与判定 锐角三较函数严定义 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 第9页 共10页 ◎ 第10页 共10页 二次使如综合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 第9页 共10页 ◎ 第10页 共10页