2020年贵州省黔西南州中考数学试卷【含答案及详细解释】 15页

1 / 15 2020 年贵州省黔西南州中考数学试卷 一、选择题（本题 10 小题，每题 4 分，共 40 分） 1. 2的倒数是（ ） A.−2 B.2 C.− 1 2 D.1 2 2. 某市为做好“稳就业、保民生”工作，将新建保障性住房360000套，缓解中低收 入人群和新参加工作大学生的住房需求．把360000用科学记数法表示应是（ ） A.0.36 × 106 B.3.6 × 105 C.3.6 × 106 D.36 × 105 3. 如图，由6个相同的小正方体组合成一个立体图形，它的俯视图为（ ） A. B. C. D. 4. 下列运算正确的是（ ） A.푎3 + 푎2＝푎5 B.푎3 ÷ 푎＝푎3 C.푎2 ⋅ 푎3＝푎5 D.(푎2)4＝푎6 5. 某学校九年级1班九名同学参加定点投篮测试，每人投篮六次，投中的次数统计 如下：4，3，5，5，2，5，3，4，1，这组数据的中位数、众数分别为（ ） A.4，5 B.5，4 C.4，4 D.5，5 6. 如图，将一块三角板的直角顶点放在直尺的一边上，当∠2＝37∘时，∠1的度数为 （ ） A.37∘ B.43∘ C.53∘ D.54∘ 7. 如图，某停车场入口的栏杆퐴퐵，从水平位置绕点푂旋转到퐴′퐵′的位置，已知퐴푂的 长为4米．若栏杆的旋转角∠퐴푂퐴′＝훼，则栏杆퐴端升高的高度为（ ） A. 4 sin훼 米 B.4sin훼米 C. 4 cos훼 米 D.4cos훼米 8. 已知关于푥的一元二次方程(푚 − 1)푥2 + 2푥 + 1＝0有实数根，则푚的取值范围是 （ ） A.푚 < 2 B.푚 ≤ 2 C.푚 < 2且푚 ≠ 1 D.푚 ≤ 2且푚 ≠ 1 9. 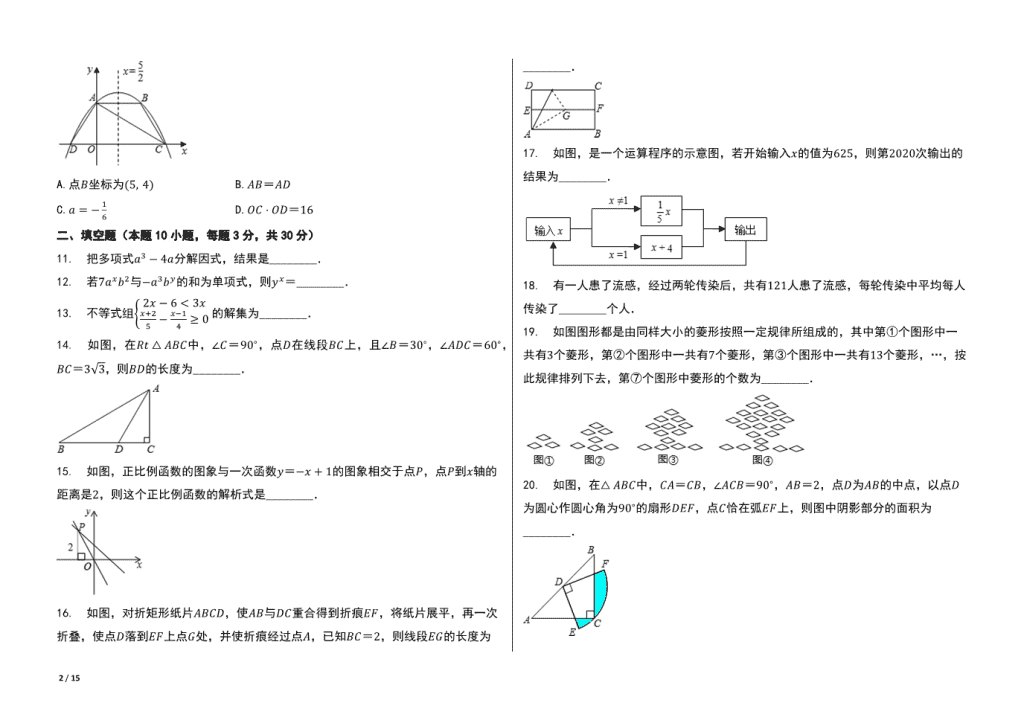如图，在菱形퐴퐵푂퐶中，퐴퐵＝2，∠퐴＝60∘，菱形的一个顶点퐶在反比例函数푦 = 푘 푥 (푘 ≠ 0)的图象上，则反比例函数的解析式为（ ） A.푦 = − 3√3 푥 B.푦 = − √3 푥 C.푦 = − 3 푥 D.푦 = √3 푥 10. 如图，抛物线푦＝푎푥2 + 푏푥 + 4交푦轴于点퐴，交过点퐴且平行于푥轴的直线于另一 点퐵，交푥轴于퐶，퐷两点（点퐶在点퐷右边），对称轴为直线푥 = 5 2 ，连接퐴퐶，퐴퐷， 퐵퐶．若点퐵关于直线퐴퐶的对称点恰好落在线段푂퐶上，下列结论中错误的是（ ） 2 / 15 A.点퐵坐标为(5,  4) B.퐴퐵＝퐴퐷 C.푎 = − 1 6 D.푂퐶 ⋅ 푂퐷＝16 二、填空题（本题 10 小题，每题 3 分，共 30 分） 11. 把多项式푎3 − 4푎分解因式，结果是________． 12. 若7푎푥푏2与−푎3푏푦的和为单项式，则푦푥＝________． 13. 不等式组{ 2푥 − 6 < 3푥 푥+2 5 − 푥−1 4 ≥ 0 的解集为________． 14. 如图，在푅푡 △ 퐴퐵퐶中，∠퐶＝90∘，点퐷在线段퐵퐶上，且∠퐵＝30∘，∠퐴퐷퐶＝60∘， 퐵퐶＝3√3，则퐵퐷的长度为________． 15. 如图，正比例函数的图象与一次函数푦＝−푥 + 1的图象相交于点푃，点푃到푥轴的 距离是2，则这个正比例函数的解析式是________． 16. 如图，对折矩形纸片퐴퐵퐶퐷，使퐴퐵与퐷퐶重合得到折痕퐸퐹，将纸片展平，再一次 折叠，使点퐷落到퐸퐹上点퐺处，并使折痕经过点퐴，已知퐵퐶＝2，则线段퐸퐺的长度为 ________． 17. 如图，是一个运算程序的示意图，若开始输入푥的值为625，则第2020次输出的 结果为________． 18. 有一人患了流感，经过两轮传染后，共有121人患了流感，每轮传染中平均每人 传染了________个人． 19. 如图图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一 共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，…，按 此规律排列下去，第⑦个图形中菱形的个数为________． 20. 如图，在△ 퐴퐵퐶中，퐶퐴＝퐶퐵，∠퐴퐶퐵＝90∘，퐴퐵＝2，点퐷为퐴퐵的中点，以点퐷 为圆心作圆心角为90∘的扇形퐷퐸퐹，点퐶恰在弧퐸퐹上，则图中阴影部分的面积为 ________． 3 / 15 三、解答题（本题 6 小题，共 80 分） 21. （1）计算(−2)2 − | − √2| − 2cos45∘ + (2020 − 휋)0； （2）先化简，再求值：( 2 푎+1 + 푎+2 푎2−1) ÷ 푎 푎−1 ，其中푎 = √5 − 1． 22. 规定：在平面内，如果一个图形绕一个定点旋转一定的角度훼(0∘ < 훼 ≤ 180∘)后 能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角度훼称为这个图形 的一个旋转角．例如：正方形绕着两条对角线的交点푂旋转90∘或180∘后，能与自身重 合（如图1），所以正方形是旋转对称图形，且有两个旋转角． 根据以上规定，回答问题： （1）下列图形是旋转对称图形，但不是中心对称图形的是________； 퐴．矩形 퐵．正五边形 퐶．菱形 퐷．正六边形 （2）下列图形中，是旋转对称图形，且有一个旋转角是60度的有：________（填序 号）； （3）下列三个命题：①中心对称图形是旋转对称图形；②等腰三角形是旋转对称图 形；③圆是旋转对称图形． 其中真命题的个数有________个； 퐴．0 퐵．1 퐶．2 4 / 15 퐷．3 （4）如图2的旋转对称图形由等腰直角三角形和圆构成，旋转角有45∘，90∘，135∘， 180∘，将图形补充完整． 23. 新学期，某校开设了“防疫宣传”“心理疏导”等课程．为了解学生对新开设课 程的掌握情况，从八年级学生中随机抽取了部分学生进行了一次综合测试．测试结果 分为四个等级：퐴级为优秀，퐵级为良好，퐶级为及格，퐷级为不及格．将测试结果绘 制了如图两幅不完整的统计图．根据统计图中的信息解答下列问题： （1）本次抽样测试的学生人数是________名； （2）扇形统计图中表示퐴级的扇形圆心角훼的度数是________，并把条形统计图补充 完整； （3）该校八年级共有学生500名，如果全部参加这次测试，估计优秀的人数为 ________； （4）某班有4名优秀的同学（分别记为퐸、퐹、퐺、퐻，其中퐸为小明），班主任要从中 随机选择两名同学进行经验分享．利用列表法或画树状图法，求小明被选中的概率． 24. 随着人们“节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行， 也给自行车商家带来商机.某自行车行经营的퐴型自行车去年销售总额为8万元.今年该 型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同，那么今年 的销售总额将比去年减少10%，求： (1)퐴型自行车去年每辆售价多少元？ (2)该车行今年计划新进一批퐴型车和新款퐵型车共60辆，且퐵型车的进货数量不超过퐴 型车数量的两倍.已知，퐴型车和퐵型车的进货价格分别为1500元和1800元，计划퐵型 车销售价格为2400元，应如何组织进货才能使这批自行车销售获利最多？ 25. 古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美 5 / 15 丽的圆．如图，线段퐴퐵是⊙ 푂的直径，延长퐴퐵至点퐶，使퐵퐶＝푂퐵，点퐸是线段푂퐵的 中点，퐷퐸 ⊥ 퐴퐵交⊙ 푂于点퐷，点푃是⊙ 푂上一动点（不与点퐴，퐵重合），连接퐶퐷， 푃퐸，푃퐶． （1）求证：퐶퐷是⊙ 푂的切线； （2）小明在研究的过程中发现푃퐸 푃퐶 是一个确定的值．回答这个确定的值是多少？并对 小明发现的结论加以证明． 26. 已知抛物线푦＝푎푥2 + 푏푥 + 6(푎 ≠ 0)交푥轴于点퐴(6,  0)和点퐵(−1,  0)，交푦轴于点퐶． （1）求抛物线的解析式和顶点坐标； （2）如图(1)，点푃是抛物线上位于直线퐴퐶上方的动点，过点푃分别作푥轴，푦轴的平 行线，交直线퐴퐶于点퐷，퐸，当푃퐷 + 푃퐸取最大值时，求点푃的坐标； （3）如图(2)，点푀为抛物线对称轴푙上一点，点푁为抛物线上一点，当直线퐴퐶垂直平 分△ 퐴푀푁的边푀푁时，求点푁的坐标． 6 / 15 参考答案与试题解析 2020 年贵州省黔西南州中考数学试卷 一、选择题（本题 10 小题，每题 4 分，共 40 分） 1.【答案】 D 【解答】 2的倒数是1 2 ， 2.【答案】 B 【解答】 360000＝3.6 × 105， 3.【答案】 【解答】 从上面看可得四个并排的正方形，如图所示： 故选：퐷． 4.【答案】 C 【解答】 퐴、푎3 + 푎2，不是同类项，无法合并，故此选项错误； 퐵、푎3 ÷ 푎＝푎2，故此选项错误； 퐶、푎2 ⋅ 푎3＝푎5，正确； 퐷、(푎2)4＝푎8，故此选项错误； 5.【答案】 A 【解答】 将数据从小到大排列为：1，2，3，3，4，4，5，5，5， 这组数据的中位数为4；众数为5． 6.【答案】 C 【解答】 ∵ 퐴퐵 // 퐶퐷，∠2＝37∘， ∴ ∠2＝∠3＝37∘， ∵ ∠1 + ∠3＝90∘， ∴ ∠1＝53∘， 7.【答案】 B 【解答】 过点퐴′作퐴′퐶 ⊥ 퐴퐵于点퐶， 由题意可知：퐴′푂＝퐴푂＝4， ∴ sin훼 = 퐴′퐶 퐴′푂 ， ∴ 퐴′퐶＝4sin훼， 8.【答案】 D 【解答】 ∵ 关于푥的一元二次方程(푚 − 1)푥2 − 2푥 + 1＝0有实数根， ∴ { 푚 − 1 ≠ 0 △=22 − 4 × 1 × (푚 − 1) ≥ 0 ， 解得：푚 ≤ 2且푚 ≠ 1． 9.【答案】 B 【解答】 7 / 15 ∵ 在菱形퐴퐵푂퐶中，∠퐴＝60∘，菱形边长为2， ∴ 푂퐶＝2，∠퐶푂퐵＝60∘， ∴ 点퐶的坐标为(−1, √3)， ∵ 顶点퐶在反比例函数푦 = 푘 푥 的图象上， ∴ √3 = 푘 −1 ，得푘 = −√3， 即푦 = − √3 푥 ， 10.【答案】 D 【解答】 ∵ 抛物线푦＝푎푥2 + 푏푥 + 4交푦轴于点퐴， ∴ 퐴(0,  4)， ∵ 对称轴为直线푥 = 5 2 ，퐴퐵 // 푥轴， ∴ 퐵(5,  4)． 故퐴无误； 如图，过点퐵作퐵퐸 ⊥ 푥轴于点퐸， 则퐵퐸＝4，퐴퐵＝5， ∵ 퐴퐵 // 푥轴， ∴ ∠퐵퐴퐶＝∠퐴퐶푂， ∵ 点퐵关于直线퐴퐶的对称点恰好落在线段푂퐶上， ∴ ∠퐴퐶푂＝∠퐴퐶퐵， ∴ ∠퐵퐴퐶＝∠퐴퐶퐵， ∴ 퐵퐶＝퐴퐵＝5， ∴ 在푅푡 △ 퐵퐶퐸中，由勾股定理得：퐸퐶＝3， ∴ 퐶(8,  0)， ∵ 对称轴为直线푥 = 5 2 ， ∴ 퐷(−3,  0) ∵ 在푅푡 △ 퐴퐷푂中，푂퐴＝4，푂퐷＝3， ∴ 퐴퐷＝5， ∴ 퐴퐵＝퐴퐷， 故퐵无误； 设푦＝푎푥2 + 푏푥 + 4＝푎(푥 + 3)(푥 − 8)， 将퐴(0,  4)代入得：4＝푎(0 + 3)(0 − 8)， ∴ 푎 = − 1 6 ， 故퐶无误； ∵ 푂퐶＝8，푂퐷＝3， ∴ 푂퐶 ⋅ 푂퐷＝24， 故퐷错误． 综上，错误的只有퐷． 二、填空题（本题 10 小题，每题 3 分，共 30 分） 11.【答案】 푎(푎 + 2)(푎 − 2) 【解答】 原式＝푎(푎2 − 4)＝푎(푎 + 2)(푎 − 2)． 12.【答案】 8 【解答】 8 / 15 ∵ 7푎푥푏2与−푎3푏푦的和为单项式， ∴ 7푎푥푏2与−푎3푏푦是同类项， ∴ 푥＝3，푦＝2， ∴ 푦푥＝23＝8． 13.【答案】 −6 < 푥 ≤ 13 【解答】 { 2푥 − 6 < 3푥 푥+2 5 − 푥−1 4 ≥ 0 ， 解①得：푥 > −6， 解②得：푥 ≤ 13， 不等式组的解集为：−6 < 푥 ≤ 13， 14.【答案】 2√3 【解答】 ∵ ∠퐶＝90∘，∠퐴퐷퐶＝60∘， ∴ ∠퐷퐴퐶＝30∘， ∴ 퐶퐷 = 1 2 퐴퐷， ∵ ∠퐵＝30∘，∠퐴퐷퐶＝60∘， ∴ ∠퐵퐴퐷＝30∘， ∴ 퐵퐷＝퐴퐷， ∴ 퐵퐷＝2퐶퐷， ∵ 퐵퐶＝3√3， ∴ 퐶퐷 + 2퐶퐷＝3√3， ∴ 퐶퐷 = √3， ∴ 퐷퐵＝2√3， 15.【答案】 푦＝−2푥 【解答】 ∵ 点푃到푥轴的距离为2， ∴ 点푃的纵坐标为2， ∵ 点푃在一次函数푦＝−푥 + 1上， ∴ 2＝−푥 + 1，得푥＝−1， ∴ 点跑的坐标为(−1,  2)， 设正比例函数解析式为푦＝푘푥， 则2＝−푘，得푘＝−2， ∴ 正比例函数解析式为푦＝−2푥， 16.【答案】 √3 【解答】 如图所示： 由题意可得：∠1＝∠2，퐴푁＝푀푁，∠푀퐺퐴＝90∘， 则푁퐺 = 1 2 퐴푀，故퐴푁＝푁퐺， ∴ ∠2＝∠4， ∵ 퐸퐹 // 퐴퐵， ∴ ∠4＝∠3， ∴ ∠1＝∠2＝∠3＝∠4 = 1 3 × 90∘＝30∘， ∵ 四边形퐴퐵퐶퐷是矩形，对折矩形纸片퐴퐵퐶퐷，使퐴퐵与퐷퐶重合得到折痕퐸퐹， ∴ 퐴퐸 = 1 2 퐴퐷 = 1 2 퐵퐶＝1， ∴ 퐴퐺＝2， ∴ 퐸퐺 = √22 − 12 = √3， 9 / 15 故答案为：√3． 17.【答案】 1 【解答】 当푥＝625时，1 5 푥＝125， 当푥＝125时，1 5 푥＝25， 当푥＝25时，1 5 푥＝5， 当푥＝5时，1 5 푥＝1， 当푥＝1时，푥 + 4＝5， 当푥＝5时，1 5 푥＝1， … 依此类推，以5，1循环， (2020 − 2) ÷ 2＝1010， 即输出的结果是1， 18.【答案】 10 【解答】 设每轮传染中平均每人传染了푥人． 依题意，得1 + 푥 + 푥(1 + 푥)＝121， 即(1 + 푥)2＝121， 解方程，得푥1＝10，푥2＝−12（舍去）． 19.【答案】 57 【解答】 第①个图形中一共有3个菱形，即2 + 1 × 1＝3； 第②个图形中一共有7个菱形，即3 + 2 × 2＝7； 第③个图形中一共有13个菱形，即4 + 3 × 3＝13； …， 按此规律排列下去， 所以第⑦个图形中菱形的个数为：8 + 7 × 7＝57． 20.【答案】 휋 4 − 1 2 【解答】 连接퐶퐷，作퐷푀 ⊥ 퐵퐶，퐷푁 ⊥ 퐴퐶． ∵ 퐶퐴＝퐶퐵，∠퐴퐶퐵＝90∘，点퐷为퐴퐵的中点， ∴ 퐷퐶 = 1 2 퐴퐵＝1，四边形퐷푀퐶푁是正方形，퐷푀 = √2 2 ． 则扇形퐹퐷퐸的面积是：90휋×12 360 = 휋 4 ． ∵ 퐶퐴＝퐶퐵，∠퐴퐶퐵＝90∘，点퐷为퐴퐵的中点， ∴ 퐶퐷平分∠퐵퐶퐴， 又∵ 퐷푀 ⊥ 퐵퐶，퐷푁 ⊥ 퐴퐶， ∴ 퐷푀＝퐷푁， ∵ ∠퐺퐷퐻＝∠푀퐷푁＝90∘， ∴ ∠퐺퐷푀＝∠퐻퐷푁， 在△ 퐷푀퐺和△ 퐷푁퐻中， { ∠퐷푀퐺 = ∠퐷푁퐻 ∠퐺퐷푀 = ∠퐻퐷푁 퐷푀 = 퐷푁 ， ∴ △ 퐷푀퐺 ≅△ 퐷푁퐻(퐴퐴푆)， 10 / 15 ∴ 푆四边形퐷퐺퐶퐻＝푆四边形퐷푀퐶푁 = 1 2 ． 则阴影部分的面积是：휋 4 − 1 2 ． 三、解答题（本题 6 小题，共 80 分） 21.【答案】 原式＝4 − √2 − 2 × √2 2 + 1 ＝4 − √2 − √2 + 1 ＝5 − 2√2； 原式＝[ 2(푎−1) (푎−1)(푎+1) + 푎+2 (푎−1)(푎+1)]•푎−1 푎 = 3푎 (푎 − 1)(푎 + 1) ⋅ 푎 − 1 푎 = 3 푎+1 ， 当푎 = √5 − 1时，原式= 3 √5−1+1 = 3√5 5 ． 【解答】 原式＝4 − √2 − 2 × √2 2 + 1 ＝4 − √2 − √2 + 1 ＝5 − 2√2； 原式＝[ 2(푎−1) (푎−1)(푎+1) + 푎+2 (푎−1)(푎+1)]•푎−1 푎 = 3푎 (푎 − 1)(푎 + 1) ⋅ 푎 − 1 푎 = 3 푎+1 ， 当푎 = √5 − 1时，原式= 3 √5−1+1 = 3√5 5 ． 22.【答案】 퐵 （1）（ 3）（ 5） 퐶 【解答】 是旋转图形，不是中心对称图形是正五边形， 故选퐵． 是旋转对称图形，且有一个旋转角是60度的有（1）（ 3）（ 5）． 故答案为（1）（ 3）（ 5）． 命题中①③正确， 故选퐶． 图形如图所示： 23.【答案】 40 54∘ 75人 画树状图得： 11 / 15 ∵ 共有12种等可能的结果，选中小明的有6种情况， ∴ 选中小明的概率为1 2 ． 故答案为：40；54∘；75人． 【解答】 本次抽样测试的学生人数是：12 ÷ 30%＝40（人）； ∵ 퐴级的百分比为： 6 40 × 100%＝15%， ∴ ∠훼＝360∘ × 15%＝54∘； 퐶级人数为：40 − 6 − 12 − 8＝14（人）． 如图所示： 500 × 15%＝75（人）． 故估计优秀的人数为 75人； 画树状图得： ∵ 共有12种等可能的结果，选中小明的有6种情况， ∴ 选中小明的概率为1 2 ． 故答案为：40；54∘；75人． 24.【答案】 解：(1)设去年퐴型车每辆售价푥元， 则今年售价每辆为(푥 − 200)元，由题意得， 80000 푥 = 80000(1−10%) 푥−200 ， 解得：푥 = 2000． 经检验，푥 = 2000是原方程的根． 答：퐴型自行车去年每辆售价为2000元. (2)设今年新进퐴型车푎辆，则퐵型车(60 − 푎)辆，获利푦元，由题意得， 푦 = (1800 − 1500)푎 + (2400 − 1800)(60 − 푎)， 푦 = −300푎 + 36000． ∵ 퐵型车的进货数量不超过퐴型车数量的两倍， ∴ 60 − 푎 ≤ 2푎， 12 / 15 ∴ 푎 ≥ 20． ∵ 푦 = −300푎 + 36000， ∴ 푘 = −300 < 0， ∴ 푦随푎的增大而减小， ∴ 当푎 = 20时，푦有最大值， ∴ 获利最大时퐵型车的数量为：60 − 20 = 40(辆)． ∴ 当新进퐴型车20辆，퐵型车40辆时，这批车获利最大． 【解答】 解：(1)设去年퐴型车每辆售价푥元， 则今年售价每辆为(푥 − 200)元，由题意得， 80000 푥 = 80000(1−10%) 푥−200 ， 解得：푥 = 2000． 经检验，푥 = 2000是原方程的根． 答：퐴型自行车去年每辆售价为2000元. (2)设今年新进퐴型车푎辆，则퐵型车(60 − 푎)辆，获利푦元，由题意得， 푦 = (1800 − 1500)푎 + (2400 − 1800)(60 − 푎)， 푦 = −300푎 + 36000． ∵ 퐵型车的进货数量不超过퐴型车数量的两倍， ∴ 60 − 푎 ≤ 2푎， ∴ 푎 ≥ 20． ∵ 푦 = −300푎 + 36000， ∴ 푘 = −300 < 0， ∴ 푦随푎的增大而减小， ∴ 当푎 = 20时，푦有最大值， ∴ 获利最大时퐵型车的数量为：60 − 20 = 40(辆)． ∴ 当新进퐴型车20辆，퐵型车40辆时，这批车获利最大． 25.【答案】 连接푂퐷、퐷퐵， ∵ 点퐸是线段푂퐵的中点，퐷퐸 ⊥ 퐴퐵交⊙ 푂于点퐷， ∴ 퐷퐸垂直平分푂퐵， ∴ 퐷퐵＝퐷푂． ∵ 在⊙ 푂中，퐷푂＝푂퐵， ∴ 퐷퐵＝퐷푂＝푂퐵， ∴ △ 푂퐷퐵是等边三角形， ∴ ∠퐵퐷푂＝∠퐷퐵푂＝60∘， ∵ 퐵퐶＝푂퐵＝퐵퐷，且∠퐷퐵퐸为△ 퐵퐷퐶的外角， ∴ ∠퐵퐶퐷＝∠퐵퐷퐶 = 1 2 ∠퐷퐵푂． ∵ ∠퐷퐵푂＝60∘， ∴ ∠퐶퐷퐵＝30∘． ∴ ∠푂퐷퐶＝∠퐵퐷푂 + ∠퐵퐷퐶＝60∘ + 30∘＝90∘， ∴ 퐶퐷是⊙ 푂的切线； 答：这个确定的值是1 2 ． 连接푂푃，如图： 13 / 15 由已知可得：푂푃＝푂퐵＝퐵퐶＝2푂퐸． ∴ 푂퐸 푂푃 = 푂푃 푂퐶 = 1 2 ， 又∵ ∠퐶푂푃＝∠푃푂퐸， ∴ △ 푂퐸푃 ∽△ 푂푃퐶， ∴ 푃퐸 푃퐶 = 푂푃 푂퐶 = 1 2 ． 【解答】 连接푂퐷、퐷퐵， ∵ 点퐸是线段푂퐵的中点，퐷퐸 ⊥ 퐴퐵交⊙ 푂于点퐷， ∴ 퐷퐸垂直平分푂퐵， ∴ 퐷퐵＝퐷푂． ∵ 在⊙ 푂中，퐷푂＝푂퐵， ∴ 퐷퐵＝퐷푂＝푂퐵， ∴ △ 푂퐷퐵是等边三角形， ∴ ∠퐵퐷푂＝∠퐷퐵푂＝60∘， ∵ 퐵퐶＝푂퐵＝퐵퐷，且∠퐷퐵퐸为△ 퐵퐷퐶的外角， ∴ ∠퐵퐶퐷＝∠퐵퐷퐶 = 1 2 ∠퐷퐵푂． ∵ ∠퐷퐵푂＝60∘， ∴ ∠퐶퐷퐵＝30∘． ∴ ∠푂퐷퐶＝∠퐵퐷푂 + ∠퐵퐷퐶＝60∘ + 30∘＝90∘， ∴ 퐶퐷是⊙ 푂的切线； 答：这个确定的值是1 2 ． 连接푂푃，如图： 由已知可得：푂푃＝푂퐵＝퐵퐶＝2푂퐸． ∴ 푂퐸 푂푃 = 푂푃 푂퐶 = 1 2 ， 又∵ ∠퐶푂푃＝∠푃푂퐸， ∴ △ 푂퐸푃 ∽△ 푂푃퐶， ∴ 푃퐸 푃퐶 = 푂푃 푂퐶 = 1 2 ． 26.【答案】 ∵ 抛物线푦＝푎푥2 + 푏푥 + 6经过点퐴(6,  0)，퐵(−1,  0)， ∴ { 푎 − 푏 + 6 = 0 36푎 + 6푏 + 6 = 0 ， ∴ {푎 = −1 푏 = 5 ， ∴ 抛物线的解析式为푦＝−푥2 + 5푥 + 6＝−(푥 − 5 2)2 + 49 4 ， ∴ 抛物线的解析式为푦＝−푥2 + 5푥 + 6，顶点坐标为(5 2 , 49 4 )； 由（1）知，抛物线的解析式为푦＝−푥2 + 5푥 + 6， ∴ 퐶(0,  6)， ∴ 푂퐶＝6， ∵ 퐴(6,  0)， ∴ 푂퐴＝6， ∴ 푂퐴＝푂퐶， ∴ ∠푂퐴퐶＝45∘， ∵ 푃퐷平行于푥轴，푃퐸平行于푦轴， 14 / 15 ∴ ∠퐷푃퐸＝90∘，∠푃퐷퐸＝∠퐷퐴푂＝45∘， ∴ ∠푃퐸퐷＝45∘， ∴ ∠푃퐷퐸＝∠푃퐸퐷， ∴ 푃퐷＝푃퐸， ∴ 푃퐷 + 푃퐸＝2푃퐸， ∴ 当푃퐸的长度最大时，푃퐸 + 푃퐷取最大值， ∵ 퐴(6,  0)，퐶(0,  6)， ∴ 直线퐴퐶的解析式为푦＝−푥 + 6， 设퐸(푡, −푡 + 6)(0 < 푡 < 6)，则푃(푡, −푡2 + 5푡 + 6)， ∴ 푃퐸＝−푡2 + 5푡 + 6 − (−푡 + 6)＝−푡2 + 6푡＝−(푡 − 3)2 + 9， 当푡＝3时，푃퐸最大，此时，−푡2 + 5푡 + 6＝12， ∴ 푃(3,  12)； 如图(2)，设直线퐴퐶与抛物线的对称轴푙的交点为퐹，连接푁퐹， ∵ 点퐹在线段푀푁的垂直平分线퐴퐶上， ∴ 퐹푀＝퐹푁，∠푁퐹퐶＝∠푀퐹퐶， ∵ 푙 // 푦轴， ∴ ∠푀퐹퐶＝∠푂퐶퐴＝45∘， ∴ ∠푀퐹푁＝∠푁퐹퐶 + ∠푀퐹퐶＝90∘， ∴ 푁퐹 // 푥轴， 由（2）知，直线퐴퐶的解析式为푦＝−푥 + 6， 当푥 = 5 2 时，푦 = 7 2 ， ∴ 퐹(5 2 , 7 2)， ∴ 点푁的纵坐标为7 2 ， 设푁的坐标为(푚, −푚2 + 5푚 + 6)， ∴ −푚2 + 5푚 + 6 = 7 2 ，解得，푚 = 5+√35 2 或푚 = 5−√35 2 ， ∴ 点푁的坐标为(5+√35 2 , 7 2)或(5−√35 2 , 7 2)． 【解答】 ∵ 抛物线푦＝푎푥2 + 푏푥 + 6经过点퐴(6,  0)，퐵(−1,  0)， ∴ { 푎 − 푏 + 6 = 0 36푎 + 6푏 + 6 = 0 ， ∴ {푎 = −1 푏 = 5 ， ∴ 抛物线的解析式为푦＝−푥2 + 5푥 + 6＝−(푥 − 5 2)2 + 49 4 ， ∴ 抛物线的解析式为푦＝−푥2 + 5푥 + 6，顶点坐标为(5 2 , 49 4 )； 由（1）知，抛物线的解析式为푦＝−푥2 + 5푥 + 6， ∴ 퐶(0,  6)， ∴ 푂퐶＝6， ∵ 퐴(6,  0)， ∴ 푂퐴＝6， 15 / 15 ∴ 푂퐴＝푂퐶， ∴ ∠푂퐴퐶＝45∘， ∵ 푃퐷平行于푥轴，푃퐸平行于푦轴， ∴ ∠퐷푃퐸＝90∘，∠푃퐷퐸＝∠퐷퐴푂＝45∘， ∴ ∠푃퐸퐷＝45∘， ∴ ∠푃퐷퐸＝∠푃퐸퐷， ∴ 푃퐷＝푃퐸， ∴ 푃퐷 + 푃퐸＝2푃퐸， ∴ 当푃퐸的长度最大时，푃퐸 + 푃퐷取最大值， ∵ 퐴(6,  0)，퐶(0,  6)， ∴ 直线퐴퐶的解析式为푦＝−푥 + 6， 设퐸(푡, −푡 + 6)(0 < 푡 < 6)，则푃(푡, −푡2 + 5푡 + 6)， ∴ 푃퐸＝−푡2 + 5푡 + 6 − (−푡 + 6)＝−푡2 + 6푡＝−(푡 − 3)2 + 9， 当푡＝3时，푃퐸最大，此时，−푡2 + 5푡 + 6＝12， ∴ 푃(3,  12)； 如图(2)，设直线퐴퐶与抛物线的对称轴푙的交点为퐹，连接푁퐹， ∵ 点퐹在线段푀푁的垂直平分线퐴퐶上， ∴ 퐹푀＝퐹푁，∠푁퐹퐶＝∠푀퐹퐶， ∵ 푙 // 푦轴， ∴ ∠푀퐹퐶＝∠푂퐶퐴＝45∘， ∴ ∠푀퐹푁＝∠푁퐹퐶 + ∠푀퐹퐶＝90∘， ∴ 푁퐹 // 푥轴， 由（2）知，直线퐴퐶的解析式为푦＝−푥 + 6， 当푥 = 5 2 时，푦 = 7 2 ， ∴ 퐹(5 2 , 7 2)， ∴ 点푁的纵坐标为7 2 ， 设푁的坐标为(푚, −푚2 + 5푚 + 6)， ∴ −푚2 + 5푚 + 6 = 7 2 ，解得，푚 = 5+√35 2 或푚 = 5−√35 2 ， ∴ 点푁的坐标为(5+√35 2 , 7 2)或(5−√35 2 , 7 2)．