2020-2021学年人教版九年级期末数学模拟试卷 7页

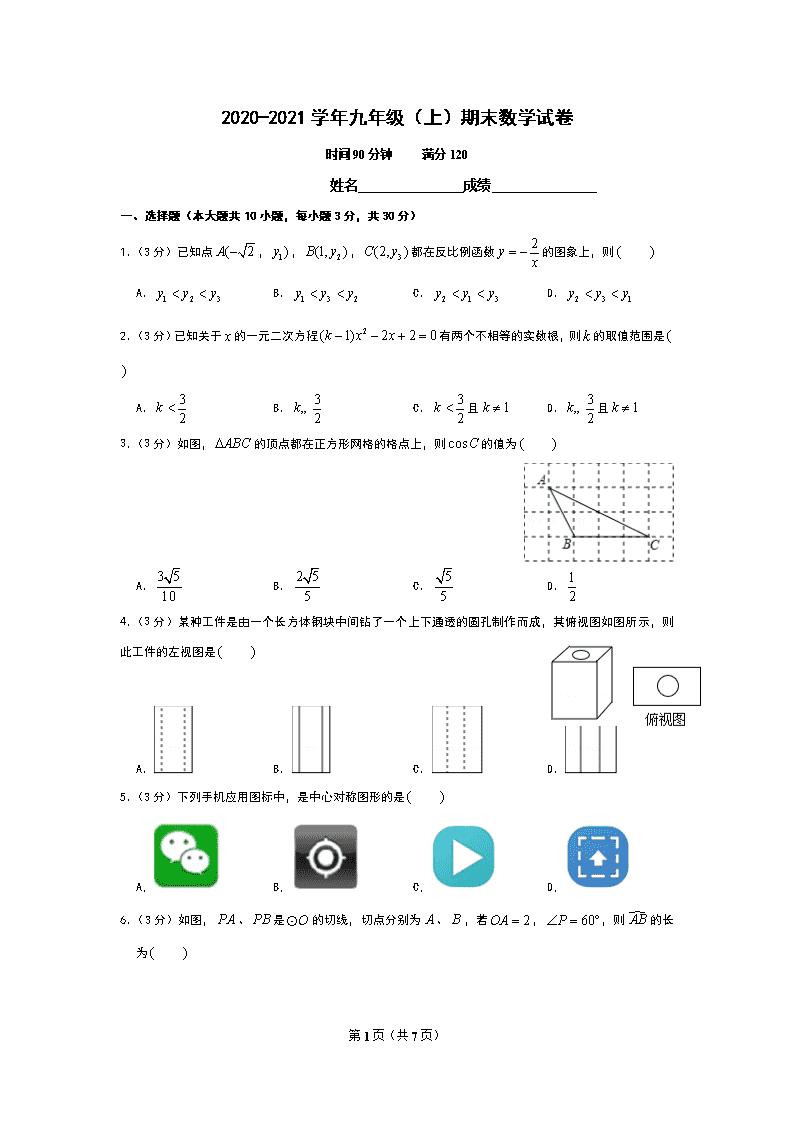
第 1页（共 7页） 2020-2021 学年九年级（上）期末数学试卷 时间 90 分钟 满分 120 姓名 成绩 一、选择题（本大题共 10 小题，每小题 3 分，共 30 分） 1．（3 分）已知点 ( 2A  ， 1)y ， 2(1, )B y ， 3(2, )C y 都在反比例函数 2y x   的图象上，则 ( ) A． 1 2 3y y y  B． 1 3 2y y y  C． 2 1 3y y y  D． 2 3 1y y y  2．（3 分）已知关于 x 的一元二次方程 2( 1) 2 2 0k x x    有两个不相等的实数根，则 k 的取值范围是 ( ) A． 3 2k  B． 3 2k„ C． 3 2k  且 1k  D． 3 2k„ 且 1k  3．（3 分）如图， ABC 的顶点都在正方形网格的格点上，则 cosC 的值为 ( ) A． 3 5 10 B． 2 5 5 C． 5 5 D． 1 2 4．（3 分）某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成，其俯视图如图所示，则 此工件的左视图是 ( ) A． B． C． D． 5．（3 分）下列手机应用图标中，是中心对称图形的是 ( ) A． B． C． D． 6．（3 分）如图， PA 、 PB 是 O 的切线，切点分别为 A 、 B ，若 2OA  ， 60P   ，则 AB 的长 为 ( ) 第 2页（共 7页） A． 2 3  B． C． 4 3  D． 5 3  7．（3 分）如图显示了用计算机模拟随机投掷一枚图钉的实验结果．随着试验次数的增加，“钉尖向上”的 频率总在某个数字附近，显示出一定的稳定性，可以估计“钉尖向上”的概率是 ( ) A．0.620 B．0.618 C．0.610 D．1000 8．（3 分）若将抛物线 25y x 先向右平移 2 个单位，再向上平移 1 个单位，得到的新抛物线的表达式为 ( ) A． 25( 2) 1y x   B． 25( 2) 1y x   C． 25( 2) 1y x   D． 25( 2) 1y x   9．（3 分）如图，抛物线 2y ax bx c   的对称轴为 1x   ，且过点 1( ,0)2 ，有下列结论：其中正确的 结论是 ( ) ① 0abc  ；② 2 4 0a b c   ；③ 2 0a b  ；④ 3 2 0b c  ． A．①③ B．①④ C．①② D．②④ 10．（3 分）如图，在矩形 ABCD 中， 4AB  ， 6BC  ， E 是矩形内部的一个动点，且 AE BE ，则线 段 CE 的最小值为 ( ) A． 3 2 B． 2 10 2 C． 2 13 2 D．4 二、填空题（共 4 小题，共 12 分） 11．（4 分）设 m 、 n 分别为方程 2 2 2021 0x x   的两个实数根，则 2 3m m n   ． 12．（4 分）如图，在 ABC 中， 4AB  ， 3AC  ， 30BAC   ，将 ABC 绕点 A 逆时针旋转 60 得到△ 1 1AB C ，连接 1BC ，则 1BC 的长为 ． 第 3页（共 7页） 13．（4 分）如图，在 O 中，半径 OC 与弦 AB 垂直于点 D ，且 8AB  ， 5OC  ，则 CD 的长是 ． 14．（4 分）某一型号飞机着陆后滑行的距离 y （单位： )m 与滑行时间 x （单位： )s 之间的函数关系式是 240 2y x x  ，该型号飞机着陆后需滑行 m 才能停下来． 15．（4 分）在一个口袋中有 4 个完全相同的小球，把它们分别标号为 1，2，3，4，随机地摸出一个小球不 放回，再随机地摸出一个小球，则两次摸出的小球的标号的和为奇数的概率是 ． 16. （4 分）方程 2 2020x x 的解是 ． 17．（4 分）如图，在正方形 ABCD 中， BPC 是等边三角形， BP 、 CP 的延长线分别交 AD 于点 E 、 F ，连结 BD 、 DP ， BD 与 CF 相交于点 H ．给出下列结论，其中正确结论的个数有 （请填序号）① BDE DPE ∽ ；② 2 3 3 FP FH  ；③ 2DP PH PB  ；④ tan 2 3DBE   ． 三、解答题（本大题共 3 小题，每题 6 分，共 18 分） 18．（6 分）当 12 1x   ，求 2 1( ) (1 )1 1 xx x x     的值． 第 4页（共 7页） 19．（6 分） ABC 在平面直角坐标系 xOy 中的位置如图所示． （1）作 ABC 关于点 C 成中心对称的△ 1 1A B C ． （2）作△ 1 1A B C 绕点 O 顺时针旋转 90 后的△ 2 2 2A B C ． 20．（6 分）为了了解学生毕业后就读普通高中或就读中等职业技术学校的意向，某校对八、九年级部分学 生进行了一次调查，调查结果有三种情况： A ．只愿意就读普通高中； B ．只愿意就读中等职业技术学校； C ．就读普通高中或中等职业技术学校都愿意． 学校教务处将调查数据进行了整理，并绘制了尚不完整的统计图，如图，请根据相关信息，解答下列问题： （1）本次活动共调查了 名学生． （2）补全图 1，并求出图 2 中 B 区域的圆心角的度数； （3）若该校八、九年级学生共有 2800 名，请估计该校学生只愿意就读普通高中的概率． 第 5页（共 7页） 四、解答题（本大题共 3 小题，每题 8 分，共 24 分） 21．（6 分）如图，线段 AB 、 CD 分别表示甲、乙两建筑物的高， BA AD ， CD DA ，垂足分 别为 A 、D ．从 D 点测到 B 点的仰角 为 60 ，从 C 点测得 B 点的仰角  为 30 ，甲建筑物的高 30AB  米． （1）求甲、乙两建筑物之间的距离 AD ． （2）求乙建筑物的高 CD ． 22．俄罗斯世界杯足球赛期间，某商店销售一批足球纪念册，每本进价 40 元，规定销售单价不低于 44 元， 且获利不高于 30% ．试销售期间发现，当销售单价定为 44 元时，每天可售出 300 本，销售单价每上涨 1 元，每天销售量减少 10 本，现商店决定提价销售．设每天销售量为 y 本，销售单价为 x 元． （1）请直接写出 y 与 x 之间的函数关系式和自变量 x 的取值范围； （2）将足球纪念册销售单价定为多少元时，商店每天销售纪念册获得的利润 w 元最大？最大利润是多少 元？ 第 6页（共 7页） 23．如图，在平行四边形 ABCD 中，过点 A 作 AE DC ，垂足为 E ，连接 BE ， F 为 BE 上一点，且 AFE D   ． （1）求证： ABF BEC ∽ ； （2）若 5AD  ， 8AB  ， 4sin 5D  ，求 AF 的长． 四、解答题（本大题共 2 小题，每题 10 分，共 20 分） 24．（10 分）如图，已知 AB 是 O 的直径，点 C 在 O 上，过点 C 的直线与 AB 的延长线交于点 P ， AC PC ， 2COB PCB   ． （1）求证： PC 是 O 的切线； （2）求证： 1 2BC AB ； （3）点 M 是弧 AB 的中点， CM 交 AB 于点 N ，若 8AB  ，求 MN MC 的值． 第 7页（共 7页） 25．（10 分）在平面直角坐标系中，我们定义直线 y ax a  为抛物线 2 (y ax bx c a   、b 、c 为常数， 0)a  的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在 y 轴上的三角形为其“梦想三角形”． 已知抛物线 22 3 4 3 2 33 3y x x    与其“梦想直线”交于 A 、B 两点（点 A 在点 B 的左侧），与 x 轴负半轴交于点 C ． （1）填空：该抛物线的“梦想直线”的解析式为 ，点 A 的坐标为 ，点 B 的坐标为 ； （2）如图，点 M 为线段 CB 上一动点，将 ACM 以 AM 所在直线为对称轴翻折，点 C 的对称点为 N ， 若 AMN 为该抛物线的“梦想三角形”，求点 N 的坐标； （3）当点 E 在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点 F ，使得以点 A 、 C 、 E 、 F 为顶点的四边形为平行四边形？若存在，请直接写出点 E 、 F 的坐标；若不存在，请说明理 由．