2019九年级数学上册 专题突破讲练 认识圆的轴对称性试题 （新版）青岛版 8页

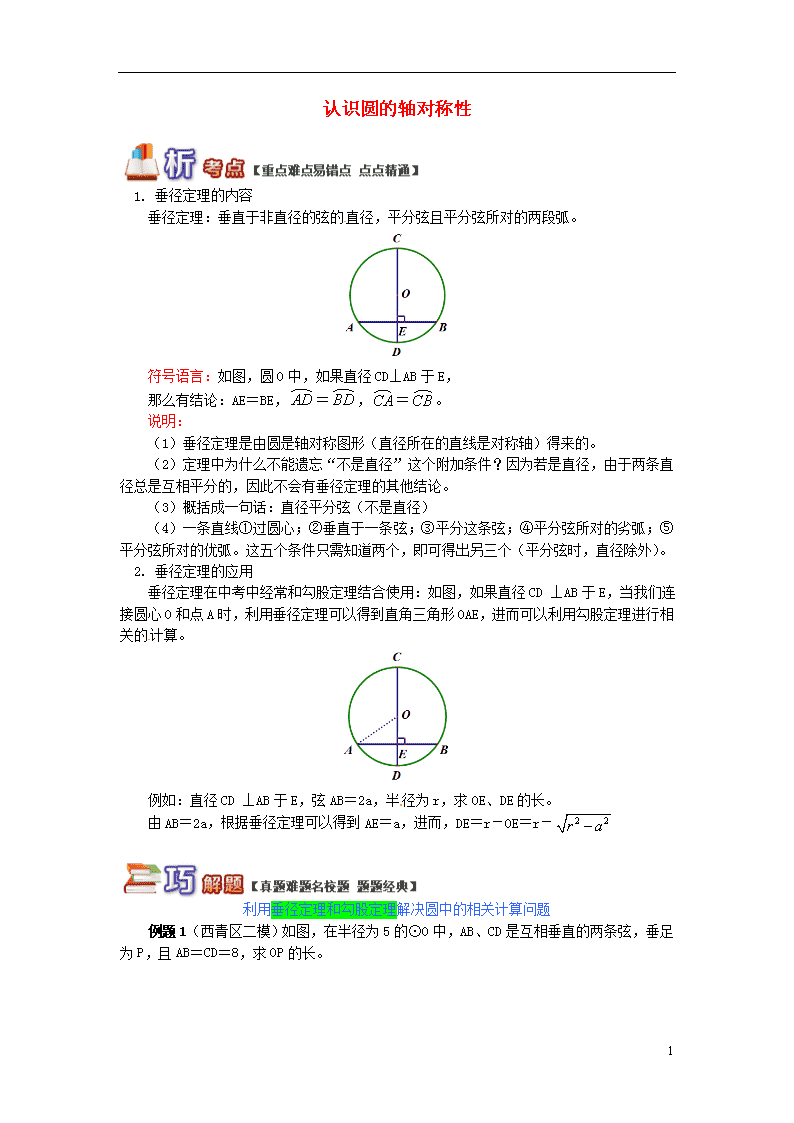
认识圆的轴对称性 ‎1. 垂径定理的内容 垂径定理：垂直于非直径的弦的直径，平分弦且平分弦所对的两段弧。‎ 符号语言：如图，圆O中，如果直径CD⊥AB于E，‎ 那么有结论：AE＝BE，＝，＝。‎ 说明：‎ ‎（1）垂径定理是由圆是轴对称图形（直径所在的直线是对称轴）得来的。‎ ‎（2）定理中为什么不能遗忘“不是直径”这个附加条件？因为若是直径，由于两条直径总是互相平分的，因此不会有垂径定理的其他结论。‎ ‎（3）概括成一句话：直径平分弦（不是直径）‎ ‎（4）一条直线①过圆心；②垂直于一条弦；③平分这条弦；④平分弦所对的劣弧；⑤平分弦所对的优弧。这五个条件只需知道两个，即可得出另三个（平分弦时，直径除外）。‎ ‎2. 垂径定理的应用 垂径定理在中考中经常和勾股定理结合使用：如图，如果直径CD ⊥AB于E，当我们连接圆心O和点A时，利用垂径定理可以得到直角三角形OAE，进而可以利用勾股定理进行相关的计算。‎ 例如：直径CD ⊥AB于E，弦AB＝‎2a，半径为r，求OE、DE的长。‎ 由AB＝‎2a，根据垂径定理可以得到AE＝a，进而，DE＝r－OE＝r－‎ 利用垂径定理和勾股定理解决圆中的相关计算问题 例题1 （西青区二模）如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB＝CD＝8，求OP的长。 ‎ 8‎ ‎ ‎ 解析：作OM⊥AB于M，ON⊥CD于N，连接OP，OB，OD，首先利用勾股定理求得OM的长，然后判定四边形OMPN是正方形，求得正方形的对角线的长即可求得OM的长。‎ 解：作OM⊥AB于M，ON⊥CD于N，连接OP，OB，OD，‎ ‎∵AB＝CD＝8，‎ ‎∴BM＝DN＝4，‎ ‎∴OM＝ON＝‎ ‎∵AB⊥CD，‎ ‎∴∠DPB＝90°，‎ ‎∵OM⊥AB于M，ON⊥CD于N，‎ ‎∴∠OMP＝∠ONP＝90°‎ ‎∴四边形MONP是矩形，‎ ‎∵OM＝ON，‎ ‎∴四边形MONP是正方形，‎ ‎∴OP＝‎ 点拨：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键。‎ 例题2 （长春）如图，将一个两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D、E，量出半径OC＝‎5cm，弦DE＝‎8cm，求直尺的宽。‎ 解析：这是一个关系到弦长和半径的问题，因此我们考虑运用垂径定理来解决。‎ 解：过点O作OM⊥DE于点M，连接OD。‎ ‎∴DM＝DE。‎ ‎∵DE＝8，‎ ‎∴DM＝4。‎ 在Rt△ODM中，∵OD＝OC＝5，‎ ‎∴OM＝＝‎ ‎∴直尺的宽度为‎3cm。‎ 点拨：这是一个非常贴近学生生活的实际问题，由问题背景我们可以发现，利用垂径定理构造出合适的直角三角形来解决此类问题。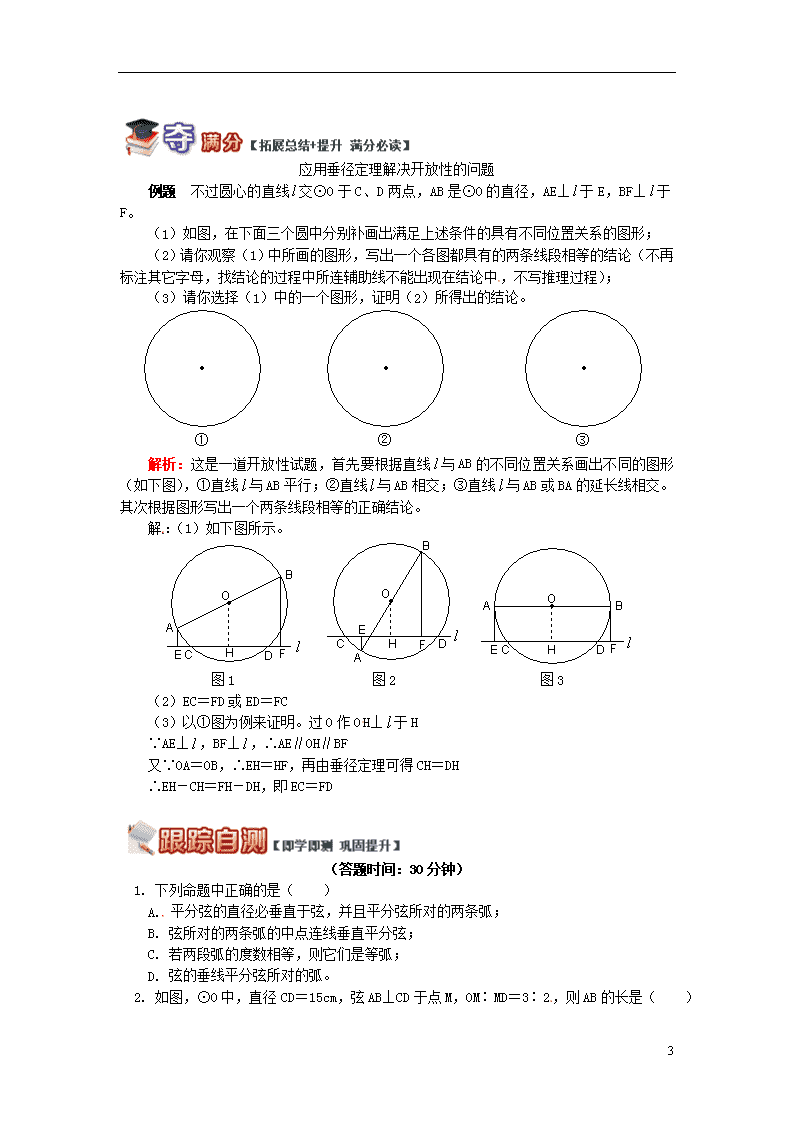‎ 8‎ 应用垂径定理解决开放性的问题 例题 不过圆心的直线交⊙O于C、D两点，AB是⊙O的直径，AE⊥于E，BF⊥于F。‎ ‎（1）如图，在下面三个圆中分别补画出满足上述条件的具有不同位置关系的图形；‎ ‎（2）请你观察（1）中所画的图形，写出一个各图都具有的两条线段相等的结论（不再标注其它字母，找结论的过程中所连辅助线不能出现在结论中，不写推理过程）；‎ ‎（3）请你选择（1）中的一个图形，证明（2）所得出的结论。‎ ‎ ‎ 解析：这是一道开放性试题，首先要根据直线与AB的不同位置关系画出不同的图形（如下图），①直线与AB平行；②直线与AB相交；③直线与AB或BA的延长线相交。其次根据图形写出一个两条线段相等的正确结论。‎ 解：（1）如下图所示。‎ ‎ ‎ ‎ 图1 图2 图3‎ ‎（2）EC＝FD或ED＝FC ‎（3）以①图为例来证明。过O作OH⊥于H ‎∵AE⊥，BF⊥，∴AE∥OH∥BF 又∵OA＝OB，∴EH＝HF，再由垂径定理可得CH＝DH ‎ ‎∴EH－CH＝FH－DH，即EC＝FD ‎（答题时间：30分钟）‎ ‎1. 下列命题中正确的是（ ）‎ A. 平分弦的直径必垂直于弦，并且平分弦所对的两条弧；‎ B. 弦所对的两条弧的中点连线垂直平分弦；‎ C. 若两段弧的度数相等，则它们是等弧；‎ D. 弦的垂线平分弦所对的弧。‎ ‎2. 如图，⊙O中，直径CD＝‎15cm，弦AB⊥CD于点M，OM∶MD＝3∶2，则AB的长是（ ）‎ 8‎ A. ‎7.5‎cm‎ B. ‎15cm C. ‎12cm D. ‎‎12.5cm ‎3. 已知⊙O的半径为‎10cm，弦AB∥CD，AB＝‎12cm，CD＝‎16cm，则AB和CD的距离是（ ）‎ A. ‎2cm B. ‎14cm C. ‎2cm或‎14cm D. ‎2cm或‎12cm ‎4. 若圆中一弦与弦高之和等于直径，弦高为1，则圆的半径为（ ）‎ A. 1 B. C. 2 D. ‎ ‎5. 在半径为‎5cm的⊙O中，有一点P满足OP＝‎3 cm，则过P的整数弦有___________条。‎ ‎6. 等腰△ABC中，AB＝AC，∠A＝120°，BC＝‎10 cm，则△ABC的外接圆半径为________。‎ ‎7. 圆内一弦与直径相交成30°的角，且分直径为‎1 cm和‎5 cm两段，则此弦长为_________。‎ ‎8. 如图，AB为⊙O的直径，AC为弦，OD⊥AC于D，BD交OC于E，若AC＝4，AB＝5，则BE＝_________。‎ ‎9. 如图，已知⊙O1与⊙O2相交于A、B两点，C、A、D三点在一条直线上，CD的延长线交O1 O2的延长线于P，∠P＝30°，，则CD＝________。‎ ‎10. 如图，是一块残破的圆轮片，A、B、C是圆弧上的三点。‎ ‎（1）作出弧ACB所在的⊙O（不写作法，保留作图痕迹）；‎ ‎（2）如果AC＝BC＝‎60cm，∠ACB＝120°，求该残破圆轮片的半径。‎ ‎11. 如图，Rt△ABC中，∠C＝90°，AC＝3，BC＝4，以点C为圆心，CA为半径的圆与AB、BC分别交于点D、E，求AB、AD的长。‎ 8‎ ‎12. 如图，⊙O的半径为‎10cm，G是直径AB上一点，弦CD经过点G，CD＝‎16cm，AE⊥CD于E，BF⊥CD于F，求AE－BF的值。‎ 8‎ ‎ ‎ ‎1. B 解析：平分弦（非直径）的直径垂直于弦，并且平分弦所对的两条弧，故A错误；能重合的弧才是等弧，必须是弧所对的圆心角和所在圆的半径都相等的弧才能叫做等弧，故C错误；只有弦的垂直平分线才能够平分弧，故D错误。 ‎ ‎2. C 解析：连接AO，∵OM∶MD＝3∶2且直径CD＝‎15cm，∴易求得，，根据已知条件易证△AMO为Rt△，‎ ‎∴cm，根据垂径定理可知，∴AB长为‎12cm。所以C选项正确。‎ ‎3. C 解析：本题在解题过程中一定要注意分类讨论的思想，通过分析题意，本题有两种可能性，AB、CD可能在圆心的同侧也可能在异侧，当AB、CD在同侧时，如图1所示，根据条件易求得，，；当AB、CD在圆心的异侧时，，，。所以C选项正确。‎ ‎ ‎ ‎4. D 解析：本题涉及一个概念——弦高，所谓弦高是指弦的垂直平分线与劣弧的交点与垂足之间的线段长。∴根据题意易知，如图所示，设半径为r，∴，，，再由勾股定理，就可求得或（舍），∴。所以D选项正确。‎ ‎5. 4 解析：由题意分析可知过点P的弦最短为8，即过点P恰好与OP垂直的弦，最长为10，即与OP重合的直径，8与10中间还有一个整数9，再据圆的轴对称性可知长度为9的有两条，∴过点P的整数弦有4条。‎ ‎6. cm 解析：如图所示，依据垂径定理以及勾股定理可求得，外接圆的半径为cm。‎ 8‎ ‎7. cm 解析：根据题意易求得，又∵，∴，再在Rt△DOH中，据勾股定理可求得，∴。所以此弦长为。‎ ‎8. 解析：本题考查的知识点较多，包括垂径定理，相似，勾股定理等，连接BC，AB为⊙O的直径，AC为弦，OD⊥AC于D，AC＝4，AB＝5，∴BC＝3，易证，又∵O是圆心，∴，∴，在Rt△BCD中，据勾股定理，易求得，∴。‎ ‎9. 6 解析：如图所示，分别过两个圆心作CP的垂线，∴，所以要想求出CD的长度，只需要求出MH即可知道CD的长。又过作于点I，在Rt△中根据勾股定理可求得，∴CD＝6。‎ ‎10. 解析：①利用垂径定理得出AC，BC的垂直平分线，交点即是圆心，到任意一点的距离即是半径；②利用垂径定理以及等边三角形的判定得出△OBC是等边三角形，即可得出答案。‎ 解：（1）如图1所示：‎ ‎（2）如图2，∵AC＝BC＝‎60cm，∠ACB＝120°‎ 8‎ ‎∴∠AOC＝∠BOC，‎ 又∵AO＝CO，CO＝BO，‎ ‎∴△AOC≌△COB，‎ ‎∴∠CBO＝∠ACO＝60°，‎ ‎∵BO＝CO，‎ ‎∴∠OBC＝∠BCO＝60°，‎ ‎∴△OBC是等边三角形，‎ ‎∴半径为‎60cm。‎ ‎11. 解析：∵∠C＝90°，AC＝3，BC＝4，∴AB＝5，过点C作CH⊥AB于点H，利用面积相等建立等式，∴，在Rt△ACH中，可求得，‎ ‎∴据垂径定理可得：。‎ ‎12. 解：连结OC，过点O作OM⊥CD于M，则CM＝MD ‎ ‎∵CD＝‎16cm，AB＝‎8 cm，在Rt△OMC中，因OC＝‎‎10 cm ‎∴OM＝cm ‎∵AE⊥CD，BF⊥CD，OM⊥CD，∴AE∥OM∥BF ‎∴，‎ ‎∴cm ‎∴AE－BF＝2OM＝‎‎12 cm 8‎