华师版数学九年级下册课件-第26章 二次函数-26 实践与探索 23页

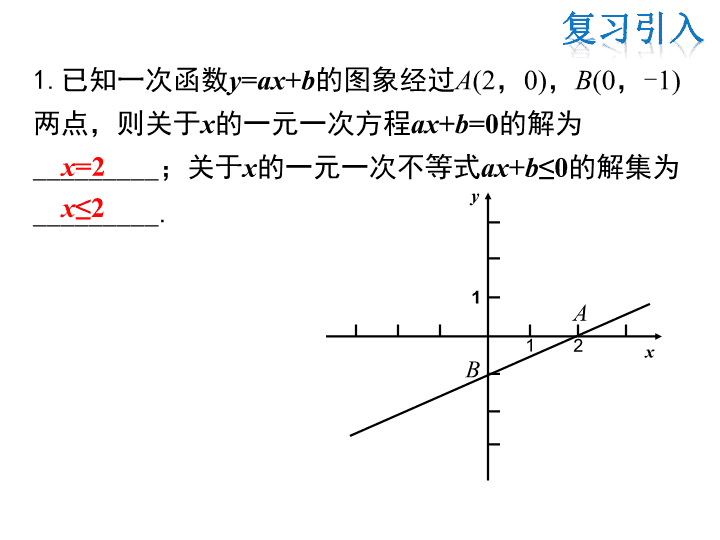
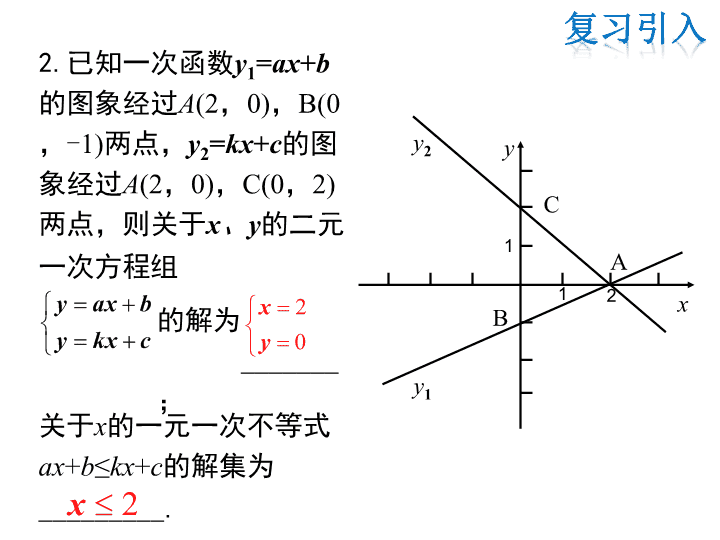
HS九(下) 教学课件 26.3 实践与探索 第26章 二次函数 第3课时 利用两个函数的图象求方程(组) 和不等式的解集 1.已知一次函数y=ax+b的图象经过A(2，0)，B(0，-1) 两点，则关于x的一元一次方程ax+b=0的解为 _________；关于x的一元一次不等式ax+b≤0的解集为 _________. x=2 x≤2 1 1 2 x y A B 1 1 2 y2 y1 x y A B C 2.已知一次函数y1=ax+b 的图象经过A(2，0)，B(0， -1)两点，y2=kx+c的图象 经过A(2，0)，C(0，2)两 点，则关于x、y的二元一 次方程组 关于x的一元一次不等式 ax+b≤kx+c的解集为 _________.      y ax b y kx c 的解为 _______； 2 0    x y 2x 3.已知二次函数 ，该函数图象与y轴的 交点坐标为_______,与x轴的交点坐标为 _________________;画出该函数草图，根据图象可 知当______________时，y＞0. 2 5 6  y x x x-6 1 y (0，-6) (-6，0)，(1，0) x<-6或x>1 4.已知二次函数 的图象如图所示，则 一元二次方程 的解为___________;当 ____________时y＜0;当__________时y随x的增大而 减小. 2  y ax bx c 2 0  =ax bx c -4 2 x y x1=-4，x2=2 x<-4或x>2 -1 x>-1 x y k 2 k 1 2y ax bx c   已知二次函数 的图象如图所示：2  y ax bx c 通过观察以下图象，一元二次方程 的 解是_______________. 2 0ax bx c   x1=k1，x2=k2 二次函数的图 象与x轴的交点. y=0 利用两个函数图象求方程或方程组的解1 (x2, h) 2 2 2 2( , )x ax bx c x y k2k1 2  y ax bx c 2 0  ax bx c 问题1 二次函数 的图象与x轴（直线y=0） 的交点的横坐标是一元二次方程 的根， 那么，二次函数 与直线y=h的交点的横坐 标是否也是某一个一元二次方程的根呢？ 2  y ax bx c y h 这个点的坐标有 几种表示方式？ 方程 的实数根. 2   ax bx c h 2  y ax bx c 2y ax x y x1 x2 2y ax  y bx c 问题2 如图，二次函数 的图象与一次函数 的图象交于两点，观察以下图象，你能得到哪些信息？  y bx c x1 , x2 可以看做是方程 的解.2  ax bx c (x1，y1 ), (x2，y2 ) 也可以看做 是方 程组 的解. 2     y ax y bx c 2 x y -2 0 4-2-4 -4 -6 -8 利用二次函数的图象求一元二次方程x2+2x-1=3 的近似根. 解：(1)原方程可变形为 x2+2x-4=0； (3)观察估计抛物线 y=x2+2x-4和x轴的交 点的横坐标； (2)用描点法作二次 函数y=x2+2x-4的图象； 例1 由图象可知,它们有两个交点,其横坐标一个在-4与 -3之间,另一个在1与2之间,分别约为-3.2和1.2. （4）由此可知,一元二次方程x2+2x-1=3的近 似根为：x1≈3.2,x2≈1.2. 想一想：还有没有别的办法求这个方程的近似根？ (1)用描点法作二次函数y=x2+2x-1的图象； (3)观察估计抛物线y=x2+2x-1和 直线y=3的交点的横坐标； (2)作直线y=3； 方法二： 2 x y 2 4 4-2-4 0 -2 -4 由图象可知,它们有两个交点,其 横坐标一个在-4与-3之间,另一个 在1与2之间,分别约为-3.2和1.2. （4）由此可知,一元二次方程 x2+2x-1=3的近似根为x1≈3.2,x2≈1.2. 方法三： (1)作二次函数y=x2的图象； (2)作一次函数y=-2x+4的图象； (3)观察估计抛物线y=x2+2x-1和 直线y=3的交点的横坐标； 由图象可知,它们有两个交点,其 横坐标一个在-4与-3之间,另一个 在1与2之间,分别约为-3.2和1.2. （4）由此可知,一元二次方程 x2+2x-1=3的近似根为x1≈3.2,x2≈1.2. 2 x y 2 4 4-2-4 o -2 两个函数图象的交点坐标就是对应函数解 析式所组成的方程组的解. 函数解析式对应方程的根，就是该函数图 象与x轴交点的横坐标； 归纳总结 利用两个函数图象求不等式的解集 已知抛物线 (a＞0）与直线 相交于点O（0,0）和点A（3,2），求不等式 的解集. 2 y ax bx y kx 2  ＞ax bx kx 分析：根据题目提供的条件，无法求出抛物线的解 析式.因此，我们可以换一个思路，利用函数的图象 来判求不等式的解集. 2 例2 解：根据题目提供的条件，画出草图： x y O 3 2 2  ＞ax bx kx 2  ＞ax bx kx 2  ＜ax bx kx 3＞x 0 3＜ ＜x 0＜x 由图可知，不等式 的解集为 或 . 2  ＞ax bx kx 0＜x 3＞x 不等式 的解集是二次函数 的图象在直线 上方 的点的横坐标所组成的范围. 2   ＞ax bx c mx n 2  y ax bx c  y mx n 不等式 的解集是二次函数 的图象在直线 下方的 点的横坐标所组成的范围. 2   ＜ax bx c mx n 2  y ax bx c  y mx n 方法总结 已知函数y1＝x2与函数 的图象大致如 图，若y1＜y2，则自变量x的取值范围是( ) 2 1 32  y x A. 3 22 x ＜ ＜ C. 32 2x ＜ ＜ B. 或2x＜- 3 2x＞ D. 或3 2x＜- 2x＞ C 解析：先根据方程 算出图象交点的 横坐标，然后再结合图象，得出答案. 2 1 32  x x 3 22 1.若二次函数y=x2+bx的图象的对称轴是经过点（2,0） 且平行于y轴的直线，则关于x的方程x2+bx=5的解为 （ ） A. x1=0, x2=4 B. x1=1, x2=5 C. x1=1, x2= -5 D. x1= -1, x2=5 2.若二次函数y=ax2+bx+c(a＜0）的图象经过（2,0）， 且其对称轴为x=-1，则使函数值y＞0成立的x的取值范 围是 （ ） A. x＜-4或 x＞2 B. -4≤x≤2 C. x≤-4或 x≥2 D. -4＜x＜2 D D 3.二次函数y=ax2+bx+c(a≠0，a,b,c为常数）的图象如 图所示，则方程ax2+bx+c=m有实数根的条件是 （ ） A.m≥-2 B.m≥5 C.m≥0 D.m≥4 解析：方程ax2+bx+c=m 有实数根，即表示二次函 数y=ax2+bx+c的图象与直 线y=m有交点. A 4.如图，一次函数y1=kx+1与二次函数y2=ax2+bx-2交 于A、B两点，且A（1,0），抛物线的对称轴是 . （1） 求k和a、b的值； （2）求不等式 kx+1＞ax2+bx-2的解集. 3 2x   x y AO B 2y 1y 解：（1）y1=kx+1经过点A（1,0）， 则0=k+1，得k=-1. y=ax2+bx-2经过点A（1,0）， 则0=a+b-2 ①， 抛物线的对称轴是 ， 故 ② ，联立① ②， 解得 3 2x   3 2 2 b a    1 3, .2 2a b  （2）根据对称性，可知y2与x轴的另一个交点为 （-4,0），根据图象可以看出，kx+1＞ax2+bx-2的 解集为-4＜x＜1. x y AO B 2y 1y 2ax bx c h   变 形 函数图象交点 的横坐标 2y ax y bx c       2y ax bx x y h       2 0ax bx c   变 形 函数图象交点 的横坐标 2ax bx c mx n  ＞ 2ax bx c mx n  ＜ 变 形 变 形 2y ax bx x y mx n        解集是抛物线图象在 直线下方的点的横坐 标所组成的取值范围 解集是抛物线图象在 直线上方的点的横坐 标所组成的取值范围