华东师大版数学中考专题复习与训练课件-第1篇 第4章 4 一般三角形与多边形 65页

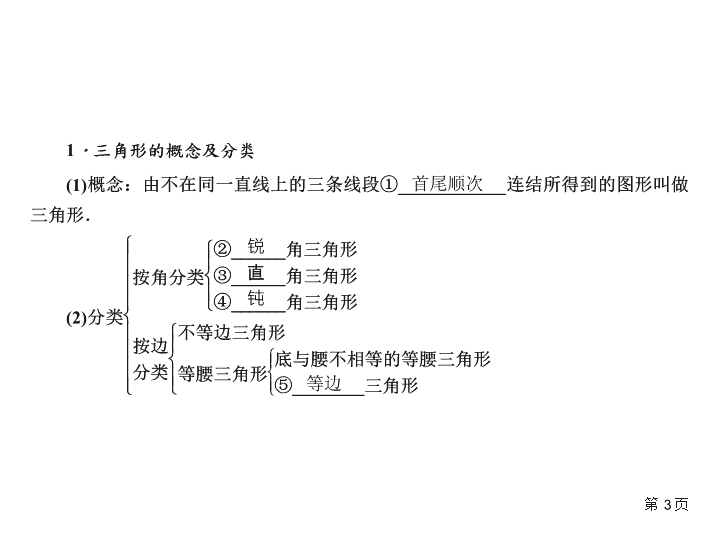
第一篇 过教材·考点透析 第四章　三角形 4.2　一般三角形与多边形 第 2 页 第 3 页 首尾顺次　 锐　 直　 钝　 等边　 § 方法点拨：(1)组成三角形的三条线段要“不在同一直线上”，如 果在同一直线上，三角形就不存在；(2)三条线段“首尾顺次连 结”，是指三条线段两两之间有一个公共端点，这个公共端点就 是三角形的顶点． 第 4 页 第 5 页 角平分线　 相等　 内部　 内心　 § 方法点拨：一般利用角平分线上的点到角两 边的距离相等这一性质证线段相等或构造全 等三角形等． 第 6 页 第 7 页 中线　 内部　 重心　 相等　 § 方法点拨：(1)如图，若AD为△ABC的BC边 上的中线，则△BAD与△CAD的周长之差为 AB－AC． § (2)重心到三角形顶点的距离等于它到对边中 点距离的⑭_____倍． 第 8 页 2　 § (3)三角形的高线． § 从三角形一个顶点向它的对边作一条垂线， 顶点和垂足之间的线段叫做三角形这条边上 的⑮______. 第 9 页 高　 第 10 页 垂心　 内部　 内部　 直角边　 内部　 外部　 第 11 页 中点　 平行　 一半　 第 12 页 § (5)三角形的中垂线． § 三角形的边的中垂线有时也叫三角形的中垂 线．三角形中垂线的交点是三角形的外心， 三角形的外心到三角形三个顶点的距离相 等． 第 13 页 方法点拨：如图，三角形都有三条中垂线．锐角三角形的三条中垂线交于三 角形内部一点，即外心在三角形内部；直角三角形的三条中垂线交于斜边中点处， 即外心在斜边中点处；钝角三角形的三条中垂线交于三角形外部一点，即外心在三 角形外部． 第 14 页 § 1．三角形的稳定性 § 定义：如果三角形三边的长度固定，那么三 角形的形状和大小就能唯一确定．三角形的 这个性质叫做三角形的稳定性． § 应用：三角形的稳定性是三角形独有的性质， 在现实生活中应用非常广泛．如：大桥的钢 架做成三角形、高压电线的支架做成三角形 等． 第 15 页 方法点拨：由于四边形具有不稳定性，常通过改造将其变成三角形，从而使 其稳定． 第 16 页 大于　 小于　 方法点拨：三角形的三边关系一般有两个应用：(1)判定所给的三条线段能否 构成三角形；(2)已知三角形的两边长，求第三边的取值范围． 第 17 页 180°　 180°　 等于　 大于　 第 18 页 360°　 大角　 小角　 方法点拨：三角形的内角和定理与三角形外角的性质是求角的度数和证明角 之间的关系常用的依据． 第 19 页 第 20 页 (n－2)×180°　 360°　 第 21 页 (n－3)　 (n－2)　 第 22 页 相等　 相等　 相等　 相等　 相等　 第 23 页 轴对称　 n　 中心对称　 轴对称　 n　 § 命题点一　三角形中的边、角关系 § 1．(2019·自贡中考)已知三角形的两边长分 别为1和4，第三边长为整数，则该三角形的 周长为 (　　) § A．7　 B．8　 § C．9　 D．10 第 24 页 C　 § 2．(2018·眉山中考)将一副直角三角板按如 图所示的位置放置，使含30°角的三角板的 一条直角边和含45°角的三角板的一条直角 边放在同一条直线上，则∠α的度数是 (　　) § A．45°　 § B．60°　 § C．75°　 § D．85° 第 25 页 C　 第 26 页 第 27 页 40°　 9　 § 命题点二　三角形中的重要线段 § 6．(2019·眉山中考)如图，在△ABC中，AD 平分∠BAC交BC于点D，∠B＝30°， ∠ADC＝70°，则∠C的度数是 (　　) § A．50°　 § B．60°　 § C．70°　 § D．80° 第 28 页 C　 § 7．(2017·眉山中考)如图，在△ABC中， ∠A＝66°，点I是内心，则∠BIC的大小为 (　　) § A．114°　 § B．122°　 § C．123°　 § D．132° 第 29 页 C　 § 8．(2016·乐山中考)如图，CE是△ABC的外 角∠ACD的平分线，若∠B＝35°，∠ACE ＝60°，则∠A＝ (　　) § A．35°　 B．95°　 § C．85°　 D．75° 第 30 页 C　 § 9．(2018·南充中考)如图，在△ABC中，AF 平分∠BAC，AC的垂直平分线交BC于点E， ∠B＝70°，∠FAE＝19°，则∠C＝ ______度． 第 31 页 24　 § 10．(2017·泸州中考)在△ABC中，已知BD和CE分别是边AC、 AB上的中线，且BD⊥CE，垂足为O.若OD＝2 cm，OE＝4 cm， 则线段AO的长度为_______cm. § 11．(2018·巴中中考)如图，在△ABC中，BO、CO分别平分 ∠ABC、∠ACB．若∠BOC＝110°，则∠A＝________. 第 32 页 40°　 § 12．(2019·攀枝花中考)如图，在△ABC中， CD是AB边上的高，BE是AC边上的中线，且 BD＝CE.求证： § (1)点D在BE的垂直平分线上； § (2)∠BEC＝3∠ABE. 第 33 页 § 证明：(1)连结DE.∵CD是AB边上的高， ∴∠ADC＝∠BDC＝90°.∵BE是△ABC中 BC边上的中线，∴DE是Rt△ADC斜边AC上 的中线，∴DE＝AE＝CE.∵BD＝CE，∴BD ＝DE，∴点D在BE的垂直平分线上． § (2)∵DE＝AE，∴∠A＝∠ADE.∵BD＝DE， ∴∠DBE＝∠DEB．∵∠ADE＝∠DBE＋ ∠DEB，∴∠A＝∠ADE＝ 2∠ABE.∵∠BEC＝∠A＋∠ABE， ∴∠BEC＝3∠ABE. 第 34 页 § 命题点三　多边形及其性质 § 13．(2019·德阳中考)若一个多边形的内角 和为其外角和的2倍，则这个多边形为 (　　) § A．六边形　 B．八边形 § C．十边形　 D．十二边形 § 14．(2019·广安中考)如图，正五边形 ABCDE中，对角线AC与BE相交于点F，则 ∠AFE＝______度． 第 35 页 A　 72　 § 15．(2019·宜宾中考)如图，六边形 ABCDEF的内角都相等，AD∥BC，则 ∠DAB＝________. § 16．(2019·资阳中考)若正多边形的一个外 角是60°，则这个正多边形的内角和是 _________. § 17．(2018·广安中考)一个n边形的每一个内 角都等于108°，那么n＝_____. § 18．(2018·广元中考)一个多边形的每一个 外角都是18°，这个多边形的边数为______. 第 36 页 60°　 720°　 5　 20　 § 19．(2016·攀枝花中考)如果一个正多边形 的每个外角都是30°，那么这个多边形的内 角和为__________. § 20．(2016·资阳中考)如图，AC是正五边形 ABCDE的一条对角线，则∠ACB＝ ________. 第 37 页 1800°　 36°　 § 21．(2017·资阳中考)边长相等的正五边形 与正六边形按如图所示拼接在一起，则 ∠ABC＝______度． 第 38 页 24　 § 核心素养 § 22．(2019·山东枣庄中考)将一副直角三角 板按如图所示的位置放置，使含30°角的三 角板的一条直角边和含45°角的三角板的一 条直角边放在同一条直线上，则∠α的度数 是 (　　) § A．45°　 § B．60°　 § C．75°　 § D．85° 第 39 页 C　 § 23．(2019·广东广州中考)一副三角板如图 放置，将三角板ADE绕点A逆时针旋转α(0° ＜α＜90°)，使得三角板ADE的一边所在的 直线与BC垂直，则α的度数为 ______________. 第 40 页 15°或60°　 § 24．(2019·山东枣庄中考)用一条宽度相等 的足够长的纸条打一个结(如图1所示)，然后 轻轻拉紧、压平就可以得到如图2所示的正五 边形ABCDE.图中，∠BAC＝________. 第 41 页 36°　 图1 图2 § 突破点一　三角形的三边关系 § 　　　(江苏泰州中考)已知三角形两边的长 分别为1、5，第三边长为整数，则第三边的 长为_____. § 思路分析：已知三角形两边的长分别为1、5， 根据三角形的三边关系“任意两边之和＞第 三边，任意两边之差＜第三边”，得5－1< 第三边＜1＋5，即4<第三边<6.又第三边长 为整数，故第三边的长为5. 第 42 页 5　 § 突破点二　三角形中重要线段的相关计算 § 　　　(吉林长春中考)如图，在△ABC中，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E.若∠A＝54°，∠B＝48°， 则∠CDE的大小为 (　　) § A．44°　 § B．40°　 § C．39°　 § D．38° 第 43 页 C　 § 　　　(2019·黑龙江大庆中考)如图，在 △ABC中，D、E分别是BC、AC的中点， AD与BE相交于点G，若DG＝1，则AD＝ _____. § 思路分析：∵D、E分别是BC、AC的中点， ∴点G为△ABC的重心，∴AG＝2DG＝2， ∴AD＝AG＋DG＝2＋1＝3.故答案为3. § 解题技巧：本题考查了三角形重心的性质： 重心到顶点的距离与重心到对边中点的距离 之比为2∶1. 第 44 页 3　 § 突破点三　三角形的外角性质 § 　　　(山东聊城中考)如图，将一张三角形 纸片ABC的一角折叠，使点A落在△ABC外 的A′处，折痕为DE.如果∠A＝α，∠CEA′＝ β，∠BDA′＝γ，那么下列式子中正确的是 (　　) § A．γ＝2α＋β　 § B．γ＝α＋2β § C．γ＝α＋β　 § D．γ＝180°－α－β 第 45 页 A　 § 思路分析：由折叠，得∠A′＝∠A．根据三角 形的外角的性质，得∠BDA′＝∠A＋∠AFD， ∠AFD＝∠A′＋∠CEA′.∵∠A＝α，∠CEA′ ＝β，∠BDA′＝γ，∴∠BDA′＝γ＝α＋α＋β ＝2α＋β. § 解题技巧：掌握三角形的一个外角等于和它 不相邻的两个内角的和是解题的关键． 第 46 页 § 突破点四　多边形的内、外角和定理 § 　　　(2019·山东莱芜中考)如果一个多边形 的内角和是外角和的5倍，那么这个多边形的 边数是 (　　) § A．10　 B．11　 § C．12　 D．13 § 思路分析：设这个多边形是n边形，根据题意， 得(n－2)·180°＝5×360°，解得n＝12.故 选C． § 解题技巧：根据多边形的内角和公式(n－ 2)·180°与外角和定理列出方程，然后求解 即可． 第 47 页 C　 § 1．(2019·江苏扬州中考)已知n是正整数， 若一个三角形的3边长分别是n＋2、n＋8、 3n，则满足条件的n的值有 (　　) § A．4个　 B．5个　 § C．6个　 D．7个 第 48 页 A 双基过关 D　 § 2．(2019·山东青岛中考)如图，BD是△ABC 的角平分线，AE⊥BD，垂足为F.若∠ABC ＝35°，∠C＝50°，则∠CDE的度数为 (　　) § A．35°　 B．40°　 § C．45°　 D．50° 第 49 页 C　 第 50 页 C　 § 4．(2019·湖北咸宁中考)若正多边形的内角 和是540°，则该正多边形的一个外角为 (　　) § A．45°　 B．60°　 § C．72°　 D．90° § 5．(2018·广西中考)如图，∠ACD是△ABC 的外角，CE平分∠ACD，若∠A＝60°， ∠B＝40°，则∠ECD等于 (　　) § A．40°　 § B．45°　 § C．50°　 § D．55° 第 51 页 C　 C　 § 6．(湖北黄石中考)如图，△ABC中，AD是 BC边上的高，AE、BF分别是∠BAC、 ∠ABC的平分线，∠BAC＝50°，∠ABC＝ 60°，则∠EAD＋∠ACD＝ (　　) § A．75°　 § B．80°　 § C．85°　 § D．90° 第 52 页 A　 § 7．(黑龙江大庆中考)如图，∠B＝∠C＝ 90°，M是BC的中点，DM平分∠ADC，且 ∠ADC＝110°，则∠MAB＝ (　　) § A．30°　 § B．35°　 § C．45°　 § D．60° 第 53 页 B　 § 8．(湖南邵阳中考)如图所示，在四边形 ABCD中，AD⊥AB，∠C＝110°，它的一 个外角∠ADE＝60°，则∠B的大小是 ________． 第 54 页 40°　 § 9．(江苏南京中考)如图，五边形ABCDE是 正五边形．若l1∥l2，则∠1－∠2＝ ________． 第 55 页 72°　 § 10．(湖北宜昌中考)如图，在Rt△ABC中，∠ACB＝90°，∠A＝40°，△ABC的外角∠CBD的平 分线BE交AC的延长线于点E． § (1)求∠CBE的度数； § (2)过点D作DF∥BE，交AC的延长线于点F，求 ∠F的度数． 第 56 页 第 57 页 B 满分过关 第 58 页 D　 § 13．(山东聊城中考)如果一个正方形被截掉 一个角后，得到一个多边形，那么这个多边 形的内角和是 _______________________． § 14．(甘肃白银中考)已知a、b、c是△ABC的 三边长，a、b满足|a－7|＋(b－1)2＝0，c为 奇数，则c＝_____． § 15．(四川广安中考)若一个正n边形的每个内 角为144°，则这个正n边形的所有对角线的 条数是______． 第 59 页 540°或360°或180°　 7　 35　 § 16．(四川广元模拟)如图1所示，圆上均匀分 布着A1、A2、A3、…、A1111个点．从A1起每 隔k个点顺次连结，当再次与点A1连结时，我 们把所形成的图形称为“k＋1阶正十一角 星”，其中1≤k≤8(k为正整数)．如：图2是 “2阶正十一角星”，那么∠A1＋∠A2＋… ＋∠A11＝__________；当∠A1＋∠A2＋… ＋∠A11＝900°时，k＝________． 第 60 页 1260°　 2或7　 § 17．(四川成都模拟)如图，△ABC中，∠A＝96°，D是BC延长 线上的一点，∠ABC与∠ACD(△ACB的外角)的平分线交于点A1， 则∠A1＝______度；如果∠A＝α，按以上的方法依次作出 ∠BA2C、∠BA3C、…、∠BAnC(n为正整数)，则∠An 第 61 页 48　 ＝________度(用含α的代数式表示)． § 18．(四川南充模拟)四边形是大家最熟悉的图形之一，我们已经发现了 它的许多性质．只要善于观察、乐于探索，我们还会发现更多的结论． 第 62 页 § (1)四边形一条对角线上任意一点与另外两个 顶点的连线，将四边形分成四个三角形(如图 1)，其中相对的两对三角形的面积之积相 等．你能证明这个结论吗？已知：在四边形 ABCD中，O是对角线BD上任意一点，如图1. 求证：S△OBC·S△OAD＝S△OAB·S△OCD； § (2)在三角形中(如图2)，你能否归纳出类似的 结论？若能，写出你猜想的结论，并证明： 若不能，说明理由． 第 63 页 第 64 页 第 65 页