2019年四川省绵阳市中考数学试卷含答案 34页

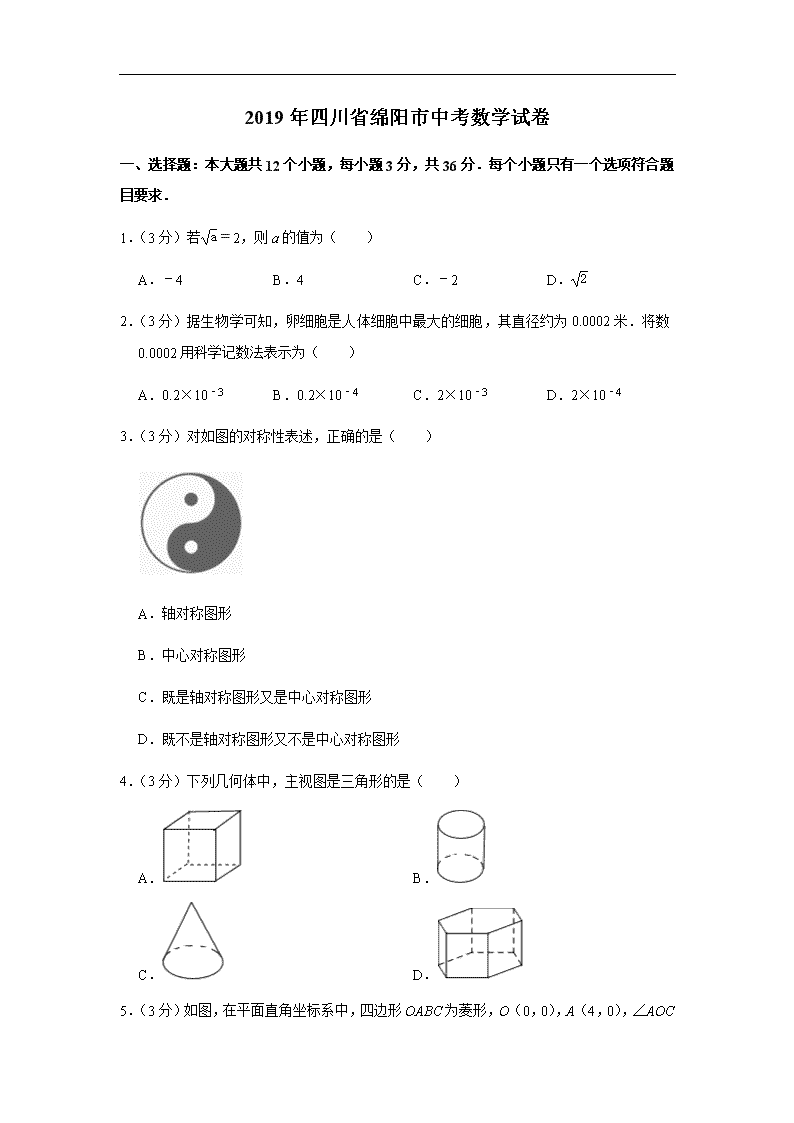
‎2019年四川省绵阳市中考数学试卷 一、选择题：本大题共12个小题，每小题3分，共36分．每个小题只有一个选项符合题目要求．‎ ‎1．（3分）若a‎=‎2，则a的值为（　　）‎ A．﹣4 B．4 C．﹣2 D．‎‎2‎ ‎2．（3分）据生物学可知，卵细胞是人体细胞中最大的细胞，其直径约为0.0002米．将数0.0002用科学记数法表示为（　　）‎ A．0.2×10﹣3 B．0.2×10﹣4 C．2×10﹣3 D．2×10﹣4‎ ‎3．（3分）对如图的对称性表述，正确的是（　　）‎ A．轴对称图形 ‎ B．中心对称图形 ‎ C．既是轴对称图形又是中心对称图形 ‎ D．既不是轴对称图形又不是中心对称图形 ‎4．（3分）下列几何体中，主视图是三角形的是（　　）‎ A． B． ‎ C． D．‎ ‎5．（3分）如图，在平面直角坐标系中，四边形OABC为菱形，O（0，0），A（4，0），∠AOC ‎＝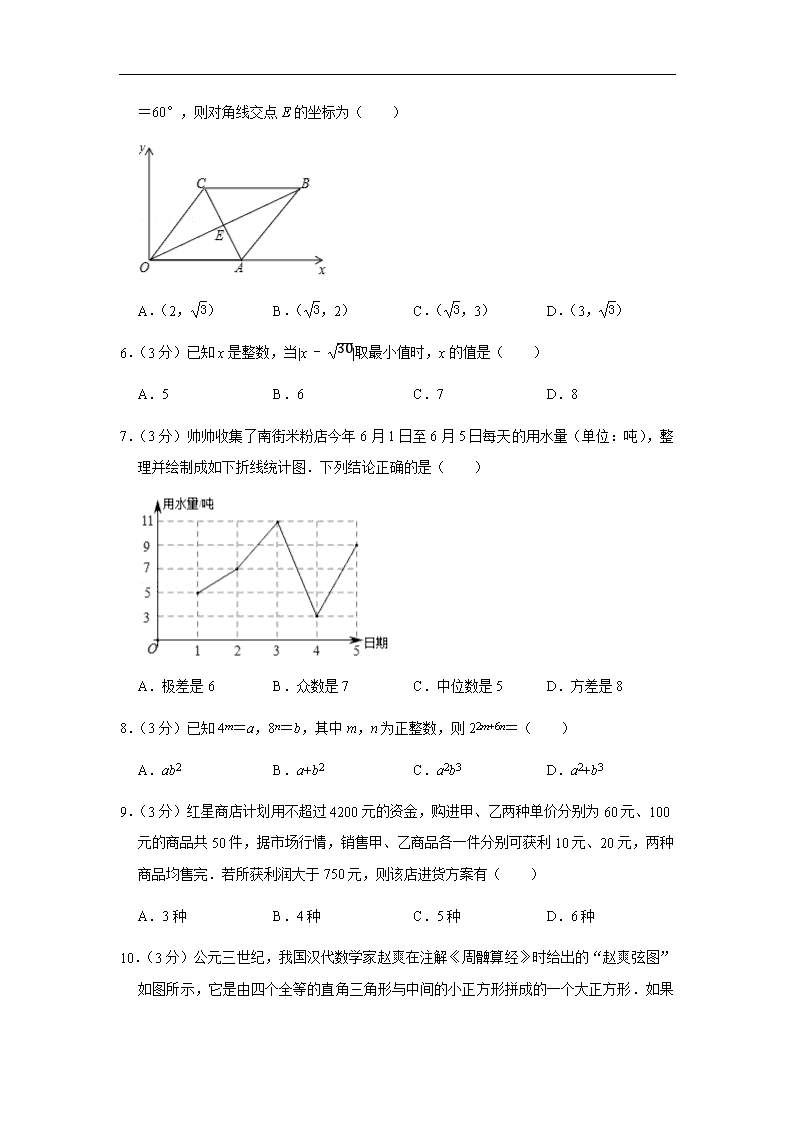60°，则对角线交点E的坐标为（　　）‎ A．（2，‎3‎） B．（‎3‎，2） C．（‎3‎，3） D．（3，‎3‎）‎ ‎6．（3分）已知x是整数，当|x‎-‎‎30‎|取最小值时，x的值是（　　）‎ A．5 B．6 C．7 D．8‎ ‎7．（3分）帅帅收集了南街米粉店今年6月1日至6月5日每天的用水量（单位：吨），整理并绘制成如下折线统计图．下列结论正确的是（　　）‎ A．极差是6 B．众数是7 C．中位数是5 D．方差是8‎ ‎8．（3分）已知4m＝a，8n＝b，其中m，n为正整数，则22m+6n＝（　　）‎ A．ab2 B．a+b2 C．a2b3 D．a2+b3‎ ‎9．（3分）红星商店计划用不超过4200元的资金，购进甲、乙两种单价分别为60元、100元的商品共50件，据市场行情，销售甲、乙商品各一件分别可获利10元、20元，两种商品均售完．若所获利润大于750元，则该店进货方案有（　　）‎ A．3种 B．4种 C．5种 D．6种 ‎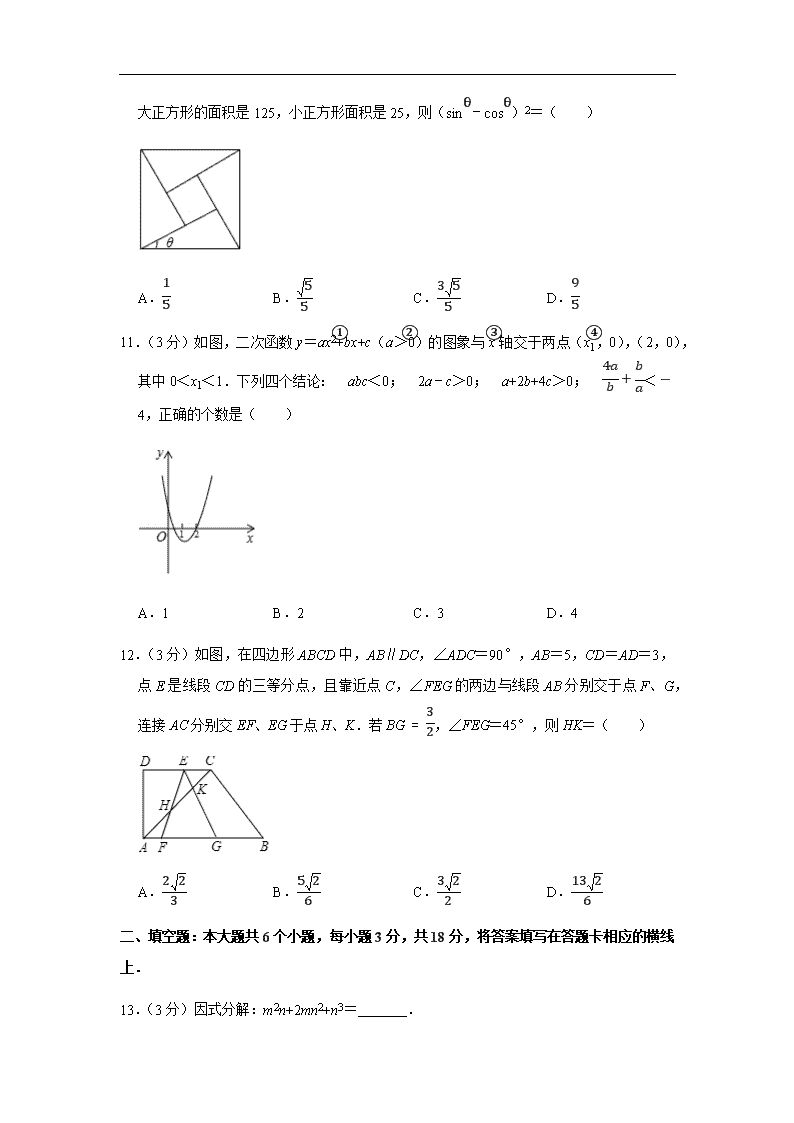10．（3分）公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形的面积是125，小正方形面积是25，则（sinθ﹣cosθ）2＝（　　）‎ A．‎1‎‎5‎ B．‎5‎‎5‎ C．‎3‎‎5‎‎5‎ D．‎‎9‎‎5‎ ‎11．（3分）如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于两点（x1，0），（2，0），其中0＜x1＜1．下列四个结论：①abc＜0；②2a﹣c＞0；③a+2b+4c＞0；④‎4ab‎+ba＜-‎4，正确的个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎12．（3分）如图，在四边形ABCD中，AB∥DC，∠ADC＝90°，AB＝5，CD＝AD＝3，点E是线段CD的三等分点，且靠近点C，∠FEG的两边与线段AB分别交于点F、G，连接AC分别交EF、EG于点H、K．若BG‎=‎‎3‎‎2‎，∠FEG＝45°，则HK＝（　　）‎ A．‎2‎‎2‎‎3‎ B．‎5‎‎2‎‎6‎ C．‎3‎‎2‎‎2‎ D．‎‎13‎‎2‎‎6‎ 二、填空题：本大题共6个小题，每小题3分，共18分，将答案填写在答题卡相应的横线上．‎ ‎13．（3分）因式分解：m2n+2mn2+n3＝　 　．‎ ‎14．（3分）如图，AB∥CD，∠ABD的平分线与∠BDC的平分线交于点E，则∠1+∠2＝　 　．‎ ‎15．（3分）单项式x﹣|a﹣1|y与2xb-1‎y是同类项，则ab＝　 　．‎ ‎16．（3分）一艘轮船在静水中的最大航速为30km/h，它以最大航速沿江顺流航行120km所用时间，与以最大航速逆流航行60km所用时间相同，则江水的流速为　 　km/h．‎ ‎17．（3分）在△ABC中，若∠B＝45°，AB＝10‎2‎，AC＝5‎5‎，则△ABC的面积是　 　．‎ ‎18．（3分）如图，△ABC、△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝2‎2‎．将△BDE绕点B逆时针方向旋转后得△BD′E′，当点E′恰好落在线段AD′上时，则CE′＝　 　．‎ 三、解答题：本大题共7个小题，共86分，解答应写出文字说明、证明过程或演算步骤 ‎19．（16分）（1）计算：2‎2‎‎3‎‎+‎|（‎-‎‎1‎‎2‎）﹣1|﹣2‎2‎tan30°﹣（π﹣2019）0；‎ ‎（2）先化简，再求值：（aa‎2‎‎-‎b‎2‎‎-‎‎1‎a+b）‎÷‎bb-a，其中a‎=‎‎2‎，b＝2‎-‎‎2‎．‎ ‎20．（11分）胜利中学为丰富同学们的校园生活，举行“校园电视台主待人“选拔赛，现将36名参赛选手的成绩（单位：分）统计并绘制成频数分布直方图和扇形统计图，部分信息如下：‎ 请根据统计图的信息，解答下列问题：‎ ‎（1）补全频数分布直方图，并求扇形统计图中扇形D对应的圆心角度数；‎ ‎（2）成绩在D区域的选手，男生比女生多一人，从中随机抽取两人临时担任该校艺术节的主持人，求恰好选中一名男生和一名女生的概率．‎ ‎21．（11分）辰星旅游度假村有甲种风格客房15间，乙种风格客房20间．按现有定价：若全部入住，一天营业额为8500元；若甲、乙两种风格客房均有10间入住，一天营业额为5000元．‎ ‎（1）求甲、乙两种客房每间现有定价分别是多少元？‎ ‎（2）度假村以乙种风格客房为例，市场情况调研发现：若每个房间每天按现有定价，房间会全部住满；当每个房间每天的定价每增加20元时，就会有两个房间空闲．如果游客居住房间，度假村需对每个房间每天支出80元的各种费用．当每间房间定价为多少元时，乙种风格客房每天的利润m最大，最大利润是多少元？‎ ‎22．（11分）如图，一次函数y＝kx+b（k≠0）的图象与反比例函数y‎=‎m‎2‎‎-3mx（m≠0且m≠3）的图象在第一象限交于点A、B，且该一次函数的图象与y轴正半轴交于点C，过A、B分别作y轴的垂线，垂足分别为E、D．已知A（4，1），CE＝4CD．‎ ‎（1）求m的值和反比例函数的解析式；‎ ‎（2）若点M为一次函数图象上的动点，求OM长度的最小值．‎ ‎23．（11分）如图，AB是⊙O的直径，点C为BD的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．‎ ‎（1）求证：△BFG≌△CDG；‎ ‎（2）若AD＝BE＝2，求BF的长．‎ ‎24．（12分）在平面直角坐标系中，将二次函数y＝ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x轴交于点A、B（点A在点B的左侧），OA＝1，经过点A的一次函数y＝kx+b（k≠0）的图象与y轴正半轴交于点C，且与抛物线的另一个交点为D，△ABD的面积为5．‎ ‎（1）求抛物线和一次函数的解析式；‎ ‎（2）抛物线上的动点E在一次函数的图象下方，求△ACE面积的最大值，并求出此时点E的坐标；‎ ‎（3）若点P为x轴上任意一点，在（2）的结论下，求PE‎+‎‎3‎‎5‎PA的最小值．‎ ‎25．（14分）如图，在以点O为中心的正方形ABCD中，AD＝4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．‎ ‎（1）求证：△DEF是等腰直角三角形；‎ ‎（2）当点H恰好落在线段BC上时，求EH的长；‎ ‎（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．‎ ‎2019年四川省绵阳市中考数学试卷 参考答案与试题解析 一、选择题：本大题共12个小题，每小题3分，共36分．每个小题只有一个选项符合题目要求．‎ ‎1．（3分）若a‎=‎2，则a的值为（　　）‎ A．﹣4 B．4 C．﹣2 D．‎‎2‎ ‎【解答】解：若a‎=‎2，则a＝4，‎ 故选：B．‎ ‎2．（3分）据生物学可知，卵细胞是人体细胞中最大的细胞，其直径约为0.0002米．将数0.0002用科学记数法表示为（　　）‎ A．0.2×10﹣3 B．0.2×10﹣4 C．2×10﹣3 D．2×10﹣4‎ ‎【解答】解：将数0.0002用科学记数法表示为2×10﹣4，‎ 故选：D．‎ ‎3．（3分）对如图的对称性表述，正确的是（　　）‎ A．轴对称图形 ‎ B．中心对称图形 ‎ C．既是轴对称图形又是中心对称图形 ‎ D．既不是轴对称图形又不是中心对称图形 ‎【解答】解：如图所示：是中心对称图形．‎ 故选：B．‎ ‎4．（3分）下列几何体中，主视图是三角形的是（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：A、正方体的主视图是正方形，故此选项错误；‎ B、圆柱的主视图是长方形，故此选项错误；‎ C、圆锥的主视图是三角形，故此选项正确；‎ D、六棱柱的主视图是长方形，中间还有两条竖线，故此选项错误；‎ 故选：C．‎ ‎5．（3分）如图，在平面直角坐标系中，四边形OABC为菱形，O（0，0），A（4，0），∠AOC＝60°，则对角线交点E的坐标为（　　）‎ A．（2，‎3‎） B．（‎3‎，2） C．（‎3‎，3） D．（3，‎3‎）‎ ‎【解答】解：过点E作EF⊥x轴于点F，‎ ‎∵四边形OABC为菱形，∠AOC＝60°，‎ ‎∴‎∠AOE=‎1‎‎2‎∠AOC=‎30°，∠FAE＝60°，‎ ‎∵A（4，0），‎ ‎∴OA＝4，‎ ‎∴AE=‎1‎‎2‎AO=‎1‎‎2‎×4=‎2，‎ ‎∴AF=‎1‎‎2‎AE=1‎，EF‎=AE‎2‎-AF‎2‎=‎2‎‎2‎‎-‎‎1‎‎2‎=‎‎3‎，‎ ‎∴OF＝AO﹣AF＝4﹣1＝3，‎ ‎∴E(3，‎3‎)‎．‎ 故选：D．‎ ‎6．（3分）已知x是整数，当|x‎-‎‎30‎|取最小值时，x的值是（　　）‎ A．5 B．6 C．7 D．8‎ ‎【解答】解：∵‎25‎‎＜‎30‎＜‎‎36‎，‎ ‎∴5‎＜‎30‎＜6‎，‎ 且与‎30‎最接近的整数是5，‎ ‎∴当|x‎-‎‎30‎|取最小值时，x的值是5，‎ 故选：A．‎ ‎7．（3分）帅帅收集了南街米粉店今年6月1日至6月5日每天的用水量（单位：吨），整理并绘制成如下折线统计图．下列结论正确的是（　　）‎ A．极差是6 B．众数是7 C．中位数是5 D．方差是8‎ ‎【解答】解：由图可知，6月1日至6月5日每天的用水量是：5，7，11，3，9．‎ A．极差＝11﹣3＝8，结论错误，故A不符合题意；‎ B．众数为5，7，11，3，9，结论错误，故B不符合题意；‎ C．这5个数按从小到大的顺序排列为：3，5，7，9，11，中位数为7，结论错误，故C不符合题意；‎ D．平均数是（5+7+11+3+9）÷5＝7，‎ 方差S2‎=‎‎1‎‎5‎[（5﹣7）2+（7﹣7）2+（11﹣7）2+（3﹣7）2+（9﹣7）2]＝8．‎ 结论正确，故D符合题意；‎ 故选：D．‎ ‎8．（3分）已知4m＝a，8n＝b，其中m，n为正整数，则22m+6n＝（　　）‎ A．ab2 B．a+b2 C．a2b3 D．a2+b3‎ ‎【解答】解：∵4m＝a，8n＝b，‎ ‎∴22m+6n＝22m×26n ‎＝（22）m•（23）2n ‎＝4m•82n ‎＝4m•（8n）2‎ ‎＝ab2，‎ 故选：A．‎ ‎9．（3分）红星商店计划用不超过4200元的资金，购进甲、乙两种单价分别为60元、100元的商品共50件，据市场行情，销售甲、乙商品各一件分别可获利10元、20元，两种商品均售完．若所获利润大于750元，则该店进货方案有（　　）‎ A．3种 B．4种 C．5种 D．6种 ‎【解答】解：设该店购进甲种商品x件，则购进乙种商品（50﹣x）件，‎ 根据题意，得：‎60x+100(50-x)≤4200‎‎10x+20(50-x)＞750‎，‎ 解得：20≤x＜25，‎ ‎∵x为整数，‎ ‎∴x＝20、21、22、23、24，‎ ‎∴该店进货方案有5种，‎ 故选：C．‎ ‎10．（3分）公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形的面积是125，小正方形面积是25，则（sinθ﹣cosθ）2＝（　　）‎ A．‎1‎‎5‎ B．‎5‎‎5‎ C．‎3‎‎5‎‎5‎ D．‎‎9‎‎5‎ ‎【解答】解：∵大正方形的面积是125，小正方形面积是25，‎ ‎∴大正方形的边长为5‎5‎，小正方形的边长为5，‎ ‎∴5‎5‎cosθ﹣5‎5‎sinθ＝5，‎ ‎∴cosθ﹣sinθ‎=‎‎5‎‎5‎，‎ ‎∴（sinθ﹣cosθ）2‎=‎‎1‎‎5‎．‎ 故选：A．‎ ‎11．（3分）如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于两点（x1，0），（2，0），其中0＜x1＜1．下列四个结论：①abc＜0；②2a﹣c＞0；③a+2b+4c＞0；④‎4ab‎+ba＜-‎4，正确的个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎【解答】解：①∵抛物线开口向上，‎ ‎∴a＞0，‎ ‎∵抛物线对称轴在y轴的右侧，‎ ‎∴b＜0，‎ ‎∵抛物线与y轴的交点在x轴上方，‎ ‎∴c＞0，‎ ‎∴abc＜0，所以①正确；‎ ‎②∵图象与x轴交于两点（x1，0），（2，0），其中0＜x1＜1，‎ ‎∴‎2+0‎‎2‎‎＜-b‎2a＜‎‎2+1‎‎2‎，‎ ‎∴1‎＜-b‎2a＜‎‎3‎‎2‎，‎ 当‎-b‎2a＜‎‎3‎‎2‎时，b＞﹣3a，‎ ‎∵当x＝2时，y＝4a+2b+c＝0，‎ ‎∴b＝﹣2a‎-‎‎1‎‎2‎c，‎ ‎∴﹣2a‎-‎‎1‎‎2‎c＞﹣3a，‎ ‎∴2a﹣c＞0，故②正确；‎ ‎③当x‎=‎‎1‎‎2‎时，y的值为‎1‎‎4‎a‎+‎‎1‎‎2‎b+c，‎ 给‎1‎‎4‎a‎+‎‎1‎‎2‎b+c乘以4，即可化为a+2b+4c，‎ ‎∵抛物线的对称轴在1‎＜-b‎2a＜‎‎3‎‎2‎，‎ ‎∴x‎=‎‎1‎‎2‎关于对称轴对称点的横坐标在‎3‎‎2‎和‎5‎‎2‎之间，‎ 由图象可知在‎3‎‎2‎和2之间y为负值，2和‎5‎‎2‎之间y为正值，‎ ‎∴a+2b+4c与0的关系不能确定，‎ 故③错误；‎ ‎④∵‎-b‎2a＞1‎，‎ ‎∴2a+b＜0，‎ ‎∴（2a+b）2＞0，‎ ‎4a2+b2+4ab＞0，‎ ‎4a2+b2＞﹣4ab，‎ ‎∵a＞0，b＜0，‎ ‎∴ab＜0，‎ ‎∴‎4a‎2‎+‎b‎2‎ab‎＜-4‎，‎ 即‎4ab‎+ba＜-4‎，‎ 故④正确．‎ 故选：C．‎ ‎12．（3分）如图，在四边形ABCD中，AB∥DC，∠ADC＝90°，AB＝5，CD＝AD＝3，点E是线段CD的三等分点，且靠近点C，∠FEG的两边与线段AB分别交于点F、G，连接AC分别交EF、EG于点H、K．若BG‎=‎‎3‎‎2‎，∠FEG＝45°，则HK＝（　　）‎ A．‎2‎‎2‎‎3‎ B．‎5‎‎2‎‎6‎ C．‎3‎‎2‎‎2‎ D．‎‎13‎‎2‎‎6‎ ‎【解答】解：∵∠ADC＝90°，CD＝AD＝3，‎ ‎∴AC＝3‎2‎，‎ ‎∵AB＝5，BG‎=‎‎3‎‎2‎，‎ ‎∴AG‎=‎‎7‎‎2‎，‎ ‎∵AB∥DC，‎ ‎∴△CEK∽△AGK，‎ ‎∴CEAG‎=CKAK=‎EKKG，‎ ‎∴‎1‎‎7‎‎2‎‎=CKAK=‎EKKG，‎ ‎∴CKAK‎=EKKG=‎‎2‎‎7‎，‎ ‎∵CK+AK＝3‎2‎，‎ ‎∴CK‎=‎‎2‎‎2‎‎3‎，‎ 过E作EM⊥AB于M，‎ 则四边形ADEM是矩形，‎ ‎∴EM＝AD＝3，AM＝DE＝2，‎ ‎∴MG‎=‎‎3‎‎2‎，‎ ‎∴EG‎=EM‎2‎+MG‎2‎=‎‎3‎‎5‎‎2‎，‎ ‎∵EKKG‎=‎‎2‎‎7‎，‎ ‎∴EK‎=‎‎5‎‎3‎，‎ ‎∵∠HEK＝∠KCE＝45°，∠EHK＝∠CHE，‎ ‎∴△HEK∽△HCE，‎ ‎∴HEHK‎=‎1‎‎5‎‎3‎=‎‎3‎‎5‎，‎ ‎∴设HE＝3x，HK‎=‎‎5‎x，‎ ‎∵△HEK∽△HCE，‎ ‎∴EHHC‎=‎HKEH，‎ ‎∴‎3x‎5‎x+‎‎2‎‎2‎‎3‎‎=‎‎5‎x‎3x，‎ 解得：x‎=‎‎10‎‎6‎，‎ ‎∴HK‎=‎‎5‎‎2‎‎6‎，‎ 故选：B．‎ 二、填空题：本大题共6个小题，每小题3分，共18分，将答案填写在答题卡相应的横线上．‎ ‎13．（3分）因式分解：m2n+2mn2+n3＝　n（m+n）2　．‎ ‎【解答】解：m2n+2mn2+n3‎ ‎＝n（m2+2mn+n2）‎ ‎＝n（m+n）2．‎ 故答案为：n（m+n）2．‎ ‎14．（3分）如图，AB∥CD，∠ABD的平分线与∠BDC的平分线交于点E，则∠1+∠2＝　90°　．‎ ‎【解答】解：∵AB∥CD，‎ ‎∴∠ABD+∠CDB＝180°，‎ ‎∵BE是∠ABD的平分线，‎ ‎∴∠1‎=‎‎1‎‎2‎∠ABD，‎ ‎∵BE是∠BDC的平分线，‎ ‎∴∠2‎=‎‎1‎‎2‎∠CDB，‎ ‎∴∠1+∠2＝90°，‎ 故答案为：90°．‎ ‎15．（3分）单项式x﹣|a﹣1|y与2xb-1‎y是同类项，则ab＝　1　．‎ ‎【解答】解：由题意知﹣|a﹣1|‎=b-1‎≥‎0，‎ ‎∴a＝1，b＝1，‎ 则ab＝（1）1＝1，‎ 故答案为：1．‎ ‎16．（3分）一艘轮船在静水中的最大航速为30km/h，它以最大航速沿江顺流航行120km所用时间，与以最大航速逆流航行60km所用时间相同，则江水的流速为　10　km/h．‎ ‎【解答】解：设江水的流速为xkm/h，根据题意可得：‎ ‎120‎‎30+x‎=‎‎60‎‎30-x‎，‎ 解得：x＝10，‎ 经检验得：x＝10是原方程的根，‎ 答：江水的流速为10km/h．‎ 故答案为：10．‎ ‎17．（3分）在△ABC中，若∠B＝45°，AB＝10‎2‎，AC＝5‎5‎，则△ABC的面积是　75或25　．‎ ‎【解答】解：过点A作AD⊥BC，垂足为D，如图所示．‎ 在Rt△ABD中，AD＝AB•sinB＝10，BD＝AB•cosB＝10；‎ 在Rt△ACD中，AD＝10，AC＝5‎5‎，‎ ‎∴CD‎=AC‎2‎-AD‎2‎=‎5，‎ ‎∴BC＝BD+CD＝15或BC＝BD﹣CD＝5，‎ ‎∴S△ABC‎=‎‎1‎‎2‎BC•AD＝75或25．‎ 故答案为：75或25．‎ ‎18．（3分）如图，△ABC、△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝2‎2‎．将△BDE绕点B逆时针方向旋转后得△BD′E′，当点E′恰好落在线段AD′上时，则CE′＝　‎2‎‎+‎‎6‎　．‎ ‎【解答】解：如图，连接CE′，‎ ‎∵△ABC、△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝2‎2‎，‎ ‎∴AB＝BC＝2‎2‎，BD＝BE＝2，‎ ‎∵将△BDE绕点B逆时针方向旋转后得△BD′E′，‎ ‎∴D′B＝BE′＝BD＝2，∠D′BE′＝90′，∠D′BD＝∠ABE′，‎ ‎∴∠ABD′＝∠CBE′，‎ ‎∴△ABD′≌△CBE′（SAS），‎ ‎∴∠D′＝∠CE′B＝45°，‎ 过B作BH⊥CE′于H，‎ 在Rt△BHE′中，BH＝E′H‎=‎‎2‎‎2‎BE′‎=‎‎2‎，‎ 在Rt△BCH中，CH‎=BC‎2‎-BH‎2‎=‎‎6‎，‎ ‎∴CE′‎=‎2‎+‎‎6‎，‎ 故答案为：‎2‎‎+‎‎6‎．‎ 三、解答题：本大题共7个小题，共86分，解答应写出文字说明、证明过程或演算步骤 ‎19．（16分）（1）计算：2‎2‎‎3‎‎+‎|（‎-‎‎1‎‎2‎）﹣1|﹣2‎2‎tan30°﹣（π﹣2019）0；‎ ‎（2）先化简，再求值：（aa‎2‎‎-‎b‎2‎‎-‎‎1‎a+b）‎÷‎bb-a，其中a‎=‎‎2‎，b＝2‎-‎‎2‎．‎ ‎【解答】解：（1）2‎2‎‎3‎‎+‎|（‎-‎‎1‎‎2‎）﹣1|﹣2‎2‎tan30°﹣（π﹣2019）0‎ ‎=‎2‎‎6‎‎3‎+‎‎2﹣2‎2‎‎×‎3‎‎3‎-‎1‎ ‎=‎2‎‎6‎‎3‎+‎‎2‎-‎2‎‎6‎‎3‎-‎1‎ ‎＝1；‎ ‎（2）原式‎=a‎(a+b)(a-b)‎×b-ab-‎1‎a+b×‎b-ab ‎=-ab(a+b)‎-‎b-ab(a+b)‎‎ ‎ ‎=-‎bb(a+b)‎‎ ‎ ‎=-‎‎1‎a+b‎，‎ 当a‎=‎‎2‎，b＝2‎-‎‎2‎时，原式‎=-‎1‎‎2‎‎+2-‎‎2‎=-‎‎1‎‎2‎．‎ ‎20．（11分）胜利中学为丰富同学们的校园生活，举行“校园电视台主待人“选拔赛，现将36名参赛选手的成绩（单位：分）统计并绘制成频数分布直方图和扇形统计图，部分信息如下：‎ 请根据统计图的信息，解答下列问题：‎ ‎（1）补全频数分布直方图，并求扇形统计图中扇形D对应的圆心角度数；‎ ‎（2）成绩在D区域的选手，男生比女生多一人，从中随机抽取两人临时担任该校艺术节的主持人，求恰好选中一名男生和一名女生的概率．‎ ‎【解答】解：（1）80～90的频数为36×50%＝18，‎ 则80～85的频数为18﹣11＝7，‎ ‎95～100的频数为36﹣（4+18+9）＝5，‎ 补全图形如下：‎ 扇形统计图中扇形D对应的圆心角度数为360°‎×‎5‎‎36‎=‎50°；‎ ‎（2）画树状图为：‎ 共有20种等可能的结果数，其中抽取的学生恰好是一名男生和一名女生的结果数为12，‎ 所以抽取的学生恰好是一名男生和一名女生的概率为‎12‎‎20‎‎=‎‎3‎‎5‎．‎ ‎21．（11分）辰星旅游度假村有甲种风格客房15间，乙种风格客房20间．按现有定价：若全部入住，一天营业额为8500元；若甲、乙两种风格客房均有10间入住，一天营业额为5000元．‎ ‎（1）求甲、乙两种客房每间现有定价分别是多少元？‎ ‎（2）度假村以乙种风格客房为例，市场情况调研发现：若每个房间每天按现有定价，房间会全部住满；当每个房间每天的定价每增加20元时，就会有两个房间空闲．如果游客居住房间，度假村需对每个房间每天支出80元的各种费用．当每间房间定价为多少元时，乙种风格客房每天的利润m最大，最大利润是多少元？‎ ‎【解答】解：设甲、乙两种客房每间现有定价分别是x元、y元，‎ 根据题意，得：‎15x+20y=8500‎‎10x+10y=5000‎，‎ 解得x=300‎y=200‎，‎ 答：甲、乙两种客房每间现有定价分别是300元、200元；‎ ‎（2）设每天的定价增加了a个20元，则有2a个房间空闲，‎ 根据题意有：m＝（20﹣2a）（200+20a﹣80）＝﹣40a2+160a+2400＝﹣40（a﹣2）2+2560，‎ ‎∵﹣40＜0，‎ ‎∴当a＝2时，m 取得最大值，最大值为2560，此时房间的定价为200+2×20＝240元．‎ 答：当每间房间定价为240元时，乙种风格客房每天的利润w最大，最大利润是2560元．‎ ‎22．（11分）如图，一次函数y＝kx+b（k≠0）的图象与反比例函数y‎=‎m‎2‎‎-3mx（m≠0且m≠3）的图象在第一象限交于点A、B，且该一次函数的图象与y轴正半轴交于点C，过A、B分别作y轴的垂线，垂足分别为E、D．已知A（4，1），CE＝4CD．‎ ‎（1）求m的值和反比例函数的解析式；‎ ‎（2）若点M为一次函数图象上的动点，求OM长度的最小值．‎ ‎【解答】解：（1）将点A（4，1）代入y‎=‎m‎2‎‎-3mx，‎ 得，m2﹣3m＝4，‎ 解得，m1＝4，m2＝﹣1，‎ ‎∴m的值为4或﹣1；反比例函数解析式为：y‎=‎‎4‎x；‎ ‎（2）∵BD⊥y轴，AE⊥y轴，‎ ‎∴∠CDB＝∠CEA＝90°，‎ ‎∴△CDB∽△CEA，‎ ‎∴CDCE‎=‎BDAE，‎ ‎∵CE＝4CD，‎ ‎∴AE＝4BD，‎ ‎∵A（4，1），‎ ‎∴AE＝4，‎ ‎∴BD＝1，‎ ‎∴xB＝1，‎ ‎∴yB‎=‎4‎x=‎4，‎ ‎∴B（1，4），‎ 将A（4，1），B（1，4）代入y＝kx+b，‎ 得，‎4k+b=1‎k+b=4‎，‎ 解得，k＝﹣1，b＝5，‎ ‎∴yAB＝﹣x+5，‎ 设直线AB与x轴交点为F，‎ 当x＝0时，y＝5；当y＝0时x＝5，‎ ‎∴C（0，5），F（5，0），‎ 则OC＝OF＝5，‎ ‎∴△OCF为等腰直角三角形，‎ ‎∴CF‎=‎‎2‎OC＝5‎2‎，‎ 则当OM垂直CF于M时，由垂线段最知可知，OM有最小值，‎ 即OM‎=‎‎1‎‎2‎CF‎=‎‎5‎‎2‎‎2‎．‎ ‎23．（11分）如图，AB是⊙O的直径，点C为BD的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．‎ ‎（1）求证：△BFG≌△CDG；‎ ‎（2）若AD＝BE＝2，求BF的长．‎ ‎【解答】证明：（1）∵C是BC的中点，‎ ‎∴CD‎=‎BC，‎ ‎∵AB是⊙O的直径，且CF⊥AB，‎ ‎∴BC‎=‎BF，‎ ‎∴CD‎=‎BF，‎ ‎∴CD＝BF，‎ 在△BFG和△CDG中，‎ ‎∵‎∠F=∠CDG‎∠FGB=∠DGCBF=CD，‎ ‎∴△BFG≌△CDG（AAS）；‎ ‎（2）解法一：如图，连接OF，设⊙O的半径为r，‎ Rt△ADB中，BD2＝AB2﹣AD2，即BD2＝（2r）2﹣22，‎ Rt△OEF中，OF2＝OE2+EF2，即EF2＝r2﹣（r﹣2）2，‎ ‎∵CD‎=BC=‎BF，‎ ‎∴BD‎=‎CF，‎ ‎∴BD＝CF，‎ ‎∴BD2＝CF2＝（2EF）2＝4EF2，‎ 即（2r）2﹣22＝4[r2﹣（r﹣2）2]，‎ 解得：r＝1（舍）或3，‎ ‎∴BF2＝EF2+BE2＝32﹣（3﹣2）2+22＝12，‎ ‎∴BF＝2‎3‎；‎ 解法二：如图，过C作CH⊥AD于H，连接AC、BC，‎ ‎∵CD‎=‎BC，‎ ‎∴∠HAC＝∠BAC，‎ ‎∵CE⊥AB，‎ ‎∴CH＝CE，‎ ‎∵AC＝AC，‎ ‎∴Rt△AHC≌Rt△AEC（HL），‎ ‎∴AE＝AH，‎ ‎∵CH＝CE，CD＝CB，‎ ‎∴Rt△CDH≌Rt△CBE（HL），‎ ‎∴DH＝BE＝2，‎ ‎∴AE＝AH＝2+2＝4，‎ ‎∴AB＝4+2＝6，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ACB＝90°，‎ ‎∴∠ACB＝∠BEC＝90°，‎ ‎∵∠EBC＝∠ABC，‎ ‎∴△BEC∽△BCA，‎ ‎∴BCAB‎=‎BEBC，‎ ‎∴BC2＝AB•BE＝6×2＝12，‎ ‎∴BF＝BC＝2‎3‎．‎ 解法三：如图，连接OC，交BD于H，‎ ‎∵C是BD的中点，‎ ‎∴OC⊥BD，‎ ‎∴DH＝BH，‎ ‎∵OA＝OB，‎ ‎∴OH‎=‎‎1‎‎2‎AD＝1，‎ ‎∵OC＝OB，∠COE＝∠BOH，∠OHB＝∠OEC＝90°，‎ ‎∴△COE≌△BOH（AAS），‎ ‎∴OH＝OE＝1，‎ ‎∴CE＝EF‎=‎3‎‎2‎‎-‎‎1‎‎2‎=‎2‎2‎，‎ ‎∴BF‎=BE‎2‎+EF‎2‎=‎2‎‎2‎‎+(2‎‎2‎‎)‎‎2‎=‎2‎3‎．‎ ‎24．（12分）在平面直角坐标系中，将二次函数y＝ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x轴交于点A、B（点A在点B的左侧），OA＝1，经过点A的一次函数y＝kx+b（k≠0）的图象与y轴正半轴交于点C，且与抛物线的另一个交点为D，△ABD的面积为5．‎ ‎（1）求抛物线和一次函数的解析式；‎ ‎（2）抛物线上的动点E在一次函数的图象下方，求△ACE面积的最大值，并求出此时点E的坐标；‎ ‎（3）若点P为x轴上任意一点，在（2）的结论下，求PE‎+‎‎3‎‎5‎PA的最小值．‎ ‎【解答】解：（1）将二次函数y＝ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到的抛物线解析式为y＝a（x﹣1）2﹣2，‎ ‎∵OA＝1，‎ ‎∴点A的坐标为（﹣1，0），代入抛物线的解析式得，4a﹣2＝0，‎ ‎∴a=‎‎1‎‎2‎，‎ ‎∴抛物线的解析式为y‎=‎1‎‎2‎(x-1‎)‎‎2‎-2‎，即y‎=‎1‎‎2‎x‎2‎-x-‎‎3‎‎2‎．‎ 令y＝0，解得x1＝﹣1，x2＝3，‎ ‎∴B（3，0），‎ ‎∴AB＝OA+OB＝4，‎ ‎∵△ABD的面积为5，‎ ‎∴S‎△ABD‎=‎1‎‎2‎AB⋅yD=‎5，‎ ‎∴yD‎=‎‎5‎‎2‎，代入抛物线解析式得，‎5‎‎2‎‎=‎1‎‎2‎x‎2‎-x-‎‎3‎‎2‎，‎ 解得x1＝﹣2，x2＝4，‎ ‎∴D（4，‎5‎‎2‎），‎ 设直线AD的解析式为y＝kx+b，‎ ‎∴‎4k+b=‎‎5‎‎2‎‎-k+b=0‎，解得：k=‎‎1‎‎2‎b=‎‎1‎‎2‎，‎ ‎∴直线AD的解析式为y‎=‎1‎‎2‎x+‎‎1‎‎2‎．‎ ‎（2）过点E作EM∥y轴交AD于M，如图，设E（a，‎1‎‎2‎a‎2‎‎-a-‎‎3‎‎2‎），则M（a，‎1‎‎2‎a+‎‎1‎‎2‎），‎ ‎∴EM=‎1‎‎2‎a+‎1‎‎2‎-‎1‎‎2‎a‎2‎+a+‎3‎‎2‎=-‎1‎‎2‎a‎2‎+‎3‎‎2‎a+2‎，‎ ‎∴S△ACE＝S△AME﹣S△CME‎=‎1‎‎2‎×EM⋅1=‎1‎‎2‎(-‎1‎‎2‎a‎2‎+‎3‎‎2‎a+2)×1=-‎1‎‎4‎(a‎2‎-3a-4)‎，‎ ‎=-‎1‎‎4‎(a-‎3‎‎2‎‎)‎‎2‎+‎‎25‎‎16‎‎，‎ ‎∴当a‎=‎‎3‎‎2‎时，△ACE的面积有最大值，最大值是‎25‎‎16‎，此时E点坐标为（‎3‎‎2‎‎，-‎‎15‎‎8‎）．‎ ‎（3）作E关于x轴的对称点F，连接EF交x轴于点G，过点F作FH⊥AE于点H，交轴于点P，‎ ‎∵E（‎3‎‎2‎‎，-‎‎15‎‎8‎），OA＝1，‎ ‎∴AG＝1‎+‎3‎‎2‎=‎‎5‎‎2‎，EG‎=‎‎15‎‎8‎，‎ ‎∴AGEG‎=‎5‎‎2‎‎15‎‎8‎=‎‎4‎‎3‎，‎ ‎∵∠AGE＝∠AHP＝90°‎ ‎∴sin‎∠EAG=PHAP=EGAE=‎‎3‎‎5‎，‎ ‎∴PH=‎3‎‎5‎AP，‎ ‎∵E、F关于x轴对称，‎ ‎∴PE＝PF，‎ ‎∴PE‎+‎‎3‎‎5‎AP＝FP+HP＝FH，此时FH最小，‎ ‎∵EF‎=‎15‎‎8‎×2=‎‎15‎‎4‎，∠AEG＝∠HEF，‎ ‎∴sin∠AEG=sin∠HEF=AGAE=FHEF=‎‎4‎‎5‎，‎ ‎∴FH=‎4‎‎5‎×‎15‎‎4‎=3‎．‎ ‎∴PE‎+‎‎3‎‎5‎PA的最小值是3．‎ ‎25．（14分）如图，在以点O为中心的正方形ABCD中，AD＝4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．‎ ‎（1）求证：△DEF是等腰直角三角形；‎ ‎（2）当点H恰好落在线段BC上时，求EH的长；‎ ‎（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．‎ ‎【解答】（1）证明：∵四边形ABCD是正方形，‎ ‎∴∠DAC＝∠CAB＝45°，‎ ‎∴∠FDE＝∠CAB，∠DFE＝∠DAC，‎ ‎∴∠FDE＝∠DFE＝45°，‎ ‎∴∠DEF＝90°，‎ ‎∴△DEF是等腰直角三角形；‎ ‎（2）设OE＝t，连接OD，‎ ‎∴∠DOE＝∠DAF＝90°，‎ ‎∵∠OED＝∠DFA，‎ ‎∴△DOE∽△DAF，‎ ‎∴OEAF‎=ODAD=‎‎2‎‎2‎，‎ ‎∴AF=‎‎2‎t，‎ 又∵∠AEF＝∠ADG，∠EAF＝∠DAG，‎ ‎∴△AEF∽△ADG，‎ ‎∴AEAD‎=‎AFAG，‎ ‎∴AG⋅AE=AD⋅AF=4‎2‎t，‎ 又∵AE＝OA+OE＝2‎2‎‎+‎t，‎ ‎∴AG=‎‎4‎2‎t‎2‎2‎+t，‎ ‎∴EG＝AE﹣AG‎=‎t‎2‎‎+8‎‎2‎2‎+t，‎ 当点H恰好落在线段BC上∠DFH＝∠DFE+∠HFE＝45°+45°＝90°，‎ ‎∴△ADF∽△BFH，‎ ‎∴FHFD‎=FBAD=‎‎4-‎2‎t‎4‎，‎ ‎∵AF∥CD，‎ ‎∴FGDG‎=AFCD=‎‎2‎t‎4‎，‎ ‎∴FGDF‎=‎‎2‎t‎4+‎2‎t，‎ ‎∴‎4-‎2‎t‎4‎‎=‎‎2‎t‎4+‎2‎t，‎ 解得：t1‎=‎10‎-‎‎2‎，t2‎=‎10‎+‎‎2‎（舍去），‎ ‎∴EG＝EH‎=t‎2‎‎+8‎‎2‎2‎+t=‎(‎10‎-‎2‎‎)‎‎2‎+8‎‎2‎2‎+‎10‎-‎‎2‎=3‎10‎-5‎‎2‎；‎ ‎（3）过点F作FK⊥AC于点K，‎ 由（2）得EG‎=‎t‎2‎‎+8‎‎2‎2‎+t，‎ ‎∵DE＝EF，∠DEF＝90°，‎ ‎∴∠DEO＝∠EFK，‎ ‎∴△DOE≌△EKF（AAS），‎ ‎∴FK＝OE＝t，‎ ‎∴S‎△EFG‎=‎1‎‎2‎EG⋅FK=‎t‎3‎‎+8t‎4‎2‎+2t．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 9:56:15；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎