2020-2021学年新初三数学上册知识点讲解 点和圆、直线和圆的位置关系 44页

2020-2021 学年新初三数学上册知识点讲解 点和圆、直线和圆的位置关系 专题 06 点和圆、直线和圆的位置关系专题详解 .........................................................................................................1 24.2 点和圆、直线和圆的位置关系 ..............................................................................................................................2 知识框架 .............................................................................................................................................................................2 一、基础知识点 ...............................................................................................................................................................3 知识点 1 圆的确定 .............................................................................................................................................................. 3 知识点 2 点和圆的位置关系 ........................................................................................................................................... 3 知识点 3 三角形的外接圆 ................................................................................................................................................ 4 知识点 4 反证法................................................................................................................................................................... 4 知识点 5 直线与圆的位置关系 ....................................................................................................................................... 5 知识点 6 切线的判定与性质 ........................................................................................................................................... 6 知识点 7 切线长定理 ......................................................................................................................................................... 7 知识点 8 三角形内切圆 ..................................................................................................................................................... 8 二、方法与思路 ............................................................................................................................................................ 11 方法 1 切线的证明技巧 ................................................................................................................................................... 11 方法 2 利用切线的性质求角度 ..................................................................................................................................... 19 方法 3 利用切线的性质求线段长 ................................................................................................................................ 23 方法 4 利用切线的性质证明 ......................................................................................................................................... 28 方法 5 切线与勾股定理（方程思想） ....................................................................................................................... 30 方法 6 切割线图构矩形 ................................................................................................................................................... 33 方法 7 双切线图................................................................................................................................................................. 36 三、典型题型 ................................................................................................................................................................. 39 题型 1 点与圆的位置关系（d 与 r） .......................................................................................................................... 39 题型 2 直线与圆的位置关系（d 与 r） ..................................................................................................................... 40 题型 3 切线的性质与判定 .............................................................................................................................................. 40 题型 4 切线长定理 ............................................................................................................................................................ 41 题型 5 三角形的内心和外心 ......................................................................................................................................... 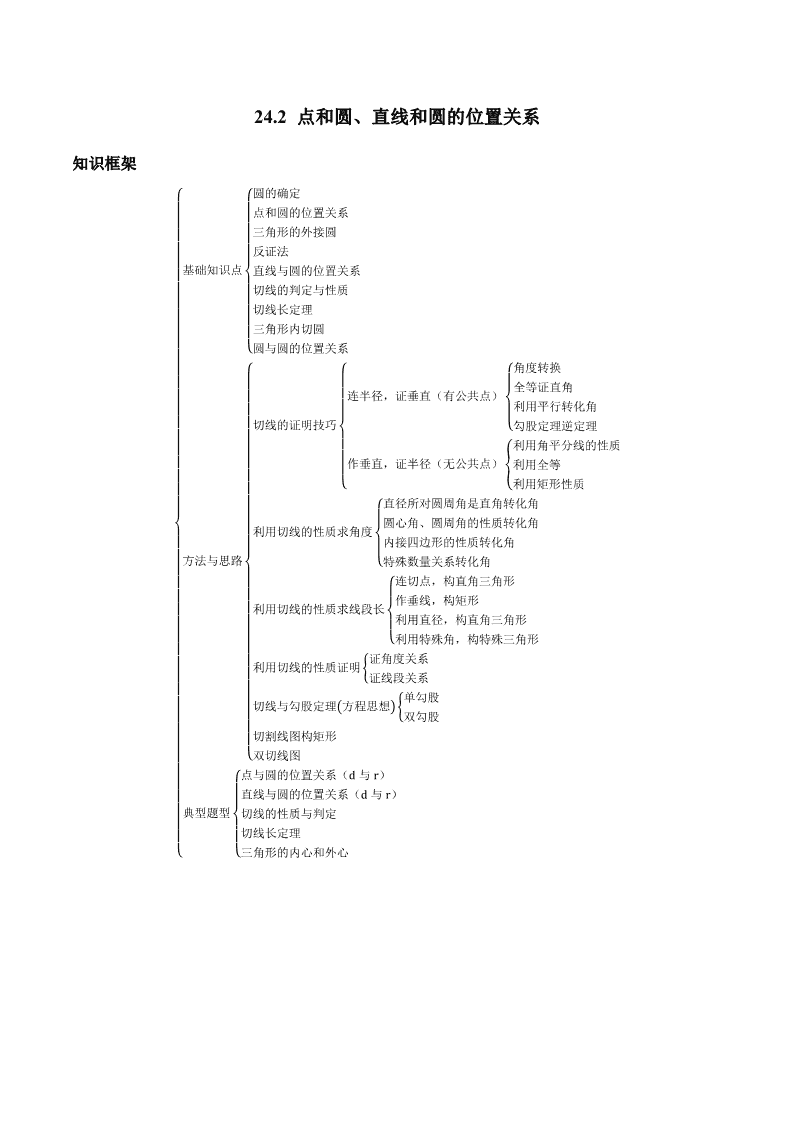42 24.2 点和圆、直线和圆的位置关系 知识框架 { 基础知识点 { 圆的确定 点和圆的位置关系 三角形的外接圆 反证法 直线与圆的位置关系 切线的判定与性质 切线长定理 三角形内切圆 圆与圆的位置关系 方法与思路 { 切线的证明技巧 { 连半径，证垂直（有公共点） { 角度转换 全等证直角 利用平行转化角 勾股定理逆定理 作垂直，证半径（无公共点） { 利用角平分线的性质 利用全等 利用矩形性质 利用切线的性质求角度 { 直径所对圆周角是直角转化角 圆心角、圆周角的性质转化角 内接四边形的性质转化角 特殊数量关系转化角 利用切线的性质求线段长 { 连切点，构直角三角形 作垂线，构矩形 利用直径，构直角三角形 利用特殊角，构特殊三角形 利用切线的性质证明 { 证角度关系 证线段关系 切线与勾股定理(方程思想) { 单勾股 双勾股 切割线图构矩形 双切线图 典型题型 { 点与圆的位置关系（d 与 r） 直线与圆的位置关系（d 与 r） 切线的性质与判定 切线长定理 三角形的内心和外心 一、基础知识点 知识点 1 圆的确定 1）经过一个已知点 A 可画无数个圆。 2）经过已知两点 A，B 作圆，可画无数个，它们的圆心在线段 AB 的垂直平分线上 3）经过同一直线上三个点 A、B、C 的圆是不存在的。 4）经过不再同一直线上的三个点 A、B、C 可画一个圆，而且只能作一个圆。 例 1.过一点可以作 个圆，过两点可以作 个圆，过三点可以作 个圆。 【答案】：无数；无数；1 个或 0 个 【解析】：经过 1 点，可以画无数个圆； 经过 2 点，可以画无数个圆，圆心在两点连线的垂直平分线上； 经过不在同一直线上的 3 点可以画 1 个圆；经过在同一直线上的 3 点，圆不存在 例 2.已知 A、B、C 是平面内三点，AB=3，BC=3，AC=6，下列说法正确的是（ ） A.可以画一个圆，使 A、B、C 都在圆上 B.可以画一个圆，使 A、B 在圆上，C 在圆外 C.可以画一个圆，使 A、C 在圆上，B 在圆外 D.可以画一个圆，使 B、C 在圆上，A 在圆内 BC 【答案】：B 【解析】：∵AB=3，BC=3，AC=6 ∴A、B、C 三点在同一条直线上，具体位置关系如下图所示： A.错误，三点在同一条直线上，不可能画圆； B.正确，使 A、B 在圆上，则圆心在 AB 的垂直平分线上，点 C 在圆外； C.错误，使 A、C 在圆上，则圆心在 AC 的垂直平分线上，点 B 在圆内； D.错误，使 B、C 在圆上，则圆心在 BC 的垂直平分线上，点 A 在圆外。 知识点 2 点和圆的位置关系 1）点和圆的位置关系有 3 种：圆外、圆上、圆内 2）设O 的半径为 r，点 P 到圆心的距离 OP=d，则： P 在圆外⟺d>r P 在圆上⟺d=r P 在圆内⟺d0，则 ax>bx 用反证法，假设 a>0，则 axr⟺无交点 例 1.已知，圆的直径为 13cm，直线到圆心的距离为 d，当 d=8cm 时，直线与圆 ，当 d=6.5cm 时， 直线与圆 ，当 d 小于 6.5cm 时，直线与圆 。 【答案】：相离；相切；相交 【解析】：∵圆的直径为 13cm ∴圆的半径 r=6.5cm 当距离 d＞r 时，相离；当 d=r 时，相切；当 d＜r 时，相交 例 2.已知O 的直径为 10cm，如果圆心 O 到直线푙的距离为 4cm，求直线푙与O 有几个交点？ 【答案】：2 个 【解析】：∵O 的直径为 10cm ∴O 的半径 r=5cm ∵d=4cm，d＜r ∴直线与O 相交 ∴有 2 个交点 知识点 6 切线的判定与性质 1）切线的性质：圆的切线垂直于过切点的半径 2）证圆的切线有两种方法： ①连半径，证垂直，即已知半径，证明直线与这条半径垂直 ②作垂线，证半径，即作出圆心到直线的垂线，证明垂线段长等于半径 注：已知圆的切线时，作过切点的半径是常用的辅助线，因为圆的切线垂直于过切点的半径。 例 1.如图，AB 是O 的直径，BC 是O 的弦，D 为 BA 延长线上一点，∠B=25°，当∠D 等于多少度时， CD 与O 相切。 【答案】：40° 【解析】：如下图，连接 CO ∵CD 与O 相切 ∴CD⊥CO，∠DCO=90° ∵∠B=25°，OB=OC=r ∴∠OCB=∠B=25° ∴∠D=180°－90°－25°－25°=40° 例 2.已知 AB 是O 的直径，BC 是O 的切线，切点为 B，OC 平行于弦 AD，求证：DC 是O 的切线。 【答案】：见解析 【解析】：如图，连接 OD ∵CB 是O 的切线 ∴∠CBO=90° ∵AD∥CO ∴∠DAO=∠COB，∠ADO=∠DOC ∵AO=OD=r ∴∠OAD=∠ODA ∴∠DAO=∠COB=∠ADO=∠DOC ∵CO=CO，OD=OB=r ∴△COD≌△COB ∴∠CDO=∠CBO=90° ∴DC 是O 的切线 知识点 7 切线长定理 1）经过圆外一点作圆的切线，这点和切点之间的线段叫作这点到圆的切线长。 2）从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。 如上图，若 PA、PB 是O 的切线，点 A、B 为切点，则： ①PA=PB；②∠APO=∠BPO；③PO 是 AB 的垂直平分线 例 1.如图，PA，PB 分别切O 于 A、B 两点，直线 OP 交O 于 D、E 两点，交 AB 于点 C。若∠APB=50°， 求∠OAC 的度数。 【答案】：25° 【解析】：∵PA、PB 是O 的切线，∠APB=50° ∴∠APO=∠BPO=25°，∠OAP=90°，∠OCA=90° ∴∠AOC=65° ∴∠OAC=25° 例 2.如图，PA 和 PB 是O 的切线，点 A 和点 B 是切点，AC 是O 的直径，已知∠P=40°，求∠ACB 的大 小。 【答案】：70° 【解析】：如图，连接 OP，OB ∵PA、PB 是O 的切线，∠APB=40° ∴∠APO=∠BPO=20°，∠OAP=∠OBP=90° ∴∠AOP=∠BOP=70° ∴∠COB=40° ∵OC=OB=r ∴∠OCB=∠OBC ∴∠OCB=70° 知识点 8 三角形内切圆 1）与三角形各边都相切的圆叫作三角形的内切圆。内切圆的圆心是三角形三条角平分线的交点，叫作 三角形的内心。 2）内心特点：内心到三角形三边的距离相等 3）三角形四心： ①外心：三角形外接圆的圆心，三边垂直平分线的交点。 ②内心：三角形内切圆的圆心，三内角角平分线的交点。 ③重心：三条中线的交点。 ④垂心：三条高的交点。 例 1.如图，O 为 Rt△ABC 的内切圆，切点为 D，E，F，半径为 r，∠C=90°，AB，BC，AC 的长分别 为 c，a，b，求 r。 【答案】：푎+푏−푐 2 【解析】：如图，连接 OD，OF ∵点 D、F 是内切圆与△ABC 的切点 ∴OD⊥CB，OF⊥AC，AE=AF，CF=CD，BD=BE ∴四边形 OFCD 为正方形 ∴CF=CD=r ∴AE=AF=b－r，BE=BD=a－r ∵AE+BE =AB =c ∴b－r+a－r=c ∴r=푎+푏−푐 2 例 2.如图，在△ABC 中，∠C=90°，AC=3，BC=4，I 为△ABC 的内心，IE⊥AB 于 E，求 IE，AE，BI 的长度。 【答案】：IE=1，AE=2，BI=√10 【解析】：如图，连接 AI，CI，过点 I 作 BC 的垂线，交 BC 于点 N，过点 I 作 AC 的垂线，交 AC 于点 M ∵点 I 是△ABC 的内心 ∴点 I 到△ABC 的三边距离相等，即 IE=IN=IM，设 IE=h ∵∠C=90°，AC=3，BC=4 ∴AB=5，푆△퐴퐵퐶 = 1 2 ∙ 3 ∙ 4 = 6 又∵푆△퐴퐵퐶 = 푆△퐴퐵퐼 + 푆△퐴퐶퐼 + 푆△퐵퐶퐼 ∴6=1 2 ∙ 5 ∙ h + 1 2 ∙ 3 ∙ h + 1 2 ∙ 4 ∙ h，解得：h=1 ∵IM=IN，∠ACB=∠IMC=∠INC=90° ∴四边形 IMCN 为正方形 ∴MC=NC=IM=1 ∴AE=AM=2，NB=3 在 Rt△INB 中，根据勾股定理，IB=√10 二、方法与思路 方法 1 切线的证明技巧 一、连半径，证垂直（有公共点） 解题技巧：已知直线与圆的公共点，连接关于该点的半径，只需证这个半径垂直于直线即可证明为切线。 （1）角度转换 解题技巧：利用圆和几何中的性质，进行角度转化，最终证明出半径与直线的夹角为直角。 例 1.如图，已知O 是△ABC 的外接圆，且 AB=BC=CD，AB∥CD，连接 BD。证：BD 是O 的切线。 【答案】：见解析 【解析】：如图，连接 OB ∵AB=BC=CD ∴∠A=∠ACB，∠CBD=∠D ∵AB∥CD ∴∠ABC=∠BCD ∵∠A+∠ACB+∠ABC=180°，∠CBD+∠D+∠BCD=190° ∴∠A+∠ACB=∠CBD+∠D ∴∠A=∠ACB=∠CBD=∠D 以下步骤证明 BO 平分∠ABC（根据 24.1 中的方法 6，是可以直接得出等腰三角形 BAC 中，BO 是三线合一 的，即 BO 是∠ABC 的平分线），此题我们用全等再次证明，连接 OA，OC ∵OA=OC=r，OB=OB，AB=BC ∴△AOB≌△COB，∴∠ABO=∠CBO 证明结束，继续本体证明 ∵∠A+∠ACB+∠ABC=180°，∴∠A+∠OBC=90°，∴∠CBD+∠OBC=90°，即∠OBD=90° ∴BD 是O 的切线 例 2.如图，已知 BC 是⊙ O的直径，AC 切⊙ O于点 C，AB 交⊙ O于点 D，点 E 为 AC 中点，连接 DE。 求证：ED 是⊙ O的切线。 【答案】：见解析 【解析】：如图，连接 OD、CD ∵BC 是O 的直径 ∴∠BDC=90°，∴∠ADC=90°，∴△ADC 是直角三角形 ∵点 E 是 AC 的中点 ∴DE=AE=EC，∴∠EDC=∠ECD ∵DO=OC=r，∴∠ODC=∠DCO ∵AC 是O 的切线 ∴∠OCA=90°，即∠DCO+∠DCE=90° ∴∠ODC+∠EDC=90°，即∠EDO=90° ∴DE 是O 的切线 （2）全等证直角 解题技巧：证全等得出角度关系，证明直角 例3.如图，在Rt△ABC 中，∠BAC＝90°，BD是角平分线，以点D为圆心，DA为半径的⊙D与AC相交于 点E。求证：BC是⊙D的切线； 【答案】：见解析 【解析】：如图，过点D作DH⊥BC交BC于点H ∵BD是∠ABC的角平分线 ∴∠ABD=∠HBD 在△ABD与△HBD中 { ∠퐵퐴퐷 = ∠퐵퐻퐷 = 90° ∠퐴퐵퐷 = ∠퐻퐵퐷 퐵퐷 = 퐵퐷 ∴△ABD≌△HBD ∴DH=AD=r ∴BC为⊙D的切线 例4.如图，PA是⊙O的切线，A是切点，AC是直径，AB是弦，连接PB、PC，PC交AB于点E，且PA＝PB。 求证：PB是⊙O的切线 【答案】：见解析 【解析】：如下图，连接OB，OP ∴OB=OA=r 在△AOP与△BOP中 { 퐴푂 = 퐵푂 푂푃 = 푂푃 퐴푃 = 퐵푃 ∴△AOP≌△BOP ∵A是切点 ∴∠OAP=90°=∠OBP ∴PB是⊙O的切线 （3）利用平行转化角 解题技巧：利用平行中的角度关系，转化角度，进而推导出直角。 例5.如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆。求证：AD是⊙O 的切线 【答案】：见解析 【解析】：如下图，连接AO并延长，交CB于点M ∵⊙O为△ABC的外接圆 ∴点O是三角形的内心，即垂直平分线的交点 ∴AE是CB的垂直平分线，AM⊥CB ∵AD∥CB ∴AM⊥AD ∴AD是⊙O的切线 例 6.如图，已知在△ABC 中，AB=AC，以 AB 为直径作⊙O。交 BC 于点 D，交 AC 于点 E，过点 D 作 DF⊥AC 于点 F。证明：DF 是⊙ O的切线。 【答案】：见解析 【解析】：如题，连接 OD ∵OB=OD，AB=AC ∴∠ODB=∠B=∠C ∴OD∥AC ∵DF⊥AC，即∠AFD=90° ∴∠ODF=90° ∴DF 是O 的切线 （4）勾股定理的逆定理 解题技巧：已知三角形三边关系，利用勾股定理的逆定理，可以推导出直角。 例 7.如图，AB 是O 的直径，点 P 为 AB 延长线上一点，点 C 为O 上一点，PC=8，PB=4，AB=12。求 证：PC 是O 的切线。 【答案】：见解析 【解析】：如图，连接 OC ∵AB=12，∴r=6，∴AO=OB=OC=6 ∵PB=4，∴PO=10 在三角形 OCP 中，OC=6，CP=8，OP=10 满足勾股定理的逆定理 ∴∠OCP=90° ∴CP 是O 的切线 例 8.如图，点 P 是O 的直径 AB 的延长线上的一点，点 Q 是O 上一点，且满足푃푄2 = 푃퐴 ∙ 푃퐵，求证： PQ 与O 相切。 【答案】：见解析 【解析】：如图，连接 QO 푃푄2 = 푃퐴 ∙ 푃퐵 =（PO+AO）∙ （푃푂 − 푂퐵） =（PO+OQ）∙ （푃푂 − 푂푄） =푃푂2 − 푂푄2 ∴PQ、PO、OQ 三边长满足勾股定理的逆定理 ∴∠OQP=90° ∴QP 是O 的切线 二、作垂线，证半径（无公共点） 解题技巧：不知直线与圆的交点，过圆心作直线的垂线，证明垂线段长度 d 等于半径 r 即可。 （1）利用角平分线的性质 解题技巧：角平分线上的点到两边的距离相等，利用这个性质，易于证明 d=r。 例 1.如图，△ABC 中，AB=AC，D 为 BC 的中点，以 D 为圆心的圆与 AB 相切于点 E，求证：AC 与O 相切 【答案】：见解析 【解析】：如图，连接 DE，过点 D 作 AC 的垂线角 AC 于点 F ∵AB=AC，D 是 BC 的中点 ∴AD 是∠BAC 的角平分线 ∵AB 是O 的切线 ∴DE⊥AB ∵DF⊥AC ∴DF=DE ∴AC 是O 的切线 （2）利用全等 解题技巧：通过全等得出边之间的长度关系，推导出垂线段 d=r 证切线。 例 2.如图，同心圆 O，大圆的弦 AB=CD，且 AB 是小圆的切线，切点为 E，求证：CD 是小圆的切线。 【答案】：见解析 【解析】：如图，连接 OE，OA，OC，过点 O 作 CD 垂线交 CD 于点 F 设大圆半径为 R，小圆半径为 r ∵AB 是小圆的切线，∴∠OEA=90°，OE=r 根据垂径定理，AE=1 2 퐴퐵，CF=1 2 퐶퐷 ∵AB=CD，∴AE=CF ∵AO=CO=R，∠OEA=∠OFC=90° ∴△OEA≌△OFA ∴OF=OE=r ∴CD 是小圆的切线 例 3.如图，四边形 ABCD 中，∠A=∠ABC=90°，AD+BC=CD，求证：以 AB 为直径的圆与 CD 相切。 【答案】：见解析 【解析】：如图，取 AB 的中点 O，则 AO=OB=r，连接 OD 并延长角 BC 反向延长线与点 E，过点 O 作 DC 的垂线交于点 F。 ∵∠A=∠ABC=90°，∴∠A=∠ABE=90° ∵∠AOD=∠EOB，AO=OB=r ∴△AOD≌△BOE ∴EB=AD，∠E=∠ADO ∵AD+BC=DC ∴EC=DC ∴∠ODF=∠E=∠ADO ∵∠A=∠OFD=90°，OD=OD ∴△ADO≌△FDO ∴OF=OA=r ∴以 AB 为直径的圆与 CD 相切 （3）利用矩形性质 解题技巧：作垂线构造出矩形或证明四边形是矩形，利用矩形对边相等的性质推导出 d=r。 例 4.如图，点 O 为正方形 ABCD 的对角线 AC 上一点，以 O 为圆心，OA 为半径的O 与 BC 相切于 M 点，求证：CD 是O 的切线。 【答案】：见解析 【解析】：如图，连接 OM，过点 O 作 DC 的垂线，交 DC 于点 N ∵BC 是O 的切线，∴∠OMC=90°，OM=r ∵四边形 ABCD 是矩形，∴∠MCN=90° ∵ON⊥DC，∴∠ONC=90° ∴四边形 OMCN 是矩形 ∵四边形 ABCD 是正方形 ∴∠MCO=45°，∴∠MOC=45°，∴OM=MC ∴矩形 OMCN 是正方形 ∴ON=OM=r ∴CD 是O 的切线 例5.如图，在四边形ABCD中，AD∥BC，AB⊥BC，⊙O分别与边AB，AD，DC相切，切点分别为E，G， F，其中E为边AB的中点。求证：BC与⊙O相切。 【答案】：见解析 【解析】：连接OG，OE.作OH⊥BC交BC于H. ∵AB⊥BC，AD∥BC ∴∠A＝∠B＝90° ⊙O与AB相切于点E，O与AD相切于点G ∴∠OEA＝∠OGA＝90°，OE＝OG＝r ∴四边形OEAG是正方形 ∴AE＝OG＝r ∵E为AB的中点 ∴AE＝EB ∴EB＝OG＝r ∵∠B＝∠OEB＝∠OHB＝90°，OE＝EB＝r ∴四边形OEBH为正方形， ∴OH＝EB＝r 即BC与⊙O相切 方法 2 利用切线的性质求角度 解题技巧：已知切线，连接过切点的半径，构造出直角，再利用圆有关的性质转化角度求进而角。 一、直径所对圆周角是直角转化角 例 1.如图，△ABC 是O 的内接三角形，过点 A 的切线交 BC 的延长线与点 P，若∠B=34°，求∠CAP 的大小。 【答案】：34° 【解析】：如图，连接 AO 并延长，交O 于点 D，连接 DC ∵AP 是O 的切线 ∴∠OAP=90° ∵AD 是直径，∴∠ACD=90° ∵∠B=34°，∴∠D=34° ∴∠DAC=56° ∴∠CAP=34° 例 2.如图，AB 是O 的直径，点 C 是O 外的一点，CB 与O 相切于点 B，AC 交O 于点 D，点 E 是 优弧퐵퐴퐷̂上的一点（不与 A，B，D 重合），若∠C=48°，求∠AED 的大小。 【答案】：48°或 132° 【解析】：如图，连接 DB，点 E 存在如图所示两种情况 ∵CB 是O 的切线，∴∠ABC=90° ∵AB 是O 的直径，∴∠ADB=∠CDB=90° ∵∠C=48°，∴∠CBD=52° ∴∠DBA=48° ∵四边形 A퐸1퐷퐵是内接四边形 ∴∠A퐸1D=180°－∠ABD=132° ∵四边形 A퐸1D퐸2是内接四边形 ∴∠A퐸2퐷=180°－∠A퐸1D=48° 二、圆心角、圆周角的性质转化角 例 1.如图，BE 是O 的直径，点 A 和点 D 是O 上的两点，过点 A 作O 的切线交 BE 的延长线于点 C，若∠ADE=25°，求∠C。 【答案】：40° 【解析】：如图，连接 AO ∵AC 是O 的切线 ∴∠OAC=90° ∵∠ADE=25°，∴∠AOE=50° ∴∠ACO=40° 例 2.如图，PA，PB 切O 于 A，B 两点，C 为优弧퐴퐶퐵̂上一点，已知∠BCA=50°，求∠APB 的大小。 【答案】：80° 【解析】：连接 OB、OA ∵PB、PA 是O 的切线 ∴∠OBP=∠OAP=90° ∵∠BCA=50° ∴∠POA=100° 在四边形 BPAO 中，∠BPA=360°－100°－90°－90°=80° 三、内接四边形的性质转化角 例 1.如图，AB 是O 的直径，点 C 在O 上，过点 C 的切线与 BA 的延长线交于点 D，且∠D=40°，点 E 是퐴퐶퐵̂上的一点（不与点 A，C，B 重合），求∠BEC 的大小。 【答案】：115°或 65° 【解析】：连接 AC，OC，如下图，点 E 存在 2 处 ∵DC 是O 的切线，∴∠OCD=90° ∵∠D=40°，∴∠COD=50° ∴∠COB=130°，∴∠CAB=65° ∵四边形 CAB퐸1是内接四边形，∴∠C퐸1퐵=180°－∠CAB=115° ∵四边形 C퐸2퐵퐸1是内接四边形，∴∠C퐸2퐵=180°－∠C퐸1퐵=65° 例 2.如图，点 C 是O 的直径 BA 的延长线上一点，CD 切O 于点 D，若∠DEB=110°，求∠C 的大小。 【答案】：50° 【解析】：如图，连接 AD、OD ∵CD 是O 的切线，∴∠CDO=90° ∵四边形 ADEB 是内接四边形，∠E=110° ∴∠DAO=70° ∵OA=OD=r ∴∠ADO=∠DAO=70° ∴∠CDA=20° ∴∠DCA=∠DAO－∠CDA=70°－20°=50° 四、特殊数量关系转化角 例 1.如图，四边形 ABCD 是平行四边形，点 O 为 BC 的延长线上的一点，经过 A，C，D 三点的O 恰好 与 AB 相切，求∠OCD 的大小。 【答案】：30° 【解析】：如图，连接 AO，∠CD 于点 E ∵AB 是O 的切线，∴∠BAO=90° ∵四边形 ABCD 是平行四边形，∴AB∥CD，AD∥BC，∴∠AEC=∠CEO=90°，∠DCO=∠ADC 设∠DCO=x，则∠ADC=x ∴∠AOC=2x 在△CEO 中，∠ECO+∠COE+∠CEO=180°，即 x+2x+90°=180° 解得：x=30° ∴∠DCO=30° 例 2.如图，菱形 ABOC 的边 AB 与O 相切于点 D，若点 D 是 AB 的中点，求∠A 的大小。 【答案】：120° 【解析】：连接 AO，OD ∵AB 是O 的切线，∴OD⊥AB ∵点 D 是 AB 的中点，∴AD 是△OAB 的中线 ∴OB=AO ∵四边形 ABOC 是菱形 ∴AB=OB ∴△ABO 是正三角形，∴∠OAB=60° ∴∠BAC=120° 方法 3 利用切线的性质求线段长 一、连切点，构直角三角形 解题技巧：过圆心连接切点，构造直角三角形，运用勾股定理计算求线段长。 例 1.如图，BC 是O 的直径，AD 是O 的切线，切点为 D，AD 与 CB 的延长线交于点 A，∠C=30°， AB=2，求 AD 的长。 【答案】：2√3 【解析】：连接 DO ∵AD 是O 的切线，∴∠ADO=90° ∵∠C=30°，OD=OC=r ∴∠ODC=∠C=30° ∴在△ADC 中，∠A=180°－∠ADC－∠C=180°－90°－30°－30°=30° ∴△AOD 是含有 30°的直角三角形 设半径为 r，则 DO=r，OB=r，OA=2r 又∵OA=AB+OB=2+r=2r 解得：r=2 ∴OD=2，AO=4，AD=2√3 例 2.如图，在△ABC 中，AB=6，BC=3，AC=3√3，以 C 为圆心的圆与 AB 相切于点 D，求C 的半径。 【答案】：3 2 √3 【解析】：连接 AD ∵AB 是O 的切线，∴∠CDA=∠CDB=90° ∵AB=6，BC=3，AC=3√3，三边满足勾股定理的逆定理 ∴∠ACB=90°，且∠A=30°，∠B=60° ∴在 Rt△BCD 中，∠CDB=90°，∠B=60°，∠DCB=30°，BC=3 ∴DB=3 2 ，DC=3 2 √3 = 푟 二、作垂线，构矩形 解题技巧：圆心连切点，可构造出一个直角，继续作垂线，又可构造出一个直角，从而构造出矩形。再利 用矩形对边相等等性质求解计算。 例 1.如图，AB 是O 的直径，ED 与O 相切于点 C，AD 交O 于点 F，若 AC 平分∠BAD，且 CD=4， AF=2，求O 的半径。 【答案】：√17 【解析】：连接 OC，OD，过点 O 作 AD 的垂线交 AD 于点 H ∵CE 是O 的切线，∴∠OCD=90° ∵AC 是∠BAD 的角平分线，∴∠OAC=∠DAC ∵OA=OC，∴∠OAC=∠OCA ∴∠OCA=∠CAD，∴OC∥AD ∴∠D=90° ∵OH⊥AD，∴四边形 OHDC 是矩形 ∴OH=CD=4 ∵OA=OF=r，∴△OAF 是等腰三角形 ∵AF=2，∴AG=HF=1 ∴在 Rt△OAG 中，根据勾股定理 OA=√17 例 2.如图，AB 为O 的直径，CE 与O 相切于 E，AC⊥CE 宇 C，AC 交O 于 M，若 AM=2CM=2，求 CE 的长。 【答案】：√3 【解析】：连接 OE，OM，过点 O 作 AC 的垂线交 AC 于点 N ∵CE 是O 的切线，∴∠OEC=90° ∵AC⊥CE，ON⊥AC ∴四边形 OECN 是矩形 ∵OA=OM，ON⊥AM，AM=2 ∴AN=NM=1 ∵MC=1，∴NC=2=OE=r=OM 在 Rt△MON 中，MO=2，MN=1，∴NO=√3 = 퐶퐸 三、利用直径，构直角三角形 解题技巧：连直径所对圆周角，构造直角三角形，利用直角三角形勾股定理求边。 例 1.如图，在 Rt△ABC 中，∠ACB=90°，AC=6，BC=8，点 D 是 AB 的中点，以 CD 为直径作O 分别 与 AC，BC 交于点 E，F，过点 F 的切线 FG 交 AB 于点 G，求 FG 的长。 【答案】：12 5 【解析】：如图，连接 OD，DF ∵∠ACB=90°，AC=6，BC=8，∴AB=10 ∵点 D 是 AB 的中点，∴AD=DB=DC=5 ∵CD 是直径，∴∠CFD=90° ∴DF 是等腰△CDB 的中线，点 F 是 CB 的中点 ∵店 D 是 AB 的中点，∴DF 是△ABC 的中位线，DF=3 易知△FDG∽△BDF ∴퐹퐺 퐹퐷 = 퐹퐵 퐵퐷 解得：FG=12 5 例 2.如图，AB 是O 的直径，弦 CD 垂直平分半径 OA，AB=6，求 BC 的长。 【答案】：3√3 【解析】：如图，连接 AC，BC ∵AB=6，CE 垂直平分 OA ∴AE=EO=3 2 ，OB=3=CO，∠CEO=90° ∴在 RT△CEO 中，∠ECO=30°，∠COE=60° 同理，∠ACE=30°，∠CAE=60° ∴△ACO 是正三角形 ∴AC=AO=3 ∵AB 是直径，∴∠ACB=90° ∴BC=3√3 四、利用特殊角，构特殊三角形 解题技巧：特殊三角形主要指：①45°、45°、90°三角形，三边之比为 1：1：√2； ②30°、60°、90°三角形，三边之比为：1：√3：2。 要对着两种三角形边之间的关系烂熟于心。 例 1.如图，点 C 是O 的直径 BC 的延长线上的一点，CA 与O 相切于点 A，连接 AB。若 AB=AC， CD=2，求O 的半径。 【答案】：2 【解析】：如图，连接 AO ∵AB=AC，∴∠B=∠C ∵OA=OB=r，∴∠B=∠OAB ∵∠AOC=∠B+∠BAO，∴∠AOC=2∠B=2∠C ∵AC 是O 的切线，∴∠OAC=90° ∴∠AOC+∠C=90°，∴∠C=30°，∠AOC=60° 设O 的半径为 r，则 OA=OD=r ∵DC=2，∴OC=r+2 ∵△AOC 是直角三角形，且∠C=30°，∴2AO=OC，即：2r=r+2 解得：r=2 方法 4 利用切线的性质证明 一、证角度关系 解题技巧：“遇切线，连过亲切点的半径”，利用圆的有关性质转化线段与角度之间的关系。 例 1.如图，PA，PB 分别切O 于 A，B 两点，过劣弧퐴퐵̂ 上的一点 C 作O 的切线分别交 PA，PB 于点 D，E，求证：∠DOE=90°－1 2 ∠P 【答案】：见解析 【解析】：如图，连接 OA，OC，OB ∵AP、DC 是O 的切线，∴∠OAD=∠OCD=90° 又∵OD=OD，OA=OC ∴△ODA≌△ODC，∴∠AOD=∠COD 同理，∠COE=∠EOB ∴∠DOE=1 2 ∠퐴푂퐵 ∵在四边形 APBO 中，∠P+∠PBO+∠BOA+∠PAO=360°，∴∠P+∠AOB=180° ∴1 2 （∠P+∠AOB）=90°，1 2 ∠P+∠DOE=90° ∴∠DOE=90°－1 2 ∠P 例 2.如图，在△ABC 中，∠ABC=90°，点 D 是 AC 的中点，过 A，B，D 三点作O，交 CB 的延长线于 点 E，过点 E 作O 的切线交 AC 的延长线于点 F，求证：∠CEF+2∠F=90°。 【答案】：见解析 【解析】：如图，连接 DE，AE ∵∠ABC=90°，∴∠ABE=90° ∴AE 是直径，AE 过圆心 O ∴∠ADE=90° ∵点 D 是 AC 的中点，∴△ACE 是等腰三角形，AE=ED，∠AED=∠DEC，∠EAD=∠DCE ∵EF 是O 的切线，∴∠FEO=90° ∴在△AEF 中，∠F+∠FAE=90° ∵在△AED 中，∠DEA+∠DAE=90° ∴∠DEA=∠F，∴2∠F=∠CEA ∵∠CEA+∠CEF=90° ∴∠CEF+2∠F=90° 二、证线段关系 解题技巧：在圆中证线段关系，主要是平行关系和垂直关系，实质上还是通过基础图形转化角度来实现。 例 1.如图，△ABC 内接于O，AB 为O 的直径，∠ACB 的平分线交O 于 D，过 D 作O 的切线交 CA 的延长线于 E。求证：DE∥AB。 【答案】：见解析 【解析】：如图，连接 OD，BD ∵ED 是O 的切线，∴∠ODE=90° ∵AB 是O 的直径，∴∠ACB=90° ∵CD 是∠ACB 的角平分线，∴∠ACD=∠DCB=45° ∴∠ABD=∠ACD=45° ∵OD=OB，∴∠ODB=∠OBC=45° ∴∠BOD=90° ∴∠BOD=∠ODB=90° ∴AB∥ED 例 2.如图，△ABC 中，AB=AC，以 AB 为直径的O 交 BC 于点 D，过 D 作O 的切线交 AC 于 E，求 证：DE⊥AC。 【答案】：见解析 【解析】：如图，连接 OD ∵ED 是O 的切线，∴∠EDO=90° ∵AC=AB，∴∠C=∠B ∵OD=OB=r，∴∠B=∠ODB ∵∠CDE+∠EDO+∠ODB=180°，∴∠CDE+∠EDO+∠C=180° ∴AC∥DO 方法 5 切线与勾股定理（方程思想） 解题技巧：连切线，构造直角。剩下内容，与上一章方法 4 相同，利用方程思想结合勾股定理解题。 一、单勾股 例 1.如图，△ABC 中，AB=AC，O 为 AB 上一点，以 O 为圆心，OB 为半径的O 与 AC 切于点 E，与 BC 交于点 D，过 D 作O 的切线交 AC 于点 F，O 的半径为 3，CF=1。求 DC，AB 的长。 【答案】：DC=√10，AB=8 【解析】：如图连接 OE，OD ∵AC，DF 是O 的切线，∴∠AEO=∠ODF=90° ∵AB=AC，∴∠B=∠C ∵OB=OD=r，∴∠B=∠ODB，∴∠C=∠ODB ∴OD∥EF，∴∠EOD=90° ∴四边形 OEFD 是矩形，∠EFD=90° ∵EF=3，∴OD=EF=3=OE=DF=r ∵FC=1，∴在 Rt△DFC 中，DC=√10 设 AE=x，则 AC=x+3+1=x+4 ∵AB=AC，∴AO=x+4－r=x+1 在 Rt△AEO 中，푂퐸2 + 퐴퐸2 = 퐴푂2，即：32 + 푥2 = （푥 + 1）2 解得：x=4 ∴AB=AC=x+4=8 例 2.如图，在O 中，AB 为直径，퐴퐶̂ = 퐵퐶̂ ，弦 CF 与 OB 交于点 E，过点 F，A 分别作O 的切线交于 点 H，且 HF 与 AB 的延长线交于点 D。若 OA=2OE=4，求 AH 的长。 【答案】：AH=12 【解析】：如图，连接 OC，OF ∵DH，AH 是O 的切线 ∴∠OFD=∠OAH=90°，AH=FH ∵퐴퐶̂ = 퐵퐶̂ ，∴点 C 是퐵퐴̂ 的中点 ∵AB 是直径，∴CO⊥AB ∵OC=OF=r，∴∠OCE=∠OFE ∵∠ECO+∠CEO=90°，∠DFE+∠EFO=90°，∠DEF=∠CEO ∴∠DEF=∠DFE，∴DE=DF 设 DF=x，则 DO=x+2，FO=4 ∴在 Rt△DFO 中，푂퐹2 + 퐷퐹2 = 퐷푂2，即：42 + 푥2 = （푥 + 2）2 解得：x=3 设 FH=y，则 AH=y 在 Rt△DAH 中，퐷퐴2 + 퐴퐻2 = 퐷퐻2，即：92 + 푦2 = （3 + 푦）2 解得：y=12 ∴AH=12 二、双勾股 例 1.如图，△ABC 中，∠C=90°，点 C 在 AC 上，以 OA 为半径的O 交 AB 于点 D，E 为 BC 上一点， 且 DE=BE，连接 OD。若 AC=3，BC=4，OA=1，求 DE。 【答案】：DE=19 8 【解析】：如图，连接 OE ∵DE=EB，∴∠EDB=∠B ∵OA=OD=r，∴∠A=∠ODA ∵∠C=90°，∴∠A+∠B=90° ∴∠ADO+∠EDB=90°，∴∠ODE=90° 设 EB=x，则 ED=x，CE=4－x 在 Rt△COE 中，푂퐸2 = 푂퐶2 + 퐶퐸2，即푂퐸2 = 22 + （4 − 푥）2 在 Rt△ODE 中，푂퐸2 = 푂퐷2 + 퐷퐸2，即푂퐸2 = 12 + 푥2 即：푂퐸2 = 22 + （4 − 푥）2 = 푂퐸2 = 12 + 푥2 解得：x=19 8 ∴DE=19 8 例 2.如图，AB 是O 的直径，D 是O 上的一点，BC 为O 的切线（切点为 B）， OC∥AD，BA，CD 的 延长线交于点 E。若 EA=1，DA=2，DB=2ED，求O 的半径。 【答案】：√3 + 1 【解析】：如图，连接 OD，设 DB 与 OC 交于点 F ∵AB 是O 的直径，∴∠ADB=90° ∵OC∥AD，∴∠DFC=90° ∴根据垂径定理，DF=FB ∵FC=FC，∠DFC=∠CFB ∴△CFD≌△CFB ∴∠DCF=∠FCB，DC=CB ∵OD=OB ∴△COD≌△COB ∵CB 是O 的切线 ∴∠CDO=∠CBO=90° 设 OA=x 在 Rt△OED 中，퐷퐸2 = 푂퐸2 − 퐷푂2，即퐷퐸2 = （푥 + 1）2 − 푥2 在 Rt△ADB 中，퐷퐵2 = 퐴퐵2 − 퐷퐴2，即퐷퐵2 = （2푥）2 − 22 ∵DB=2DE，∴퐷퐵2 = 4퐷퐸2，即：（2푥）2 − 22 = 4[（푥 + 1）2 − 푥2] 解得：x=√3 + 1 方法 6 切割线图构矩形 解题技巧：如下图，AB 是O 的直径，CD 是O 的切线，AD⊥CD，AD 与O 交于点 E，连接 BE，连 接 OC 与 EB 交于点 G。过点 O 作 AD 的垂直线，交 AD 于点 F，过点 C 作 AB 的垂线，交 AB 于点 H。 则： ①OC∥AD（构造矩形 OFDC）； ②AC 平分∠BAD，퐶퐸̂ = 퐶퐵̂ （△COH≌△OAE）； ③OF=CD=EG=BG=CH，BH=DE=CG，OG=EF=AF=OH； ④AD+DE=AB， AE+AB=2AH=2AD； 以上几条结论主要通过构造矩形、构造全等，证垂直平分和全等，并结合圆的性质、勾股定理解决。 证明：∵AD⊥CD，DC 是O 的切线，作 OF⊥AD ∴∠FDC=∠DCO=∠OFD=90° ∴四边形 OFDC 是矩形（构造出矩形） ∴OC∥AD，OF=CD，∠FOC=90°，①得证； ∵∠FOA+∠FAO=90°，∠FOA+∠COB=90° ∴∠FAO=∠COH ∵∠AFO=∠CHO=90°，AO=OC=r ∴△COH≌△OAE ∴CH=OF=CD，∴AC 是∠BAD 的角平分线 ∴∠EAC=∠CAB，∴CE=CB，퐶퐸̂ = 퐶퐵̂ ，②全部得证； ∵AB 是O 的直径，∴BE⊥AD ∴BE∥CD ∴四边形 EGCD 和四边形 EGOF 是矩形（构造出 2 个小矩形） ∴EG=OF=CD，OC⊥BE ∵EC=CB，∴CO 是 EB 的垂直平分线 ∴EG=GB ∴OF=CD=EG=BG=CH 易证△COH≌△BOG，∴OH=OG ∴BH=CG=DE ∵OF⊥AE，且 OE=OA=r ∴OF 是 AE 的垂直平分线 ∴AF=EF ∴OG=EF=AF=OH，③全部得证； 易证△ADC≌△AHC，∴AG=AD ∴AD+DE=AB，AE+AB=2AH=2AD，④全部得证。 例 1.如图，已知 AB 是O 的直径，CD 是O 的切线，切点为点 D，퐴퐷̂ = 퐷퐸̂ ，BE⊥CD 于点 C，若 CD=4，BE=6，求 BD 的长。 【答案】：4√5 【解析】：如下图，过点 D 作 AB 的垂线，交 AB 于点 F，过点 O 作 CB 的垂线，交 AB 于点 G，连接 OE ∵CD 是O 的切线，DC⊥BC，OG⊥BC ∴∠ODC=∠DCG=∠CGO=90° ∴四边形 CDOG 是矩形 ∴OG=CD=4，∠DOG=90° ∵퐴퐷̂ = 퐷퐸̂ ∴∠ABD=∠DCE，∴BD 是∠ABC 的角平分线 ∵DF⊥AB，DC⊥BC ∴DF=DC=OG=4 ∵∠DOF+∠ODF=90°，∠DOF+∠GOB=90° ∴∠DOF=∠GOB ∵OD=OB，∠DFO=∠OGB=90° ∴△FDO≌△GOB，∴DF=OG=4 ∵OG⊥BE，OB=OE=r，BE=6 ∴OG 是 BE 的垂直平分线，EG=GB=3 ∴OF=3，∴OD=5=CG ∴CE=2，CB=2+3+3=8 ∴在 Rt△DCB 中，BD=4√5 例 2.如图，AC 是O 的直径，CD 是O 的弦，点 B 在O 上，且퐵퐷̂ = 퐵퐴̂ ，BE⊥CD 于点 E。 （1）求证：BE 是O 的切线； （2）若 AD=4，EC=1，求 BD 的长。 【答案】：（1）见解析 （2）BD=2√5 【解析】：（1）如下图，连接 BO 并延长，交 AD 于点 F，连接 AB，OD ∵퐵퐷̂ = 퐵퐴̂ ∴AB=BD ∵OA=OD=r，OB=OB ∴△OBA≌△OBD ∴∠OBA=∠OBD ∵BA=BD ∴BO⊥AD，即 OF⊥AD ∵BE⊥CD，AC 是O 的直径 ∴∠BFD=∠BED=∠EDF=90° ∴四边形 BEDF 是矩形 ∴∠EBF=90°，BF=ED，BE=FD ∴BE 是O 的切线 （2）∵AD=4 ∴根据垂径定理，AF=FD=2，∴BE=2 设 OF=x，则 CD=2x ∴ED=2x+1，∴BO=2x+1－x=x+1=AO ∴在 Rt△AOF 中，퐴퐹2 + 푂퐹2 = 퐴푂2，即22 + 푥2 = （푥 + 1）2 解得：x=3 2 ∴CD=3，∴ED=4 在 Rt△BED 中，BD=2√5 方法 7 双切线图 解题技巧：图中有多条切线时，常考虑切线长定理，同时结合角度的转化和中位线定理进行推导，基础图 形如下： 如图，AC 是O 的直径，PA、PB 是O 的切线，交O 于点 A、B，PB 与 AC 的延长线交于点 D，有 如下结论： ①PA=PB，OP⊥AB，퐴퐹̂ = 퐵퐹̂ ，AE=BE，∠APO=∠BPO=∠CAB=∠CBD； ②OE∥BC 且 2OE=BC（OE 是△ABC 的中位线）； 证明：∵AP、BP 是O 的切线 ∴根据切线长定理有如下结论 PA=PB，AP⊥AB，且 AE=BE，则퐴퐹̂ = 퐵퐹̂ ，∠APO=∠BPO ∵∠CAB+∠EAP=90°，∠EAP+∠APO=90° ∴∠CAB=∠APO ∵AC 是O 的直径 ∴∠ABC=90° ∵∠CBD+∠ABP=90°，∠ABP+∠BPO=90° ∴∠APD=∠BPO=∠CAB=∠CBD，①全部得证 ∵OE⊥AB，CB⊥AB，点 O 是 AC 的中点 ∴OE 是△ABC 的中位线 ∴OE∥BC 且 2OE=BC，②得证 例 1.如图，CA，CD 是是O 的切线，切点分别为 A，D，AB 是O 的直径，连接 AD。 （1）求证：∠C=2∠BAD； （2）若 AC=8，AB=12，求 AD 的长。 【答案】：（1）见解析 （2）AD=48 5 【解析】：（1）如图，连接 CO 交 AD 于点 M ∵CA、CD 是O 的切线 ∴根据切线长定理：∠CMA=90°，AM=MD，CA=CD，∠CAO=∠CDO=90°，∠ACO=∠DCO ∵∠DAO+∠CAD=90°，∠CAD+∠ACO=90° ∴∠DAO=∠ACO ∴∠ACD=2∠DAO （2）易知△ACM∽△OCA ∵AB=12，∴AO=6 ∵AC=8，∴CO=10 ∴퐴푀 퐴퐶 = 퐴푂 푂퐶 ，∴AM=24 5 ∴AD=48 5 例 2.如图，在△ABC 中，AB=AC，点 M 为△ABC 的内心，点 O 在 AB 上，O 经过 B，M 两点。 （1）求证：AM 与O 相切； （2）过点 A 作 AE 与O 相切于另一点 E，若 AB=10，BC=16，求 EM 的长。 【答案】：（1）见解析 （2）EM==16 3 【解析】：（1）如下图，连接 AM，BM，延长 AM 交 BC 于点 D ∵点 M 是△ABC 的内心 ∴AM 是∠BAC 的角平分线 ∵AB=AC ∴AD⊥BC ∵点 M 是△ABC 的内心 ∴∠ABM=∠MAD ∵∠AOM=2∠ABM ∴∠AOM=∠ABC ∴OM∥BD ∴OM⊥AD ∴AM 是O 的切线 （2）如上图，连接 OE,EM 与 AO 的交点为点 F 根据切线长定理：EM⊥AO，且 EF=FM ∵点 M 是△ABC 的内心 ∴DM=FM=FE=x ∵AB=10，∴AC=10 ∵BC=16，∴BD=DC=8=BF ∴AD=6，AM=6－x，FA=10－8=2 在 Rt△AFM 中，퐴퐹2 + 퐹푀2 = 퐴푀2，即22 + 푥2 = 퐴푀2 ∴22 + 푥2 = （6－x）2 解得：x=8 3 ∴EM=16 3 三、典型题型 题型 1 点与圆的位置关系（d 与 r） 解题技巧：点的圆的位置关系，一般用 d 与 r 的大小来判定。判断位置关系，关键点就是求解出点与圆心的 距离，然后和 r 比较来判断位置关系。 例 1.如图，已知矩形 ABCD 的边 AB=3，BC=4。 （1）以点 A 为圆心，4 为半径作A，则点 B，C，D 与A 的位置关系如何？ （2）若以点 A 为圆心作A，是 B，C，D 三点中至少有一点在A 内，且至少有一点在A 外，求A 的半径 r 的取值范围。 【答案】：（1）B 在圆内，C 在圆外，D 在圆上； （2）3＜r＜5 【解析】：（1）r=4 ∵AB=3＜r，∴点 B 在圆内； ∵AC=5＞r，∴点 C 在圆外； ∵AD=4=r，∴点 D 在圆上 （2）∵AB=3，AD=4，AC=5 要使一点在圆内，则这点必定是点 B，即 r＞3 要使一点在圆外，则这点必定是点 C，即 r＜5 ∴3＜r＜5 例 2.如图，坐标原点在O’上，点 O’的坐标为（1，1），试判断点 P（－1，1），点 Q（1，0），点 R（2， 2）与O’的位置关系。 【答案】：点 P 在圆外，点 Q 在圆内，点 R 在圆上 【解析】：r=OO’=√2 ∵O’P=2＞r，∴点 P 在圆外； ∵O’Q=1＜r，∴点 Q 在圆内； ∵O’R=√2=r，∴点 R 在圆上 题型 2 直线与圆的位置关系（d 与 r） 解题技巧：直线和圆的位置有三种：相交、相切和相离，判断方法有两种： 方法一：根据直线与圆的交点个数判定：{ 两个交点：相交 一个交点：相切 无交点：相离 方法二：根据直线和圆心距离d与半径r大小关系判定：{ d＜r，相交 d = r，相切 d＞r，相离 例1.圆的直径是13cm，如果圆心与直线上某一点的距离是6.5cm，那么该直线和圆的位置关系是（ ） A．相离 B．相切 C．相交 D．相交或相切 【答案】：D 【解析】：圆的直径为13cm，则半径为6.5cm，存在两种情况，如下图： 如图一，则直线与圆心的距离为6.5，则为相切关系 如图二，则直线与圆心的距离小于6.5，则为相交关系 综上得，答案为D 例2.已知⊙O的半径等于8cm，圆心O到直线l的距离为9cm，则直线l与⊙O的公共点的个数为（ ） A．0 B．1 C．2 D．无法确定 【答案】：A 【解析】：∵圆心与直线距离d=9＞半径r=8 ∴直线与圆的位置关系为相离 ∴交点个数为0个，选A 题型 3 切线的性质与判定 解题技巧：切线的性质：切点与圆心的连线与切线垂直 切线的判定：①连接圆心与切点，证与切线垂直；②过圆心作垂线，证长度为 r 例 1.如图，AB 是O 的弦，AD 的延长线与过点 B 的O 的切线交于点 C，若∠A=20°，求∠C 的大小。 【答案】：50° 【解析】：如下图，连接 OB ∵OA=OB=r，∠A=20° ∴∠ABO=20° ∵BC 是O 的切线 ∴∠OBC=90° ∴∠C=50° 例 2.如图，已知 AB 是O 的直径，BC 是O 的切线，切点为 B，OC 平行于弦 AD，求证：DC 是O 的 切线。 【答案】：见解析 【解析】：如下图，连接 OD ∵AD∥OC ∴∠DAO=∠COB，∠ADO=∠DOC ∵AO=OD=r ∴∠DAO=∠COB=∠ADO=∠DOC ∵OD=OB=r，OC=OC ∴△ODC≌△OBC ∵BC 是O 的切线，∴∠OBC=90° ∴∠ODC=90° ∴DC 是O 的切线 题型 4 切线长定理 解题技巧：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹 角，且使得左右两边的图形完全对称。 例 1.如图，PA，PB，CD 切O 于点 A，B，E，若 AC=2，BD=3，PA=5，求 CD 的长和△PCD 的周长。 【答案】：CD=5，△PCD 的周长=10 【解析】：根据切线长定理，DE=DB，EC=AC ∴DE=3，EC=2，∴CD=5 ∵△PCD 的周长=PC+PD+CD=PC+CE+PD+ED=PA+PB 又∵PA=5 ∴△PCD 的周长=5+5=10 例 2.如图，CA，CB 是O 的切线，切点分别是 A，B，若果O 的半径为 2√3，AB=6，求∠ACB 的大 小。 【答案】：60° 【解析】：如下图，连接 OA，OB，连接 OC 与 AB 交于点 D ∵CA，CB 是O 的切线 ∴根据切线长定理：AB⊥OC，且 AD=DB ∵半径为 2√3，即 OB=2√3 ∵AB=6，∴BD=3 ∴在 Rt△ODB 中，OB=2√3，BD=3，则 OD=√3 ∴∠OBD=30°，∠BOD=60° ∴∠BCO=30° ∴∠ACB=60° 题型 5 三角形的内心和外心 解题方法：此类题型，需要抓住三角形内心和外心的特点。 ①三角形内心：三角形内切圆圆心，即三角形角平分线的交点，内心到三边的距离相等 ②三角形外心：三角形外接圆圆心，即三角形垂直平分线交点，外心到三顶点距离相等。 例 1.已知一个三角形的三边长分别为 5、7、8，则其内切圆的半径为（ ） A.√3 2 B.3 2 C.√3 D.2√3 【答案】：C 【解析】：如图 1，设 AB=5，AC=7，BC=8，作 BC 的垂线 AD 交 BC 于点 D。如图 2，连接内切圆圆心与 三条切线的切点 OE，OF，OG 设 DC 长为 x，则 BD=（8－x） 在直角三角形 ABD 与直角三角形 ADC 中，满足：√퐴퐵2 − 퐵퐷2 = √퐴퐶2 − 퐶퐷2，即： √52 − （8 − x）2 = √72 − 푥2 解得：x=11 2 在直角三角形 ADC 中，根据勾股定理，AD=√72 − （ 11 2 ）2 =5√3 2 ∴푆△퐴퐵퐶 = 1 2 × 8 × 5√3 2 =10√3 在图 2 中，设圆心 O 到三边的距离为 h ∵푆△퐴퐵퐶 = 푆△퐴퐵푂 + 푆△퐴푂퐶 + 푆△푂퐵퐶 ∴10√3 = 1 2 × 5 × ℎ + 1 2 × 7 × ℎ + 1 2 × 8 × ℎ 化简得：10√3 = 10ℎ 解得：h=√3 例 2.如图，△ABC 内接与⊙O，AB=AC，CO 的延长线交 AB 于点 D 求证：AO 平分∠BAC； 【答案】：见解析 【解析】：∵⊙O 是△ABC 的外接圆 ∴点 O 是△ABC 角平分线的交点 ∴AO 平分∠BAC 例3.如图，△ABC的内切圆与三边分别相切于点D、E、F 则下列等式：①∠EDF＝∠B；②2∠EDF＝∠A＋∠C；③2∠A＝∠FED＋∠EDF ；④∠AED＋∠BFE＋ ∠CDF＝180°，其中成立的个数是（ ） A．1个 B．2个 C．3个 D．4个 【答案】：B 【解析】：如下图，连接OE，OF，OD，OA，OB，OC ∵圆 O 是三角形 ABC 的内切圆 ∴OE⊥AB，OF⊥BC，OD⊥AC ∴∠BEO=∠OFB=90° ∴在四边形 BEOF 中∠B+∠EOF=180° ∵2∠EDF=∠EOF ∴∠B+2∠EDF=180° ∵∠A+∠C+∠B=180° ∴∠A+∠C=2∠EDF ∴②正确 同理，①、③错误 在△AOE 与△AOD 中 { ∠퐴퐸푂 = ∠퐴퐷푂 = 90° 퐸푂 = 푂퐷 퐴푂 = 퐴푂 ∴△AED≌△ADO ∴AE=AD 同理，BE=BF，DC=FC ∵∠AED+∠ADE+∠BAC=∠FDC+∠DFC+∠FCD=∠EFB+∠FEB+∠EBF=180° ∴∠AED+∠ADE+∠FDC+∠DFC+∠EFB+∠FEB=180°×3－（∠BAC+∠FCD+∠EBF） ∴2（∠AED＋∠BFE＋∠CDF）=360° ∠AED＋∠BFE＋∠CDF=180° ∴④正确