人教版九年级数学上册第24章测试题含答案 13页

九上数学第二十四章检测题(RJ)‎ ‎(考试时间：120分钟　　　　满分：120分)‎ 第Ⅰ卷(选择题　共36分)‎ 一、选择题(共12小题，每小题3分，共36分)‎ ‎1．下列说法中，正确的是 (　B　)‎ A．等弦所对的弧相等 B．等弧所对的弦相等 C．圆心角相等，所对的弦相等 D．弦相等所对的圆心角相等 ‎2．(杭州中考)圆内接四边形ABCD中，已知∠A＝70°，则∠C＝(　D　)‎ A．20° B．30° C．70° D．110°‎ ‎3．(青岛中考)如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED＝20°，则∠BCD的度数为 (　B　)‎ A．100° B．110° C．115° D．120°‎ ‎,第3题图)　　　,第4题图)　　　,第5题图)　‎ ‎4．如图，⊙O的直径AB垂直于弦CD，垂足为点E，∠A＝22.5°，OC＝4，则CD的长为 ‎ ‎(　C　)‎ A．2 B．4 C．4 D．8‎ ‎5．如图，∠O＝30°，C为OB上一点，且OC＝6，以点C为圆心，半径为3的圆与OA位置关系是 (　C　)‎ A．相离 B．相交 C．相切 D．以上均有可能 ‎6．正六边形的每一个内角都相等，则其中一个内角α的度数是(　B　)‎ A．240° B．120° C．60° D．30°‎ ‎7．(齐齐哈尔中考)一个圆锥的侧面积是底面积的3倍，则这个圆锥侧面展开图的圆心角度数为 (　A　)‎ A．120° B．180° C．240° D．300°‎ ‎8．(日照中考)如图，AB是⊙O的直径，PA切⊙O于点A，连接PO并延长交⊙O于点C，连接AC，AB＝10，∠P＝30°，则AC的长度是 (　A　)‎ A．5 B．5 C．5 D. 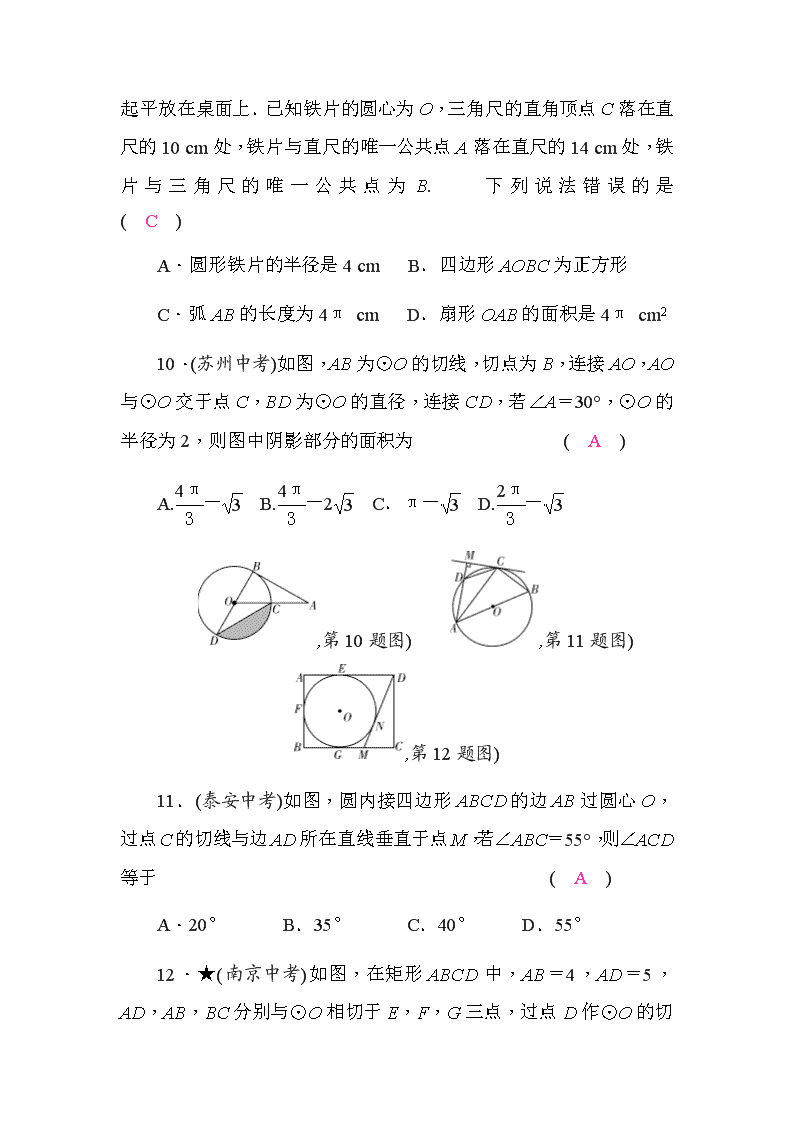‎,第8题图)　　,第9题图)‎ ‎9．(宜昌中考)如图，‎ 圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上．已知铁片的圆心为O，三角尺的直角顶点C落在直尺的10 cm处，铁片与直尺的唯一公共点A落在直尺的14 cm处，铁片与三角尺的唯一公共点为B.下列说法错误的是 (　C　)‎ A．圆形铁片的半径是4 cm B．四边形AOBC为正方形 C．弧AB的长度为4π cm D．扇形OAB的面积是4π cm2‎ ‎10．(苏州中考)如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A＝30°，⊙O的半径为2，则图中阴影部分的面积为 (　A　)‎ A.－ B.－2 C．π－ D.－ ‎,第10题图)　　,第11题图)　　,第12题图)‎ ‎11．(泰安中考)如图，圆内接四边形ABCD的边AB过圆心O，过点C的切线与边AD所在直线垂直于点M，若∠ABC＝55°，则∠ACD等于 (　A　)‎ A．20° B．35° C．40° D．55°‎ ‎12．★(南京中考)如图，在矩形ABCD中，AB＝4，AD＝5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O 的切线交BC于点M，切点为N，则DM的长为 (　A　)‎ A. B. C. D．2 第Ⅱ卷(非选择题　共84分)‎ 二、填空题(本大题共6小题，每小题3分，共18分)‎ ‎13．在⊙O中，直径为10 cm，PO＝4.8 cm，则点P与⊙O的位置关系是__点P在⊙O内__．‎ ‎14．如图，已知⊙O的半径为4，OC垂直弦AB于点C，∠AOB＝120°，则弦AB的长为__4__．‎ ‎,第14题图)　　　　,第15题图)‎ ‎15．(烟台中考)如图，△ABC的外心坐标是__(－2，－1)__．‎ ‎16．(天津中考)如图，△ABC是⊙O的内接三角形，AB为⊙O的直径，点D为⊙O上一点，若∠CAB＝55°，则∠ADC的大小为__35°__．‎ ‎,第16题图)　　　,第17题图)　　　,第18题图)‎ ‎17．(南京中考)如图，在⊙O的内接五边形ABCDE中，∠CAD＝35°，则∠B＋∠E＝__215__°.‎ ‎18．★(陕西中考)如图，AB是⊙O的弦，AB＝6，点C是⊙O上的一个动点，且∠ACB＝45°.若点M，N分别是AB，BC的中点，则MN长的最大值是__3__．‎ 三、解答题(本大小题共8小题，共66分)‎ ‎19．(6分)如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB.‎ ‎(1)若CD＝16，BE＝4，求⊙O的直径；‎ ‎(2)若∠M＝∠D，求∠D的度数．‎ 解：(1)∵CD⊥AB，AB是直径，‎ ‎∴CE＝DE，在Rt△OED中，设⊙O的半径为r.‎ 则r2＝82＋(r－4)2，∴r＝10，‎ ‎∴⊙O的直径为20；‎ ‎(2)∵∠M＝∠BOD，又∵∠D＝∠M，‎ ‎∴∠EOD＋∠D＝2∠D＋∠D＝3∠D＝90°，∴∠D＝30°.‎ ‎20．(6分)如图所示，已知△ABC内接于⊙O，∠C＝45°，点O到弦AB的距离OD＝2，求：‎ ‎(1)弦AB的长；‎ ‎(2)弦AB所对的劣弧的长．‎ 解：(1)连接OA，OB，∴∠AOB＝2∠C＝90°.∵OA＝OB，OD⊥AB，‎ ‎∴OD是AB边上的中线，∴Rt△AOB中，OD＝AD＝BD＝AB，∴AB＝2OD＝4.‎ ‎(2)OA＝＝＝2.‎ ‎∵所对的圆心角∠AOB＝90°，‎ ‎∴的长为·π·OA＝·π·2＝π.　‎ ‎21．(8分)如图，在菱形ABCD中，点P在对角线AC上，且PA＝PD，⊙O是△PAD的外接圆，求证：AB是⊙O的切线．‎ 证明：连接OP，OA，OP交AD于E，∵PA＝PD，‎ ‎∴弧AP＝弧DP，∴OP⊥AD，‎ ‎∴AE＝DE，∵OP＝OA，‎ ‎∴∠OAP＝∠OPA，过E作EF⊥AP交AP于F，∵PA＝PD，∴∠DAP＝∠ADP，‎ ‎∵∠DAP＝∠AOP，∠AOF＝∠AOP，‎ ‎∴∠DAP＝∠AOF，∵∠OAP＋∠AOF＝90°，‎ ‎∴∠DAP＋∠OAP＝90°，∵四边形ABCD为菱形，‎ ‎∴∠DAP＝∠CAB，∴∠CAB＋∠OAP＝90°，‎ ‎∴OA⊥AB，∴直线AB与⊙O相切．　‎ ‎22．(8分)如图，一个圆锥的高为3 cm，侧面展开图是半圆．求：‎ ‎(1)圆锥的母线长与底面半径之比；‎ ‎(2)求∠BAC的度数；‎ ‎(3)圆锥的侧面积(结果保留π)．‎ 解：(1)设此圆锥的高为h，底面半径为r，母线长AC＝l.∵2πr＝πl，∴＝2.‎ ‎∴圆锥的母线长与底面半径之比为2∶ 1.‎ ‎(2)∵＝2，∴圆锥高与母线的夹角为30°，则∠BAC＝60°.‎ ‎(3)由图可知l2＝h2＋r2，h＝3 cm，∴(2r)2＝(3)2＋r2，即4r2＝27＋r2，‎ 解得r＝3 cm，∴l＝2r＝6 cm.∴圆锥的侧面积为＝18π cm2.　‎ ‎23.(8分)(宜昌中考)已知，四边形ABCD中，E是对角线AC上一点，DE＝EC，以AE为直径的⊙O与边CD相切于点D，B点在⊙O上，连接OB.‎ ‎(1)求证：DE＝OE；‎ ‎(2)若CD∥AB，求证：四边形ABCD是菱形．‎ 证明：(1)如图，连接OD，‎ ‎∵CD是⊙O的切线，∴OD⊥CD，‎ ‎∴∠2＋∠3＝∠1＋∠COD＝90°，‎ ‎∵DE＝EC，∴∠1＝∠2，‎ ‎∴∠3＝∠COD，∴DE＝OE；‎ ‎(2)∵OD＝OE，∴OD＝DE＝OE，∴∠3＝∠COD＝∠DEO＝60°，∴∠2＝∠1＝30°，∵OA＝OB＝OE，OE＝DE＝EC，∴OA＝OB＝DE＝EC，∵AB∥CD，∴∠4＝∠1，∴∠1＝∠2＝∠4＝∠OBA＝30°，∴△ABO≌△CDE，∴AB＝CD，∴四边形ABCD是平行四边形，∴∠DAE＝∠DOE＝30°，∴∠1＝∠DAE，∴CD＝AD，‎ ‎∴四边形ABCD是菱形．　‎ ‎24．(10分)(天津中考)已知A，B，C是⊙O上的三个点，四边形 OABC是平行四边形，过点C作⊙O的切线，交AB的延长线于点D.‎ ‎(1)如图①所示，求∠ADC的大小；‎ ‎(2)如图②所示，经过点O作CD的平行线，与AB交于点E，与交于点F，连接AF，求∠FAB的大小．‎ 解：(1)∵CD是⊙O的切线，C为切点，∴OC⊥CD，即∠OCD＝90°.∵四边形OABC是平行四边形，∴AB∥OC，即AD∥OC.‎ ‎∴∠ADC＋∠OCD＝180°，∴∠ADC＝180°－∠OCD＝90°.‎ ‎(2)如图，连接OB，则OB＝OA＝OC.∵四边形OABC为平行四边形，∴OC＝AB.∴OA＝OB＝AB.即△AOB是等边三角形．于是∠AOB＝60°.由OF∥CD，又∠ADC＝90°，得∠AEO＝∠ADC＝90°.‎ ‎∴OF⊥AB.∴＝.∴∠FOB＝∠FOA＝∠AOB＝30°.‎ ‎∴∠FAB＝∠FOB＝15°.　‎ ‎25.(10分)(凉山州中考)如图，已知AB为⊙O的直径，AD，BD是⊙O的弦，BC是⊙O的切线，切点为B，OC∥AD，BA，CD的延长线相交于点E.‎ ‎(1)求证：DC是⊙O的切线；‎ ‎(2)若AE＝1，ED＝3，求⊙O的半径．‎ ‎(1)证明：连接DO.∵AD∥OC，‎ ‎∴∠DAO＝∠COB，∠ADO＝∠COD，‎ 又∵OA＝OD，∴∠DAO＝∠ADO，‎ ‎∴∠COD＝∠COB.在△COD和△COB中，‎ ‎∵OD＝OB，OC＝OC，∴△COD≌△COB(SAS)，‎ ‎∴∠CDO＝∠CBO.‎ ‎∵BC是⊙O的切线，∴∠CBO＝90°，∴∠CDO＝90°，‎ 又∵点D在⊙O上，∴CD是⊙O的切线；‎ ‎(2)解：设⊙O的半径为R，则OD＝R，OE＝R＋1，‎ ‎∵CD是⊙O的切线，∴∠EDO＝90°，‎ ‎∴ED2＋OD2＝OE2，∴32＋R2＝(R＋1)2，解得R＝4.‎ ‎∴⊙O的半径为4.　‎ ‎26．(10分)(兰州中考)如图，在Rt△ABC中，∠C＝90°，∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O，使⊙O经过点A和点D.‎ ‎(1)判断直线BC与⊙O的位置关系，并说明理由；‎ ‎(2)若AC＝3，∠B＝30°，‎ ‎①求⊙O的半径；‎ ‎②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的面积．(结果保留根号和π)‎ ‎　解：(1)相切，理由如下：‎ 如图，连接OD，∵AD平分∠BAC，‎ ‎∴∠1＝∠2.∵OA＝OD，∴∠1＝∠3，‎ ‎∴∠2＝∠3，∴OD∥AC.‎ 又∵∠C＝90°，∴OD⊥BC，∴BC与⊙O相切．‎ ‎(2)①∵AC＝3，∠B＝30°，∴AB＝6.设OA＝OD＝r，∴OB＝2r，∴2r＋r＝6，解得r＝2，即⊙O的半径是2.‎ ‎②由①得OD＝2，即OB＝4，BD＝2，‎ S阴影＝× 2× 2－＝2－.　‎