苏科版九年级上期中考试数学试题（苏教版九年级数学上册期中考试检测试剂） 5页

苏教版九年级数学上册期中考试测试题 （满分 150 分 时间 120 分） 一、选择题（每题 3 分，共 18 分） 1. 在 1:5000 的地图上，A、B 两地的图上距离为 3cm，则 A、B 两地间实际距离为（ ） A．15m B．150m C．1500m D．15000m 2. 数据 1、2、4、4、3 的众数是（ ） A. 1 B. 2 C. 3 D. 4 3. 两个相似三角形的周长比为 1∶4，则它们的对应边上的高比为（ ） A. 1∶2 B. 1∶4 C. 1∶8 D. 1∶16 4. 已知点 C 是线段 AB 的黄金分割点，且 AC＞BC，则下列等式成立的是（ ） A. AC2=BC·AB B. AC2=2BC·AB C. AB2=AC·BC D. BC2=AB·AC 5. 如图，在□ABCD 中，点 E 为 AD 的中点，连接 BE 交 AC 于点 F，则 AF∶CF= （ ） A. 1∶2 B. 1∶3 C. 2∶3 D. 2∶5 6. 有一人患流感，经过两轮传染后，共有 121 人患上了流感，那么每轮传染中，平均 一个人传染的人数为（ ） A. 8 人 B. 9 人 C. 10 人 D. 11 人 二、填空题（每题 3 分，共 30 分） 7. 如果 2 3 x y ，则 x x y = . 8. 如图，O 为△ABC 的重心，若 OD=2，则 AO= . 9. 若分式 2 1 x x x   的值为 0，则 x= . 10. 如图，已知圆内接四边形 ABCD 中，弧 BAD 的度数为 140°， 则∠BAD= 度. 11. 若 0132  xx ，则 862 2  xx = . 12. 一组数据 4、0、1、  2、2 的平均数为 . 13. 一直角三角形的两条直角边长分别为 6 和 8，则它的内切圆半径为 . 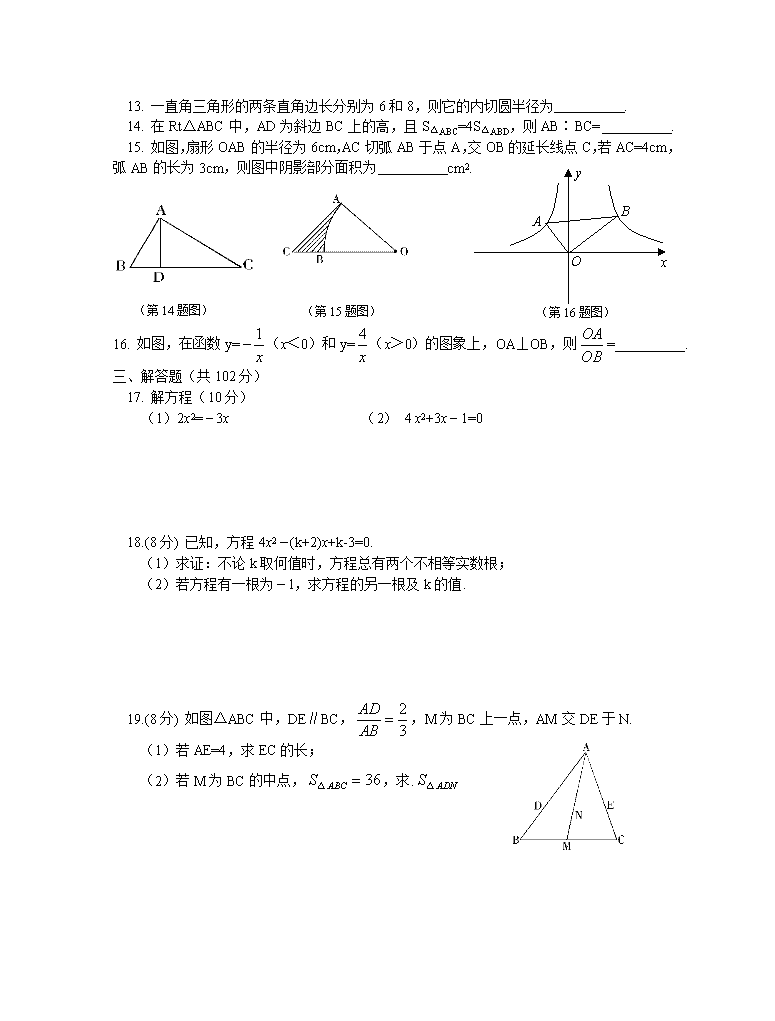A D CB E F （第 5 题图） （第 8 题图） （第 10 题图） 14. 在 Rt△ABC 中，AD 为斜边 BC 上的高，且 S△ABC=4S△ABD，则 AB∶BC= . 15. 如图，扇形 OAB 的半径为 6cm，AC 切弧 AB 于点 A，交 OB 的延长线点 C，若 AC=4cm， 弧 AB 的长为 3cm，则图中阴影部分面积为 cm2. 16. 如图，在函数 y= 1 x  （x＜0）和 y= 4 x （x＞0）的图象上，OA⊥OB，则 OA OB = . 三、解答题（共 102 分） 17. 解方程（10 分） （1）2x2=  3x （2） 4 x2+3x  1=0 18.(8 分) 已知，方程 4x2  (k+2)x+k-3=0. （1）求证：不论 k 取何值时，方程总有两个不相等实数根； （2）若方程有一根为  1，求方程的另一根及 k 的值. 19.(8 分) 如图△ABC 中，DE∥BC， 2 3 AD AB  ，M 为 BC 上一点，AM 交 DE 于 N. （1）若 AE=4，求 EC 的长； （2）若 M 为 BC 的中点， 36ABCS△ ，求. ADNS△ （第 15 题图）（第 14 题图） x y O BA （第 16 题图） 20.(8 分) 某篮球队在一次联赛中共进行了 10 场比赛，已知 10 场比赛的平均得分为 88 分，且前 9 场比赛的得分依次为：97、91、85、91、84、86、85、82、88. （1）求第 10 场比赛的得分； （2）求这 10 场比赛得分的中位数，众数和方差. 21.(8 分) 如图，AB 是⊙O 的切线，切点为 B ，直线 AO 交⊙O 于点 C、D，若 ∠A=30°. （1）求∠D 的度数; （2）过 C 点作⊙O 的切线交 AB 于 E，若 CE=2，求⊙O 的半径. 22.(10 分) 如图，Rt△ABC 中，∠ACB=90°，D 是 BC 的中点，CE⊥AD，垂足为 E. （1）求证：CD2=DE·AD； （2）求证：∠BED=∠ABC. 23.(10 分)矩形 ABCD 中，AB=6 cm BC=12 cm ，点 P 从 A 出发，沿 AB 边以 1cm/s 的速度 向点 B 匀速移动，同时点 Q 从点 B 出发，沿 BC 边以 2cm/s 的速度向点 C 匀速移动，设运 动时间为 t s. （1）t 为何值时，△DPQ 的面积等于 28cm2； （2）若 DQ⊥PQ 时，求 t 的值； 24.(12 分) 泰州凤凰城二日游，旅游信息： 旅游人数 收费标准 不超过 30 人 人均收费 800 元 超过 30 人 每增加 1 人，人均收费降低 10 元，但人均收 费不低于 500 元。 根据此旅游信息：某公司组织一批员工到该风景区旅游，支付给旅行社 28000 元. （1）你能确定参加这次旅游的人数吗？ （2）若该公司又组织第二批员工到凤凰城旅游并支付给旅行社 29250 元。如果这两批 员工一次性去旅游，则该公司可节约旅游费用多少元？ 25.(12 分)如图，在⊙O 中，AD∥BC，AC⊥BD 垂足为 E。 （1）求证：BE=CE； （2）若 AD=4，M 为 AD 的中点，延长 ME 交 BC 于 F， ①判断 EF 与 BC 的位置关系； ②求 OF 的长度。 A B CD P Q 26.(14 分) 已知⊙O 的半径为 2，∠AOB=120°。 （1）点 O 到弦 AB 的距离为 . （2）若点 P 为优弧 AB 上一动点（点 P 不与 A、B 重合），设∠ABP=α，将△ABP 沿 BP 折叠，得到 A 点的对称点为 A＇； ①若∠α=30°，试判断点 A＇与⊙O 的位置关系； ②若 BA＇与⊙O 相切于 B 点，求 BP 的长； ③若线段 BA＇与优弧 APB 只有一个公共点，直接写出α的取值范围.