第1章 第4节 相对运动-2021年初中物理竞赛及自主招生大揭秘专题突破 13页

第四节 相对运动 研究一个物体的运动时，总要选择一个参照物作为标准。很多问题中的参照物就是我们认为静 止的地面。在一些问题中，我们也需要选择其他运动着的物体作为参照物，这样会使得解决问题更 加方便快捷。 一、共线的两个物体的相对运动 在同一直线上运动的 A ， B 两个物体，其相对运动又分为两种情况： (1)如图 3.51 所示，若两者同向运动，其中 B 物体相对于 A 物体的运动速度 B AB Av v v 对 ，若 B Av 对 为正，则 B 离 A 越来越远，反之， B 离 A 越来越近。 (2)如图3.52所示，若两者反向运动，其中 B 物体相对于 A 物体的运动速度 B AB Av v v 对 。 上述相对速度的计算也可以将表示 A ，B 两物体速度的有向线段的起点画在同一点，则从 Av 的 末端指向 Bv 末端的有向线段就表示 B Av 对 ，如图 3.53 所示例子。 例 1 一条船逆流而上航行，已知河水流速为 0v ，船在静水中的速度为 1v 。船行至靠近岸边的 A 处时一只木箱子掉入水中，直至 0t 时间后被船员发现，于是船立即掉头寻找箱子，并于靠近岸边 B 处将箱子捞起。不计船掉头所需的时间，河道笔直，求 A ， B 之间的距离。 分析与解 船在静水中的速度 1v 并不是船相对于地面的速度，而是指船相对于河水的速度，下 面我们分别以地面和河水为参照物，来求解这个问题。 (1)以地面为参照物。船逆流而上时对地速度为 1 0v v ，掉 头后顺流而下对地的速度为 1 0v v ，木箱顺水漂流对地速度为 0v ，画出船及木箱的运动示意图如图 3.54 所示。从木箱掉落的O 处到 A 处，船向上游前进了  1 0 0OAs v v t  的距离，设从船掉 头 到 追 上 木 箱 用 时 1t ， 则 船 追 赶 箱 子 向 下 游 前 进 了 距 离  1 0 1ABs v v t  。从木箱掉落到被捞起，木箱向下游移动的距离为  0 0 1OBs v t t  ，则有      1 0 0 0 0 1 1 0 1v v t v t t v v t     ， 解 得 1 0t t ， 因 此 A ， B 之 间 的 距 离 为    1 0 1 1 0 0ABs v v t v v t    。 (2)以河水为参照物。无论船向上游还是向下游行驶，相对于河水的速度大小总是 1v ，而相对于 水，木箱保持静止，因此，船在木箱落水后 0t 时间返回，则一定又经过 0t 时间找到木箱，从船返回 到找到木箱这个过程，船对地移动的距离即为  1 1 0ABs v v t  。 由本题可以看出，选择合适的参照物往往可以使解决问题变得更简便，甚至使得看起来无从下 手的问题也轻而易举就得到解决。如果参照物选择不当就会适得其反，需要同学们多总结、多思考。 例 2 商场中有一自动扶梯，某顾客以相对扶梯的速度 1v 沿开动上行的扶梯走上楼时，数得走 了 1 16N  级，当他用同样的速度相对扶梯沿向下开动的自动扶梯走上楼时，数得走了 2 48N  级， 已知自动扶梯向上、向下运行的速度大小恒为 0v ，问： 1v ， 0v 的比值为多少？静止时自动扶梯露出 的级数为多少？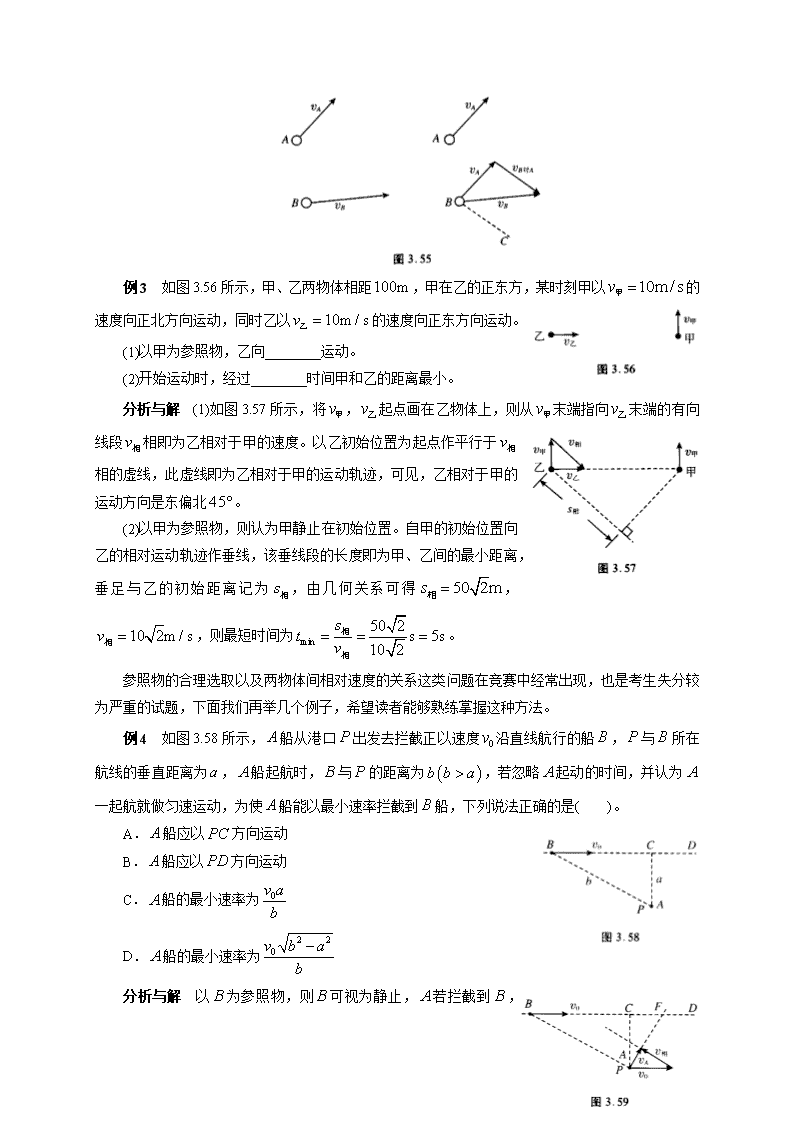 分析与解 人沿着扶梯上行时，人相对扶梯的速度为 1v ，则人对地的速度为 0 1v v ，设扶梯露 出的级数为 0N ，每一级长度为l ，则人上行的时间为 0 1 0 1 N lt v v   ，人“数得”的扶梯级数相当于是 人相对扶梯走过的距离，因此有 0 1 1 1 1 0 1 N lN l v t vv v    ① 人沿着扶梯下行时，人对地的速度为 1 0v v ，则人下行的时间为 0 2 1 0 N lt v v   ，因此 0 2 1 2 1 1 0 N lN l v t vv v    ② 联立①②两式可得 1 2 1 0 2 1 2v N N v N N   ， 0 24N  二、不共线的两个物体的相对运动 如图 3.55 所示，当两个物体速度方向不共线时，我们仍将表示 A ，B 两物体速度的有向线段的 起点画在同一点，则从 Av 的末端指向 Bv 末端的有向线段就表示 B 对 A 的相对速度 B Av 对 ，自 B 点画 虚线 BC 平行于 B Av 对 ，则 BC 就是 B 相对于 A 的运动路线，即以 A 为参照物时，B 的速度为 B Av 对 ， 运动路线为 BC 直线。 例 3 如图 3.56 所示，甲、乙两物体相距100m ，甲在乙的正东方，某时刻甲以 10m / sv 甲 的 速度向正北方向运动，同时乙以 10m / sv 乙 的速度向正东方向运动。 (1)以甲为参照物，乙向________运动。 (2)开始运动时，经过________时间甲和乙的距离最小。 分析与解 (1)如图 3.57 所示，将 v甲 ， v乙 起点画在乙物体上，则从 v甲 末端指向 v乙 末端的有向 线段 v相 相即为乙相对于甲的速度。以乙初始位置为起点作平行于 v相 相的虚线，此虚线即为乙相对于甲的运动轨迹，可见，乙相对于甲的 运动方向是东偏北 45。 (2)以甲为参照物，则认为甲静止在初始位置。自甲的初始位置向 乙的相对运动轨迹作垂线，该垂线段的长度即为甲、乙间的最小距离， 垂足与乙的初始距离记为 s相 ，由几何关系可得 50 2ms 相 ， 10 2m / sv 相 ，则最短时间为 min 50 2 s 5s 10 2 st v   相 相 。 参照物的合理选取以及两物体间相对速度的关系这类问题在竞赛中经常出现，也是考生失分较 为严重的试题，下面我们再举几个例子，希望读者能够熟练掌握这种方法。 例 4 如图 3.58 所示， A 船从港口 P 出发去拦截正以速度 0v 沿直线航行的船 B ， P 与 B 所在 航线的垂直距离为 a ，A 船起航时，B 与 P 的距离为  b b a ，若忽略 A 起动的时间，并认为 A 一 起航就做匀速运动，为使 A 船能以最小速率拦截到 B 船，下列说法正确的是( )。 A． A 船应以 PC 方向运动 B． A 船应以 PD 方向运动 C． A 船的最小速率为 0v a b D． A 船的最小速率为 2 2 0v b a b  分析与解 以 B 为参照物，则 B 可视为静止， A 若拦截到 B ， 则 A 相对于 B 的运动轨迹必为 AB 连线，即 A 对 B 的相对速度 v相 的方向应由 A 指向 B 。将 B 船的 速度 0v 画在 A 上，以 0v 的末端为起点作 AB 连线的平行线如图 3.59 所示，则该平行线的方向即为 v相 的方向， Av 应由 A 点指向相的末端， Av ， v相 ， 0v 三者构成一个三角形。当 v相 取不同值时， Av 亦 随之变化。当 Av ， v相 相互垂直时，可知 Av 取得最小值。根据图 3.59 三角形相似的关系，可得 0 Av PC a v PB b   ，可得 A 船最小速度为 0 A v av b  ，C 选项正确。以地面为参照物， A 船的运动方向 为最小速度 Av 的方向，该方向与 DB 交于 F 点，因此 A 船应以 PF 方向运动。本题正确选项为 C。 例 5 (上海第 30 届大同杯初赛)如图 3.60 所示，实验室内有一 宽度 12cmd  的跑道。假设有一连串半径 5cmr  的机器人在跑 道上沿一直线鱼贯驶过，速度均为 2cm / sv  ，相邻机器人中心之 间的距离为 26cm 。某智能机器人(不考虑大小)用最小的速度沿一 直线匀速安全穿越此跑道(不与任何机器人相撞)的时间为( )。 A． 6s B．12s C．14.4s D．16.9s 分析与解 以圆形机器人为参照物，则智能机器人按照如图 3.61 所示的路径 AB (与前后两个圆形机器人相切)穿越跑道所用速度可 以取得最小值。设智能机器人相对于圆形机器人的速度为 v相 ，v相 的 方向即为 AB 方向，则智能机器人的速度与 v相 垂直时，智能机器人 速度取最小值 minv 。 minv ， v相 ， v 围成一个直角三角形，如图 3.61 所示。由相似三角形关系，可得 12 13 v v 相 ，解得 24 cm / s13v 相 ，又 5 13 d AB  ，可得 156 cm5AB  ， 因此最短时间 min 16.9sABt v   相 。本题正确选项为 D。 例 6 (上海第 29 届大同杯初赛)轮船以恒定速度沿直线航行，由于风速的影响，轮船旗杆上的 服役旗飘动的方向与轮船航行过程中所沿的直线之间往往会存在一个夹角。若船速为 v ，夹角为 60 ； 若船速为 2v (航向不变)，夹角为30 ，假设风速的大小和方向始终保持不变，则风速的大小可能为 ( )。 A．v B． 1 2 v C． 3 2 v D． 7 2 v 分析与解 旗子飘动的方向，实际是以船为参照物，风对船的相对速度方向。本题存在两种可 能。 (1)如图 3.62(a)所示，船速为 v 时，旗子飘动方向与航速夹角 60 朝船的斜后方，即此时风对船 的相对速度 1v 的方向与船速夹角 60斜向后方，当船速为 2v 时旗子飘动方向与航速夹角30 朝船的 斜后方，即此时风对船的相对速度 2v 方向与船速夹角30 斜向后方，根据如图 3.62(a)所示速度三角 形，结合几何关系可得风速 v v风 。 (2)如图 3.62(b)所示，船速为 v 时，旗子飘动方向与航速夹角 60 朝船的斜前方，即此时风对船 的相对速度 60 方向与船速夹角 60 斜向前方，当船速为 2v 时旗子飘动方向与航速夹角 2v 朝船的 斜后方，即此时风对船的相对速度 2v 方向与船速夹角30 斜向后方，根据如图 3.62(b)所示速度三角 形，结合几何关系可得风速 7 2v v风 。本题正确选项为 AD。 例 7 下雨时，雨滴均匀竖直下落，某人在雨中前进同样的路程，第一次步行，第二次跑步前 进，问：此人头顶和身体侧面哪一次淋雨较多？ 分析与解 针对题述问题，假设如下：雨滴下落速度 1v ，方向竖直向下，空中单位体积内雨滴 数为 N ，人头顶面积为 1s ，人身体侧面(迎着雨的一面)的面积为 2s ，人前进的速度为 2v ，前进路程 为l 。下面分析 2v 对头顶和身体侧面淋雨多少的影响。 将人视为如图 3.63 所示的长方体，当人以速度 2v 前进时，以人为 参照物，雨滴是倾斜着下落的，雨滴相对于人的速度记为 v相 ，v相 与竖 直方向的夹角 满足 2 1 tan v v   。人以速度 2v 前进路程l 时，淋雨时间 2 lt v  。以人为参照物，人头顶有效的淋雨面积为垂直于 v相 的投影面 积 1 coss  ，因此头顶总的淋雨量为 1 1 cosQ v t s N  相 Q，由于 1cosv v 相 ，将 2 lt v  代入，可 得 1 1 1 2 v s lNQ v  ，可见， 2v 越大，人头部淋雨越少。人身体侧面有效淋雨面积为 2s sin ，因此侧面 总的淋雨量为 2 2 sinQ v t s N  相 ，将 2 lt v  代入并考虑到 2 sinv v  相 ，得 2 2Q ls N ，可见，身 体侧面的淋雨量与前进速度 2v 无关。 三、合运动与分运动，速度的分解 物体在做某种运动时，有时根据需要，我们可以将物体的运动视为两个运 动的合成，例如沿与水平方向成 37 夹角斜向上飞行的飞机，其速度大小为 50m / sv  ，则1s 内物体前进 50m 。1s 内物体沿水平方向前进 40m ，竖直 向上升高了30m 。因此我们可以说，飞机同时参与了两个分运动：水平方向 速度为 1 40m / sv  的匀速直线运动和竖直方向速度为 2v  30m / s 的匀速直线运动。其中飞机的速 度v 通常叫做合速度 1v 和 2v 叫做它的分速度，如图 3.64 所示。合速度与分速度满足平行四边形定则， 即以分速度为邻边画一个平行四边形，则两邻边所夹的对角线就是合速度。当然，图 3.64 所示的平 行四边形恰为矩形，这仅是一种特殊情况。 例 8 降落伞在下落一定时间以后的运动是匀速的。设无风时某跳伞员着地的速度是 5m / s 。 现有正东风，风速大小是 4m / s ，跳伞员将以多大的速度着地？ 分析与解 无风时，跳伞员在下落过程，由于空气阻力的作用，最终会匀速运动。当有正东风 时，运动员最终的运动可以视为竖直向下的和水平向西的匀速直线运动的合成，由 于风速水平，运动员竖直向下的运动仍与无风时相同，而水平方向的分运动速度与 风速相同。如图3.65所示，则落地速度 2 24 5 m / s 41m / sv    ，速度与竖直 方向夹角 满足 tan 0.8  ，斜向下偏西。 物理竞赛试题中，有一类求解杆交点速度的问题——相交杆交点移动速度问题， 下面通过例题给出这类问题的解答。 所谓“相交杆”，即两个细杆交于一点，当其中一杆运动或者两杆均运动时，两杆的交点也可 能会随之而移动。这里之所以说两杆交点是“可能”会移动，是因为有时候杆移动，交点未必移动。 例如，图 3.66(a)所示的两个细杆 AB ，CD 交于 M 点，若 AB 杆沿着 AB 所在直线方向运动，则交 点 M 的位置不改变，同理，若CD 杆沿着CD 所在直线的方向运动，两杆交点 M 位置亦不会改变。 可见，某一杆运动时，沿着自身所在直线方向的速度不会引起交点的移动。当某一杆运动速度不沿 着自身所在直线方向时，我们可以把它的速度分解为沿着自身所在直线方向和沿着对方所在直线方 向的分速度，若对方静止，则沿着对方所在直线方向的分速度，即为交点的移动速度。例如，如图 3.66(b)所示， AB 杆的速度为 ABv ，CD 杆静止，则可以用下列方向求得交点 M 的移动速度：将 AB 杆的速度 ABv 分解为沿着 AB 方向的分速度 1v 和沿着 CD 方向的分速度 2v ，则 2v 即为交点移动的分速度。若 AB 杆运动的同时， CD 杆也具有速度 CDv ，则我们也要把CD 杆的速度 CDv 分解为沿着 AB 方向 的分速度 1v 和沿着 CD 方向的分速度 2v ，于是交点 M 的移动速度即为 2v 与 1v 的合速度。 例 9 (上海第 30 届大同杯初赛)如图 3.67 所示，在同一平面上的 AC ， BD 两杆分别以相同的 转动周期绕 A ，B 两轴顺时针匀速转动，当两杆转动到如图所示的位置时， 60CAB DBA    ， 此时两杆交点 M 的速度为 1v 。若 BD 杆变为逆时针匀速转动，不改变两杆的转动周期，当两杆恰好 也转动到如图所示的位置时，两杆交点 M 的速度为 2v 。则关于 1v 和 2v 关系的判断正确的是( )。 A．大小相等，方向不同 B．大小不等，方向相同 C．大小、方向都相同 D．大小、方向都不同 分析与解 当 AC ， BD 两杆分别绕 A ， B 两轴顺时针匀速转动时，如图3.68所示， AC 杆上 和 BD 杆上的 M 点转动的速度均为 v L ，方向垂直于 AC 杆，将其分解为 沿 BD 杆和沿 AC 杆的两个分速度，因为(假设 BD 杆不动)沿 AC 杆的速度不 引 起 交 点 的 变 化 ， 所 以 只 考 虑 沿 BD 杆 的 速 度 分 量 ， 该 分 量 大 小 为 2 3 cos30 3BD L Lv    。同理，把 BD 杆上 M 点转动的速度 v 分解为沿 BD 杆 及 沿 AC 杆 方 向 的 分 速 度 ， 只 考 虑 沿 AC 杆 的 速 度 分 量 ， 则 2 3 cos30 3AC L Lv    。 ACv ， BDv 两速度夹角为120 ，两者合成后即为 此时 M 的速度大小 1 1 2 3: 3AC BD Lv v v v    ，方向水平向右。 当 AC 杆绕 A 轴顺时针匀速转动， BD 杆绕 B 轴逆时针匀速转动时，同样可求得 M 的速度大 小为 2 2v L ，方向竖直向下。本题正确选项为 D。 练习题 1．一船往返于甲、乙两码头之间，船在静水中的速度为 0v ，水速为 1v ，且 0 1v v ，则船往返 一次的平均速度为( )。 A． 0 1 2 v v B． 0 1v v C． 2 2 0 1 0 v v v  D． 0 1 0 1 2v v v v 2．(上海第 25 届大同杯初赛)小轿车匀速行驶在公路上，坐在副驾驶位置的小青观察到轿车速度 盘的指针始终在100km / h 位置处，在超越相邻车道上同向匀速行驶的另一辆普通轿车的过程中， 小青发现该轿车通过自己的时间恰好为1s ，则该轿车的车速范围为( )。 A．15 ~ 20m / s B． 20 ~ 25m / s C． 25 ~ 30m / s D．30 ~ 35m / s 3．(上海第 27 届大同杯初赛)匀速前进的队伍长为 40m ，通信员以恒定速度从队尾走到队首， 然后保持速度大小不变再回到队尾，此时队伍走过的路程为30m 。则通信员走过的路程为( )。 A． 70m B．80m C．90m D．100m 4．(上海第20届大同杯初赛)小明乘坐索道到山上游玩，每隔1min 能遇见6部缆车，已知索道单 程距离为 2160m ，缆车的速度保持为1.2m / s ，则整个索道上的缆车总数为( )。 A．150 部 B．180 部 C．210 部 D．240 部 5．某商场的自动扶梯在 0.5min 内，可以把站在扶梯上的顾客送到二楼。如果扶梯不动，人走 上去需要1.5min ，那么，当人沿着开动的自动扶梯走上去时，需要的时间为( )。 A． 2min B．1min C． 0.375min D． 0.5min 6．(上海第20届大同杯初赛)由于受到水平方向风力的影响，使得原先竖直下落的雨滴斜向下方 匀速下落，则( )。 A．风速越大，雨滴下落时间会越短 B．风速越大，雨滴下落时间会越长 C．风速越大，雨滴着地速度会越大 D．风速越大，雨滴着地速度会越小 7．(上海第23届大同杯初赛)某人骑车向正东方向行驶，看到插在车上的小旗向正南方向飘动， 假设风速保持不变，骑车人沿正南方向行驶时，小旗的飘动方向不可能是( )。 A．正东方向 B．正北方向 C．东偏南方向 D．东偏北方向 8．(上海第22届大同杯初赛)轿车以5m / s 的速度匀速行驶，车前窗倾斜角为37 ，车前窗和车 顶部面积相同，雨滴竖直落下的速度为 2.5m / s ，则车窗和车顶部承受的雨量之比为( )。 A．4：1 B．3：1 C．2：1 D．1：1 9．(上海第 22 届大同杯初赛)如图 3.69 所示，某一实验室内 有一宽度为 d 的跑道，假设有一连串玩具车沿着同一直线以相同 的速度v 鱼贯驶过，玩具车的宽度为b ，前、后两车间的间距为 a 。 某智能机器人用最小的速度沿一直线匀速安全穿过此跑道，则智 能机器人要穿越跑道的时间为( )。 A． ad bv B． 2 2d a b av  C． 2 2d a b bv  D．  2 2d a b abv  10．(上海第 21 届大同杯初赛)长度为300m 的油轮在大海中匀速直线行驶，小汽艇从油轮的船 尾匀速驶向船头再返回船尾，速度始终保持为 90km / h ，所用时间为 37.5s ，则油轮的速度为 ________ km / h 。 11．如图3.70所示，两根细直硬杆 a ，b 分别沿与各自垂直的方向以 1v ， 2v 的速率运动，并保 持两杆始终垂直。此时两杆交点O 的运动速度大小 v ________。 12．(上海第 23 届大同杯初赛)如图 3.71 所示， B ，C 两点相距 60m ，C ， A 两点相距80m ， AC 与 BC 相互垂直。甲以 2m / s 的速度由 B 点向 C 点运动，乙以 4m / s 的速度同时由C 点向 A 点 运动。经过________s ，甲、乙之间的距离最近；经过________s ，甲、乙所处位置与C 点构成的三 角形和 ABC△ 可能相似。 13．(上海第 21 届大同杯复赛)以速度 v 竖直下落的雨滴，落在水平匀速行驶的汽车驾驶室的挡 风玻璃和顶棚上。驾驶室的挡风玻璃和水平顶棚均可视为平面，且面积都是 S ；挡风玻璃和水平面 成53 角，如图 3.72 所示。当司机观察到雨点垂直打在挡风玻璃上时，汽车行驶的速度为________； 落在挡风玻璃和顶棚上的雨水量之比为________。 14．(上海第 20 届大同杯复赛)如图 3.73 所示，在竖直平面内，长为1m的直 杆 AB 的 A 端紧靠在竖直的墙面上， B 端可以沿水平地面运动，现使 B 端匀速 向右运动，从 AB 杆与竖直墙面的夹角为30 时开始，到 AB 杆与竖直墙面的夹 角为 60 时结束，此过程中直杆 AB 的中点 O 经过的路程为________ m (精确到 0.01m )， A 端运动的速度大小________(选填“增大“不变”或“减小”)。 参考答案 1．C。设两地间距离为s，则船顺水航行时的速度为 s ，用时 0 1v v ，逆水航行时的速度为 0 1v v ， 用时 2 0 1 st v v   ，则往返一次的平均速度为 2 2 0 1 1 2 0 2 v vsv t t v   。 2．B。小轿车的长度大约为 3m ，小青所坐轿车的速度 0 100km / h 27.8m / sv   ，以小青所 坐轿车为参照物，则相邻车道轿车的相对速度大小为 3m / ssv t  相 相 ，因此该车的速度为 27.8m / s 3m / s 24.8m / s  ，选项 B 正确。 3．C。设通信员速度为 1v ，队伍速度为 2v ，以队伍为参照物，通信员从队尾走到队首过程中的 相对速度为 1 2v v ，通信员从队首回到队尾过程中的相对速度为 1 2v v ，设队伍长为 l ，则通信员 来回的时间 t 可表示为 1 2 2 1 2 1 2 1 2 2v ll lt v v v v v v      ，此时间内队伍前进距离 1 2 2 2 2 2 1 2 2v v ls v t v v    ， 代入数据可得 1 23v v ，因此通信员通过的路程为 1 23 90ms s  ，本题正确选项为 C。 4．B。小明相对于迎面而来的缆车的速度 2 2.4m / sv v 相 车 ，小明每隔1min 能遇见 6 部缆 车，则每10s 遇见一次缆车，因此缆车的间距为 2.4m / s 10s 24ms    ，所以，一条索道上的缆 车数为 2160 9024 s s   ，由于是双索道，因此缆车总数为 180 部，选项 B 正确。 5．B。设扶梯长为 L ，人步行速度为 1v ，电梯运行速度为 2v ，则扶梯不动人走上去用时 1 1 Lt v  ， 人站在扶梯上被电梯送上楼用时 2 2 Lt v  ，人沿着开动的自动扶梯走上用时 3t  1 2 L v v 。比较上述 三个式子可得 3 1 2 1 1 1 t t t   ，因此 3 0.375mint  。选项 B 正确。 6．C。有风时，雨滴参与了两个运动：水平方向和竖直向下速度为 v雨 的匀速运 动，雨滴实际的运动可以视为这两个分运动的合成，由于风速水平，运动员竖直向下 的运动仍与无风时相同，因此下落时间和风速无关，而水平方向的分运动速度最终会 与风速 v风 相同。如图 3.74 所示，落地速度 2 2v v v 风 雨 ，可见风速越大，落地速度 越大。选项 C 正确。 7．B。当车速 v车 向东时，小旗向正南方向飘动，说明此时风相对于车的速度是正南方向，但 是风对车的速度大小未知。画出如图 3.75 所示三个可能的风对车的相对速度 1V ， 2V ， 3V ，与之对 应的风对地面的速度 1v ， 2v ， 3v 亦可画出。当车速 v车 向正南方向时，由于风对地面的速度有多种 可能，风对车的相对速度亦有多种可能。如图 3.76 所示，若风对地面的速度分别为 1v ， 2v ， 3v ，则 对应的风对车的速度分别为 1u ， 2u ， 3u ，即旗子的飘动方向可能为 1u 所指的东偏北方向、 2u 所指 的正东方向、 3u 所指的东偏南方向，因此本题正确选项为 B。 8．C。本题有两种解答： (1)以车为参照物，则雨水参与了两个分运动：水平方向 速度为 v车 的匀速直线运动和竖直方向速度为 v雨 的匀速直线 运动。将车窗的面积沿着两个分运动投影，投影面积分别为 1s 2s ， 如 图 3.77 所 示 ， 则 1 sin37 0.6ss s   ， 2 cos37 0.8ss s   。投影面承受的雨量与投影面面积和垂 直于投影面的雨水的速度的乘积成正比，且车窗承受雨量等于投影面 1s ， 2s 承受雨量之和。因此， 车窗和车顶部承受的雨量之比 1 21 2 5 0.6 2.5 0.8 22.5 v s v sQ s s Q v s s      雨车 雨 (2)同样以车为参照物，画出 v车 ，v雨 以及雨对车的速度 v相 的三角形关系图如图 3.78 所示，设 v相 与水平方向夹角为 ，则 2 2 2 2 5 5= 5 2.5 m / s m / s2v v v   雨相 车 5sin 5 v v   雨 相 ， 2 5cos 5 v v   车 相 以车为参照物时相当于车不动，雨以 v相 的速度沿着图 3.78 所示的虚线落到车上。由于车窗和车 顶部承受的雨量与它们垂直于 v相 方向的投影面积有关，求出它们投影面积 1 sins s  37  ， 2 sin37s s 因此承受雨量之比  11 2 2 sin 37 sin v sQ Q v s    相 相 考虑到辅助角公式  sin 37 sin37 cos cos37 sin       有  1 2 2 5 50.6 0.8sin 37 sin37 cos cos37 sin 5 5 2sin sin 5 5 Q Q                综上所述，本题正确选项为 C。 9．D。以玩具车为参照物，智能机器人若要以最小速度穿过此跑道，智能机器人相对于玩具车 的运动路线应如图3.79所示的虚线 AB ，即智能机器人的相对速 度 v相 方向为 AB 方向，画出速度三角形可知，只有当智能机器 人对地速度与 v相 垂直时，方能使其取得最小速度 minv 。结合几 何关系，可得 AB 之间的距离 ABs 满足 2 2 ABs a b d b  ，得 2 2 AB d a bs b  。又 v v 相 2 2 a a b   ， 得 2 2 avv a b  相 ，因此  2 2 min AB d a bst v abv    相 ，选项D正确。 10．54。设油轮长为 L ，油轮速度为 2v ，小汽艇速度为 1v ， 1 90km / h 25m / sv   ，取油轮 为参照物，则汽艇从油轮的船尾匀速驶向船头的相对速度为 1 2v v ，从船头再返回船尾的相对速度 为 1 2v v ，则往返所用时间 1 2 1 2 L Lt v v v v    ，代入数据可解得。 11． 2 2 1 2v v 。两杆的交点沿 a 杆前进的速度为 2v ，沿b 杆前进的速度为 1v ，交点的实际速度 为 1v ， 2v 的矢量和，即 2 2 1 2v v v  。 12．6；12 或 90 11 。求解甲、乙之间的距离何时最近，我们可以以乙为参照物(即认为乙静止不动)， 如图 3.80 所示，将甲、乙的速度 v甲，v乙 的起点画在 B 点，则由 v乙 末端指向 v甲末端的有向线段 v相 即表示甲相对于乙运动的速度，由勾股定理知 2 2v v v  甲 乙相 2 5m / s ，过 B 点作 BD 平行于 v相 ， 则直线 BD 即为甲相对于乙运动的轨迹。过C 点作CE 垂直于 BD ，则CE 的长度即为甲、乙之间的 最短距离。由几何关系知 CEB△ 与 v甲 ， v乙 ， v相 围成的三角形相似，可得 vBE BC v  甲 相 ，解得 12 5mBE  ，因此经过 1 12 5 s 2 5 BEt v   相 6s 时甲、乙相距最近。 设经过 2t 时间，甲、乙两物体分别运动至 1B ， 1C 位置，如图 3.81 所示，则 1 2BB v t 甲 ， 1 2CC v t 乙 ， 1 2BCB C l v t  甲 ，若此时 1 1B CC△ 与 BCA△ 相似，则根据对应边成比例，有下列两种可能的比例 式成立： 1 1B C CC BC CA  或 1 1B C CC CA BC  ，即有 2 2BC BC CA l v t v t l l  甲 乙 或 2 2BC CA BC l v t v t l l  甲 乙 ，代入数据可解得 2 12st  或 2 90 s11t  。 13． 4 3 v ，5：4。略，可参考练习题 8 的两种解法。 14．0.262，增大。如图 3.82(a)所示，设墙角为点 C ，则 ACB△ 为直角三角形， CO 为斜边上 的中线，因此 0.5mCO  ，在杆移动过程中，CO 长度不变，O 点运动轨迹为以C 点为圆心、以 0.5m 为半径的 OO 。易得 OO 所对的圆心角为30 ，因此 OO 的长度为 30 2 0.5m 0.262m360s     。 如图 3.82(b)所示，由于 AB 杆长度不变，因此杆端 A ， B 的速度 Av ， Bv 沿杆方向的分速度等大， 设杆与竖直墙夹角为 ，则有 cos sinA Bv v  ，解得 tanA Bv v  ，由于 Bv 不变， 逐渐增大， 因此 Av 逐渐增大。