人教版九年级上册数学同步课件-第21章-一元二次方程复习课件 22页

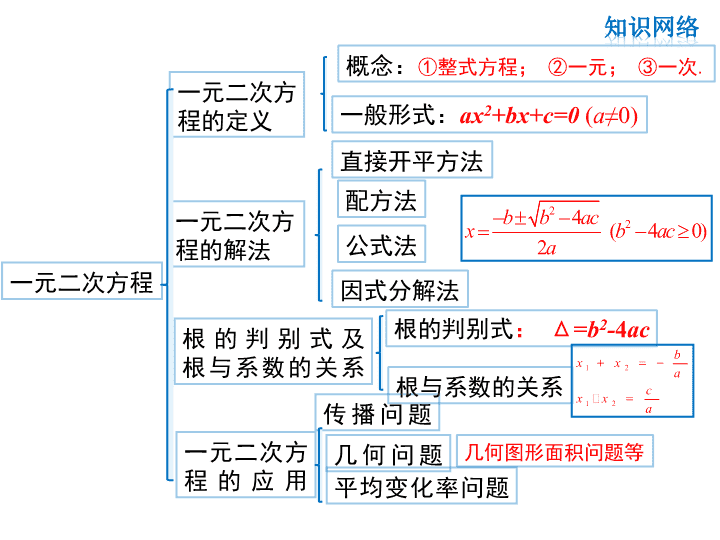
第二十一章 一元二次方程 复习课 一元二次方程 一元二次方 程的定义 概念：①整式方程； ②一元； ③一次. 一般形式：ax2+bx+c=0 (a≠0) 一元二次方 程的解法 直接开平方法 配方法 公式法 2 24 ( 4 0)2 b b acx b aca      因式分解法 根 的 判 别 式 及 根与系数的关系 根的判别式： Δ=b2-4ac 根与系数的关系 1 2 1 2 bx x a cx x a     一元二次方 程 的 应 用 传 播 问 题 平均变化率问题 几何图形面积问题等几 何 问 题 若关于x的方程(m-1)x2+mx-1=0是一元二次方程，则m的取 值范围是（ ） A. m≠1 B. m=1 C. m≥1 D. m≠0 解析 本题考查了一元二次方程的定义，即方程中必须保证有 二次项（二次项系数不为0），因此它的系数m-1≠0,即m≠1,故 选A. A 练习1： 方程5x2-x-3=x2-3+x的二次项系数是 ，一次项 系数是 ，常数项是 . 4 -2 0 一元二次方程的定义1 例1 解析 根据一元二次方程根的定义可知将x=0代入原方程一定 会使方程左右两边相等，故只要把x=0代入就可以得到以m为 未知数的方程m2-1=0，解得m=±1的值.这里应填-1.这种题的 解题方法我们称之为“有根必代”. 若关于x的一元二次方程（m-1)x2+x+m2-1=0有一个根为0, 则m= . 易错提示 求出m值有两个1和-1,由于原方程是一元二次方程， 所以1不符合，应引起注意. -1 练习2 一元二次方程x2+px-2=0的一个根为2，则p的值 为 .-1 一元二次方程的根的应用2 例2 【易错提示】(1)配方法的前提是二次项系数是1；（a-b)2与 （a+b)2 要准确区分；（2）求三角形的周长，不能盲目地将三边 长相加起来，而应养成检验三边长能否成三角形的好习惯 解析 (1)配方法的关键是配上一次项系数一半的平方； （2）先求出方程x2﹣13x+36=0的两根，再根据三角形的三边关 系定理，得到符合题意的边，进而求得三角形周长． 一元二次方程的解法 (1)用配方法解方程x2-2x-5=0时，原方程应变为（ ） A. (x-1)2=6 B.(x+2)2=9 C. (x+1)2=6 D.(x-2)2=9 (2) (易错题）三角形两边长分别为3和6，第三边的长是方程x2 ﹣13x+36=0的根，则该三角形的周长为（　） 　A．13 B． 15 C．18 D．13或18 A A 3 例3 练习3: 菱形ABCD的一条对角线长为6，边AB的长是方程x2- 7x+12=0的一个根，则菱形ABCD的周长为（ ） A. 16 B. 12 C. 16或12 D. 24 A 练习4： 用公式法和配方法分别解方程：x2-4x-1=0 （要求写出必要解题步骤）. 1 -4 -1 .a b c，公 式 ： ，法    2 4 1 .x x移 得配 法 项： ，方      22 - 4 = -4 -4 1 -1 = 2 0 0 .b a c      2 -4 2 04 2 5 .2 2 1 b b a cx a 方 程 有 两 个 不 相 等 的 实 数 根        1 22 5 , 2 5 .x x    2 2 24 2 1 2 .x x配 方 , 得       22 5x   2 = 5x由 此 可 得 ，  1 22 5 , 2 5 .x x    一元二次方程的根的判别式的应用 已知关于x的一元二次方程x2-3m=4x有两个不相等的实数 根，则m的取值范围是（ ） A. B. m<2 C. m ≥0 D. m<04 3m   A 易错提示 应用根的判别式之前务必将方程化为一般形式，这 样能帮助我们正确确定a,b,c的值. 知识点复习 >0 方程有两个不相等的实数根； =0 方程有两个相等的实数根； <0 方程没有实数根. Δ Δ Δ 解析 根据方程根的情况可知，此方程的根的判别式 >0,即 42-4×1×（-3m)=16+12m>0,解得 ,故选A.4 3m   Δ 4 例4 练习5： 下列所给方程中，没有实数根的是（ ） A. x2+x=0 B. 5x2-4x-1=0 C.3x2-4x+1=0 D. 4x2-5x+2=0 练习6：（开放题）若关于x的一元二次方程x2-x+m=0有两个不 相等的实数根，则m的值可能是　　（写出一个即可）． D 0 一元二次方程的根与系数的关系 已知一元二次方程x2－4x－3＝0的两根为m，n，则m2－ mn＋n2＝ ．25 解析 根据根与系数的关系可知，m+n=4,mn=-3. m2－mn＋n2 ＝m2+n2-mn=(m+n)2-3mn=42-3 ×(-3)=25.故填25. 【重要变形】 2 2 2 1 2 1 2 1 2( ) 2 ;x x x x x x   ① 2 2 1 2 1 2 1 2( ) ( ) 4x x x x x x   ② 1 2 1 2 1 2 1 1 x x x x x x    ③ 练习7: 已知方程2x2+4x-3=0的两根分别为x1和x2,则x12+x22的 值等于（ ） A. 7 B. -2 C. D. 3 2 3 2  A 5 例5 一元二次方程的应用 某机械公司经销一种零件，已知这种零件的成本为每 件20元，调查发现当销售价为24元，平均每天能售出32件， 而当销售价每上涨2元，平均每天就少售出4件. (1)若公司每天的销售价为x元，则每天的销售量为多少？ （2）如果物价部门规定这种零件的销售价不得高于每件28 元，该公司想要每天获得150元的销售利润，销售价应当为 多少元？ 市场销售问题 6 例6 解析 本题为销售中的利润问题，其基本本数量关系用表析分如 下：设公司每天的销售价为x元. 单件利润 销售量（件） 每星期利润（元） 正常销售 涨价销售 4 32 x-20 32-2(x-24) 150 其等量关系是：总利润=单件利润×销售量. 解：（1）32-(x-24) ×2=80-2x; （2）由题意可得(x-20)(80-2x)=150. 解得 x1=25, x2=35. 由题意x≤28, ∴x=25,即售价应当为25元. 【易错提示】销售量在正常销售的基础上进行减少.要注意验根. 128 菜农小王种植的某种蔬菜，计划以每千克5元的价格对外批 发销售.由于部分菜农盲目扩大种植，造成该种蔬菜滞销.小王为 了加快销售，减少损失，对价格经过两次下调后，以每千克3.2元 的价格对外批发销售.求平均每次下调的百分率是多少？ 解：设平均每次下调的百分率是x，根据题意得 5（1-x)2=3.2 解得 x1=1.8 (舍去）, x2=0.2=20%. 答：平均每次下调的百分率是20%. 平均变化率问题 例7 几何问题 如图1，在宽为20米，长为32米的矩形地面上修筑同样宽的 道路（图中阴影部分），余下的部分种上草坪．要使草坪的面 积为540平方米，求道路的宽. 图1 解析 本题利用图形的变换—— 平移，把零散的图形面积集中化， 再建立方程并求解. 例8 解：设道路宽为x米，由平移得到图2，则宽为(20-x)米，长为 （32-x)米，列方程得 （20-x)(32-x)=540， 整理得 x2-52x+100=0. 解得 x1=50(舍去），x2=2. 答：道路宽为2米. 图2 图1 方法归纳 解决有关面积问题时，除了对所学图形面积公式熟悉外， 还要会将不规则图形分割或组合成规则图形，并找出各部分图形面 积之间的关系，再列方程求解. （注意：这里的横坚斜小路的的宽度都相等） 平移转化 练习6： (易错题）要在一块长52米，宽48米的矩形绿地上， 修建同样宽的两条互相垂直的甬路，下面分别是小亮和小颖的 设计方案. 52 48x x图① 小亮设计的方案如图①所 示，甬面宽度均为xm,剩 下四块绿地面种共2300m2. 小颖设计的方案如图②所示， BC=HE=xm,AB∥CD,HG∥ EF,AB ⊥EF, ∠1=60 °. x x G F H E A D (1 B C 图② 52 48 解:(1)根据小亮的设计方案列方程，得（52-x)(48-x)=2300. 解得x1=2,x2=98(不合题意，舍去）. 答：小亮设计方案中甬路的宽度为2m； (2)在图2中作AI⊥CD,HJ⊥EF,垂足分别是为I,J. ∵AB ∥CD, ∴四边形ADCB是平行四边形. 由（1）得x=2, ∴AD=BC=HE=2m. 在Rt △ADI中， ∠ADC=∠1=60 °， AD=2m, ∴AI= m,同理HJ= m. ∴小颖设计方案中四块绿地的总面 积=52 ×48-2 ×52-2×48+ =2299（m2). 3 3 2( 3) x x G F H E A D (1 B C 图② 52 48 J I 一元二次 方 程 一 元 二 次 方 程 的 定 义 二次项系数是含字母系 数切记不要忽略a ≠0. 一 元 二 次 方 程 的 解 法 用自己最熟练的方法 就 是 最 好 的 方 法 . 一元二次方 程 的 应 用 传播问题，平均变化率 问题，几何面积问题， 数字问题，握手问题与 球赛问题必须熟练掌握. 1.要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据 场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比 赛组织者应邀请x个队参赛，则x满足的关系式为（　） A．x（x+1）=28 B．x（x﹣1）=28 C．x（x+1）=28 D．x（x﹣1）=28 2.一元二次方程x2﹣x﹣2=0的解是（　　） A．x1=1，x2=2 B．x1=1，x2=﹣2 C．x1=﹣1，x2=﹣2 D．x1=﹣1，x2=2 B D 4.为了宣传环保，小明写了一篇倡议书，决定用微博转发的方 式传播，他设计了如下的传播规则：将倡议书发表在自己的 微博上，再邀请n个好友转发倡议书，每个好友转发倡议书之 后，又邀请n个互不相同的好友转发倡议书，依此类推，已知 经过两轮传播后，共有111人参与了传播活动，则n= . 3.若一元二次方程ax2=b（ab＞0）的两个根分别是m+1与2m﹣ 4，则 =　　．b a 4 10 5. 2014年，某市某楼盘以每平方米4000元的均价对外销售．因为楼 盘滞销，房地产开发商为了加快资金周转，决定进行降价促销，经 过连续两年下调后，2016年的均价为每平方米3240元． （1）求平均每年下调的百分率； （2）假设2017年的均价仍然下调相同的百分率，李老师准备购买 一套100平方米的住房，他持有现金10万元，可以在银行贷款20万 元，李老师的愿望能否实现（房价每平方米按照均价计算）？ 解：（1）设平均每年下调的百分率为x,根据题意得 4000（1-x)2=3240 解得 x1= 0.1=10%; x2=1.9(舍去）； （2）购房所需资金=100 ×3240 ×（1-10%）=291600元 =29.16万元<30万元.所以李老师的愿望能实现.