中考数学复习冲刺专项训练精讲：角相交线与平行线教学课件（初三数学章节复习课件） 13页

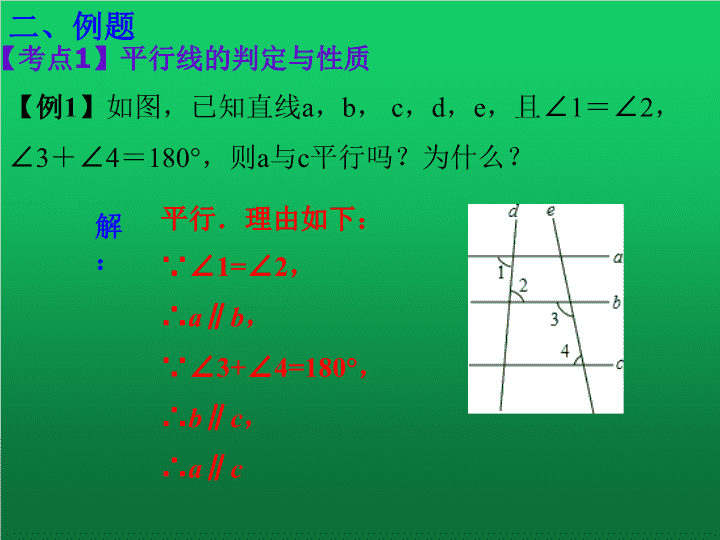
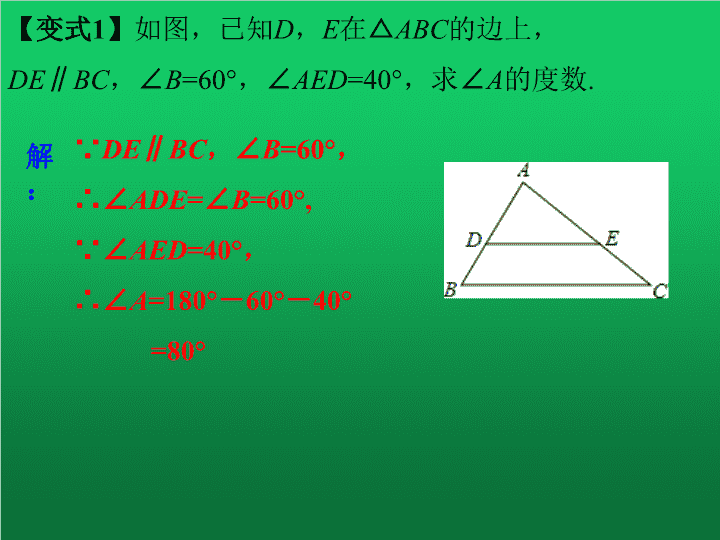
第四章 三角形 角、相交线与平行线 中考数学复习冲刺专项训练精讲 【例1】如图，已知直线a，b， c，d，e，且∠1＝∠2， ∠3＋∠4＝180°，则a与c平行吗？为什么？ 【考点1】平行线的判定与性质 二、例题 平行．理由如下： ∵∠1=∠2， ∴a∥b， ∵∠3+∠4=180°， ∴b∥c， ∴a∥c 解： 【变式1】如图，已知D，E在△ABC的边上， DE∥BC，∠B=60°，∠AED=40°，求∠A的度数. 解：∵DE∥BC，∠B=60°， ∴∠ADE=∠B=60°, ∵∠AED=40°， ∴∠A=180°－60°－40° =80° 【考点2】余角、补角、平角的定义，平行线的性质 【例2】如图，直线a∥b，点B在直线b上，且 AB⊥BC，∠1=55°，求∠2的度数． 解：∵AB⊥BC， ∴∠ABC=90°， ∴∠1+∠3=90°， ∵∠1=55°， ∴∠3=35°， ∵a∥b， ∴∠2=∠3=35° 【变式2】如图，直线AB，CD被直线EF所截，EF交AB于 点O，AB∥CD，∠BOF的 平分线交CD于点G．若∠EOB= 40°，求∠OGC的度数. 解： ∵∠ EOB =40° ，∠EOB+∠BOF=180° ∴∠BOF=140° ， 又∵∠BOF的 平分线交CD于点G， ∴∠BOG = ， ∵ AB∥CD ， ∴∠OGC=∠BOG =70°. 1 70 2 BOF   【考点3】角平分线的定义，平行线的判定 【例3】如图， B，A，D三点共线，AE平分∠DAC， ∠DAC=1200,∠C=60°.求证：AE∥BC. 解： ∵AE平分∠DAC, ∠DAC=120°, ∴∠CAE= , 又∵∠C=60°, ∴∠C= ∠CAE , ∴AE∥BC. 1 60 2 DAC   【变式3】如图，EF∥BC，直线EF经过点A，AC 平分∠BAF，∠B=80°．求∠C的度数． 解：∵EF∥BC，∠B=80°, ∴∠BAF=180°－∠B=100°， ∵AC平分∠BAF， ∴∠CAF= ∠BAF=50°， ∵EF∥BC， ∴∠C=∠CAF=50°． 1 2 A组 1.如图直线l1//l2，AB⊥CD，∠1=34°，那么∠2的度数是 . 三、过关训练 3.如图，下列条件中：（1）∠B＋∠BCD＝180°；（2）∠1＝ ∠2；（3）∠3＝∠4；（4）∠B＝∠5，一定能判定AB∥CD的条 件有 (填写正确的序号)． 56 ° 39 ° （1），（3），（4） 第3题 2.如图，直线a∥b，则∠A的度数是__________ . 4.如图， AC⊥BC于点C，AB∥CD，∠BAC＝65°， 求∠BCD度数． 解：∵AB∥CD， ∠BAC＝65°， ∴∠ECA=∠BAC＝65°， ∵AC⊥BC，∴∠ACB=90°， ∴∠BCD =180°-90°-65°=25° 5.如图， CD平分∠ACB， DE∥AC，∠1＝30°， 求∠2的度数. 解：∵CD平分∠ACB，∠1＝30°， ∴∠ACB=2∠1＝60°， ∵DE∥AC， ∴∠2=∠ACB ＝60° 6.如图，在△ABC中，∠DBC，∠BCE的平分线相交 于点O，过O作DE∥BC，若BD＋EC＝5，则DE等于 多少？ B组 解： ∵∠DBC、∠BCE的平分线相交于点O ， ∴∠DBO=∠OBC, ∠ECO=∠OCB, ∵ DE∥BC ， ∴∠DOB=∠OBC , ∠EOC=∠OCB, ∴∠DBO=∠DOB , ∠ECO=∠EOC, ∴DB=DO , EO=CE, ∵ BD+EC=5 , ∴DE=DO+EO=DB+EC=5 7.如图，在△ABC中，AB＝BC＝12cm，∠ABC＝80°，BD是 ∠ABC的平分线，DE∥BC． (1)　求∠EDB的度数； (2)　求DE的长． 解： （1）∵AB＝BC，∠ABC＝80°， BD是∠ABC的平分线， ∴∠A=∠C＝50°，∠ABD=∠CBD＝40°， ∵DE∥BC, ∴∠EDB=∠CBD＝40°. （2）由（1）知，∠ADE=∠C＝50°, ∴∠A=∠ADE＝50°, ∠EBD=∠EDB＝40°， ∴AE=DE, DE=EB， ∴AE=DE=EB，DE= AB=6 cm 1 2 C组 8.将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE 交DE于点F． （1）求证：CF∥AB； （2）求∠DFC的度数． 解： （1）∵CF平分∠DCE， ∴∠1=∠2= ∠DCE， ∵∠DCE=90°， ∴∠1=45°， ∵∠3=45°， ∴∠1=∠3， ∴AB∥CF； （2）∵∠D=30°，∠1=45°， ∴∠DFC=180°-30°-45°=105°． 1 2