中考数学二轮精品练习：函数的应用 4页

‎ ‎ 函数的应用 班级 姓名 学号 ‎ 一、知识目标 ‎1.能根据实际问题中的变量之间的关系，确定函数关系式,解决实际问题.‎ ‎2.能主动从表格或图象中获取有用信息,用一次函数或反比例函数解决问题.‎ 二、典型例题 ‎1.如图,一束光线从y轴上点A(0，2)出发，经过x轴上点C反射后经过点B(6，6)，则光线从点A到点B所经过的路程是 ( )‎ A.10 B．8 C.6 D.4‎ ‎2.若反比例函数 图象上有一点P(a,b) 且PA⊥x轴于A, S△PAO=3,则k=_______.‎ 反比例函数解析式为:_________________.‎ ‎3.如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象( 分别是正比例函数图象和一次函数图象).根据图象解答下列问题:‎ ‎(1)请分别求出表示轮船和快艇行驶过程的函数解析式 ‎(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?‎ ‎(3)问快艇出发多长时间赶上轮船? ‎ 分析:由已知条件可设两条直线分别为y=k1x(k1≠0)或y=k2x+b(k2≠0),然后根据图象给出的点的坐标,利用“待定系数法”可确定(1)中的两条直线;(2)由图可得轮船8h行160km,快艇4h行160km,分别求其速度;(3)根据追及问题中“快者路程- 相距路程=慢者路程”可求解.‎ 点评:本题主要通过一次函数图象与坐标轴的交点的意义来解决实际问题,因此弄清交点的意义是关键,然后用待定系数法求函数解析式.‎ 三、课堂练习:‎ ‎1．拖拉机开始工作时,油箱中有油40L,如果每小时耗油5L, 那么工作时,油箱中的余油量Q(L)与工作时间t(h)的函数关系用图象可表示为( )‎ ‎ ‎ ‎2．在某一段电路中,保持电压不变,则电流强度I与电阻R 之间的函数关系的图象大致是( )‎ ‎3. 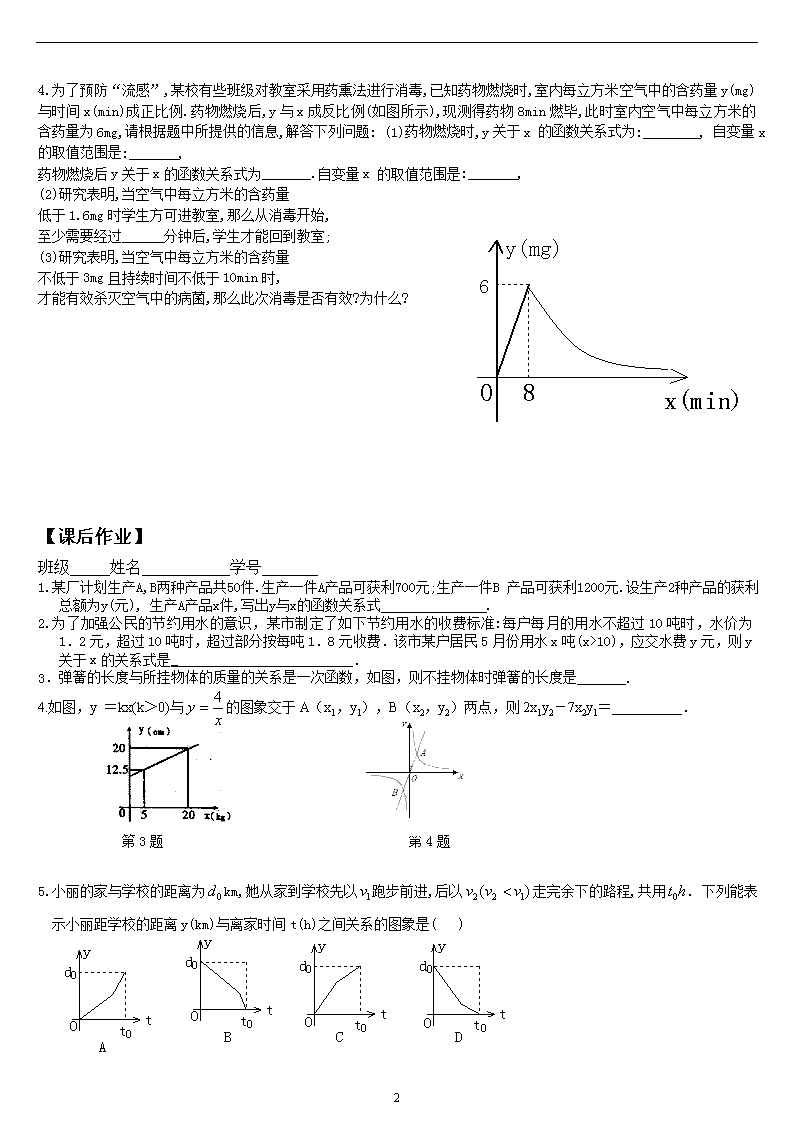如图,声音在空气中的传播速度y（m/s)(简称为音速）是气温x(°c)的一次函数，下表列出了一组不同气温时的音速 ‎（１）求y与x之间的函数关系式 ‎（２）气温x＝20(°c)时，某人看到烟花燃 放５s后才听到音响，那么此人与燃放烟花的地方相距多远?‎ 4‎ ‎ ‎ ‎4.为了预防“流感”,某校有些班级对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题: (1)药物燃烧时,y关于x 的函数关系式为:________, 自变量x 的取值范围是:_______,‎ 药物燃烧后y关于x的函数关系式为_______.自变量x 的取值范围是:_______,‎ ‎(2)研究表明,当空气中每立方米的含药量 低于1.6mg时学生方可进教室,那么从消毒开始,‎ 至少需要经过______分钟后,学生才能回到教室;‎ ‎(3)研究表明,当空气中每立方米的含药量 不低于3mg且持续时间不低于10min时,‎ 才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?‎ ‎【课后作业】‎ 班级 姓名 学号 ‎ ‎1.某厂计划生产A,B两种产品共50件.生产一件A产品可获利700元;生产一件B 产品可获利1200元.设生产2种产品的获利总额为y(元), 生产A产品x件,写出y与x的函数关系式 . 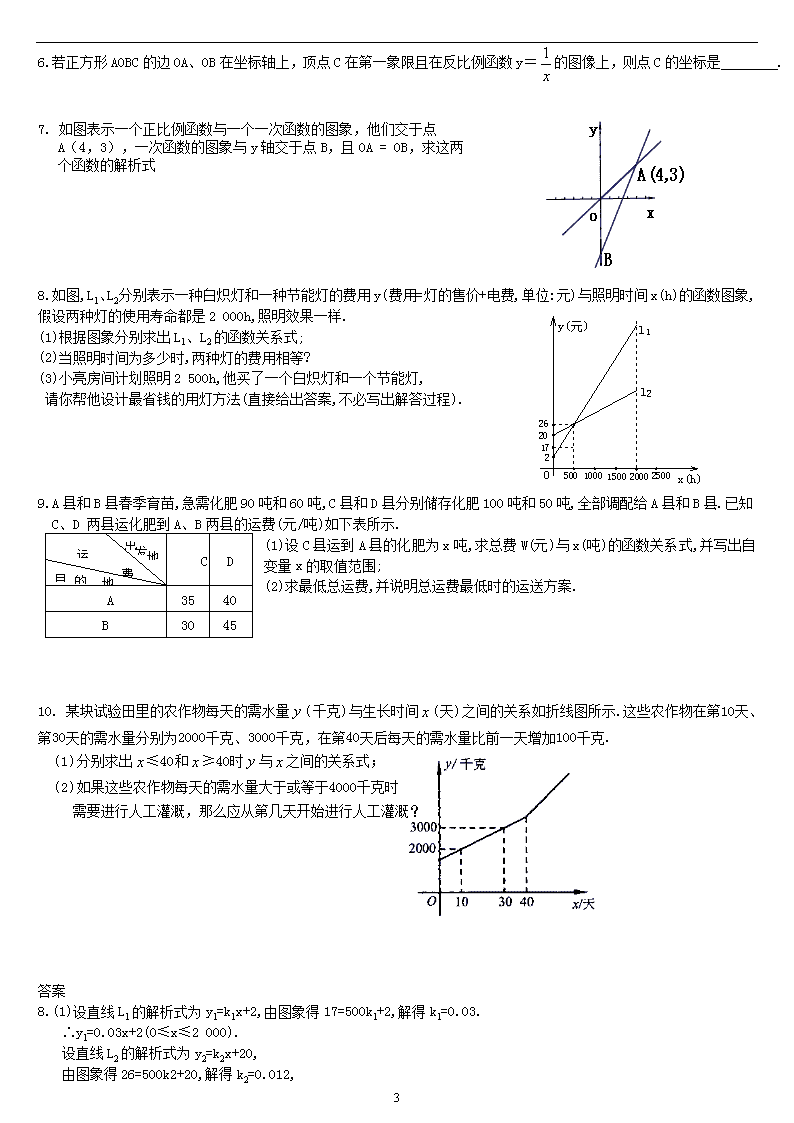‎ ‎2.为了加强公民的节约用水的意识，某市制定了如下节约用水的收费标准:每户每月的用水不超过10吨时，水价为1．2元，超过10吨时，超过部分按每吨1．8元收费．该市某户居民5月份用水x吨(x>10)，应交水费y元，则y关于x的关系式是_ ．‎ ‎3．弹簧的长度与所挂物体的质量的关系是一次函数，如图，则不挂物体时弹簧的长度是 .‎ ‎18　‎ ‎4.如图，y ＝kx(k＞0)与的图象交于A（x1，y1），B（x2，y2）两点，则2x1y2－7x2y1＝__________．‎ ‎ ‎ 第3题 第4题 ‎ ‎5.小丽的家与学校的距离为km,她从家到学校先以跑步前进,后以走完余下的路程,共用. 下列能表示小丽距学校的距离y(km)与离家时间t(h)之间关系的图象是( )‎ 4‎ ‎ ‎ ‎6.若正方形AOBC的边OA、OB在坐标轴上，顶点C在第一象限且在反比例函数y＝的图像上，则点C的坐标是 .‎ ‎7. 如图表示一个正比例函数与一个一次函数的图象，他们交于点 A（4，3），一次函数的图象与y轴交于点B，且OA = OB，求这两 个函数的解析式 ‎8. 如图,L1、L2 分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,假设两种灯的使用寿命都是2 000h,照明效果一样.‎ ‎(1)根据图象分别求出L1、L2的函数关系式;‎ ‎(2)当照明时间为多少时,两种灯的费用相等?‎ ‎(3)小亮房间计划照明2 500h,他买了一个白炽灯和一个节能灯,‎ ‎ 请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).‎ ‎9. A县和B县春季育苗,急需化肥90吨和60吨, C县和D县分别储存化肥100吨和50吨,全部调配给A县和B县.已知C、D 两县运化肥到A、B两县的运费(元/吨)如下表所示.‎ 出 发 地 运 费 目 的 地 C D ‎ ‎ A ‎35‎ ‎40‎ B ‎30‎ ‎45‎ ‎(1)设C县运到A县的化肥为x吨,求总费W(元)与x(吨)的函数关系式,并写出自变量x的取值范围;‎ ‎(2)求最低总运费,并说明总运费最低时的运送方案. ‎ ‎10. 某块试验田里的农作物每天的需水量(千克)与生长时间(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克，在第40天后每天的需水量比前一天增加100千克.‎ ‎(1)分别求出≤40和≥40时与之间的关系式；‎ ‎(2)如果这些农作物每天的需水量大于或等于4000千克时 需要进行人工灌溉，那么应从第几天开始进行人工灌溉？‎ 答案 ‎8.(1)设直线L1的解析式为y1=k1x+2,由图象得17=500k1+2,解得k1=0.03.‎ ‎∴y1=0.03x+2(0≤x≤2 000). ‎ 设直线L2的解析式为y2=k2x+20,‎ 由图象得26=500k2+20,解得k2=0.012, ‎ 4‎ ‎ ‎ y=0.012x+20(0≤x≤2 000).‎ ‎(2)当y1=y2时,两种灯的费用相等.‎ ‎0.03x+2=0.012x+20,解得x=1 000.‎ ‎∴当照明时间为1 000小时时,两种灯的费用相等.‎ ‎(3)节能灯使用2 000小时,白炽灯使用500小时.‎ ‎9.(1)由C县运往A县的化肥为x吨,则C县运往B县的化肥为(100-x)吨,D 县运往A县的化肥为(90-x)吨,D县运往B县的化肥为(x-40)吨.‎ 依题意W=35x+40(90-x)+30(100-x)+45(x-40)=10x+4 800,40≤x≤90.‎ ‎(2)∵W随着x的减小而减少,‎ 当x=40时,W最小=10×40+4 800=5 200(元).‎ 运费最低时,x=40,故100-x=60,90-x=50,x-40=0.‎ 运送方案为C县的100吨化肥40吨运往　A县,60吨运往B县,D县的50 吨的化肥全部运往A县.‎ 4‎